3D tree modeling algorithm
Автор: Pyataev A.S.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4 т.19, 2018 года.
Бесплатный доступ
Nowadays tree modeling algorithms are used in different fields of activity: from computer games to the plantation forest management. Tree modeling algorithm parameters can depend on different factors: it could be features of land- scape, climate or geographical location. Depending on the tasks to be solved, the detail level of the created model is chosen. Forest management tasks often do not require a high detail level, it is sufficient to construct a schematic plantation model. For computer games the creation of photorealistic models is required. The paper proposes an algorithm of 3D tree modeling which consists of the following steps: first step - building a tree framework (modeling the growth of a tree and adding new nodes), while under the framework is meant a set of three-dimensional vectors with attributive data for each vector; then building a tree and overlaying textures. The trunk and branches of the modeled tree are approximated by truncated cones, the axes of which are the vectors of the frame. The tree model constructing algorithm is iterative. Every iteration is a tree growth stage. Thus, the tree is gradually grown to the required level. The developed algorithm allows modeling trees of different state categories. The feature of the proposed algorithm is the possibility of constructing a three-dimensional tree model with any detail level. For example, for coniferous trees it is possible to built a tree up to each needle.
3d, tree modeling, growth model 3d
Короткий адрес: https://sciup.org/148321873
IDR: 148321873 | УДК: 004.932.2 | DOI: 10.31772/2587-6066-2018-19-4-598-604
Текст научной статьи 3D tree modeling algorithm
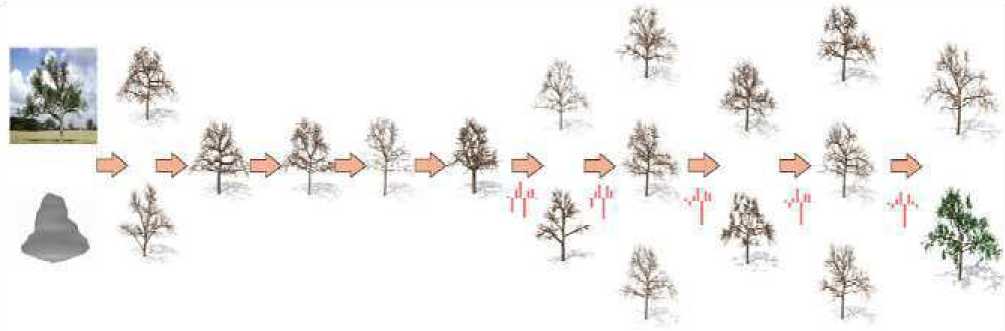
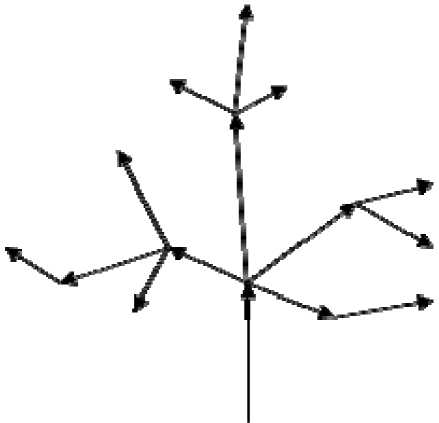
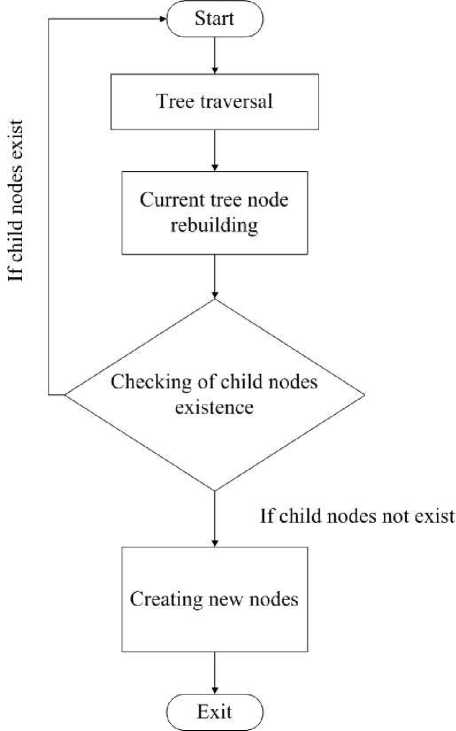
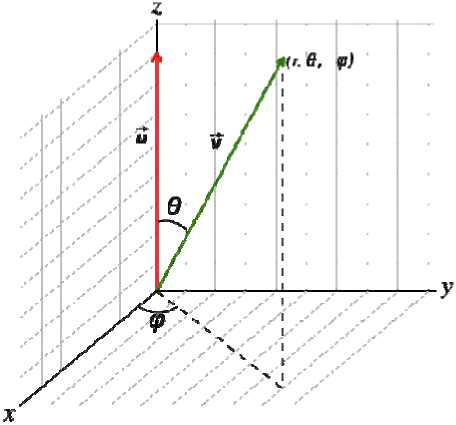
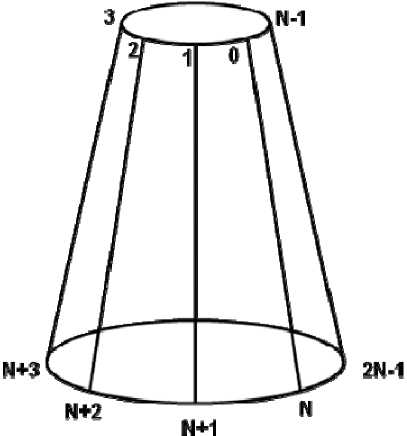
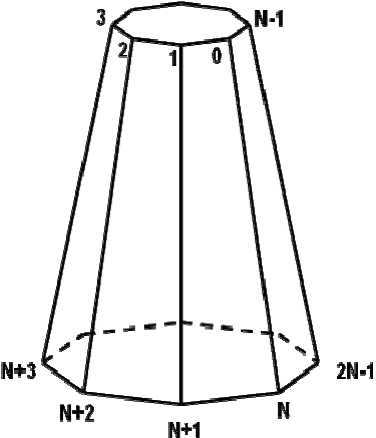
Introduction. Modclins ef teeces> is actively used in solving forecasting problems. Thus, in [1] tae norecast of forestrecoveiy aftef a lite ss bniifin [2] tSo calculation of forest scnvecal iei tire: long Олту is carrigd out, the authors [3] buiie f ferssast ob inrteic hoavest using h model of vine growth. As ten same thus:, Sie bgarnnes of the growth of Tee trgg depend not only on thy bsced, but also on the growino condition,. Thot it, when building a model of a pnrticulae tree, it t :песешгбу to et^doa onO) m:c2unt climatic featseec end tire: iniSncTbe olt the t^rrmo. eLealistic models of trees can tie invO on the dasis of data obduncd from aircraft no ng active ofitcbl systems [bS—6]_ Also, tree models ate steed i- many computer games. Thr paper [7] proposes ti growth oeodvi The f)ei)er [9, ^uggesir ide mtcracOvf wo- of modeling of а toon rvhich is dboad on the interacbon of Cih usnr wP6 thr eyclm. Ai the first stage, ihe system ccfaibr several pretending modrls frim the contouv of Cic Cen cre-atedby hoe uset. Foom tht:os mob^h^s tbc u:>er nbkais Sbl2 most ouitable trees. ftcor :sell:cihd tides ntt еПип automaticallo processed by the суПт tc anate new cac-odahe models. Atypifaleaample is shoornin ftg. 2. T h tin. Скь isskt 1:!Sai require moiielino ob dceo can be core diverse: tdmn computer cbmis:s do rnnhcHng the grov^tV oC itbds Ll claпtationo. Cteei^nding on tint pradlem to toe solcad, ono ne dttoit1m meSdv0 oC -oe mogntiag and itslcccloddetallcrecdosen|T0a-131. ^Lii algorh:hin for conshructing a tree in three-dhrnensional space. Ttie: Coemoioddl ts dcser'ded as a dlas-sical treeldke ilynlmic.■ chruhttcie of Constchction of a thlcddamicnaюnal mod^l nt the inee takcsptace bi ccccfalstfgbs: 1. The consiпtcSionor tkeireerrame: - maCetifn C'i:u dпttvth; 2. Builbiiig a Cove on ix: framcandae;aly^ngiehtures. Fgt. T :a:oicoileal-):iaeccoPtal-.llclodcl daddingcewoodns. Рис.Т Представление модели Lorix pa0oaipi-thuppcerhii1 Fes.2. Stages oftree modeling procedure Ftg.3. W:irehramptroemodel Рис.З. Каркас дерева Undec the tape smme we andsnsdanf e sec af tPree-rOmangoensl vectors with the aifrboute date for eech vector <4? Taa algonthee for cooeioneaing a trrra model is itera-iive. Eeeh itcsatton ia a stage eS icffgrowthSfig.4t. hOut, ihetceeOg nesnosllygrowut ie theeequireO level. Son nnw rade v is ecesienbyPePeciing frhmthesar-eni naPt й by an engle 9 and Oenoeeg шоипр it l)y an sngle ф (fog. 5). RtellnSenPrf coaoninate spstem ia used in Shigcase. Tae rotaties hf the custpieatf myetem Ъ>у angles 9 sna ф is obiatneg from fem compousSSen oO rotations sceona the О У sna OZ axss. The oageo nf Usui is the Sellewing: 1) tom abouanaaxts О Y iereoghan anglesf 9 ; 2) tom abouanaaxts OZ ieceoghan angles f ф. Tfr mafex oO ieSstiaf ef Uso tetgoahnate system iheeogh anjjh:s 9 sna ф has nfenoml: M (9,Ф) = Mz (Ф).Му(9) = ^ees9 ■ eegф ^шф gin9 ■ eegф> ees9 ■ gin ф eegф gin9 ■ ginф ч -ginф 0 ees9 y L,itt (9v, ф„) - пР: roltltiun anpies oh tnp new ngpe v cplsiivf te thie escant naft й. But hPn поре u , on iti tom, ii alee rotatrУ. te hfme englene ilunntinh them (9й, фu) celsiive es hfe axis OZ in hui bafa coousiank: amtem. TPey afe calculatet ley formuSss si irioniitCn:h 6em spPeri-eslcooKlUiaP; systemtoCaatesian. Fag.4. Crcagrowtlimodclmgalgoritlim Рйс.4. Алгоритм моделирования роста дерева Fig.S.Ncwnodccrcalingctagc Рис.5. Построение нового узла каркаса дерева Рис. 6. Представление конуса в X3D Thus, the oesuknag irtataeion laiatrixi will lie crleolated by the Permula: M = M (9 „, фц)• M (6 v, ф v). (2) Accordinyly, the erurOinaSesof lho new node v io the base Crrfesiha ccrrdinale syetem oan la calauloted hn the Permula: (x) ( 0 ) Tv I A ) = M. L , whoro L istho looglhoO tlee newteotnude. To viuuatize о alrolsOlmccsioaal iree model booed on Ihe constIUCled Oramnwouk, wx well uno the VRML three-Utmeosteoal image deecripteon ihwgnaae rr its dcecendant X3D [15.. A sloatgUi tiunuateo isnc is coneUuoted on the basts o)f 1Пз amme oO cads nolle. Radit sO baste - the rrtlhmoltc moao bolwooo ttie aaifa^eleru oh thn usfdnp of lho current nude uoh the netb“bor at Shir bttse. The axis cP thocone ss the vectoa oO the nude. A airaighl homceted eonr in X3D, from a mathe-mrltcrl eohit of ninw, is a aagulaa trunuatsd fsuamid ^g.6.. Scfhnpaтfmld sedeserlOed as follows: The 0 12... N - 2 TV-1 -1, (4) whoro -Iso theacoe deeariptsonepnaraSoe. The Х1 У1 Zl, yl zl Z2, -. X2 N-1 УгМ-Х Z2 V-1 . (5) The foltowOig eeunocoe oe oPejris es uoed to stлeslruct lhoi;one: 1. The cooroinesep of tiae baeas эте urlculated, lho c^oseal oO fee towrr bsee Iles at fee p 2. The angles 9 and ф for the nulf vsctrr are carcu-lrloO. 3. The coordinates oO tOia cone are recalculated toting tolo account Our soiatton mahix M (9, ф) according to the slrlomohl(1). ^iir ampniilp o1U a toas uasod on thts ags Thus, ustog tin ooio>ldcaeP apaproacr te modeling lroos, you con aiutld r irrc montl rofp uny deepeu of de-1гГ1. Frr exfmalз, fot Conclusion. The paper proposos an alnrritlrm Con con-slrucltog a tree muacV whirs le itcratioo and end itera-ltoo ss a ^teup oO tree gcowehl rags algorShas ui based no the iuioa of modalmg a Oreo bys i^s roanuat “nrowing” to lho aaeut i aaui ivaef TOr OunO ооП CoaduPal et mu- simu-lrloO troo one pprsxximateh lay 1hcncatan conat, rXo axes cP white are the framc sectors. “of varuidii'ihuia of the cooslruclou haeeeoSmleilsnзiial model nO a tree ^he language cP ttie tlo^;crip)tioil ppf t0aro-meo2nshnlbl Imesup of 3D is usou. Uowo tlis Vovckiurp ilt)pi'oablr st ts pbseibte to mouol trees wtth sny gegree of delnO aud different cate-gortosoO saae.: Fig.7.3D tree wlthtextures Рис. 7. Трехмерное дерево с наложенными текстурами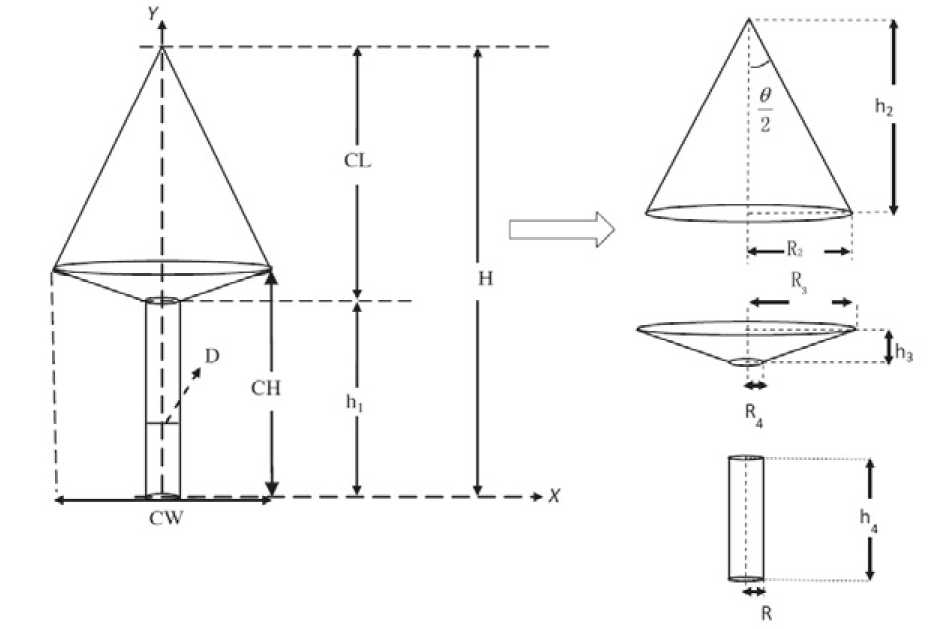

Список литературы 3D tree modeling algorithm
- Lindsay M. Grayson, Robert A. Progar, Sharon M. Hood. Predicting post-fire tree mortality for 14 conifers in the PacificNorthwest, USA: Model evaluation, development, and thresholds // Forest Ecology and Management. 2017, Vol. 399, P. 213-226.
- Christopher Thurnher, Mario Klopf, Hubert Ha- senauer. MOSES - A tree growth simulator for modelling stand response inCentral Europe // Ecological Modelling. 2017. Vol. 349. P. 58-76.
- Alberto Bressan, Michele Palladino, Wen Shen. Growth models for tree stems and vines // Journal of Differential Equations. 2017. Vol. 263. P. 2280-2316.
- Efficient Tree Modeling from Airborne LiDAR Point Clouds / Shaojun Hu [et al.] // Computers & Graphics. 2017. DOI: 10.1016/j.cag.2017.04.004
- Validation of a functional-structural tree model using terrestrial Lidar data / Robert Beyera [et al.] // Ecological Modelling. 2017. Vol. 357. P. 55-57.


