A Cluster Based Job Scheduling Algorithm for Grid Computing

Published Online November 2013 in MECS DOI: 10.5815/ijitcs.2013.12.09

Computational grid has the potential for solving large-scale scientific problems using geographically distributed and heterogeneous resources. Grid scheduling is a vital component of a computational grid infrastructure, which plays an important role in the efficient and effective execution of various kinds of scientific and engineering applications [1, 2]. A grid system is formed using many heterogeneous or homogeneous resources to deal with large-scale scientific problems. There are many issues in using grid computing. How to appropriately and efficiently assign resources to tasks, generally called job scheduling, is one of the important issues. The main purpose of job scheduling is to shorten the job completion time and enhance the system throughput. A grid scheduling system should take the various characteristics of grid applications and resources into account. In a grid environment, the resource providers and tasks are all changing constantly, so the traditional scheduling algorithms, e.g. ‘‘First Come, First Serve’’ may not be suitable for a dynamic grid system. It is very important to assign appropriate resources to tasks. Through a good scheduling method, the system can perform better and applications can avoid unnecessary delays.

When science and technology advance, the problems encountered become more complicated and need more computing power. In contrast to the traditional notion of using supercomputers, grid computing is proposed. Distributed computing supports resource sharing. Parallel computing supports computing power. Grid computing aims to harness the power of both distributed computing and parallel computing. The goal of grid computing is to aggregate idle resources on the Internet such as Central Processing Unit (CPU) cycles and storage spaces to facilitate utilization. The Search for Extra-Terrestrial Intelligence (SETI) experiment [3] is an early application of grids. The data Trans-Atlantic Grid project (TAG) [4] constructs a large-scale intercontinental grid test bed which focuses on issues of advanced networking and interoperability between these intercontinental grid domains, hence extending the capabilities of each and enhancing the worldwide program of grid development.

In implementation, Globus Toolkit [5] is an open source and a fundamental enabling technology for grid. The latest version of Globus Toolkit is Globus Toolkit 5.2.0. Grid can achieve the same level of computing power as a supercomputer does, but at a much reduced cost. Grid is like a virtual supercomputer. However, we need to consider about many conditions such as network status and resource status because the members of grid are connected by networks. Grid is also a heterogeneous system. Scheduling independent tasks on it is more complicated. In order to utilize the power of grid computing completely, we need an efficient job scheduling algorithm to assign jobs to resources. This paper focuses on the efficient job scheduling considering the average waiting time, average turnaround time, average response time and average total completion time of jobs in a grid computing.

Grid scheduling presents several challenges that make the implementation of practical systems a very difficult problem. Our research aims to design and develop Grid scheduling algorithms that makes efficient utilization of resources, maintain a high level of performance and possess a high degree of scalability.

This paper presents a dynamic cluster based job scheduling algorithm for efficient execution of user jobs. This paper also includes the comparative performance analysis of our proposed job scheduling algorithm along with other well-known job scheduling algorithms e.g.; First Come First Served (FCFS), Longest Job First (LJF), Shortest Process Next (SPN), Round Robin (RR), Proportional Local Round Robin (PLRR), Multilevel Dual Queue (MDQ). We evaluated the performance and scalability of each scheduling algorithm on a computational grid using six key performance parameters, i.e. average waiting time, average turnaround time, average response time and average total completion time in a grid computing.

The remainder of this paper is organized as follows: Section 2 gives related research. Section 3 describes the proposed cluster based hybrid scheduling algorithm. Section 4 presents the performance evaluation of grid scheduling algorithms. Conclusion is given in the final section.

• II.    Related Research

A Grid is a high performance computational system which consists of a large number of distributed and heterogeneous resources. Grid computing enables sharing, selection and aggregation of resources to solve the complex large scale problems in science, engineering and commerce. Scientific applications usually consist of numerous jobs that process and generate large datasets. Processing complex scientific applications in a Grid imposes many challenges due to the large number of jobs, file transfers and the storage needed to process them. The scheduling of jobs focuses on mapping and managing the execution of tasks on shared resources [6]. Most of the parallel jobs demand a fixed number of processors, which cannot be changed during execution [7]. Good job scheduling policies are very essential to manage Grid systems in a more efficient and productive way [8]. Grid job scheduling policies can be generally divided into space-sharing and time-sharing approaches. In timesharing policies, processors are temporally shared by jobs. In spacesharing policies, however, processors are exclusively allocated to a single job until its completion. The well-known space-sharing policies are FCFS, Shortest Job First (SJF), Shortest Remaining Time First (SRTF) and Longest Job First (LJF) approaches. The famous time- sharing scheduling policies are Round Robin (RR) and Proportional Local Round Robin Scheduling (PLRR) [9, 10, and 11]. In [9] the authors have extended the working of basic space sharing techniques like FCFS, SJF, and LJF and proposed an SJF-backfilled scheduling heuristic. First-Come, First-Served Scheduling Algorithm (FCFS) is the simplest algorithm for job scheduling. Jobs are executed according to the sequence of job submitting. The second job will be executed when the first job is done, and therefore FCFS has a serious problem called convoy effect [12]. Or The FCFS is the simplest and non-preemptive job scheduling algorithm. For this algorithm the ready queue is maintained as a FIFO queue. Each new job/process is added to the tail of the ready queue and then the algorithm dispatches processes from the head of the ready queue for execution by the CPU. A process terminates and is deleted from the system after completing its task. The next process is then selected from the head of the ready queue [10, 11].

• [20]    Proposes Grid level resource scheduling with a Job Grouping strategy in order to maximize the resource utilization and minimize the processing time of jobs. A combination of the Best Fit and RR scheduling policies is applied at the local level to achieve better performance. With RR, a fixed time quantum is given to each process that is present in the circular queue, for fair distribution of CPU times. The RR scheduling policy is extensively used for job scheduling in Grid computing [20, 21, and 22].

This paper presents a dynamic cluster based job scheduling algorithm for efficient execution of user jobs. This paper also includes the comparative performance analysis of our proposed job scheduling algorithm along with other well-known job scheduling algorithms considering the parameters like average waiting time, average turnaround time, average response time and average total completion time. The result has shown also exhibit that Our proposed scheduling algorithms (CHS) has shown the best average waiting times, average turnaround times, average response times and average total completion times compared to other job scheduling approaches.

• III.    Proposed Cluster based Hybrid Scheduling Algorithm

• 3.1    Cluster based Hybrid job Scheduling Algorithm (CHS)

• 3.2    Method of Time Quantum Calculation

In [13, 14 and 15] Shah et al proposed two scheduling algorithms- MH and MDQ. They are based on a fixed time quantum.

In this paper we propose new dynamic cluster based hybrid job scheduling algorithm namely CHS will now be described.

In this method (Fig. 1), a central node considered as Master Node plays the role of taking jobs from users and storing them in its local memory. Then, the jobs are ordered based on CPU calculating burst time, and the jobs are distributed between the clusters. Thereafter, the jobs are numbered from 1 to n for each cluster. Then, the time quantum of Cluster 1 to Cluster n is calculated in parallel. Then, the cluster with a lower quantum time is CPU allocated and executed.

According to the below relation, time quantum is calculated based on the square of CPU burst time average for Cluster 1 to Cluster n in parallel. Then, the cluster with a lower time quantum compared to other clusters is CPU allocated and executed.

Quantum cluster1 =

SQRT (Average (JCT1, JCT2, JCT3, .„, JCTi))

Quantum cluster2 =

SQRT (Average (JCTi+1, JCTi+2, JCTi+3, ..., JCTj))

Quantum cluster3 =

SQRT (Average (JCTj+1, JCTj+2, JCTj+3,^, JCTn))

In the above relation, the JCT variable represents job processing time. In this proposed method, due to the fact that we cluster the jobs and that time quantum is calculated in parallel for all clusters, hence, this method results in improved waiting time, return time, response time, and total completion time, and acts better than FCFS, RR, LJF, PLRR, and MDQ scheduling algorithms. JCT (Job CPU TIME)

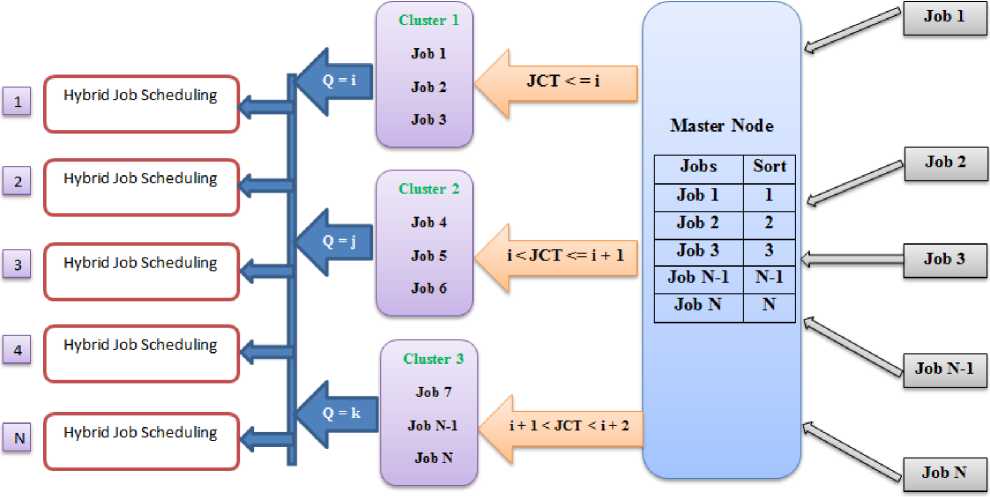
Fig. 1: Block Diagram of Cluster based Hybrid Scheduling (CHS)

• IV.    Performance Evaluation of Grid Scheduling Algorithms

  Performance metrics for the Grid scheduling algorithms are based on three factors - Average Waiting Time, Average Turnaround Time, and Average Response Time. We performed experiments for different scheduling algorithms [18]. We formed two data sets by using workload i.e. 19000 and 38000 processes. We performed an experiment by varying the number of CPUs from 8 to 128. We used ‘50’ units as the fixed time quantum for our experiment. In this section, we describe a comparative performance analysis of our proposed algorithms, i.e. CHS, with six other Grid scheduling algorithms; i.e. FCFS, LJF, SPN, RR, PLRR and MDQ.

• 4.1    Average Waiting Times Evaluation

  The Waiting Time is the time for which a process waits from its submission to completion in the local and global queues [16], [17]. Fig. 1 and Fig.2 shows that the average waiting times computed by each scheduling algorithm for each real workload trace of 19000 and 38000 processes. That the PLRR and CHS scheduling algorithms produce the shortest average waiting times as compared to the other scheduling algorithms. By increasing the number of CPUs, each algorithm shows the relative improvement in performance, except for the FCFS and MDQ algorithms. Also, the FCFS and LJF have shown the worst performance the average waiting time measures. As a result, CHS has shown the optimal average waiting times for 19000 and 38000 processes.

• 4.2    Average Turnaround Times Evaluation

  The Turnaround time of the job is defined as the time difference between the completion time and release time [16], [17]. Fig. 3 and Fig. 4 shows that the average turnaround times computed by each scheduling algorithm for each real workload trace of 19000 and 38000 processes, That the average turnaround time computed by the RR, PLRR and CHS scheduling

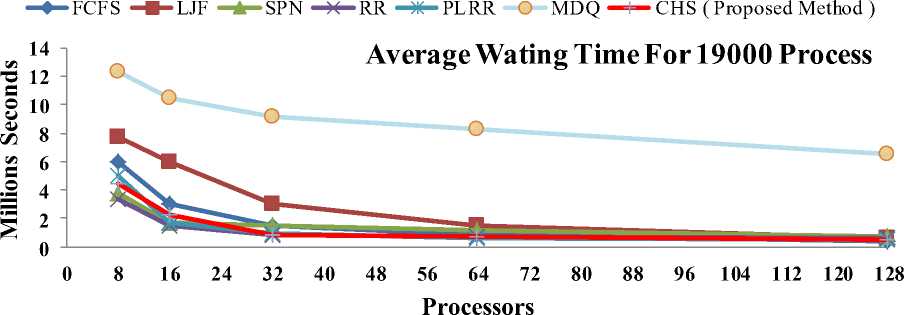
Fig. 1: Average Waiting Time Analysis for 19000 Processes

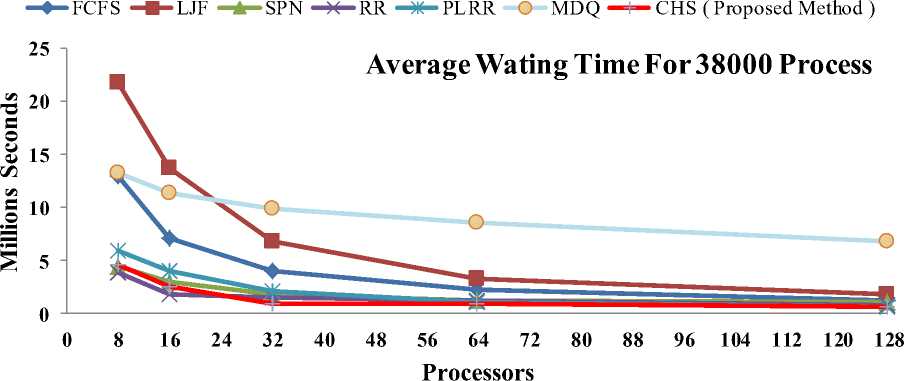
Fig. 2: Average Waiting Time Analysis for 38000 Processes

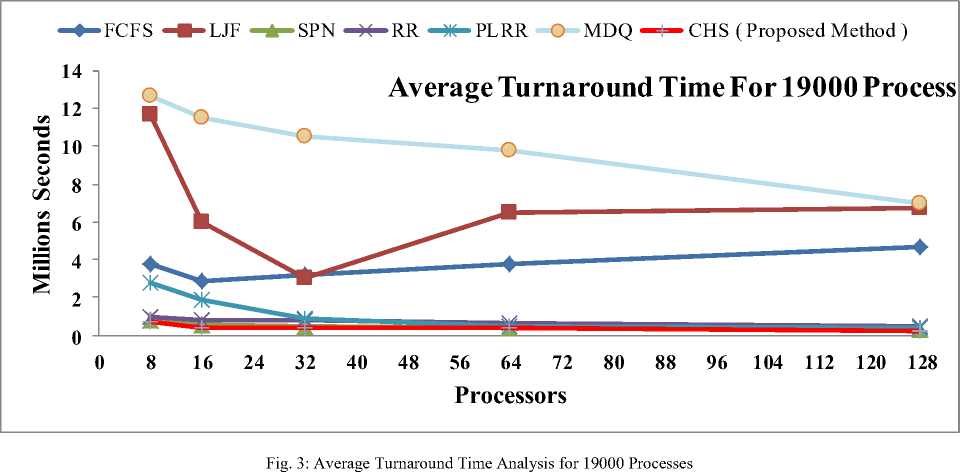
algorithms are shorter than the other Grid scheduling algorithms, Also By increasing the number of CPUs, each algorithm has an improved average turnaround time, except for the LJF and FCFS scheduling algorithm. Furthermore, it is found that FCFS, MDQ and LJF scheduling algorithms have shown the longer average turnaround time measures.

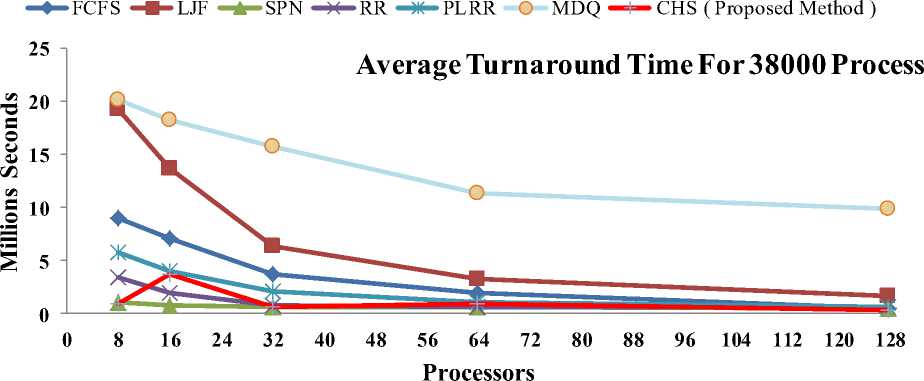
Fig. 4: Average Turnaround Time Analysis for 38000 Processes

• 4.3    Average Response Times Evaluation

  It is the amount of time taken from when a process is submitted until the first response is produced [16], [17]. Average response times for each algorithm have decreased by increasing the number of CPUs. Fig. 5 and Fig. 6 shows that the average response times computed by each scheduling algorithm for each real workload trace of 19000 and 38000 processes, The SPN, LJF and

FCFS scheduling algorithms result in poor response times as compared to the other scheduling algorithms. It also shows that MDQ and RR algorithms produces better average response time compared to other algorithms. However, FCFS, PLRR, SPN and LJF have shown the worst performance average response time measures, out of which LJF results in the longest average response times.

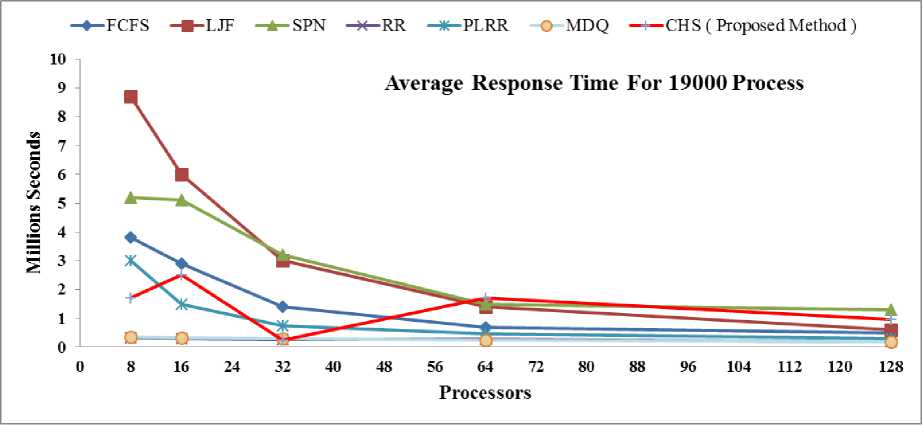
Fig. 5: Average Response Time Analysis for 19000 Processes

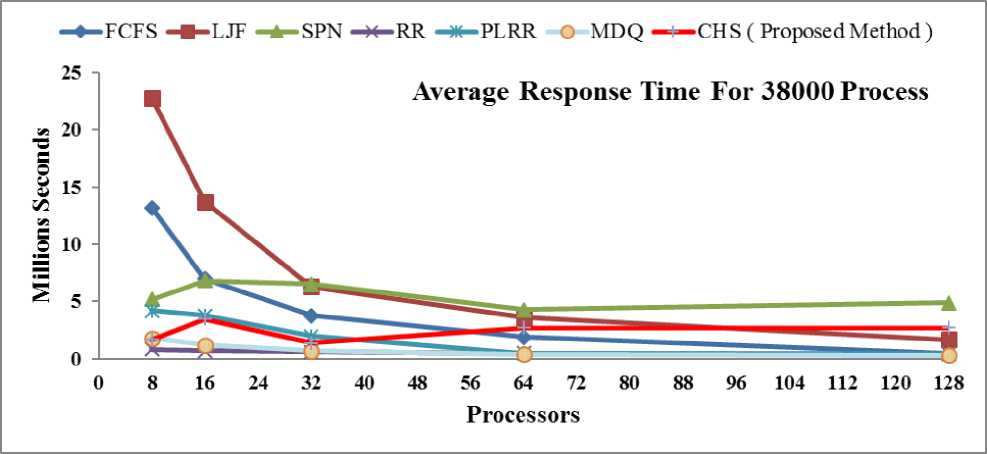
Fig. 6: Average Response Time Analysis for 38000 Processes

• 4.4    Average Total Completion Times Evaluation

Machine Completion time is defined as the time for which a machine ‘m’ will finalize the processing of the previously assigned tasks as well as of those already planned tasks for the machine [19]. Fig. 7 and Fig. 8 shows that the average total completion times computed by each scheduling algorithm for each real workload trace of 19000 and 38000 processes, That the average total completion times computed by the RR, SPN and CHS scheduling algorithms are shorter than the other Grid scheduling algorithms, it is found that FCFS, MDQ, PLRR and LJF scheduling algorithms have shown the longer average turnaround time measures.

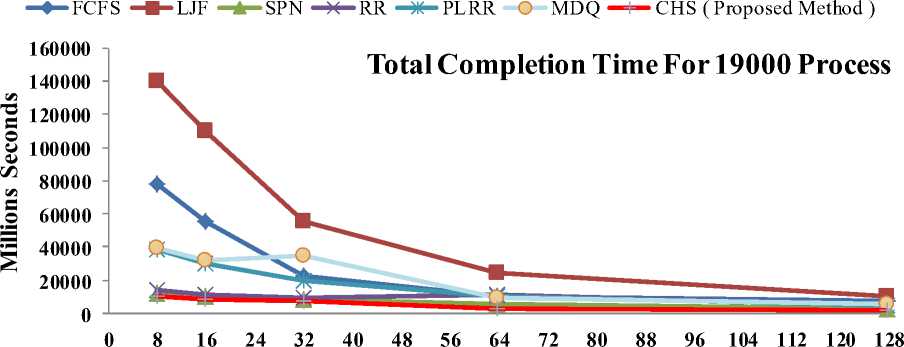
Processors

Fig. 7: Average Total Completion Time Analysis for 19000 Processes

—♦—FCFS —■- LJF    SPN    RR -*- PLRR    MDQ    CHS ( Proposed Method )

3 500000

.о 300000

^ 200000

Total Completion Time For 38000 Process

8   16  24  32  40  48  56  64  72   80  88  96  104  112  120  128

Processors

Fig. 8: Average Total Completion Time Analysis for 38000 Processes

• V.    Conclusion

In this paper, the architecture of a cluster-based scheduling framework of the Grid computing is proposed, namely CHS. We compared the performance of proposed job scheduling algorithm with other grid scheduling algorithms on a computational grid. Simulation results show that CHS has shown the optimal performance in terms of average waiting times, average turnaround times, and total completion times. Simulation results also exhibit that MDQ and RR has shown the best average response times compared to other job scheduling approaches.