A Clustering-based Offline Signature Verification System for Managing Lecture Attendance

Published Online July 2017 in MECS

Classroom attendance management involves keeping track of attendance of students in a classroom, laboratory, seminar, etc. Attendance management is important because attendance affects students’ academic performance. Moreover, in many institutions, if students do not attend a minimum number of classes for a course, they either fail the course or they are prevented from earning a regular grade in the course. Different techniques such as iris recognition [1], face recognition [2], Radio Frequency Identification [3, 4] have been used by researchers to manage attendance. This paper introduces a clustering-based signature verification technique for attendance management. Implementation of the technique uses inexpensive scanners. Moreover, capturing of attendance in the class is done offline without the need to power any devices. These two reasons make the proposed system well suited for use in developing countries.

Signatures are behavioral biometric that contain unique features that adequately identify an individual [5]. Signatures are legally acceptable means of identification and authorization of individuals. They have also been identified as the most natural and socially acceptable way of identifying an individual. Unlike physiological biometrics where direct physical contact is required, measurement of signatures is noninvasive and so reduces undesirable health implications [6, 7]. Signatures are widely used to identify individuals in different application domains such as education, legal, finance, security, and business. Signatures are unique to individuals; however, there are intrapersonal variations which occur even in signature samples of the same individual. It is therefore important to verify that signature(s) belongs to their authentic owner.

Signature verification problem, which involves verifying the identity of an individual based on the analysis of their signature, is a global issue. The task of signature verification is difficult for humans as the unique features that exist in signatures are not all visible to the human eyes. Manual signature verification also requires a lot of time to realize accurate results [8]. Therefore, an automated signature verification system is essential to enhance verification. There are two approaches to automatic signature verification systems and it is based on the method of acquisition of the signature: online and offline approaches [7]. Online signature verification systems use an electronic tablet and pen to input signatures into the system. The system captures dynamic information such as pressure, velocity, other unique features found within the signature. On the other hand, in the offline approach, signature is signed on paper and input to a system as an image, from which extracted image features are measured and analyzed [7]. Though offline signature verification systems have less accurate results due to the lack of dynamic information such as time, pressure and velocity, they are nonetheless very important since most official documents are signed offline.

Automatic signature verification has mainly utilized supervised learning, commonly classification techniques

[7, 9, 10], where features extracted from signature samples are stored in a knowledge base, and subsequent signatures supplied to the system are compared to samples in the knowledge base. Supervised learning obtains known set of input data and known responses to the data, and seeks to build a model that generates reasonable response to new data [11]. Classification is a form of supervised learning because the technique operates under supervision by being provided with the actual outcome for each of the training data (i.e., the learning of the classifier is supervised as it is told which class each training data belongs) [12]. This contrasts with unsupervised learning in which the class label of each training data to be learned are not known in advance. Clustering is a form of unsupervised learning in which no information is given about the training data. It does not rely on predefined classes and class-labeled training; rather, learning is by observation.

In this paper a new verification technique is proposed where hierarchical clustering, which groups data objects into a tree of clusters in hierarchies is used for lecture attendance management. Clustering is the process of grouping data into clusters or classes; such that objects within a cluster are similar compared to objects in other clusters [13]. Measures are used to define similarity or dissimilarity of objects in clusters. Two main types of measures are distance measures such as Minkowski metric, Euclidean distance and Manhattan distance; as well as similarity measures like Cosine Measure and Pearson Correlation Measure [14].

The main contributions of this paper are two-fold; firstly, a novel set of features (plane features) is introduced. These features which are based on the black pixel information along the signature image column were experimentally found to be representative as well as distinctive. Secondly, an unsupervised learning technique based on hierarchical clustering is used for signature verification, unlike existing works on signature verification which rely on supervised learning techniques.

The rest of the paper is organized as follows: Section II discusses related works on offline signature verification. Section III focuses on hierarchical clustering while Section IV describes automatic lecture attendance management. Section V details the proposed automatic lecture attendance management system. Experimental results are presented in Section VI and the paper is concluded in Section VII.

• II.    Related Works

From literatures, several classification concepts and techniques have been proposed and evaluated in the context of offline signature verification, some of them include: Euclidean distance classifiers [15, 16]; Bayes classifiers [17]; k-nearest neighbor [18, 19]; Hidden Markov model [8]; Support vector machine (SVM) [20 -24] and Multilayer perceptron [15, 25 - 27]. A few of the reviewed works focused on writer identification. Signature verification and writer identification are related since verification of signatures are comparable to analyses of letters [17].

Ref. [15] developed an offline verification system using pseudo dynamic features derived from Zernike moments of each segment. The Euclidean distance model was used for measuring signature similarity during the verification phase and an accuracy rate of 86% was obtained. Euclidean distance model was also used for signature verification in [16]. However, features were extracted from image cell size, image centre angle relative to the cell lower right corner and pixels normalized angle relative to the lower right. resulting in 1% error in rejecting skilled forgeries and 0.5% error in accepting genuine signatures.

Bayes classifier has been used for the offline signature verification and identification system developed in [17]. In the system, preprocessing was done using principal component analysis to make signature images rotation invariant. Gradient, Structural and Concavity (GSC) features were utilized. During the verification phase, probability distribution between same writer and different writer was taken to classify unknown samples Experiments were carried out on CEDAR database; Results showed accuracies of 78% for verification and 93% for identification.

K Nearest Neighbor classifier was used to develop an Arabic writer identification system in [18]. Major steps carried out in the system were; preprocessing to get rid of documents background, feature extraction and classification. Global features based on statistical measurements were extracted from edge hinge and grapheme of characters. The experimental dataset consisted of 20 Arabic characters from 10 individuals. Ref. [19] has also utilized k Nearest Neighbor classifier although the features were based on measurement of words, edge direction distribution and moment invariants.

Ref. [8] has used a Hidden Markov Model (HMM) classifier for offline signature verification system. The projections of signature images were obtained at different angles distributed between 0 and 360 degrees; each processed projection was taken as a feature vector. Each signature sample was modeled by a ring structured Hidden Markov Model implementing Viterbi reestimation algorithm. The system had equal error rate (EER) of 12.6%.

Support vector machines (SVM) are popular classifiers used for offline signature verification. SVM has been used in conjunction with chain code histogram features [20]; surroundedness features [10]; as well as features extracted from number of loops, normalized area, centre of gravity, centroid, vertical and horizontal profile of the signature images [26]. Similarly, SVM has been used for classification during the verification phase of other systems [23, 24].

Multilayer perceptron (MLP) was implemented for offline signature verification and recognition system in [26]. Features were derived from eccentricity, skewness, kurtosis and orientation of the signature image. Similarly, Ref. [27] used MLP to verify signatures represented using the Eigen-sign feature vector. Furthermore, Ref. [25] used MLP for English character recognition.

• III.    Hierarchical Clustering

Hierarchical clustering techniques group data objects into tree of clusters in hierarchies. There are basically two hierarchical clustering algorithms: agglomerative and divisive hierarchical clustering algorithms [22]. Agglomerative hierarchical clustering algorithms start with points as individual clusters and at each step, they merge the closest pair of clusters. In contrast, divisive hierarchical clustering algorithms start with one all-inclusive cluster and at each step split until only one cluster is left. For both algorithms, number of clusters is not user-specified. Agglomerative hierarchical clustering algorithm is known to produce better cluster quality than divisive hierarchical clustering algorithm [29].

Hierarchical clustering results are displayed graphically using tree-like diagrams called dendrograms. Dendrogram trees display clusters-sub clusters relationships as well as the order in which clusters are merged. Dendrogram trees need to be cut to attain high intra-cluster similarity and low inter-cluster similarity. However, a threshold must be defined to be used as the value for the cut-off argument. The thresholds of the links in the cluster tree can identify these divisions where the similarities between objects change abruptly. Fig. 1 shows a dendrogram of agglomerative hierarchical clustering of student signature samples. From the dendrogram, the most similar signatures are samples 3 and 6, which were first merged together, followed by 2 and 5, then lastly 4 and 1. Algorithm 1 lists the basic steps for basic agglomerative hierarchical clustering.

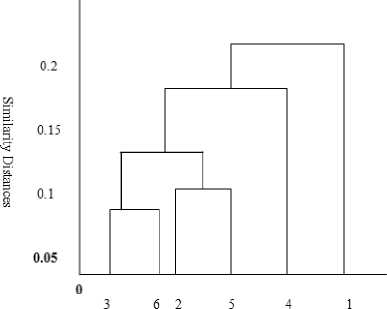
Signature samples

Fig.1. Dendrogram of hierarchical clustering

• IV.    Automatic Lecture Attendance Management

Automatic Lecture Attendance Management (ALAM) is concerned with determining the number of times each enrolled student has attended lectures for a particular course by examining signatures recorded on a lecture attendance sheet. A lecture attendance sheet is a table consisting of rows and columns. Each row contains information about one student. The first two columns store the name and registration number of students. Every other column is used to record the signatures of students that attend a particular lecture.

Step 1:

Determine the distance between each pair of points or objects using Euclidean distance

Step 2:

Iteratively group points into a binary hierarchical tree (linkage).

Single linkage for two sets of observations A and B is given as:

Min {d(x,y) :xcA, ycB}

Step 3:

Connect the closest pair of points and re-compute distance matrix

Step 4:

Cut the hierarchical tree into clusters

Algorithm 1. Basic agglomerative hierarchical clustering

On the first day of class, each student enters his/her registration number and name then signs for that day. In subsequent lectures, students simply sign on the cell that matches their row and the column for that lecture. Fig. 2 shows a sample lecture attendance sheet containing signatures for five students who enrolled for a course that was taught for ten weeks. The first student missed the fourth lecture while the third student missed the second and fourth lectures.

ALAM involves examining each cell of the attendance sheet to compute the number of lectures each student attended, given that one of four cases is possible: (i) a student was absent and no one signed for him/her (ii) a student was present and signed on the attendance sheet (iii) a student was absent but someone else signed for him/her. (iv) a student was present but forgot to sign the attendance sheet.

It is straightforward to detect the first case since the cell is left blank. The fourth case is not handled in this paper since it rarely happens. The most challenging issue in ALAM is distinguishing between the second and third cases. For every signature on the attendance sheet, it is necessary to determine if the signature is genuine, that is, if it belongs to the student whose name and registration number are on that row of the attendance sheet.

A fairly straight forward approach to ALAM is to store specimen(s) of genuine signatures for each student at the beginning of the semester. Thereafter, specimen signatures are compared to signatures on the attendance sheet to determine if they are genuine or forged. However, this paper proposes an unsupervised verification approach which eliminates the need to capture specimen signatures of students at the beginning of the semester.

• V.    Automatic Lecture Attendance Management System

In this paper lecture attendance management is formulated as an offline signature verification problem. Features are extracted from offline signature samples signed on the attendance sheet and based on the extracted features, signature(s) are verified to be genuine or forged. There are three main types of forgeries: random, simple and skilled forgeries [8, 30]. However, this work focuses on skilled forgery as students can view the genuine signature samples of all other students from the attendance sheet. The proposed lecture attendance management system accepts lecture attendance sheets containing student signatures as input. The output of the system is the estimated number of times each student attended class. Signature images are first extracted from the attendance sheet and preprocessed. Next, from each preprocessed signature image suitable features are extracted and passed to the verification module which uses hierarchical clustering algorithm. The frame work of the system is shown in Fig. 3. The next subsections discuss preprocessing, feature extraction and verification phases in detail.

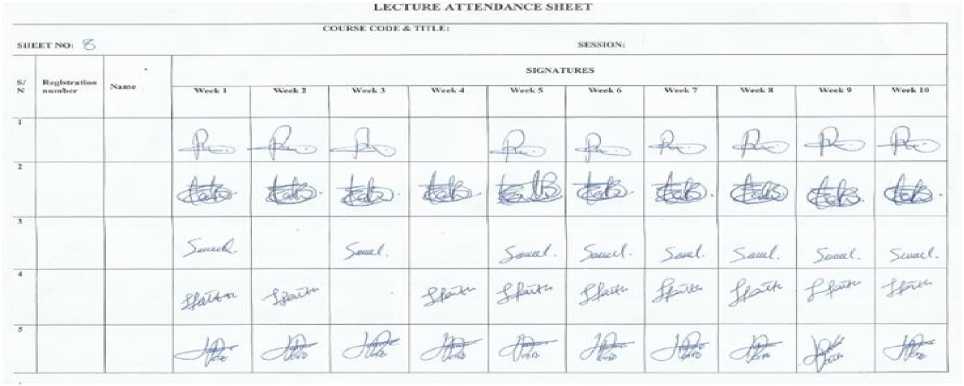
Fig.2. Lecture attendance sheet

Fig.3. Framework of Automatic Lecture Attendance Management System

• A.    Signature segmentation and preprocessing

When an attendance sheet is scanned, it results in a single image. Signature segmentation involves splitting that image into individual signature images. Segmentation is straightforward because each signature cell on the attendance sheet is a rectangle of known dimension (see Fig. 2). Preprocessing was carried out to enhance the quality of the signature images. Signature images were first converted from RGB to grayscale images after which they were binarized using Otsu’s tresholding technique in MATLAB. A threshold level of 0.9 was selected experimentally for all signatures, thus pixel values below the set threshold are considered foreground while other pixels are considered background. Binary representation of the signature images is particularly suitable as images can be represented as black and white pixels. That is, signature details are represented as black pixels and background as white pixels. Fig. 4 shows the results of the preprocessing phase.

• B.    Feature extraction

Feature extraction is a very important aspect of signature verification because the system’s efficiency, processing cost, and memory requirement are largely dependent on the feature set [10]. Also, the feature set considered should sufficiently reveal the characteristics of forged signatures such as shaky lines, discontinuity of lines, texture density [28].

In this paper, a set of plane features which consider the distribution of black pixels along each column (plane) of signatures images is proposed. This set of features measures the texture in the signature images; it can also reveal structural information of images. Fig. 5 shows black pixels along the planes. The highlighted column shows the plane being considered, the ‘+’ marks show positions of black pixels. To show common and representative characteristics of the signature, plane features were summarized using four statistical measures (Entropy, Mean, Median and Standard deviation). Equations for the statistical measures are given as follow:

(a)

(b)

(c)

Fig.4. Results of preprocessing on a student’s signature sample. (a) Unprocessed image, (b) Greyscale image, (c) Binarized image

+				+
	+		+
+		+		+
+	+		+
+

(a)

+				+
	+		+
+		+		+
+	+		+
+

(b)

+				+
	+		+
+		+		+
+	+		+
+

(c)

Fig.5. Plane count in different columns (a) plane count at column 1 = 4 (b) plane count at column 2 = 2 (c) plane count at column 5 = 2

n

Entropy , E = - £ P i x log 2 P i

s. p

Mean, M^ = -^- n

I П + 1 I

Median, M-, = l-----I th value in the sorted list of p

2 i

Standard deviation , M

^Ap.- m i )²

Where n is the width of the signature image and p is the number of black pixels in column of the signature image. Therefore, four features were extracted from the distribution of black pixels on the columns of a signature image.

• C. Ver f cat on

In this phase, the signatures in each row of the attendance sheet are examined to determine how many are genuine, that is, how many times each student actually attended lectures. The following steps are carried out during verification.

• 1)    Construct on of dendrogram:

The features of all the signatures on each row are supplied as input to the agglomerative clustering algorithm to produce a dendrogram.

• 2)    Ident f cat on of clusters:

Using a suitable similarity threshold, the different signature clusters are identified. Each point where the similarity threshold line cuts the dendrogram results in a cluster. Intuitively, each cluster represents a different individual since the clustering is based on the similarity/dissimilarity of signature features. Thus, the number of clusters identified indicates the number of individuals who signed for a given student, whereas the number of signature samples in each cluster indicates how many times the individual signed. Fig. 6 shows that using a similarity threshold of 0.17, three clusters are obtained: signature specimens 3, 6, 2 and 5 form cluster

one; only signature specimen 4 belongs to cluster two; while cluster 1 contains only signature specimen 1. This indicates that one individual signed four times, while two other individuals each signed once. It is noteworthy that the similarity threshold needs to be carefully selected. If it is too large, the system will be unable to detect forgeries since only one cluster will always emerge. On the other hand, if the threshold is too low, genuine signatures will not be detected as the system assumes that there are many impostors.

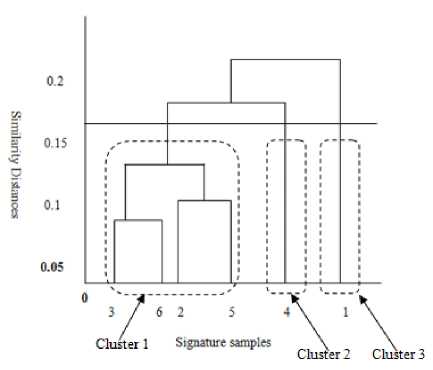
Fig.6. Determination of frequency of lecture attendance from dendrogram

3) Determ nat on of frequency of attendance:

Finally, the cluster with the highest number of signature samples is chosen as representing the genuine student, and the number of signature samples in the chosen cluster is returned as the number of lectures the student attended. Note that in real life, an overwhelming majority of students attend lectures most of the time, thus it is reasonable to assume that the individual who signs the highest number of times on a row of the attendance sheet is the genuine student. From Fig. 6, the system determines that the student attended four lectures and signed for himself/herself, but during two other lectures, two different students falsified the student’s signature.

• VI.    Experimental Results

This section discusses experiments that were used to empirically validate the proposed automatic lecture attendance management system.

• A.    Experimental setup

  The MATLAB R2010a simulation tool was used to implement the ALAM system. All experiments were carried out on a computer system having a processor speed of 2.4 GHz as well as main memory capacity of 4GB, and running the 64-bit Windows® 7 operating system. A binarization threshold level of 0.9 was selected experimentally for all signatures, thus pixel values below 0.9 were considered foreground and the values that were at least 0.9 were considered background. Agglomerative hierarchical clustering algorithm was implemented for the verification phase, and it was experimentally determined a threshold value of 2.1 was suitable for identifying the clusters in a dendrogram.

• B.    Data collection

Student signatures were collected on the lecture attendance sheets which have the following columns; Students’ registration number, students’ name and weeks in the semester. Fig. 2 shows a lecture attendance sheet for a course taken in 10 weeks. 479 signatures were collected from 50 students during a 10-week class. There were 21 blank spaces on the attendance sheets because students were sometimes absent and nobody signed for them. Of the 479 signatures on the attendance sheet, 446 were genuine signatures while the remaining 33 were forgeries because other students signed for the absent students.

• C.    Results and discussion

Fig. 7 shows how mean square error (MSE) varies with the similarity threshold. As can be observed from the figure, the optimal similarity threshold value is 2.1, which results in MSE of 0.96. Fig. 8 shows the actual and predicted frequencies of lecture attendance for 50 students which resulted in the MSE of 0.96. As previously stated in this paper, the threshold value needs to be carefully chosen. If it is too low, there will be too many clusters, and the system assumes that there are many impostors. An extremely low threshold value (such as zero) makes the system accept only one signature as genuine and all other as forgeries. On the other hand, when the threshold value is too high, there will be too few clusters and the system erroneously accepts many signatures as genuine. An extremely high threshold value treats all signatures as genuine.

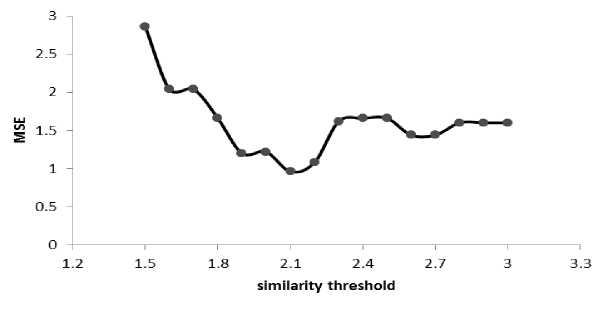
Fig.7. Relationship between similarity threshold and mean square error

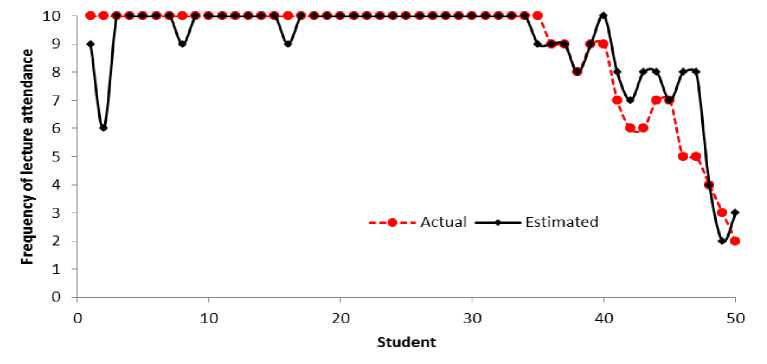
Fig.8. Predicted and actual frequencies of lecture attendance

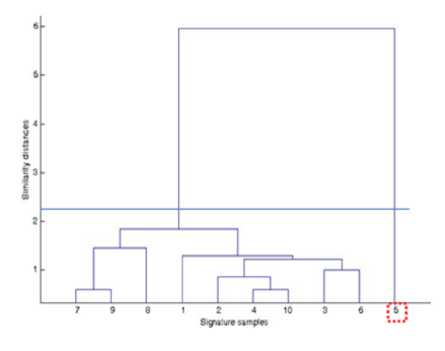
Fig. 9 shows the signatures on one row of the attendance sheet for the 36th student as well as the corresponding dendrogram obtained by clustering features of the signatures. The student attended nine out of ten lectures. However, during the fifth lecture, another student forged the student’s signature. The forged signature is enclosed in a dashed red square on Fig. 9a while the genuine signatures are enclosed in solid green squares. It can be noticed from Fig. 9b that the similarity threshold line correctly cuts the dendrogram into two clusters; the cluster on the right contains the only forged signature, while the cluster on the left contains all the genuine signatures.

(a)

(b)

Fig.9. Results for 36th student (a) signature on row of attendance sheet (b) corresponding dendrogram

1                    2         3         4         5            6         7         8         9

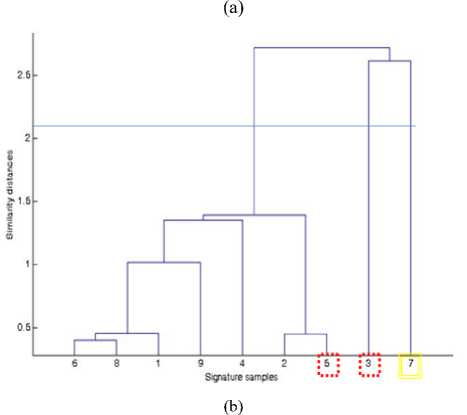
Fig.10. Results for 41th student (a) signature on row of attendance sheet (b) corresponding dendrogram

Fig. 10 shows the signatures on the row of the attendance sheet for the 43rd student along with the corresponding dendrogram. The student attended six lectures during which she signed for herself (see the solid green squares on Fig. 10a). The student missed the second lecture and no one signed for her. However, during the other three lectures which the student missed, her signature was forged. Whereas one student forged the third and fifth signatures encircled in dashed red squares on Fig. 10a, the seventh signature enclosed in a yellow square was forged by a different student. The dendrogram on Fig. 10b correctly indicates that there are three clusters, i.e., three different signatories. The cluster on the left incorrectly includes the third signature which should have fallen into the middle cluster, while the seventh signature correctly lies in the rightmost cluster. The attendance management system thus erroneously estimates the frequency of lecture attendance for the 43rd student as seven, rather than six.

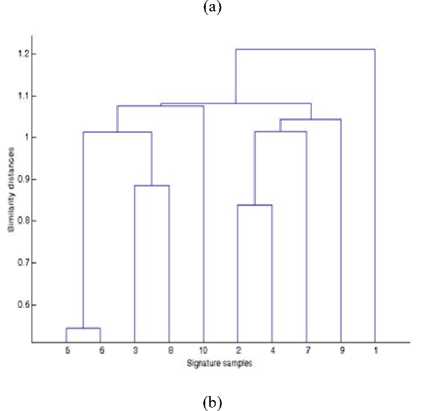
Fig.11. Results for 15th student (a) signature on row of attendance sheet (b) corresponding dendrogram

Fig. 11 shows the signatures on the row of the attendance sheet corresponding to the 15th student together with the resultant dendrogram obtained by clustering features of the signatures. The student attended all ten lectures hence all signatures on Fig. 11a are enclosed in solid green squares. The similarity threshold line is not shown in Fig. 11b because at threshold of 2.1, the threshold line should appear far above the dendrogram. Consequently, all ten signatures appear in one cluster, and the system correctly determines that the student attended all the ten lectures.

• VII.    Conclusion

Although offline signature verification has traditionally been carried out using supervised machine learning techniques, this work has shown how clustering, which is an unsupervised machine learning technique can be used to effectively verify signatures in order to manage lecture attendance. The research has shown some interesting and promising results. The work can be improved upon in three ways. (i) Experimental results may be improved if individual similarity thresholds for identifying clusters in dendrograms are determined for each student, rather than our current use of a single global threshold. (ii) This research has assumed that the largest cluster of signatures always belongs to the genuine student. Whereas this assumption is reasonable, the system would produce incorrect results in exceptional cases when an impersonator signs more frequently than the genuine student. Future works can focus on tackling this issue. (iii) Students could deliberately use signatures that are too simple (such as a single vertical stroke) so that the signatures can be easily forged whenever the students are absent. It will be interesting to devise means of identifying overly simple signatures so that they can be rejected.

Acknowledgment

The authors acknowledge their use of computing facilities belonging to the Department of Computer Science, Federal University of Technology, Minna, Nigeria. Authors are indebted to the students who gave out signatures samples for this research. Finally, the authors are grateful to the reviewers whose valuable comments have improved this manuscript.