A Comparative Analysis of Multigranular Approaches and on Topoligical Properties of Incomplete Pessimistic Multigranular Rough Fuzzy Sets

Published Online October 2012 in MECS

The introduction of the concept of rough sets as a model to capture impreciseness by Pawlak [5, 6], has been found to be a very useful tool and several applications of this model has been made so far. The basic assumption of rough set theory is that human knowledge about a universe depends upon its capability to classify these objects. Classifications of a universe and equivalence relations defined on it are known to be interchangeable notions. So, for mathematical reasons equivalence relations were considered by Pawlak to define rough sets.

A rough set is represented by a pair of crisp sets, called the lower approximation and upper approximation of the set, comprising of elements which definitely and possibly belong to it respectively with respect to the available information.

To improve the modeling capability of basic rough sets several extensions have been made in different directions. One such extension is the rough sets based upon tolerance relations instead of equivalence relations. These rough sets are sometimes called incomplete rough set models [1]. In the view of granular computing, classical rough set theory is researched by a single granulation. The basic rough set model has been extended to rough set model based on multigranulations (MGRS) in [7], where the set approximations are defined through multiple equivalence relations on the universe. Using similar concepts, that is taking multiple tolerance relations instead of multiple equivalence relations; incomplete rough set model based on multi-granulations was introduced in [8]. Several fundamental properties of these types of rough sets have been studied [7, 8, 9]. In [19], the concept of Multigranulation has been extended to the context of fuzzy sets. Another type of Multigranulation called the pessimistic Multigranulation was introduced by Qian et al [10]. The first contribution of this paper is a comparative analysis of these two types of Multigranular rough sets and the Indiscernibility relation obtained by the intersection of these equivalence relations.

There are two different ways of characterizing rough sets; the accuracy coefficient and the topological characterization introduced through the notion of types. It is noted [6] that in practical applications of rough sets we need to combine both types of information about the borderline region. Keeping this in mind, Tripathy and Mitra [13] have studied the types of rough sets by finding out the types of union and intersection of rough sets of different types. These results were extended to the context of optimistic multi granular rough sets by Tripathy et al [14], multi granular rough fuzzy set in [15] and pessimistic multi granular rough set in [18]. The second contribution of this paper is that we study the above topological properties for the pessimistic multi granular rough fuzzy sets. The results obtained are important from the point of view that we provide suitable examples wherever necessary to show that the results actually occur.

The organization of the paper is as follows. In section 2, we present the definition of related concepts to be used in the paper along with the notations. In section 3, we provide the results of this paper, which are of two types. The first type of these results provides a comparative study of the notions of optimistic Multigranulation,     pessimistic     Multigranulation, intersection of equivalence relations and union of tolerance relations. The second type of results provides topological properties of multigranular rough fuzzy sets. Here, we provided some proofs and also examples to illustrate that all possible cases after union, intersection and complementation of rough sets actually can arise. We have ended up with a conclusion of the work done in this paper in section 4, followed up by the references of papers used for the compilation of this piece of work.

elements of X, employing knowledge of R . We say that X is rough with respect to R if and only if R X ≠ RX , equivalently BN ( X ) ≠ φ . X is said to be R-definable if and only if R X = RX , or BN ( X ) = φ .

In the view of granular computing (proposed by L. A. Zadeh), an equivalence relation on the universe can be regarded as a granulation, and a partition on the universe can be regarded as a granulation space [2, 3]. For an incomplete information system, similarly, a tolerance relation on the universe can be regard as a granulation, and a cover induced by the relation can be regarded as a granulation space. Several measures in knowledge base closely associated with granular computing, such as knowledge granulation, granulation measure, information entropy and rough entropy, were discussed in [2, 3, 4]. Qian and Liang [7] put forth a rough set model based on multi-granulations (MGRS), which is established on multiple equivalence relations. In [8] this notion is extended to rough set model based on multi tolerance relations in incomplete information systems.

There are three regions for a rough set, namely, interior having elements definitely belongs to the set, boundary having elements possibly belongs to the set and exterior which is the complement of the closure of the interior. Rough Fuzzy Set is finer than rough set, in a sense that, in the former, membership values are associated with each object specifying the extent to which it belongs to a particular region of the set which is not so in the later. In rough set whether an element belongs to a particular region of the set or not is only known.

• II.    Definitions and Notations

Let U be a universe of discourse and R be an equivalence relation over U. By U/R we denote the family of all equivalence classes of R, referred to as categories or concepts of R and the equivalence class of an element x∈U is denoted by [x]R . By a knowledge base, we understand a relational system K = (U,P) , where U is as above and P is a family of equivalence relations over U. For any subset Q ( ≠ φ ) ⊆ P, the intersection of all equivalence relations in Q is denoted by IND(Q) and is called the indiscernibility relation over Q. Given any X⊆ U and R ∈ IND (Q), we associate two subsets, RX = U{Y∈U/R:Y⊆X} and RX = и{Y∈U/R:Yn X ≠ φ} , called the R-lower and R-upper approximations of X respectively. The R-boundary of X is denoted by BNR (X) and is given by BN (X) =RX -RX. The elements of R X are those elements of U, which can certainly be classified as elements of X, and the elements of R X are those elements of U, which can possibly be classified as

First, let us define below the Multi Granular Rough Fuzzy Set (MGRFS).

Definition 2.1: Let K= (U, R ) be a knowledge base, R be a family of equivalence relations on U, F(U) denotes the set of all fuzzy sets over U , X ∈ F (U) andP,Q ∈ R. The optimistic multi-granular rough fuzzy set X’s lower approximation and upper approximation in U can be defined as

∀ y ∈ U, (P+Q) (X)(y)=inf _{x ∈ [y]} X (x) ∨ inf _{x ∈ [y]} X (x)   (1)

We Г. (P^Q)(X)(y) — ((P+Q) (~X))(y)       (2)

Another kind of multi-granular rough fuzzy sets called pessimistic multi-granular rough fuzzy sets was introduced. Now, the above type of multi-granular rough fuzzy sets is known as the optimistic multirough fuzzy sets.

granular

The definition of pessimistic multi-granular rough fuzzy set (PMGRFS) is as below.

Definition 2.2: Let K= (U, R ) be a knowledge base, R be a family of equivalence relations on U, F(U) denotes the set of fuzzy sets over U, X ∈ F (U) and P,Q ∈ R. We define the pessimistic multi-granular rough fuzzy lower approximation and upper approximation of X in U as

∀ y ∈ U, (P ∗ Q) (X)(y) =inf _{x ∈ [y]} X(x) ∧ inf _{x ∈ [y]} X(x) (3)

Vj 6 и, ^QXXKy) =4(P*Q)(X)Xy)       (4)

Pessimistic Multi Granular Rough Fuzzy Set is finer than Optimistic Multi Granular Rough Fuzzy Set, in a sense that, the lower approximation of the former have elements belongs to both the equivalence classes where as the lower approximation of later have elements belongs to either of the equivalence classes. A similar argument holds true for upper approximation of both the sets too.

We state below several properties of pessimistic multi-granular rough sets from [10].

Property 2.1: Let K= (U, R) be a knowledge base, R be a family of equivalence relations, F(U) denotes the set of fuzzy sets over U, X ∈F(U) and P,Q ∈R. The following properties hold true.

(P∗Q)(X)⊆X⊆(P∗Q)(X)(5)

( P ∗ Q ) ( φ ) = φ = ( P ∗ Q )( φ ), ( P ∗ Q ) ( U ) = U = ( P ∗ Q )( U ) (6)

(P∗Q)( X)= ((P∗Q)(X))(7)

(P∗Q)(X)=PX  QX(8)

(P∗Q)(X)=PX  QX(9)

( P ∗ Q ) ( X )= ( Q ∗ P ) ( X ),( P ∗ Q )( X )=( Q ∗ P )( X ) (10)

Property 2.2: Let K= (U, R) be a knowledge base, R be a family of equivalence relations, F(U) denotes the set of fuzzy sets over U, X,Y ∈F(U) andP,Q ∈R. The following properties hold true.

(P∗Q)(X  Y)=(P∗Q)X  (P∗Q)Y(11)

(P∗Q)(X  Y)=(P∗Q)X  (P∗Q)Y(12)

(P∗Q)(X  Y) ⊇(P∗Q)X  (P∗Q)Y(13)

(P∗Q)(X  Y) ⊆ (P∗Q)X  (P∗Q)Y(14)

It is very obvious that all these properties hold true even for pessimistic rough fuzzy sets too.

Next, we define PMGRS in incomplete information systems.

Definition 2.3: An information system is a pair denoted by S = (U, A), where U is a non-empty finite set of objects, A is a non-empty finite set of attributes. For every a ∈ A , there is a mapping a : U → V , where V is called the value set of a.

If V contains a null value for at least one attribute a ∈ A , then S is called an incomplete information system. Otherwise, it is complete.

We define below incomplete information system for single granular rough set.

Definition 2.4:   Let S = (U, A) be an incomplete information system for single granular rough set where U and A denotes the universe of objects and attribute set respectively, and P ⊆ A be an attribute subset. We define a binary relation on U as follows

SIM(P) = {(u, v) ∈ U X U | ∀ a ∈ P, a(u) = a(v)

or a(u) = * or a(v) = *}.                            (15)

In fact, SIM(P) is a tolerance relation on U, the concept of a tolerance relation has a wide variety of applications in classifications [1].

It is known that SIM(P) = ^ p SIM({a}).

Let S p (u) denote the set {v ∈ U| (u, v) ∈ SIM(P)}. S (u) is the maximal set of objects which are possibly indistinguishable by P with u.

Let U/SIM(P) denote the family sets {S (u)| u ∈ U}, the classification or the knowledge induced by P. A member S (u) from U/SIM(P) will be called a tolerance class or an information granule. It should be noticed that the tolerance classes in U/ SIM(P) do not constitute a partition of U in general. They constitute a cover of U, i.e., S (u) ≠ φ for every u ∈ U, and

US. (u) = U. Wecan extend this definition to u∈U p single granular rough fuzzy set in a similar fashion.

Now we define below pessimistic multigranular lower and upper approximations of fuzzy sets in an incomplete information system. It may be noted that instead of the notations used in [13] to denote these concepts, we have used more meaningful and simpler notations.

Definition 2.5: An incomplete information system is a pair denoted by S = (U, A) where U is a non-empty set of objects, P,Q ⊆ A be two attribute subsets, and X ∈ F(U) be rough fuzzy set in U. Then we define a lower approximation and an upper approximation of X in U with respect to two tolerance relations of P and Q by the following

( P ∗ Q ) ( X ) = и{ x / SIM ( x ) ⊆ X and SIM ( x ) ⊆ X } (16)

x ∈ R ∗R X ⇒ [x]  ⊆ X and [x]   ⊆ X and

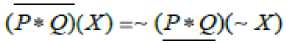
Finally we define topological types (or characterization) of Multi-granulation Rough Fuzzy Set as below

Definition 2.6: An incomplete information system is a pair denoted by S = (U, A) where U is a non-empty set of objects, P,Q ⊆ A be two attribute subsets, and X ∈ F(U) be a fuzzy set in U. Then

If ((P∗Q)(X))>0≠φand ((P∗Q)(X))>0≠ U,  then we say that X is roughly P∗ Q -definable (T1 or Type-1).(18)

If ((P∗Q) (X))>0= φ and ((P∗Q) (X))>0  ≠U, then we say that X is internally P∗ Q -undefinable (T2 or Type-2).(19)

If ( ( P ∗ Q ) (X)) >0 ≠ φ and (( P ∗ Q )(X)) >0 = U, then we say that X is externally P ∗ Q –undefinable (T3 or

Type-3).(20)

If ( ( P ∗ Q ) (X)) >0 = φ and (( P ∗ Q ) (X)) >0 = U, then we say that X is totally P ∗ Q –undefinable (T4 or Type-4). (21)

• III.    Results

• 3.1    Comparative Analysis

The results presented in this section are of two categories. In the first subsection we provide a comparative study of the two types of Multigranulations and the indiscernibility relation. In the second section we deal with the topological properties of fuzzy sets.

Let us denote the pessimistic Multigranular rough sets and the optimistic rough sets associated with R and S by R ∗ S and R+S respectively.

Theorem 3.1: For any X ⊆ U and two equivalence relations R and R defined over U, we have

R ∗ R X ⊆ R + R X ⊆ R n R X ⊆ R n R ₂ X

⊆ R + RX ⊆ R ∗ RX

Proof:   R ∗ R X ⊆ R + R X

• ^{1    2        1     2}                         (21)

It follows from the following:

⇒ [ x ]    ⊆ X or [ x ]    ⊆ X

R ₁ R ₂

⇒ x ∈ R + R X .

R + RX ⊆ R n R ₂ X .

It follows from the following:

x ∈ R + R X ⇒ [ x ]   ⊆ X or [ x ]    ⊆ X . But ,

[ x ] _R n _R  ⊆ [ x ] _R and [ x ] _{R  R} ⊆ [ x ] _R . So ,

[ x ] _{R 1 R 2}

⊆ X . Hence , x ∈ R R X .

Since RR is an equivalence relation, R n R X ⊆ R n R X follows from rough set property.                                           (23)

Now, we have

^1 П ^ № =~ VW~ ^X j^ + j^ (Л-) ^ j^ + 2^ (~ X) and

^ * Я₂ (X) =~ 2?! * Я₂ (~ X).

Also, for any two sets X and Y, So, the rest of the inclusions follow from (21), (22) and (23).

Note: All the inclusions in the above theorem can be strict. We provide the following example to establish this.

Example 3.1: Let us take

U = { e , e , e , e , e , e , e , e } and X = { e , e , e , e }.

Then

Let us take

U / R ₁ = {{ e ₁, e ₇},{ e ₂, e ₃, e ₄, e ₅, e ₆},{ e ₈}} and

U / R ₂ = {{ e ₁, e ₂},{ e ₃, e ₄, e ₅},{ e ₆, e ₇, e ₈}}.

Then

U / R n R ₂ = {{ e ₁},{ e ₂},{ e ₃, e ₄, e ₅},{ e ₆},{ e ₇},{ e ₈}}.

So,

R_x * R^X = ф ,R ₁ + R₂X = ^, e₂ , e ₈},

R 1 Q R 2 X = { e 1 , e ₂, e ₆, e 8 } = R 1 Q R ₂ X .

R ₁ + R₂X = { e ₁, e ₂, e ₆, e ₇, e ₈} and

R_x * R₂X = U .

So that

R_x * RX ^ R_x + RX * R П R₂X and

R_x П R₂X ^ R + R₂X ^ R * R₂X .

It is well known that

R R X maynotbeequaltoR R X .

Corollary 3.1.1: For any X c U ,

BN ( R П R )( X ) c BN ( R + R₂ )( X ) c BN ( R * R ₂ )( X ).

Corollary 3.1.2: For any X c U , X is rough w.r.t R 1 R 2 ^ X is rough w.r.t R_x + R ₂ ^ X is rough w.r.t R_x * R ₂.

Corollary 3.1.3: For any X c U , X is crisp w.r.t

We can extend the above results to the case when the number of granulations is more than two. For this we shall use the following notations:

Let P , P , P_m be m number of equivalence relations over U. Then we use the notations:

E m P- for optimisticmultigranulation

Пmi P. forpessimisticmultigranulationand m P for indiscernibility multigranulation

For any X c U and P₁, P₂,.. .P m being equivalence relations on U,we have

П ”1 Pi ^X c^^ X c n m_=x Pi X c ^^X ^X _£n m 1 PX .

Theorem 3.2: Let S = (U, A) be an incomplete information system where U denotes a universe of objects and A denotes an attribute set respectively. Let

R ₁, R₂ c A . Then for any X c U we have the following:

R * R2X c R + R2X c Rx UR2X c Rx UR2X c R + R2X c R * R2X.

Proof: (1) The proof of R_x * R₂X c R_x + R₂X is similar to that in Theorem 3.1.

Proof of R ₁ + R₂X c R_x U R₂X . This is part (1) of

Theorem 1 in [9].                                 (24)

Proof of R_x U R₂X c R_x U R₂X . Follows from the definitions of lower and upper multigranular approximations of sets in incomplete information systems.                                           (25)

Proof of R_x U R₂X c R i + R₂X . This is part (2) of

Theorem 1 in [9].                                 (26)

Proof of R1 + R2X c Ri * R2X. It is similar to that in Theorem 3.1.                                 (27)

Example 3.2 Let us take

U = { e 1 , e ₂, e ₃, e 4 , e 5 , e ₆, e ₇, e ₈} and X = { e 1 , e 2 , e ₆, e ₈}.

Then

Let us take L and P as two attributes in an incomplete IS having U as its domain such that

^U / SIM ⁽ L )   ^{{ {} e 1 , e 7 ^}, ^{{ e} 2 , e 3 , e 4 , e 5 , e 6 ^},^{{ e} 8 ^{} }} and

U / SIM ( P ) = {{ e 1 , e ₂ }, { e 1 , e ₂, e ₃, e 4 , e ₅, e ₆, e ₇, e ₈},

{ e ₂, e ₃, e ₄, e ₅},{ e ₂, e ₆, e ₇, e ₈}}.

So that

U / SIM ( LUP ) = {{ e 1 },{ e 2 , e₃, e 4 , e ₅ , e 6 }, { e 2 , e ₃ , e 4 , e ₅}, { e ₂, e ₆ } ,{ e ₇, e ₈}}.

Now,

L U P X = { e 1 , e 2 , e ₆, e ₈}, L\^PX = { e 1 , e 2 , e 3 , e 4 , e ₅, e 6 , e ₈}.

L + P X = { e 1 , e ₂}, L + PX = { e 1 , e 2 , e 3 , e 4 , e ₅, e 6 , e 7 , e ₈}.

L * P X = ф , L * PX = { e 1 , e 2 , e ₃, e 4 , e ₅, e ₆, e 7 , e ₈}.

Here,

L * P X ^ L + P X .        L + P X ^ L U P X      .

L U PX ^ L U PX .        L U PX ^ L + PX .

• So,    the inclusions in Theorem 2 can be strict .

Corollary 3.2.1: Let U be an incomplete IS. Then for any X c U ,

BN ( R_x U R ₂)( X ) c BN ( R + R ₂)( X )

c BN ( R_x * R ₂ )( X ).

Corollary 3.2.2: Let U be an incomplete IS. Then for any X c U, X is rough w.r.t R U R2 ^ X is rough w.r.t R + R2 ^ X is rough w.r.t R1 * R2.

Corollary 3.2.3: Let U be an incomplete IS. Then for any X c U , X is crisp w.r.t R ₁ * R ₂. ^ X is crisp w.r.t R + R ₂ ^ X is crisp w.r.t R ₁ U R ₂ .

Let S = ( U , A ) be an incomplete information system where U denotes a universe of objects and A denotes an attribute set respectively. Let R ₁, R ₂,... R^ c A . Then for any X c U we have the following:

Пm! RX c Zmi RX c um i RX c Um RiX iiii c z m1 RiX c n m1 RiX.

• 3.2    Topological Properties

• 3.2.1    Example for entry (1, 1)

New sets are formed from existing sets through set theoretic operations. This is true for both crisp sets and fuzzy sets. One would like to know the types of these new sets in order to apply them. This has been studied for crisp sets by Tripathy et al [11, 13] and also their generalisations. Similar problems have been tackled for Optimistic Multigranular crisp sets in [14], Optimistic Multigranular fuzzy sets in [15], Optimistic Multigranular intuitionistic fuzzy sets in [16, 17] and pessimistic Multigranular sets in [18]. In this section we shall determine types of the complement, union and intersection of pessimistic multi granular rough fuzzy sets (PMGRFS). These results will be useful for further studies in approximation of classifications and rule generation.

The table for the types of a fuzzy set X with respect to P * Q for its different possible types with respect to attribute subsets P and Q of A in an IS (U, R) remains same as that for a subset of X derived in [18]. As this is a several case, we provided examples for some entries in the table.

Let U - { a^ , a^ , a^ , a 4 , a 5 , a^ , a y, a ^ }.

U / SIM ( P ) - {{ a j, a ₇ },{ a ₂, a ₃}, { a ₄, a ₅ },{ a ₆, a _? },{ a ₈ }}

U / SIM ( Q ) - {{a1, a 7},{ a 2},{ a 3, a 4},{ a 5, a 6},{ a 7, a 8}}

LeiX = {(й!, 0.6), (Д₂, OX (д₃, OX (a₄,0.4), (a₅,0.5), (a₆.0.6), (a₇ ,0.7), (a_s, 0)} he a J^zp set and it ¹5 tower and upper approximations are as below.

№)_>0 = №_P 0 6), (^ A (a₃>ox (д₄, o.4x (a₅, 0.5), (^, 0.6), (fl₇,0.6), (a_s, 0)}^^ and

- X = {(a_v 0.4), (a₂ Л), ^ ,1), («₄,0.6), (p₅,0.5), («₆,0.4), (^.ОЗД,!»

CO" ^ = {(^OJ^JX (^,1), (fl4,0.5), (flj, 0.5), (a6,0.3), (^.OJX^.l)}

( P ( X )) > 0 - {( a 1,0.7),( a 2,0),( a 3,0),( a 4,0.5),( a ₅,0.5),( « 6,0.7), ( a 7,0.7), ( a 8,0)} * U .

Thus Xis of Type — 1 w.r .t . P .

( Q ( X ))>₀ - {( a 1, 0.6), ( a ₂,0), ( a ₃,0), ( a 4,0), ( a 5 ,0.5), ( a 6,0.5), ( a-, , 0), ( a^ , 0)} * ф and

( Q ( X ))>₀ - {( a 1 ,0.7), ( a 2 ,0), ( a 3 ,0.4), ( a ₄,0.4), ( a ₅,0.6), ( a 6 ,0.6), ( a 7 ,0.7),( a 8 ,0.7)} * U .

Thus X is of Type — 1 w.r.t . Q .

(( P * Q )( X ))>₀ - {( a _p0.6), ( a ₇, 0.6)} * ф and

(( P * Q )( X ))> 0 - {( a _p0.3),( a 7 ,0.3)} * U .

Thus X is of Type — 1 w . r . t . ( P * Q ).

• 3.2.2    Example for entry (1, 3)

Let U - { a _t, a ₂, a^ , a ₄, a ₅, a ₆, a ₇, a ₈ }.

U / SIM ( P ) - {{ a 1, a 7},{ a 2, a ₃},{ a ₄, a ₅},{ a 6, a 7},{ a 8}} U / SIM ( Q ) - {{ a 1, a ₇},{ a ₂},{ a 3, a ₄},{ a ₅, a ₆},{ a ₇, a ₈}}

Let X - {(a, 0.6), (a2,1), (a3,0), (a4,0.4), (a5,0.5), (a6,0.6),(a7,0.7),(a8,0)}.

( P ( X )) > 0 = {( « i, 0.6), ( a 2 ,0), ( a 3 ,0), ( a 4 ,0.4), ( a 5 ,0.4), ( a ₆,0.6),( a ₇,0.6),( a ₈,0)} * ф and

( P ( X )) > 0 - {( a „0.7),( a 2 ,1),( « з,1),( a 4 ,0.5),( a 5 ,0.5),

( a 6 ,0.7),( a 7 ,0.7),( a 8 ,0)} * U .

Thus X is of Type — 1 w . r . t . P .

( Q ( X )) > 0 - {( a , ,0.6),( a 2 ,1),( a 3 ,0.3),( a 4 ,0.5),( a 5 ,0.5),

( a ,0.7),( a ₇,0),( a ₈,0)} * ф and

( Q ( X )) 0 - {( a 1 ,0.7), ( a 2 ,1), ( a 3 ,0.4),( a 4 ,0.6), ( a 5 ,0.6),

( a 6 ,0.6),( a 7 ,0.7),( a 8 ,0.7)} - U .

Thus X is of Type — 3 w . r . t . Q .

(( P * Q )( X )) > 0 - {( a „0.6),( a ₇,0.7)} * ф and

(( P * Q )( X )) 0 - {( a _P0.7),( a 7 ,0.7)} * U .

Thus X is of Type — 1 w . r . t . ( P * Q )

Like the previous case, here also there is no change in the table. We provide an example for only one entry for illustrations.

• 3.2.3    Example to prove entry of row2

Let U = { a^ , a ₂, a^ , a^ , a^ , a^ , a^ , a^ }.

U / SIM ( P ) = {{ a 1, a ₇ },{ a 2, a 3 },{ a 4, a 5 },{ a 6 , a 7 },{ a 8}}

^U / SIM ⁽ Q ) = ^{{ a l , a 7 ^},{ a 2 ^{} {} a 3 , a 4 ^},{ a 5 , a 6 ^},{ a 7 , ^a 8 ^}}

Let X = {( a^ , 0.3), ( a ₂,0.5), ( a^ , 0.4), ( a ₄,0), ( a ₅,0.5),

( a , 0.6), ( a , 0), ( a , 0.8)} berough fuzzyset .

(( P * Q )( X )) >₀ =ф ==> (1) and

-X= {(a^ 1), (д₂, 0.7), (a₃, 0.5), (a₄,0.6),

(^,0 5), (^.0 4)^,!), (^,0 2)}

((P * 6)(- ^n - «“I - О- <>7 0 W =>(²)

(~ «P*Q)(? '^»>О = {(_Яр O) (a₂ O)} ^ф * U.

((Р^Х-ПХо * и

Thus X is of Type - 2 wz PFrom (2) above we have((P^QX-X^>0 * Ф

e(p*gx~^=((^*0(^))^ =^ (Л^О)) «р^Х-^Ко = ((^*SX~^»>o =^ = u.

Thus-X is of Type - 3 w.rZ P

• 3.3    Table for type of XY with respect to ( P * Q )

Like the earlier cases the table in [18], remains unchanged. However, as it is a general case, we provide a proof for two cases and illustrate that all entries are provide in other two cases.

Suppose X and Y are both of Type-1. Then

(( P * Q )( X )) >₀ * ф ,(( P * Q ) ( Y )) >₀ * ф ,

(( P * Q )( X )) >₀ * U and (( P * Q ) (Y )) >₀ * U .

From (2.13) it follows that

((P * Q)(X U Y )) >0 * ф.

But using (2.12) we see that

((P * Q)(X   Y)) has both the possibilities

of being equal or not equal to U.

So, X U Y can be of Type — 1 or of Type — 3.

• 3.3.1    Examples to prove entry (1,1)
  
  Case 1

Let U = { a^ , a^ , a^ , a^ , a^ , a^ , a^ , a^ }.

U / SIM ( P ) = {{ a i, a ₇},{ a 2, a 3, a 4, a 5, a 6, a 7},

{ a ₈}}

U / SIM ( Q ) = {{ a 1, a 7},{ a 1, a 2, a _§},{ a 3, a 4, a 5, a ₆, a 7}}

Let X = {( a^ , 0.6), ( a ₂,1), ( a^ , 0.3), ( a ₄,0), ( a ₅,0),

( a , 0), ( a , 0.3), ( a , 0.6)} and

Y = {( a1 ,0.5), ( a 2,1), ( a3 ,0.3), ( a 4,0), ( a 5,0),

( a , 0), ( a , 0.2), ( a , 0.6)} betworough fuzzy sets .

Then X U Y = {(ax, 0.6), (a2,1), (a3,0.3), (a4,0),

(a5, 0), (a6, 0), (a7, 0.3), (a8, 0.6)}

((P * Q)(X))>0 * {(a1,0.3), (a7,0.3)} * ф and

((P*Q)(X))>0 *{(a1,0.6),(a7,0.6)} *U.

Thus X is of Type — 1

((P*Q)(Y))>0 ={(a1,0.2),(a7,0.2)} *ф and

((P*Q)(Y))>0 = {(a1,0.5),(a7,0.5)} *U.

Thus Y is of Type — 1

((P * Q)(X U Y))>0 ={(a1,0.3), (a7,0.3)} *ф and

(( P * Q )( X U Y )) > 0 = {( a 1 ,0.6),( a 7 ,0.6)} * U .

Thus X U Y is of Type — 1

Let U = { a ₁, a ₂, a ₃, a ₄, a ₅, a ₆, a ₇, a ₈}.

U / SIM ( P ) = {{ a 1 , a 2 , a ₇},{ a 3 , a ₄, a ₅},{ a 6 , a 7 , a 8 }}

U / SIM ( Q ) = {{ a 1 , a 2 , a 6 , a ₇},{ a 3 , a 4 , a 5 },{ a 6 , a 7 , a 8 }}

X = {( a 1 ,0.2), ( a 2 ,0), ( a 3 ,0.4), ( a 4 ,0.5), ( a 5 ,0),

( a ,1), ( a ,1), ( a , 0.6)} and

Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.3), ( a 4 ,0), ( a 5 ,1),

( a , 0.1), ( a ₇, 0.2), ( a , 0.6)} be two rough fuzzy sets .

X U Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.4), ( a 4 ,0.5), ( a 5 ,1),( a 6 ,1),

( a ₇,1),( a ₈,0.6)}

(( P * Q )( X )) > o =ф and

((P*Q )( X )) > o = {( a 3,0.5),( a 4,0.5),( a 5,0.5)} * U .

Thus X is of Type — 1

(( P * Q )( Y)) > o = {( a 6,0.1), ( a 7,0.1), ( a 8,0.1)} * ф and

(( P * Q )( Y )) > 0 = {( a 6,0.6), ( a 7,0.6), ( a 8,0.6)} * U .

Thus Y is of Type — 1

(( P * Q )( X U Y )) > 0 = {( a ₃,0.4), ( a 4,0.4), ( a^ , 0.4), ( a^ , 0.6), ( a^ , 0.6), ( a ^, 0.6)} * ф and (( P * Q )( X U Y )) > 0 = U .

ThusX U Y is of Type — 3 w.r .t. (P * Q)

Let both X and Y be of Type 1 and Type 3.

Then from the properties of type 1 and type 3

( ( P * Q ) ( X )) >o * ф ,  ( ( P * Q ) (Y) ) >0 * ф ,

(( P * Q )(X)) >0 * U and ( ( P * Q )(Y)) >0 = U.

So, using (2.15) and (2.16) we get

(( P * Q ) ( X U Y ) ) >0 * ф and

(( P * Q ) ( XY ) ) >0 = U.

Hence XUY is of type 3 only.

The other cases can be similarly established.

• 3.3.2    Example to prove entry (2,1) in XUY table
  
  Case 1

Let U = { a ₁, a ₂, a^ , a ₄, a ₅, a ₆, a ₇, a^ }.

U I SIM ( P ) = {{ a^ , a ₇},{ a ₂, a ₃, a ₄, a ₅, a ₆, a ₇},{ a ₈}} U I SIM ( Q ) = {{ a 1, a ₇},{ a 1, a 2, a ₈},{ a ₃, a 4, a ₅, a 6, a ₇}}

Let X = {( a 1 ,0), ( a ₂ ,1), ( a 3 ,0.3), ( a ₄ ,0), ( a ₅ ,0), ( a ₆ ,0), ( a , 0.3), ( a , 0.6)} and

Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.3), ( a 4 ,0), ( a 5 ,0), ( a 6 ,0), ( a , 0.2), ( a , 0.6)} betworough fuzzy sets .

X U Y = {( a 1 ,0.5), ( a ₂,1), ( a ₃,0.3), ( a ₄,0), ( a 5 ,0), ( a ₆,0), ( a ₇, 0.3), ( a ₈, 0.6)}

((p*gx^))^ = Ф-

«P^QX" ^))_>0 = ««1, 0.7), U₇, 0.7)} * ф.

(~ (Ф*5)(~ JO^o = {(_ai. 0.3), (a₇,0.3)} * U.

((P4>X^))_>0 = {(^.О-ЗХ^О З)} * и.

X is of Type — 2 w.rl. (P * 0)

(( P * Q )( Y )) > 0 * ф .

(( P*Q )( Y )) > 0 * U .

Y is of Type — 1 w.r . t . ( P * Q )

(( P * Q )( X U Y )) > 0 = {( a 1 ,0.3), ( a 7 ,0.3)} * ф .

(( P * Q )( X U Y )) > 0 = {( a 1 ,0.5), ( a 7 ,0.5)} * U .

XUY is of Type — 1 w . r . t . ( P * Q )

Let U = { a ₃, a ₂ , a ₃ , a ₄, a 5 , a ₆, a 7 , a ₈ }

U I SIM ( P ) = {{a_x , a ₂, a ₇},{ a ₃, a ₄, a 5 }, { a ₆, a ₇, a ₈}}

U I SIM ( Q ) = {{ a 1 , a ₂, a ₆, a ₇},{ a ₃, a ₄, a ₅}, { a ₆, a ₇, a ₈}}

LetX = {( a_x ,0.2),( a ₂,0), ( a ₃,0.4),( a ₄,0.5),( a ₅,0),

( a ,0),( a ,1), ( a , 0.6)} and

Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.3), ( a 4 ,0), ( a 5 ,1),

( a , 0.1), ( a , 0.2), ( a , 0.6)} betworough fuzzy sets .

X U Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.4), ( a 4 ,0.5), ( a 5 ,1), ( a 6 , 0.1), ( a 7 ,1), ( a 8 , 0.6)}

(( P * Q )( X )) > 0 = {( a 6 ,0.6),( a 7 ,0.6),( a 8 ,0.6)} * ф .

(( P * Q )( X )) > 0 = {( a 3 ,0.5),( a 4 ,0.5),( a 5 ,0.5)} * U .

X is of Type — 1 w . r . t .  ( P * Q )

(( P * Q )( Y )) _{> 0} = {( a 6 ,0.1), ( a 7 ,0.1), ( a 8 ,0.1)} * ф .

(( P * Q )( Y )) > 0 = {( a ₆,0.4),( a 7 ,0.4),( a 8 ,0.4)} * U .

Y is of Type — 1 w . r . t .  ( P * Q )

((P^CX^U 7)^0 = {(аз,0.4),(_Я4,0.4),(й₃,0.4) (^ * ° ⁶) ("7 ’⁰ Or ("g. 0 6)} * ф.

^Р*еХ~<.х\ЗТ5)Хй^Ф

(- (Ф*0Х- (х U П)Х0 = (- I) = ^ ((^ё)(^иг)Х.0 = ^

JTU У is о/ Тур# — 3 w.r_f- (Р * О)

• 3.4    Table for type of XY with respect to ( P * Q )

We follow similar approach as in section 3.3 as in this case also table in [18] remains unchanged

Suppose X is of Type-1 and Y is of Type-3. Then

( ( P * Q ) ( X )) > о * ф ,( ( P * Q ) ( У )) > о * ф ,

(( P * Q )( X )) > 0 * U and (( P * Q )( У )) > 0 = U . From (2.14) it follows that

(( P * Q )( Х П У )) > 0 * и .

But using (2.11) we see that

((P*Q)(X Y)) has both the possibilities of being or not being equal to ф.

So ХПК can be of Type — 1 orType—2

• 3.4.1    Examples to prove entry (1,3)

Let U = { a , a ₂, a ₃, a ₄, a ₅, a ₆, a ₇, a ₈}.

U / SIM ( P ) = {{ a ,, a ₂, a_n },{ a ₃, a ₄, a ₅},

{ a ₆ , a ₇ , a ₈}}

U / SIM ( Q ) = {{a_x , a ₂, a ₆, a ₇ },{ a ₃, a ₄, a ₅},

{ a ₆ , a ₇ , a ₈}}

Let X = {( a_x , 0.5), ( a-, , 1), ( a₃ , 0.3), ( a^ , 0), ( a₅ ,1),

(a6, 0.1), (a7, 0.2), (a8, 0.6)} and У = {(ax, 0.5), (a2,1), (a3 0.3), (a4,0), (a5,1),

( a ,1), ( a , 0.2), ( a , 0.6)} betworough fuzzy sets .

X n У = {( a 1 , 0.5), ( a ₂,1), ( a 3 ,0.3), ( a 4 ,0), ( a ₅,1), ( a ₆, 0.1), ( a ₇, 0.2), ( a ₈, 0.6)}.

(( P * Q )( X )) > 0 = {( a 6 ,0.1),( a 7 ,0.1),( a 8 ,0.1)} * ф .

(( P * Q )( X^е )) > 0 = {( a 6 ,0.4),( a ₇,0.4),( a 8 ,0.4)}

(( P * Q )( X )) > 0 = {( a 6 ,0.6),( a 7 ,0.6),( a ₈,0.6)} * U .

X is of Type — 1 w.r.t . ( P * Q ).

(( P * Q )( У )) > 0 = {( a 6 ,0.2), ( a 7 ,0.2), ( a 8 ,0.2)} * ф .

(( P * Q )( У^е )) >0 = ф

(( P * Q )( У )) >0 = U .

X is of Type — 3 w.r.t. (P * Q).

(( P * Q )( X n У )) > ₀ = {( a 6 ,0.1), ( a 7 ,0.1), ( a_% ,0.1)} * ф .

(( P * Q )( X n У )) > 0 = {( a 6 ,0.6), ( a 7 ,0.6), ( a 8 ,0.6)} * U .

( X n У ) is of Type — 1 w.r . t . ( P * Q ).

Let X = {( a 1 ,0.5), ( a 2 ,1), ( a 3 0.3), ( a ₄,0), ( a 5 ,1), ( a 6 , 0.1), ( a 7 , 0.2), ( a 8 , 0.6)} and

У = {( a , , 0.5), ( a 2 ,1), ( a ₃ , 0.4), ( a 4 ,0.5), ( a 5 ,1), ( a , 0.1), ( a , 0), ( a ,1)} be two rough fuzzy sets .

X n У = {( a1 ,0.5), ( a ₂,1), ( a ₃,0.3), ( a 4 ,0), ( a 5 ,1), ( a ₆, 0.1), ( a ₇, 0), ( a ₈, 0.6)}.

((P^)^))>o = «^яб - °- !X ("7 - 0-1X («в - 0 1)> * Ф-((PfQX- X))_>0 = ^a₆ ,0.4), (a₇,0.4), (a_E, 0.4)} ( - (( P*G ) - J0)_>0 = ^a₆ ,0.6), (_Q1,0.6), (a_e ,0.6)} ((P^GXX))^ * U.

Xis of Type - 1 w.r.t. (P* Q\

((PfQXT))_>0 - {(a₃,0.4), («₄,0.4), (г7₅,0.4)}^^.

<(Р*е)(‘Г»>о = ^

(-((P*5) -У))>0 =-w

((РЧ?)(Г))>₀ - и.

X is of Type — 3 w.r .t. (P * P).

(( P * Q )( X n У ))>0 = ф .

(( P * Q )( X n У ))>0 = {( a 6,0.6),( a 7,0.6),( a ₈,0.6)} * U .

( X n У ) is of Type — 2 w . r . t . ( P * Q ).

Let X and Y be of Type 2 and Type 1 respectively. Then from the properties of type 2 and type 1 multi granular rough fuzzy sets we get (( P * Q ) (X)) >₀ = ф ,

( ( P * Q ) (Y)) >o = ф , ( ( P * Q ) (X)) >o * U and (( P * Q )(Y)) >0 * U.

So using properties (2.15) and (2.18) we get ( ( P * Q ) (X A Y)) >0 = ф and (( P * Q ) (X A Y)) >0 * U. So, XY is of type 2. This completes the proof. The other cases can be established similarly.

• 3.4.2    Example to prove entry (2,1)

Let U = { a^ , a ₂, a^ , a ₄, a ₅, a^ , a ₇, a ₈ }.

U / SIM ( P ) = {{ a 1 , a 2 , a 7 },{ a 3 , a 4 , a 5 }, { a 6 , a 7 , a 8 }}

U / SIM ( Q ) = {{ a ₁, a ₂, a ₆, a ₇ }, { a ₃, a ₄, a ₅ }, { a ₆, a ₇, a ₈}}

Let X = {( a , 0.5), ( a ₂,1), ( a ₃,0), ( a ₄,0.2), ( a ₅,0.3),

( a , 0), ( a ₇, 0.2), ( a , 0.4)} and

Y = {( a 1 ,0.5), ( a 2 ,1), ( a 3 ,0.4), ( a 4 ,0.2), ( a 5 ,0.3),

( a , 0.4), ( a , 0.2), ( a , 0.4)} be two rough fuzzy sets .

X n Y = {( a_v , 0.5), ( a ₂,1), ( a ₃,0), ( a ₄,0.2), ( a ₅,0.3), ( a ₆, 0), ( a ₇, 0.2), ( a ₈, 0.4)}.

(( P * Q )( X )) > 0 = ф and

(( P * Q )( X )) > 0 = {( a 3 ,0.3),( a ₄,0.3),( a 5 ,0.3),

( a ₆,0.4),( a ₇,0.4),( a ₈,0.4)} * U .

X is of Type - 2 w . r . t . ( P * Q ).

(( P * Q )( Y )) > 0 * ф and

(( P * Q )( Y )) > 0 = {( a 3 ,0.4),( a 4 ,0.4),( a 5 ,0.4),

( a ₆,0.4), ( a 7 ,0.4), ( a ₈,0.4)} * U .

Y is of Type - 1 w . r . t . ( P * Q ).

(( P * Q )( X n Y )) > 0 = ф and

(( P * Q )( X n Y )) > 0 = {( a 3 ,0.3), ( a 4 ,0.3), ( a 5 ,0.3),

( a ₆,0.4), ( a ₇,0.4), ( a ₈,0.4)} * U .

( X n Y ) is of Type - 2 w . r . t . ( P * Q ).

• IV. Conclusion

Topological properties of rough sets play a major role in real life applications. There are two extensions of this, single granulation based basic rough sets to multi granulation rough sets. These are termed as optimistic multi granular rough sets and pessimistic multi granular rough sets. Parallel properties for the optimistic case and its extension to handle fuzzy sets have been done in [14] and [15] respectively. Also our extension to handle intuitionistic fuzzy sets was done in [17]. In this paper we provided a comparative study of those multi granular rough sets with other such sets and established some interesting properties. Also, we extended the topological properties to the case of pessimistic multi granular rough fuzzy sets.

• [1]    Kryszkiewicz, K.: Rough set approach to incomplete information systems, Information Sciences, vol.112, (1998), pp.39 – 49.

• [2]    Liang, J.Y and Shi, Z.Z.: The information entropy, rough entropy and knowledge granulation in rough set theory, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol.12(1),(2001),pp. 37 – 46.

• [3]    Liang, J.Y, Shi, Z.Z., Li, D. Y. and Wierman, M. J.: The information entropy, rough entropy and knowledge granulation in incomplete information system, International Journal of general systems, vol.35(6), (2006),pp.641 – 654.

• [4]    Liang, J.Y and Li, D. Y.: Uncertainty and Knowledge acquisition in Information Systems, Science Press, Beijing, China, (2005).

• [5]    Pawlak, Z., Rough sets, Int. jour. of Computer and Information Sciences, 11 , (1982), pp.341-356.

• [6]    Pawlak, Z. : Rough sets: Theoretical aspects of reasoning about data, Kluwer academic publishers (London), (1991).

• [7]  Qian, Y.H and Liang, J.Y.: Rough set method

  based on Multi-granulations, Proceedings of the 5^th IEEE Conference on Cognitive Informatics, vol.1, (2006),pp.297 – 304.

• [8]    Qian, Y.H, Liang, J.Y. and Dang, C.Y.: MGRS in Incomplete Information Systems, IEEE Conference on Granular Computing,(2007),pp.163 -168.

• [9]  Qian, Y.H, Liang, J.Y. and Dang, C.Y.:

Incomplete Multigranulation Rough set, IEEE Transactions on Systems, Man and CyberneticsPart A: Systems and Humans, Vol.40, No.2, March 2010, pp.420 – 431.

• [10]    Qian, Y.H., Liang, J.Y and Dang, C.Y.: Pessimistic rough decision, in: Proceedings of RST 2010, Zhoushan, China, (2010), pp. 440-449.

• [11]    Tripathy, B.K.:    On Approximation of

  classifications, rough equalities and rough equivalences, Studies in Computational Intelligence, vol.174, Rough Set Theory: A True Landmark in Data Analysis, Springer Verlag, (2009), pp.85 - 136.

• [12]    Tripathy, B.K.:    Rough Sets on Fuzzy

  Approximation Spaces and Intuitionistic Fuzzy Approximation Spaces, Studies in Computational Intelligence, vol.174, Rough Set Theory: A True Landmark in Data Analysis, Springer Verlag, (2009), pp.03 - 44.

• [13]    Tripathy, B.K. and Mitra, A. : Topological Properties of Rough Sets and their Applications, International Journal of Granular Computing, Rough Sets and Intelligent Systems (IJGCRSIS), (Switzerland),vol.1, no.4, (2010) , pp.355-369.

• [14]    Tripathy, B.K. and Raghavan, R.: On Some Topological Properties of Multigranular Rough Sets, Journal of Advances in Applied science Research, Vol.2, no.3, (2011), pp.536-543.

• [15]    Tripathy, B. K. and Nagaraju, M. : Topological Properties of Incomplete Multigranulation Based on Rough Fuzzy Sets, Global Trends in Information Systems and Software Applications, Springer Verlag, ObCom2011, Part II S CCIS 270, (2012) , pp.92-102

• [16]    Tripathy, B.K., Panda, G.K. and Mitra, A.: Incomplete Multigranulation Based on Rough Intuitionistic Fuzzy Sets, In: Universal Journal of Applied Computer Science and Technology (UNIASCIT), Vol.2 (1), (Jan 2012), pp.118-124.

• [17]    Tripathy, B.K., Panda, G.K. and Mitra, A.: Some Concepts of Incomplete Multigranulation based on Rough Intuitionistic Fuzzy Sets, In: proceedings of the 2^nd International Conference on Computer Science, Engineering and Applications (ICCSEA, 2012), New Delhi, Advances in Intelligent and Soft Computing Book Series, Springer, (May 2012), pp.683-694.

• [18]    Tripathy, B.K. and Nagaraju, M.: On Some Topological     Properties     of     Pessimistic

  Multigranular Rough Sets, International Journal of Intelligent Systems and Applications, Vol.4, No.8, (2012) , pp.10-17.

• [19]    Wu, M. and Kou, G.: Fuzzy Rough Set Model Based on Multi-Granulations, In: proceedings of the 2010 2^nd International Conference on Computer Engineering and Technology, (2010), pp.V2-71-75.

  Authors’ Profiles

  
  
  

  Dr. B.K. Tripathy (1957- ), male, is a senior professor in the school of computing sciences and engineering, VIT University, at Vellore, India. He has published more than 160 technical papers in international journals/ proceedings of international conferences/ edited book chapters of reputed

publications like Springer, IGI and guided 12 students for PhD so far. He is a member/life member of international professional associations like IEEE, ACM, IRSS, CSI, IMS, OITS, OMS, IACSIT, IST, and ACEEE. Dr.Tripathy is a reviewer of around 20 international journals which include IEEE, World Scientific, Springer and Science Direct publications. Also, he is in the editorial board of at least 10 international journals. His current research interest includes Fuzzy sets and systems, Rough sets and knowledge engineering, Granular computing, soft computing, bag theory, data clustering, database anonymisation, list theory and social network analysis.

Prof. M. Nagaraju (1969- ), male, Assistant Professor (senior), school of computing science and engineering (SCSE), VIT University, at Vellore, India. He is pursuing his Ph.D. Degree in computer science and engineering(CSE) from the same school. He is a life member in professional associations like ISTE and CSI. He is also a member of International Rough Set Society (IRSS). His research directions including Rough Sets and Systems, Granular Computing, Intelligent Systems and Soft Computing.