A Conic Radon-based Convolutional Neural Network for Image Recognition

Object recognition is considered to be a highly important vision task in computer vision. It has considerably been applied in a multitude of applications such as object tracking, vehicle parking systems, biometric applications and surveillance purposes. The classification methods are constituted of two basic steps: features extraction and classification task. First, features are built on from images and are then given to multiple classifiers. Therefore, the classification performance mainly depends on the features and classifiers. The classical Radon transformation (RT) [1]

is a successful tool for feature extraction that integrates straight lines from a one 2D image. The use of RT has not been restricted to recognizing segments in the image. Several researchers have exploited RT to recognize more complex shapes. RT was then used as a basic tool for various shape descriptors. The shape descriptors defined from the RT generally exploit its mathematical properties such as invariance with respect to geometric distortions such as translation, rotation and change of scale. Multiple applications using RT were realized such as detection of centerline [2], biometric identification such as iris identification [3] and object recognition [4]. Since the RT has shown success in different image processing areas, several researches have been carried out to generalize the RT in order to directly detect complex shapes, namely: circles, arcs of circles, broken lines... etc. Therefore, the generalized Radon Transform (GRT) was introduced as the sum of a function on a family of geometric functions other than straight lines. Two families of the GRT formalisms have been emerged. The first includes approaches that focused on an analytical formalism. A discretization then allows mapping from continuous to discrete domains [5, 6, 7]. However, there are other types of discrete RT transformations that based on algorithms applied directly to the image [8, 9, 10, 11].

Deep neural networks have received special attention in the last years as regards to their efficiency in recognizing complex patterns [12]. In fact, deep neural networks have found applications in different fields such as image classification [13], recognition of digit [14] and face recognition [15]. In this work, we propose a new image classification approach entitled CRT-CNN which extracts global features by the use of the CRT which are further combined with the Convolutional Neural Networks (CNN) for the classification task. Good classification rate and less computational complexity are our main objectives in this work.

This paper is structured as follows: section 2 presents a review of the state of the art methods. Afterwards, section 3 presents a little description of the conic Radon transform as well as the convolutional neural Networks. We then present our deep architecture for image classification. We analyze the experimental results in section 4. In final, section 5 presents a conclusion of the paper.

2.    Related Works

In this section, we review the state of the art methods of image classification. There are two principal classes of image classification: Explicit features based approaches and Implicit features extraction methods by convolutional networks We focus on some works of the first category.

The methods of features extraction can be categorized into two classes: local and global features extraction. Local approaches are built on some key points. The most popular features are histogram of oriented gradients (HOG) [16], scale invariant feature transform [17, 18]. HOG is based on the histogram of intensity gradients of an object shape. SIFT consists of turning images into a collection of local feature vectors which are invariant to translation, scaling, and rotation.

Different from local features, global features do not consider certain interest points but they take into account the image as a whole. Usual methods apply the Radon transform to extract global features.

The RT is applied for definition of biometric descriptors [19]. The authors defined a RT feature vector from hand images in the authentication process. Besides, RT is applied for face recognition and provides robustness to many illumination and distortion changes. However, the RT obtained features are relative to a predefined number of projection angles and not to the entire image.

Hasegawa et al. proposed an approach for object recognition with the use of the histogram of RT [20]. It was shown that the method is invariant to rotation, translation and scaling. The authors computed an angle correlation matrix and used the dynamic time incrementation to the angle coordinate to attempt robustness to transformations. But it presents sensitivity to noise.

Another pattern recognition method based on classical RT is the GR-signature proposed by Hentati et al [21]. It is based on the combination of RT and the Gradient operator for generalized pattern recognition. The method consists in applying the gradient to the matrix resulting from the application of the RT. Thus, the authors have used the GR-signature to introduce a new rectangularity measurement metric. It has been proven the GR-signature to be robust against noise and deformation.

Besides, the RT was used to recognize features such as polygon curves. The authors proposed a measure for shape polygonality as a metric for object classification [22].

However, these approaches based on classical RT detect only lines. Recently, researches have focused on detecting more than linear shapes.

Elouedi et al. defined the Multidirectional Generalized Radon Transform (GMDRT) [8]. It is an extension of Beylkin’s Discrete Radon Transformation (DRT) [23].

In 1987, Beylkin introduced the DRT defined to recognize parameterized curves which are translated along the horizontal axis. The GMDRT then generalizes the DRT to allow the detection of curves and geometric objects of the image independently of their orientations.

The major drawbacks of this transform are slowness and huge memory cost due to the large number of curves or objects projections.

The polynomial discrete Radon transform (PDRT) maps polynomial curves into peaks in the parameter space [10]. This approach is dedicated to detect only polynomial curves. This approach is applied to fingerprint identification [24].

It presents a shape descriptor in order to identify a person through their fingerprints. This identification is robust to geometric transformations such as translation and rotation. In [25], the authors extend the GMDRT. The composed shape-invariant Radon transform detects objects of complex shapes. This approach decomposes complex objects into basic shapes and then the Radon transform is used on the elements of an object instead of the whole object. This method allows the reduction of the number of projections in Radon transform by the selection of the most important primitives for each object.

In this paper, we define a generalized Radon transform to detect and recognize sophisticated features. The CRT was presented in [26] and is defined to integrate image over conic sections.

In addition to Radon, the CNN has achieved great results in various object classification applications [27, 28].

The deep architecture AlexNet achieved the best accuracy rate on the ImageNet dataset in the ILSVRC-2012 competition [13]. The network is composed of five convolutional layers, max-pooling or ReLU layers, and three fully connected layers with a final 1000 outputs. Data augmentation techniques were added in this architecture to improve results on the used benchmark. Generally, deep learning applications require complex architectures and big size of training data to achieve the most optimal results.

Kheradpisheh et al. proposed a deep spiking neural networks composed of several convolutional layers which are trainable with the spike-timing dependent plasticity (STDP) [29]. The STDP increases the learning of features corresponding to prototypical patterns that were both salient and frequent.

Instead of applying CNN on original images, several methods have used descriptors as input to CNN architectures. The authors in [30] extract from facial expressions fixed numbers of SIFT features which were thereafter used as an input matrix to CNN architecture.

Hayat et al. defined a deep learning approach called the Template Deep Reconstruction Model (TDRM) [31]. They used an encoder to define models specific for classes for training sets. TDRM is based on hand crafted features and requires fine tuning of parameters to refine results. It also requires a heavy computational time for training.

Plant image classification progress has increased in these years due to deep learning techniques. Several researchers were interested in CNN for leaf classification. A review by Zhou et al. [32] presented a study of recent CNN models. The authors reviewed deep learning models for plant image classification such as ResNet, DenseNet and MobileNet [32]. Through their study, they proved that DenseNet achieved the best results in leaf datasets with accuracy of 100%. All remaining Deep Learning models achieved classification accuracy of around 75%.

A study by Barre et al. [33] was based on an overall CNN architecture called LeafNet. This model is based on the concept of modules. Each module is composed of 2 convolutional layers and a MAX-pooling layer. The whole CNN architecture of LeafNet is constituted of five modules followed by a last convolution layer with a MAX pooling layer and ended with three fully connected layers.

As similar to Leaf net [33], Dual-Path Convolutional Neural Network architecture was based on double deep architectures [34]. It contains two branches, one for learning shape features and the second for learning texture features.

Kaya et al. have employed transfer learning to detect plant for leaf classification [35]. After that, they used logistic regression for leaf classification. Their approach achieved an accuracy of 97% using VGG16 and SVM and 99% using VGG16 and LDA.

These different networks presented above need a lot of parameters in the training process. However, our approach aims to reduce parameter number.

Several CNN approaches have been employed in the traffic signs classification. They achieved excellent results on GTSRB dataset. However, the majority of them have focused on accuracy performance instead of the number of parameters, which leads applications of traffic signs classification to be unadapted for real time scenarios.

In [36], the authors proposed a MicronNet, a highly compact deep convolutional neural network for real-time traffic sign recognition. This network achieved good results in terms of accuracy and parameter requirements.

Recently, authors in [37] have used Hough transform which represents a variant of classical RT and CNN for classification. They have reached performance close to state of the art. However, the authors do not provide information about the number of required parameters. In our proposed CRT-CNN method, we try to join on high accuracy with few computational parameters.

Our contribution in this work is to study the sequential employment of conic Radon transform for feature extraction and the convolutional neural networks applied on Radon space.

3.    Proposed Approach 3.1.    Conic Radon Transforms

The classical Radon transform (RT) in Euclidean space represents an integration of a function f(x, y) over straight lines. It is defined as:

ЯУЧр^,ф) = £⁺” J -” ^f(x,y)5(p — xсоs(ф') — ysiтl(ф))dxdy                     (1)

where 5(.) is the Dirac delta function, ф £ [0, n[ is the orientation of the line and p £] — от,+от[ is the distance between the origin of the coordinate system and the line.

The output of the RT is a parametric space where lines are replaced by luminous points (peaks) whose coordinates p and ф represent the corresponding straight lines parameters (p, фУ

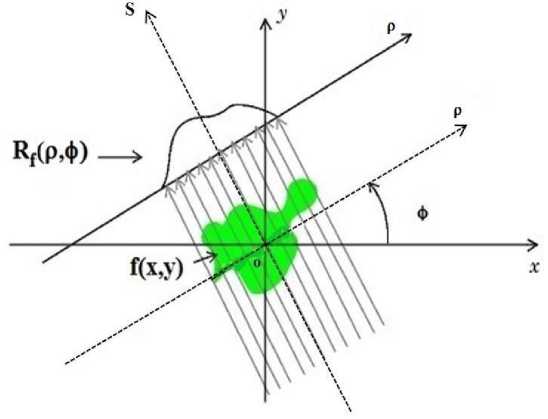
Fig.1. Classical Radon Transform.

As the classical RT is limited to line detection, The CRT was defined to detect conic sections of arbitrary positions and orientations [26].

A conic section can be an ellipse, a parabola, or a hyperbola, according to whether its eccentricity e value is less than, equal to, or greater than 1 (Fig. 2) .

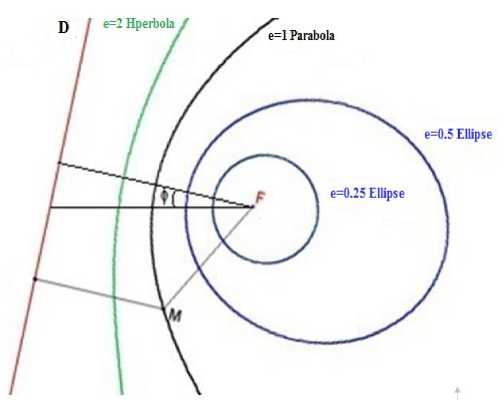
Fig.2. Different Types of Conic Sections: Ellipses (e = 0.25, e = 0.5), Parabola (e = 1) and Hyperbola (e = 2) with Fixed focus F and Directrix D.

The conic section of focus at the origin is represented by: for M(r, 0):

r =

p

1+e со5(6-ф)

where p is the conic parameter and ф corresponds to the orientation of the conic.

The generalized Radon transform represents an integration of a function f(x,y^ over conic sections in the plane. It is defined as:

Rсf(xF,yF,p,ф,e') = jcf(x,y)ds where ds denotes the integration measure on this conic section.

Rcf(xF,yF,p,(p,e) = Jy f (---^——cosCy + ф) + xF,---^——sinCy + ф) + yF)

1+e cos(y)                  F 1+e cos(y)                  F

P

V1+e 2 +2 e cos(y) (1+e cos(y))²

dy

where y = 9 — ф.

The CRT space is according to five parameters which are the coordinates of the focus x_F and y_F, the orientation angle ф, the conic parameter p, and the eccentricity e. (Fig .3) .

Fig.3. The Result of the CRT on (a) is the (x_F,y_F,p, ф, e) Parameters Space where (b) presents 2D View of CRT Space (e = 1, x_F = y_F = 0). Each of the Peaks Corresponds to the Parameters (ф, p) of the Curves.

The basic idea in this work is to apply the CRT in order to extract image’s global features and input the result into CNN in the purpose of achieving an accurate classification.

The features extraction task is reduced to the simple selection of peaks from Radon space. In fact, the integration of an image over curves maps image curves to high leveled points (peaks) in the obtained Radon space.

This paper defines a new object descriptor based on RT over lines, circles and parabolas.

In fact, the result of the CRT over parabolas with fixed focus is a (p, ф) Radon space. We putted the angle ф in [0,180 ° [ and p in [1, ^N_x + № 2 ]. N_x, N_y are the size of image.

We varied the position of focus to extract all potential parabolas. We varied the focus coordinates by considering the increment step 10.

Each peak in the Radon space reflects a parabola in the initial image. We have extracted these peaks in order to define our descriptor.

The same process is applied on the circular Radon transform and the linear Radon transform. We have extracted the luminous points which correspond to circles and lines.

The Radon based descriptor sets all extracted peaks into one final feature vector. This step aims to extract discriminant information that increases the object classification accuracy. The resulting feature vector is reshaped to form a matrix that can be associated with original image and used for the CNN input.

• 3.2.    Image Classification with Convolutional Neural Networks

The Convolutional Neural Networks (CNN) architecture is based on a succession of transformations associating linear and nonlinear operations. These transformations are used to recognize data at different abstraction levels. CNN are simply defined as deep architectures since they connect a hierarchy of layers. The outputs of a layer are the next layers inputs.

The architecture of a typical CNN consists of three main layers, namely: Convolutional Layer, Pooling Layer, and Fully-Connected Layer.

Our intent is to propose a new CNN architecture applied on a Radon descriptor which is derived from (circular, parabolic and linear) Radon space. Our goal is to reach competitive accuracy with previous approaches and reduce the computing time of training phase.

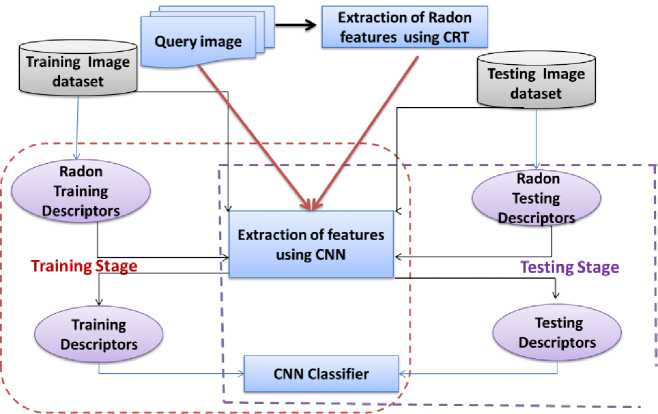
Fig.4. Proposed Approach.

In this work we try training models using small CNN architecture. The input of the network is nxn X k, where n depends on image size for each database and k = 4 is the channel number. Three channels are for image and the last channel is for the extracted Radon features.

Our CNN architecture is characterized by four convolutional layers, three max-pooling layers and fully-connected layer. Finally, the softmax output activation presents object classes. The output is one of the object classes.

The proposed architecture of the convolutional neural network is shown in Figure 5.

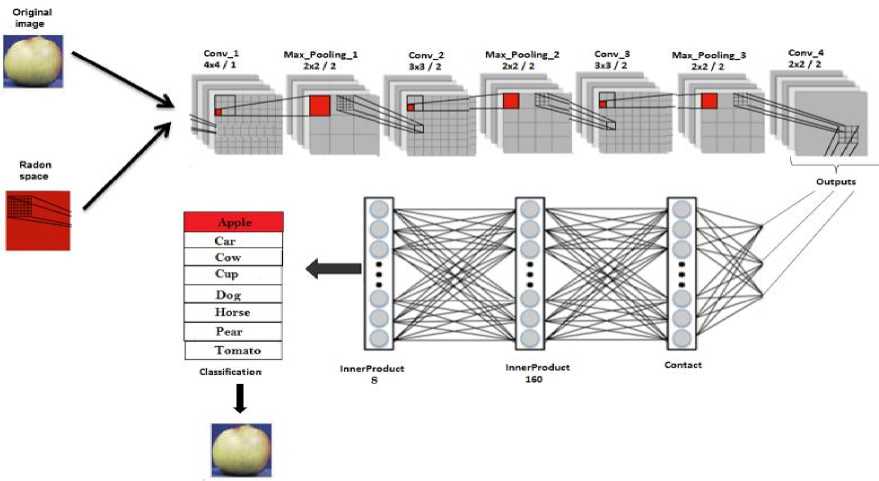
Fig.5. Architecture of the Convolutional Neural Network.

4.    Experiments

To validate the performance of our network, we carried out experiments on the most widely used benchmark for image classification.

In this section, we discuss the experimental results on three datasets. First, we describe databases and performance criteria. Then, we provide a comparative evaluation of our object classification approach compared to methods based on Radon transform. In addition, we also present comparative evaluations to methods based on CNN.

In order to make a qualitative analysis, we have opted for an experimental system similar to the previous works. The results of the different previous approaches for these datasets were gathered from their respective articles. Finally, we analyze the time complexity of our approach.

• 4.1.    Databases and Evaluation Metrics

In our work, we experiment on ETH80, FLAVIA and GTSRB databases.

• –    ETH80 dataset: It presents a good benchmark to show how the proposed method can handle multi-object categorization tasks. It is represented by eight categories: apples, pears, toy-cows, tomatoes, toy-horses, toy-dogs, toycars and cups. Each category is composed of 10 subcategories objects and 41 views per object are provided with different view angles (Fig.6 -a).

• –    FLAVIA dataset: It is a dataset for grouping plants by categories. It contains 1904 leaf images classified into 32 species as shown in Figure 6-b. This dataset suffers from the large intra-class and the small inter-class variations.

• –    GTSRB dataset: It is a popular dataset, composed of images corresponding to road signs. The image sizes vary from 15×15 to 250×250 pixels. Each image holds a road sign that belongs to one of the 43 classes of traffic sign (Fig .6- c) .

Similar to previous work, the images are cropped and resized to 48×48 pixels.

The 39209 images are selected for training and the rest 12630 images are used as the testing set.

Fig.6. a. ETH-80 Data set, b. FLAVIA Data set, c. GTSRB Data Set.

c

Several evaluation metrics can be used to confirm the following measures:

efficiency of classification methods. We retained the

– Accuracy rate, we have used the following expression:

Accuracy = ^tp^1°° %

where tp is the number of true classified objects and to is the total number of objects.

– Confusion matrix: it shows how the classification model is confused when it makes predictions.

Table 1. Architecture Configuration.

Layer type	Size/Stride	Output Dropout Probability
Data	n X n	-
Convolution 1	4 x 4 /1	20
Max_Pooling 1	2 x 2 / 2	-
Convolution 2	3 x 3 / 2	40
Max_Pooling 2	2 x 2 / 2	-
Convolution 3	3 x 3 / 2	60
Convolution 4	2 x 2 / 2	80
Max_Pooling 3	2 x 2 / 2	-
Fully Connected 1	-	160 Dropout=0.5
Fully Connected 2	-	8

Table 1 shows network configuration, the convolutional layers are applied with different kernel sizes (4x4, 3x3, 2x2) and different strides (1, 2). The Max_Pooling layers reduce the dimensionality of the responses of the convolutional layers with kernel size 2x2 and strice 2.

The parameters used for the training are listed in Table 2. For our model to provide best result, we have chosen the optimal value of these hyper-parameters empirically. We have examined the hyper-parameters in conjunction with the execution time of the training. We have fixed batch size to 20; this value is limited by your hardware’s memory. We have putted the parameters learning rate and Momentum of Stochastic Gradient Descent algorithm respectively to 0.001 and 0.9. These parameters involve in training convergence.

Table 2. Training Parameters.

Algorithm	Parameters
	Batch size = 20,
SGD	Epochs = 100, Learning rate = 0.001, Momentum = 0.9

• 4.2.    Image Classification Results

For the experiments, we have used Pytorch frame work on ubuntu 14.04 LTS and a GeForce GT 525M GPU, which has 2GB of memory.

Figure 7 shows the confusion matrix on ETH80 data set. We reached 96% as recognition rate. It can be shown that our proposed method achieves good performance on the eight categories. But we can observe a confusion between apple and Tomato class (around 5 % of apple objects are misclassified to Tomato objects).

In order to analyze the classification results, CRT-CNN is compared to other Radon transform approaches. These approaches are RT, PDRT, GMDRT and CCSIRT. These different Radon transforms are applied to ETH80 dataset and are used for feature extraction. SVM is used for classification task.

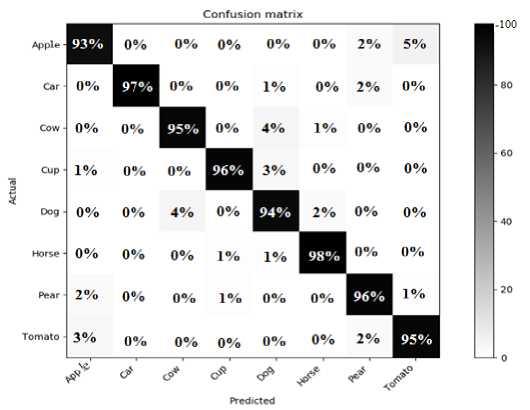
Fig.7. Confusion Matrix of Proposed Method on ETH80 Data Set.

Therefore, several experiments with respect to different sizes of labelled set and test set were performed. From Table 3, we can note that the accuracy of our CRT-CNN method performs the other Radon transform-based approaches for equal division (50% training, 50% test). We denote that the approaches based on the RT, GMDRT and PDRT give lower performances. Besides, CCSIRT provides good results. However, it depends on decomposition approach and the choice of the most pertinent primitives.

Table 3. Comparison Accuracy Scores with other RT Methods on ETH80 Dataset.

Approach	Accuracy
RT	69 %
GMDRT ([8])	75%
PDRT ([11])	78%
CCSIRT ([25])	94 %
Our proposed method	96 %

GMDRT: Multidirectional Generalized Radon Transform, PDRT: Polynomial Discrete Radon Transform, CCSIRT: Compound Complex Shape-Invariant Radon Transform.

Besides, we compared our technique with several image classification methods.

For each class object, five subcategories’ objects are selected for tests and the remaining instances are used for training.

Our work aims to achieve good accuracy and low parameters numbers. We have reached a good accuracy corresponding to small CNN. This small architecture does not require hard complexity for training phase, even in testing phase.

Table 4 presents that the overall classification accuracy of our approach on ETH80 data set outperforms the others previous methods except the TDRM.

This last achieves the best accuracy rate on ETH80 dataset. However, the training step in the TDRM requires a large dataset, it is computationally expensive.

Table 4. Comparison Accuracy Scores with others Deep Learning Methods on ETH80 Dataset.

Approach	Accuracy
CNN(AlexNet+SVM) ([29])	79.5 %
CNN(AlexNet) ([29])	94.2%
STDP ([29])	82.9%
TDRM ([31])	98.1%
Our proposed method	96 %

SDNN: Spike Deep Neural Network, TDRM: Template Deep Reconstruction Model Our CRT-CNN method shows good scores on FLAVIA dataset. This allows us to prove the effectiveness of our approachfor different datasets.

Table 5 shows the results based on our proposed method and other deep learning methods applied to FLAVIA dataset. The results confirm that our CRT-CNN approach presents a good accuracy rate for leaf classification. We achieved 98.7% of accuracy. However, all other deep leaning methods presented good results; these approaches need a lot of parameter numbers and so much time calculations.

Table 5. Overall Accuracy of Object Classification Methods on FLAVIA Dataset.

Approach	Accuracy
ResNet([32])	76%
MobileNet([32])	75.8%
DenseNet([32])	100%
Leaf net ([33])	97.9 %
Dual-path CNN([34])	99.7 %
VGG16+SVM([35])	97%
VGG16+LDA([35])	99%
Our proposed method	98.7%

Besides, we have got good results on traffic signs classification. Table 6 reveals that our CRT- CNN approach has performance of 99.1% on traffic signs dataset. This result is competitive to other deep learning methods. Radon transform plays a complementary role to the CNN. The association of CRT and CNN involve discriminative features for classification. The advantage of our approach is shown in terms of parameters numbers. Our model exceeds the whole previous works in terms of parameter requirement as shown in Table 6. Our proposed approach intents to get good accuracy and to reduce the number of required parameters, which makes traffic signs classification adopted for real-time applications.

Table 6. Comparison Accuracy Scores with others deep Learning Methods on GTSRB Dataset.

Approach	Accuracy	parameters number (M)
MicronNet ([36])	98.9%	0.51
Hough transform with CNN ([37])	98.2%	-
CNN (capsule networks) ([38])	97.6%	-
Multi-column CNN ([39])	99.4%	90
Hing Loss Trained CNN ([40])	99.6%	1.16
Our proposed method	99.1%	0.47

5. Conclusion

This article proposed a new approach for image classification that applies the conic Radon transform as a preprocessing for the Convolutional neural networks. Our model achieved a performance which is close to the previous works. Considerable refinement in terms of accuracy, and parameters requirement compared to related work are reflected in the proposed network. For object recognition, our model achieved an average accuracy equal to 96%. On the other hand, our model performed well in leaf images. It reached accuracy 98 % for FLAVIA dataset. In traffic signs classification, our proposed CRT-CNN method achieved an accuracy of 99%, with 0.47M parameters. As a perspective, our proposed method could be extended to other more complex and specific datasets.