A Cost-Aware Resource Selection for Dataintensive Applications in Cloud-oriented Data Centers

Published Online February 2011 in MECS

Following distributed computing, parallel computing, grid computing, utility computing, Web 2.0. etc., the computer industry and academia put forward cloud computing model [1], which achieves generalization and commercialization of these previous models in some

This work was supported by Open Foundation of State Key Laboratory for Novel Software Technology of Nanjing University (KFKT2009B22), Open Foundation of State Key Lab of Software Engineering of Wuhan University (SKLSE20080720) and selfdetermined and innovative research funds of WUT (2010-ZY-JS-030) respectively.

sense [2]. Cloud computing, the long-held dream of computing as a utility, has the potential to transform a large part of the IT industry, making software even more attractive as a service and shaping the way IT hardware is designed and purchase[3]. No doubts it would increasingly change the way people live and work. Cloud computing can be defined as “a type of parallel and distributed system consisting of a collection of interconnected and virtualized computers that are dynamically provisioned and presented as one or more unified computing resources based on service-level agreements established through negotiation between the service providers and consumers”[1].

As business application of data-intensive computing, cloud computing allows users to utilize on-demand computation, storage, data and services from around the world in a pay-as-you-go model [1]. At present, many of the major IT companies in the world, such as Google, Microsoft, IBM, Yahoo and Amazon etc., are active in promoting the research and application of cloud computing, and have begun to provide cloud commercial services [4].

Cloud applications need access large datasets that each may be replicated on different data centers [5,6,7] for improving data availability and reliability. As data plays a significant role in execution of data-intensive applications, the execution efficiency of application depends on the efficiency of transferring data to a large extent. On the other hand, due to cloud computing is a model of business computing, the economic cost of each replica itself can never be overlooked.

Furthermore, for one and the same data set, whose multiple replicas stored on different data centers [8] in cloud computing environment, the access costs are different on different data centers, just like the economic phenomenon in real world. Here it becomes very important to make an optimal resource selection. Therefore, how to select a set of resources (or data centers) for accessing replicas required and an appropriate one among them on which a virtual machine can be created for executing task such that the execution efficiency is high and the access cost is low as far as possible simultaneously is a challenging and urgent problem.

Based on the consideration detailed above, in this paper we plan to propose a cost-aware resource selection strategy for a data-intensive application to meet the two demands as far as possible. This paper makes two contributions: firstly, it models the problem of resource selection as an instance of Weighted Set Covering Problem (WSCP), and proposes a cost-aware resource selection strategy; second, it applies a WSCP heuristic for the problem to get an approximately optimal resource set for each task, and compares the heuristic against other algorithms through extensive simulations.

The rest of the paper is organized as follows: Section II introduces previous work in replica selection strategy in data-intensive environment. Section III introduces the evaluation model used in this research. Section IV details a cost-aware resource selection strategy, and proposes a WSCP-based heuristic to obtain an approximately solution. In section V, the proposed algorithm is evaluated in cloud simulator CloudSim and the results are presented. Finally, the paper was concluded in section VI.

• II.    R ELATED W ORK

The problem of resource selection in distributed environment has received lots of attention in recent years. In many previous works, resource selection refers to the selection of computational resource in grid environment. In [10], the authors presented a resource selection model using decision theory for selecting the best machine to run a task. In [11], they proposed an algorithm for resource selection problem of computational grids, based on the resource-availability prediction using frequent workload patterns.

Recently, with the rapid development of data-intensive computing, many researchers turned their attention to resource selection of data-intensive environment, such as data grid [12]. In data-intensive environment, besides computational resources, resources to be selected include data resources selection, which is equivalent to replica selection in data grid.

In [13], the author proposed Economy-Based File Replication Strategy for a Data Grid. It used an auction protocol to select the cheapest replica of a data set by a job running on computing element, which is lack consideration of the selection of computational resource.

In [8], Srikumar et al proposed a SCP-based TreeSearch heuristic (SCP) to minimize data transfer time, a large proportion in the total completion time of the job. However, the value of each remote data replica itself is not taken into account in their paper.

However, as cloud computing is a model of business computing, the value of data itself, represented by the economic cost of each replica, is an important aspect that cannot be neglected in practice. Therefore, based on [8], we propose a more general model. We made some improvements by considering the economic cost of each replica itself, besides data transfer time. In this paper, we try to achieve a best comprehensive effect for both demands, and apply our approach into cloud computing environment, a more promising field. What’s more, with the development of information technology, the data itself is becoming more and more valuable. Therefore, we believe in our work in this paper is more realistic and valuable in the near future.

• III.    M ODLE

A cloud environment can be considered as a set of M data centers D = { d 1 ,d 2 ,...,d_M }, which are connected by links of different bandwidths. For an application composed of a set of N independent tasks (or jobs) J = { Jv j 2 ,-, J n }( N >>  M ), each job j £ J , requires a set of K datasets, denoted by F ^j , that are distributed on a subset of D .

Consider a task j that has been submitted to a VM, which is created on data center d , for execution. For each dataset f £ F^j , the time needed to transfer it from d _f to d is denoted by Tt ( f , d_f , d ). The estimated data transfer time for the task, Tt ( j ), is the maximum value of all the times for transferring all the datasets required by the task. In this case, the estimated transfer time can be given by the equation as follows:

Tt ( j ) = MAX (Tt ( f , d f , d )) (1) f £ F

Here, the transfer time Tt ( f , d _f , d ) is denoted as following [8]:

Tt(f , d_f , r ) = R _ t ( d_f ) + Size(f )/ BW ( Link(d f , d )) (2) Where R _ t ( d _f ) is the time span from requesting for d _f to getting the first byte of f .And Size ( f ) BW ( Link ( d_f , d )) in equation (2) denotes the practical transfer time on the link.

In addition, the data access cost C ( j ) in our research is a function of c ( f ) , the access cost of each replica f . Here, we consider that each replica, whether on local data center or on remote data center, has its economic cost. The total cost of all the datasets required by j , C ( j ) , can be described as following:

C ( J ) = S ^c ( f ) (3) f £ F’

• IV.    C OST A WARE R ESOURCE S ELECTION

The paper concentrates on the selection of resources, that is, to select a data center for creating VM to submit the task and several other data centers for accessing replicas required by the task. The method for the problem adopted here is: firstly, to find a set of data centers for the task to access all the replicas required, and then to find an appropriate data center among them for creating a VM to execute the task. Here we select the one who has the minimum transfer time from other data centers in the set of all. Our aim is to reduce data transfer times and access cost of data by selecting an appropriate set of data centers. In this section, we propose a costaware resource selection for finding a set of data centers such that every data center selected contains replicas required as more as possible for reducing transfer times, while the total access cost of these replicas is as low as possible. That is to select data resources with lowest average access cost of replicas.

• A.    Modelling

A cloud application can be considered as a set of independent tasks (or jobs), each of which requires multiple datasets stored on different data centers at different costs. For a job j to be submitted to a VM that is created on data center d , the K datasets required, denoted by F ^j , are distributed on m different data centers at different costs, which can be shown in Fig. 1.

It can be translated into a form of adjacency matrix A = [ a ik ], 1 - i - P , 1 - k - K wherein a ik = Wi k ( w k > 0) if VM can access dataset f k from data center d_i at a cost of w_ik , which is abstracted as weight of f k ; and otherwise a ik = 0 , that is d i doesn’t contain f_k . The rows that contain a w_ik in a particular column are said to “cover” the column at cost of w_ik . The problem of finding an optimal data centers set such that each can “cover” replicas as more as possible, and the total access cost of replicas is as “cheap” as possible, can be considered as the problem of finding a set of data center, each of which has lowest average access cost of replicas. This problem is equivalent to the problem of finding an optimal set of rows to cover all the columns with the lowest average weight representing access cost. This problem has been studied extensively as the Weighted Set Covering Problem (WSCP)[14,15].

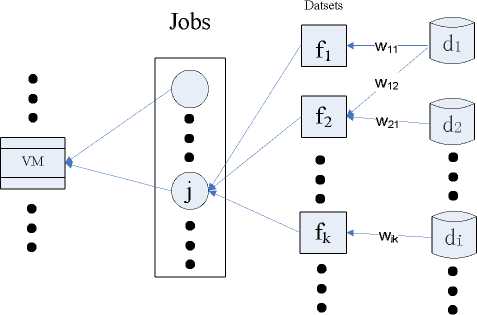
Fig.1 Cost-Aware Resource Selection

• B.    The WSCP-based Weighted-Greedy heuristic

The WSCP is an NP-complete problem [16], and the most common approximation algorithm applied to the WSCP is the Greedy strategy. Using the density (the ratio of cost to weight) thought for reference, we proposed a WSCP-based Weighted-Greedy heuristic (WSCP for short) to derive a nearly optimal set for covering all the datasets required by the task, as outlined below:

Step 1: Repeat until all the datasets have been covered.

Step 2: Pick the data center d_i such that it is the average “cheapest” to access replicas by selecting the minimal ratio according to formula W_d dd, n f| (where W_di is the cost of d_i by adding the w _ik in the row, and F is the set of replicas required by j and contained in d_i simultaneously), and then add it to the current candidate set.

After the two steps above, now we can get a set of mapping from each replica to data center that stores it. That is, we get a set of data centers to cover all the replicas required by the task.

The following step is to select an appropriate data center among these data centers selected previously, such that the transfer time to access replicas from other data centers in the set selected previously is minimum. Then create a VM on this data center selected finally for the task and submit the task to the VM. Here the selection of the final data center is mainly base on the proximity of the data centers. For each data center in the set of data centers selected previously, calculate the transfer time from other data centers to it for access replicas, and select the data center that has the minimum transfer time of all.

The algorithm is described in the following paragraphs. It outlines the WSCP heuristic that consists of three distinct phases: initialization, execution and termination. The following paragraphs will describe in detail.

Initialization (lines 1-2): The initialization starts with the creation of the adjacency matrix A for a task, with data centers forming the rows and datasets forming the columns. In the execution, the set B keeps the current mapping from every dataset to data center selected to access it, E contains the datasets already covered so far, L keeps the data centers that be selected for covering all the datasets required by the task and the variable z keeps track of the value of the completion time offered by the current solution set. And the procedure begins with B = Ф , E = Ф , L = Ф and z = ж .

Execution (lines 5-18): During execution, if the set of replicas covered E doesn’t include all the replicas required by the task, sort the rows of the matrix A in the ascending order by the ratio of the sum of nonzero numbers in a row to the number of them according to the formula Wdl\d n F| .Thus, every time the cheapest replicas can be selected. Then, the matrix is searched sequentially starting from the 0th row (or data center) in A . Then find a set of replicas covered by data center d0 , represented by F0j , which is a subset ofF j , the set of data centers required by task j . After that, put the mapping from f ∈ F0j to d0 into setB , add d0 to L , and add F0j toE . Then go on try the next data center to cover F j , until E = F j , that is all the datasets required by task j has been covered. At this point, B represents the one and only solution set of data centers produced by the heuristic that covers all the datasets. Then for each data center di ∈ D , the function MTransT(B) computes the expected value z of total transfer time fromdi to

Algorithm1. WSCP-based Weighted-Greedy heuristic

Begin Main

• 1    For a task j , create the adjacency matrix A with data centers forming the rows and datasets forming the columns

• 2    Initial solution set B = Φ , E = Φ , L = Φ and z = ∞ ; a data center d = NULL

• 3    Select(T, B, E, z)

• 4    S ^j ← {{ d }, L } where such that S ^j produces MTransT (B)

End Main

Select (T, B, E, z)

• 5    set a integer variable m = 0 as the index of row

• 6    while E dose not include all the files in F ^j

• 7    do

• 8    SortMaxtrix(A)

• 9    Get the d ₀ ， who has the cheapest data set according to the formula W_d /I d ∩ F I

• 10    Find the subset F ₀ ^j of F ^j covered in d_m

• 11    B ← B ∪ [ f ∈ F 0 ^j , d 0 ]

• 12    L ← L ∪ d ₀, E ← E ∪ F ₀ ^j

• 13    end while

• 14    z← MTransT (B)

• 15    End

MTransT(B)

• 16    Find d ∈ D such that the transfer time is minimum for the resource set S ^j ← {{ d }, L } and return the value

SortMaxtrix(A)

• 17    Sort the rows of A in the ascending order by the ratio of the sum of nonzero numbers in a row to the number of them according to the formula W_d /I d ∩ F I . Thus, the ratio of the 0 th row is lowest every time.

other data centers inL . Then compare the current value of z with the previous value produced in last iteration, and choose a smaller one. Then update the data center d selected to create VM to execute the task and the corresponding value of minimum transfer time z produced byd .

Termination (lines 4): The greedy heuristic can only get one solution L , so L as the final solution set, is combined with the data center that provide the minimum transfer time for the task. So the final resource set for task j , S ^j is a set of a data center set L and a data center in L for creating the VM to execute the task j .

• C.    Other approaches extended for resource selection

SCP—This mapping strategy, detailed in [8], is to find a resource set with the least number of data hosts for accessing the datasets required by a task, following by choosing a suitable computational resource to execute it. However, the selection of computational resource is not only based on the proximity of the data but also on its availability and performance as well. Thus, a minimum completion time is expected from the set of data hosts and computational resource. Its goal is to reduce the data transfer times by maximizing local access of datasets to minimize the completion time of the task. However, it pursued the execution efficiency regardless of the access cost of each remote replica itself when optimizing the process of resource selection.

Greedy—This strategy, presented in [17], builds the resource set by iterating through the list of replicas and making a Greedy choice for the data resources for accessing each replica at its lowest cost of all, followed by choosing an appropriate computational resource. Here, the approach to select the computational resource is to select the one that produced the minimum completion time. The completion time include the execution time, which is dependent on the power of computational resource, and data transfer time, which is concerned with the proximity of the data. Contrary to the SCP, this heuristic focused on the access cost of each remote dataset, partially ignoring the data transfer overhead, which is a large part of the total overhead.

Here it should be explained that, previously, these algorithms are used to select resources in data-intensive grid environment. And in this paper, we apply the strategy into Cloud environment and do some experiments in comparison with the algorithm proposed in this section.

• V.    P ERFORMANCE E VALUATION

Since it is not feasible to test different usages on real testbeds, it is easier to use simulations as a means of studying complex scenarios. In our simulation, we extend the CloudSim toolkit for simulating the function of data transferring between data centers.

To evaluate the performance of the WSCP-based model and related algorithm proposed in this paper, we experimentally compared this algorithm with other two ones (SCP and Greedy) through simulation respectively.

• A.    The extended CloudSim

CloudSim[19,20,21], leaded by Buyya, allows cloud customers to test their services in repeatable and controllable environment free of cost, and to turn the performance bottlenecks before deploying on real clouds[16]. It can provide a generalized and extensible simulation framework that enables seamless modeling, simulation and experimentation of emerging cloud computing infrastructures and application services. It is designed for studying various resource management approaches and scheduling algorithms in cloud environment. In CloudSim, users is modeled by a DatacenterBroker, which is responsible for mediating between users and service providers depending on users’ QoS (Quality of Service) requirements and deploys service tasks across Clouds[22].

In our experiments, we extended CloudSim for simulating the function of resource selection and data transferring between data centers. The DatacenterBroker class is extended by class SCPScheduler, WSCPScheduler, GreedyScheduler for the selection of the final datacenter, according to the three strategies respectively, which are described in previous section. And we compared the WSCP strategy with SCP, Greedy respectively in the experiments in several aspects, which will be detailed in next part.

• B.    Measures for Evaluation

In this part, we introduce three measures for evaluation for the algorithms respectively.

• (a)    Completion Time

Time here is the completion time of each job, and it includes not only the execution time, but also data transfer time. A smaller the total time to complete all the jobs is preferred.

• (b)    Access Cost

The access costs of one and the same replica are different on different data centers, and are produced by a random generator. A lower access cost is better as our aim is to select “cheapest” datasets.

• (c)    Mean percentage of data time

Here data time is the time for data transferring during the execution of each job. And the percentage of data time is calculated as a percentage of the total completion time for that job. The average of this measure over all the jobs then represents the mean impact of the data transfer time on the set of jobs or the application as a whole. A lower number is better as one of the algorithms presented so far has been to reduce the data transfer time[8].

• C.    Environment Configuration

The testbed modeled in this evaluation contains 6 data centers spread across six countries via high capacity network link. In our experiments, assuming the application can be converted into a set of independent jobs that each requires 5 dataset in this simulation and all replicas have been distributed on data centers before executing according to Uniform or Zipf distribution. In Uniform distribution, each dataset is equally likely to be replicated at any site, while a few datasets are distributed widely whereas most of datasets are found in one or two places in Zipf distribution [12]. The degree of replication is the maximum possible number of replicas of each dataset, which are distributed in the cloud environment at the beginning of the simulation. In this evaluation, it is 3. And the access cost of each replica is produced by a random generator; the value is between 1 and 9. We are concentrating on the variation of completion time, access cost and mean percentage of data time with the number of jobs from 50 to 300 at a step of 50.

The configuration for the experiment is as shown in

TABLE I.

S IMUALTION C ONFIGURATION

Heuristics	SCP WSCP Greedy
Distributions	Uniform /Zipf
FilesPerJob	5
dgreeOfReplication	3
No. of Jobs	50, 100, 150, 200, 250, 300

Table I.

• D.    Simulation Results

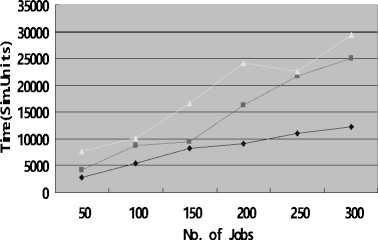
To evaluate the algorithm, we get the results by computing the average value of 5 experiments. Fig.2(a), Fig.2 (b) and Fig.2(c) show the comparison among the three algorithms under Uniform distribution in completion time, access cost and mean percentage of data time respectively, with the number of job increasing. And Fig.4 shows that in case of Zipf distribution.

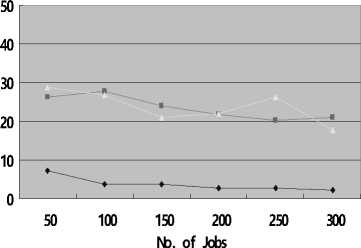
From Fig.2 and Fig.3, we can see that, whether in case of Uniform distribution or Zipf distribution, the execution efficiency is highest among the three algorithms, while Greedy can obtain the lowest access cost than others. This is due to SCP minimizes data transfer by maximizing local access; this can be demonstrated by Fig.2(c) and Fig.3(c), from which we can see the mean percentage of data time of SCP is the lowest. However, Greedy always chooses the “cheapest” one from multiple replicas of the same data set.

We can see another result that, in case of Zipf, the completion time is more than that in case of Uniform, which means that a job need access more replicas from remote data centers due to the rarer availability of datasets in Zipf distribution than in the Uniform distribution [8].

From Fig.2(a) and Fig.3(a), we can find that WSCP proposed in this paper is close to SCP in execution efficiency, and performs better than Greedy in most cases. Fig.2(b) and Fig.3(b) shows that WSCP is approximate to Greedy in selecting low cost replicas. That is to say, it can create a compromise between execution efficiency and economic performance, which can meet the both demands. Because it is established based on the ratio of cost to number of datasets covered, and selects the best resources according the ratio in the ascending order, so the data resource with lowest average cost is selected every time. This can guarantee the cost is low and the number of replicas covered every time is

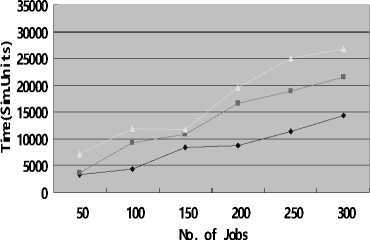
Fig.2(a) completion time in Uniform

—♦— SCP

—■— WSCP

Greedy

Fig.3(a) completion time in Zipf

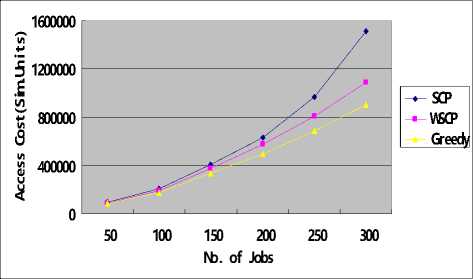
Fig.2(b) access cost in Uniform

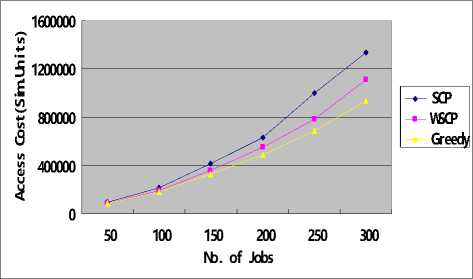
Fig.3(b) access cost in Zipf

—♦— SCP

—■— WSCP

Greedy

Fig.2(c) Mean Percentage of Data Time in Uniform high as far as possible simultaneously. Furthermore, the mean percentage of data time is lower than that of Greedy in most cases, from Fig.2(c) and Fig.4(c).

However, there is an interesting result here that is out of expectations: the mean percentage of data time by Greedy is lower than WSCP when the number of jobs is 300 in both distributions, and the effect in Zipf is more preferable than that in Uniform. That may can be attributed to the greedy strategy used in Greedy and WSCP seek the local optimal solution, which is not so steady in some cases. And another possible reason is the fact that Min-Min itself is not guaranteed to give the best schedules in every situation [23].

• VI.    C ONCLUSIONS

This paper presents the problem of selecting data centers for a cloud-based application composed of independent jobs that each requires multiple datasets,

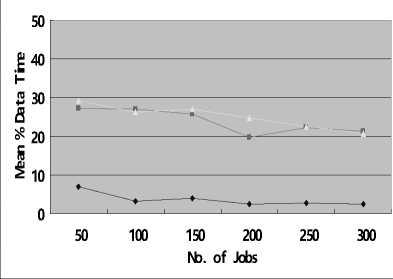
—♦— SCP

—■— WSCP

Greedy

Fig.3(c) Mean Percentage of Data Time in Zipf multiple replicas of each which are stored on different sites and accessed at different costs. It models the problem as an instance of WSCP, and proposes a WSCP-based Weighted-Greedy heuristic to produce an approximately optimal solution. Experiments showed that the performance in execution efficiency of WSCP-based heuristic is close to SCP-based heuristic, whose execution efficiency is highest of all, and its access cost is nearly the same as the Greedy, which provides the minimal access cost of all. Therefore, WSCP-based heuristic proposed in this paper can produce an approximately optimal solution in most cases to meet both execution efficiency and economic demands simultaneously.

A CKNOWLEDGMENT

This work was supported by Open Foundation of State Key Laboratory for Novel Software Technology of Nanjing University (KFKT2009B22), Open Foundation of State Key Lab of Software Engineering of Wuhan University (SKLSE20080720) and self-determined and innovative research funds of WUT (2010-ZY-JS-030) respectively. We would like to thank all the workmates in our Lab such a big warm family, for their kind support and advices.