A failure detector for crash recovery systems in cloud

Published Online July 2019 in MECS

Cloud computing has gained massive popularity in recent past owing to its abstraction of resources and on demand services. However, the high availability is essential to support reliable computing. Although, the performance parameters may indicate reliability of hardware components, wide variation in scalability may lead to inaccurate failure estimation. Moreover, the fault tolerance is essential because the computational nodes are highly dynamic. The effectiveness of a fault tolerance mechanism is determined by its accuracy and efficiency in failure detection. Though, cloud is an extension of conventional distributed systems, it has many added features, like high scalability, elasticity, and market driven dynamic pricing, which make it class apart. Hence, the failure detectors (FDs) as in [1] designed for conventional distributed systems are insufficient, inefficient or ineffective in cloud. Therefore, the design of correct Failure Detectors (FDs) for cloud is challenging. The paper presents a prospective implementation of reliable FD in crash-recovery model.

The distributed systems have widely been categorized as synchronous and asynchronous . In general, the synchronous systems use timeout mechanisms to detect failures. However, in a purely asynchronous environment, such timeout mechanism cannot be implemented as there is no bound on any kind of latency. Hence, it is ‘impossible’ to design and implement failure detector for purely asynchronous environment [2]. The impossibility, here, stems from the fact that it is not possible to distinguish between a crashed node and a very slow node without some time bound on response. Nevertheless, for all practical purposes it is reasonable to consider asynchronous model of computation that allows certain degree of synchrony. The clouds mostly exhibit dynamic asynchronous properties; however, a partial synchronous system can be simulated based on upper bounds of timeconstraint as per QoS requirements.

The FD modules are implemented at each computing node. It detects a crashed node on the basis of time out. Once a node is detected to be crashed it is prohibited permanently from participating in the computation. However, the prohibition is too strong and thus not preferable because a crashed node may recover soon. Thus, another class of FDs, termed unreliable FDs, makes better choice. The unreliable FDs, even after detecting a node suspected, may allow it to participate again provided the node recovers soon. In order to implement this idea, each node maintains a list of correct as well as suspected processes. A node may even fall in suspected list if it has become very slow. Thus, in case of unreliable

FD, the list of suspected processes maintained at various nodes may not be identical. Conventionally, FDs increment timeout period [3] whenever a process switches from suspect to correct state. However, such a mechanism may instigate an unending movement of nodes from suspect state to correct and vice versa. Generally, such anomalies may be avoided if every FD satisfies the following two properties to a certain degree [1]:

• (i)    Completeness : FD suspects all crashed processes.

• (ii)    Accuracy : There is a limit on wrong suspicion by an FD.

Further, above two properties have been reclassified as follows:

^  Strong Completeness: All  correct  processes suspect all crashed processes.

• >   Weak Completeness : Some correct processes

suspect all crashed processes.

• >    Strong Accuracy : A process is suspected only on crashing.

• >    Weak Accuracy : Not all correct processes are suspected.

• >    Eventual Strong Accuracy : After certain time, all correct processes are not suspected by other correct processes

• >    Eventual Weak Accuracy : After certain time, some correct processes are not suspected by other correct processes.

The above FD mechanism is limited to crash failure only. The system failure estimation is more challenging in crash recovery systems. They need checkpointing at regular intervals to enable rollback recovery. The crash recovery FD performs detection in two steps; firstly, the failed processes are declared crashed as and when they fail. Secondly, after recovery interval, the crashed processes are checked for possible revival. In literature, various methods are prevalent to checkpoint as well as recovery interval estimation. The proposed algorithm can successfully detect if a node fails to respond within timeout interval. In the first step, the crashed node is designated as suspected rather than crashed. Further, if a node fails to respond after the expiry of recovery interval, it is marked as crashed. The checkpoints are maintained to enable the system recovery.

The proposed algorithm considers BCMP [4] mixed multiclass networks for workflow modeling in cloud. The Machine Repairman model [5] is used to estimate checkpointing interval and time to recover. We present an analytical model in order to validate the theoretical accuracy of results. Also, the outcome of simulation experiments is in line with the results of static estimation for cloud environment.

Section 2 presents the relevant literature. Section 3 illustrates the proposed system model. Section 4 explains the analytical model followed by the description of proposed algorithm in section 5. Section 6 presents the proposed algorithm. Section 7 presents experimental validation. In the end, section 8 concludes the work.

• II.    Related Work

The FD in its prevalent form was first proposed by Chandra and Toueg [1]. The authors classified FD into eight categories based upon the type of correctness and accuracy. However, the Chandra-Toueg FD is inherently unreliable as delayed transmission may lead to incorrect detection. Further, based on crash failure assumption, correctness and accuracy have been adapted for recovery systems accordingly. Later, based on the concept of reducibility, Chandra et al. [6] proposed weakest failure detector. Fischer et al. [2] have shown that it is impossible to handle even a single failure in purely asynchronous systems. Nevertheless, the partial synchrony injections make failure detection possible. Dwork et al. [7] have considered two models of synchrony based on (upper and lower) bounds on message transmission delays, speed of processors, and stabilization interval. The message transmission latency and node failures have been observed to follow probabilistic distribution [8]. The registered set of nodes ping each other and if a node does not respond within certain timeout, sender node pings another set of k nodes. These k nodes, in turn, ping the previously non-responsive node(s). In case of timely response, the initiator node is informed about its presence in the system.

Any service is qualified by Quality of Service (QoS) measures. In literature, several QoS metrics have been proposed to estimate the efficiency of FD [9]. The primary metrics considered are based upon detection latency, time required to correct a faulty detection and frequency of mistaken detection. The proposed metrics are similar to dependency measures. Also, the metrics have been designed considering stochastic behavior using synchronized clocks with no drift. The algorithm considers variable timeout rather than fixed one.

The failure detectors have also been proposed for crash recovery systems by Aguilera et al. [10]. The frequency of failure and revival is maintained to establish the trustworthiness of a node. The suspicion level of a node is enhanced if the failure count continues to increase and it is used to declare failure eventually. However, if the failure count stabilizes, the process is considered trusted one. Secondly, the detection can be performed even without stable storage. The FD for crash recovery system has also been designed using dependability measures for QoS estimation and the node revival has been considered a regenerative process [11].

The early FDs were focused on failure detection mostly for static topology. However, the self-tuning FD (SFD adjusts time out value in view of QoS metrics and other system properties [12]. The implementation proceeds in terms of sliding window where arrival times are used to compute next fresh point interval for each message in sliding window. Turchetti et al. [13] proposed FD for Internet applications. The protocol is capable of managing multiple applications with varying QoS metrics simultaneously. It adjusts the timeout interval either by tuning it to maximum requirement or by equating it with GCD of all timeouts for all the components. The assumed bounds are best suited to the remote applications while GCD values are more apt for local applications.

Pannu et al. [14] proposed an adaptive FD for cloud using decision trees. It operates in two phases: adaptive prediction and decision-making. Wang  et al.  [15]

proposed FDKeeper, which has a layer based clustered architecture and takes into account three key parameters namely speed, scalability and heterogeneity. Liu et al. [16] proposed an accrual FD for cloud. Authors use heart beat inter arrival time to compute next timeout interval. However, unlike previous FDs, they advocate Weibull distribution instead of normal or exponential one.

In the literature, many failure detectors have been proposed to detect crash failure. However, crash recovery FD schemes require checkpointing and replication along with efficient detection. Checkpointing has been proposed to be modeled as a service in cloud [17]. VM replication schemes have been used by Mondal et al. [18] for recovery in cloud. Further, reactive recovery algorithms for SDN considering multiple faults have also been proposed [19]. Euclidean based approximation methods have also been used [20]. Markov process based model for failure estimation have also been considered in recovery systems [21]. However most of the previous techniques consider migration based approach for recovery .

The failure in clouds could be at any of the three levels: virtual machine (VM), processing machine (PM) and host. Failures at VMs and PMs have been modeled using Continuous Time Markov Chain (CTMC) [22] but the CTMC model suffers from state explosion problem. Nevertheless, our algorithm does not suffer from this problem because we have considered mixed multiclass models for performance modeling.

• III.    The System Model

The system consists of two-level hierarchy with broker at the top entrusted with resource management. The computational and system tasks are delegated to datacenters. The server (a.k.a. host) serves as terminal node in the system that performs the computation. The FD module at broker node detects failures in host machines. There are two types of processes, called computational processes and system processes . The computational processes, introduced by broker node, have been modeled as open class of jobs whose arrival and service times follow exponential distribution. The system processes comprise of heartbeat messages that propagate from broker node to the datacenter and further to respective hosts. At any given time, for each host, one heartbeat is under circulation. The successive heartbeat message is initiated only upon successful circulation of the earlier one. Though single heartbeat transmission incurs detection latency, the minimum timeout value compensates for the same. Fig.1 depicts the state diagram of host nodes. Fig.2 illustrates the system architecture.

Further, a host can be in any of the three states: working, failed and recovering.

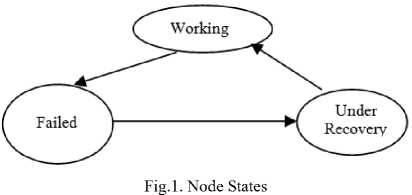
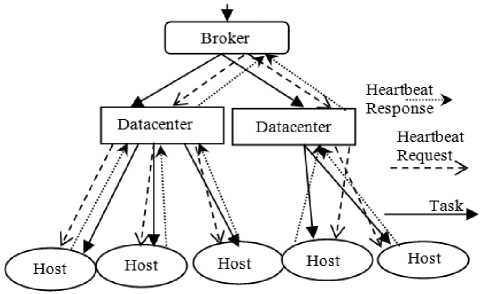
Fig.2. System Architecture

• IV.    The Analytical Model

The proposed algorithm considers mixed multiclass queuing network [5] to estimate communication latency. The queue size at one level affects the queue size at the next level in a multiplicative manner and thus we have considered product form network. There are two types of tasks, one with an exponential arrival rate and the other continue to circulate in the network in order to establish a mixed network model. The performance parameters are computed by BCMP theorem using Mean Value Analysis (MVA) [23]. The waiting and response time values have been used to estimate task completion time as in [24]. However, our system is crash recovery type, the factors like traffic burst and network congestion, may adversely affect the system performance. The waiting duration at broker includes host recovery time too. Fig. 3 demonstrates host recovery in machine repairman model.

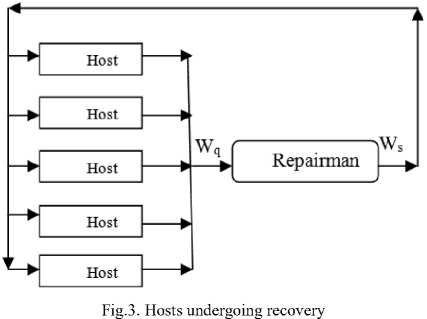
Table 1 depicts the symbols with their semantics that have been used in our illustration.

Table 1. Symbol Definitions

Symbols	Semantics
λ	Average arrival rate of transactions
S ck	Service time per visit of customer of class c at node k
V c k	Average no of visits of customer of class c at node k
D ck	Service demand of type c at node k
ρ ck	Utilisation of node k by class c
N=(N 1 ,N 2 ,….N C )	Overall population
W	Mean response time
L	Average number of customers
C	Closed class of customers
O	Open class customers

The utilisation of server by each customer job is obtained as follows:

• i.    For every host k :

Pck = ЯcDck , for all c e {O}(1)

• ii.    Service demand of heartbeat for host k

Dck = Dck I (1 - P{O},k )

• iii.    The response time of a heartbeat at host k ,

W. [n]= Dck [1 + Lk[n -1C ]]

• iv.    The response time of a particular class c :

Wc [ n ] = Zk=1 toK Wck [ n ]

The above computed response time is valid in a failure free run of the system. However, in the event of failure, recovery time too is taken into account for timeout calculation. Though, the recovery enhances overall system performance, it increases latency. Thus, a task operating on a recovery node would require larger duration for completion as compared to a task allocated to non-recovery node. Therefore, job completion time involves failure duration, recovery interval, and the time required to execute all queued jobs. The recovery time is computed using machine repairman model. The repair time at Repairman is the time required for host recovery. Table 2 describes the semantics of symbols used in the machine repairman model.

Table 2. Symbol Definitions

Symbols	Meaning
M	Mean time to failure
K	Number of hosts
W r	Time spent in repair
W q	Time spent in queue for repair
W s	Time spent in service

The repairman utilisation factor ( ρ) and arrival rate ( λ) is given by:

p = 1 - p о = B [ K , z ]               (5)

Я = p I W s                 (6)

where, B[K, z] is Erlang’s loss formula , z= M/W s

The arrival rate at repairman is used to compute cumulative waiting time at repairman, which includes mean time to failure, waiting time before repair, and service time to repair. It can be computed as follows:

Average arrival rate:

Я = KI (M + Wq + Ws)

Since,

Wr = Wq + Ws(8)

Thus ,

Wr =(KI Я)-M(9)

The repairman waiting time value obtained from eq (8) is recovery interval considered in case of failure and subsequent recovery. Therefore, the new timeout in case of recovery would be computed as follows:

T new = 2 W c + W r              (10)

where, W c is the value obtained from eq (4) for closed class of jobs (i.e. heartbeat).

• V.    The Algorithm Concept

A recoverable node could be in any of the three states: working, failed and recovering. After every timeout interval, non-responding node is added to suspected list. The timeout here is twice of response time for heartbeats considering maximum possible message propagation latency. A node once detected as failed is inserted in the suspected list till expiry of recovery interval. Each node in suspected list is checked for possible recovery. The recovered nodes are added in the list of working nodes and heartbeats are resumed. Thus, the total detection latency in crash recovery system is sum of timeout interval and recovery interval. Furthermore, once a node is suspected, no task is allocated to it until its revival. This improvises accuracy in being able to tolerate larger delay. Nevertheless, the node is detected crashed, in case, there is any further delay in the execution. Meanwhile, the system snapshots are taken at the interval same as the mean time between failures so that on occurrence of crash, execution resumes from the state just before the crash point. The broker reschedules the tasks that were scheduled initially on a node that was suspected later. Table 3 describes the events and functions used in proposed algorithm.

Table 3. Events/Functions used in algorithm

Function/Events	Description
initialise_ host(h);	Create hosts with provided specifications.
add(h->host_list);	Create a list of hosts available with each datacenter.
mount_vm();	Mount VMs on hosts available.
job_creation;	Create tasks according to arrival rate of tasks.
initialise_datacenter	Event sent from broker to datacenter to initiate execution
assign_task(c)	Assign task to VMs for execution according to space shared policy.
add(c->task_list)	Create a list of tasks to be executed by the system.
allocate_heartbeat(h)	Schedule one heartbeat at each of the tasks.
check_progress()	Checks the progress of the heartbeat at each of the host.
update_pulse	Sends an event to broker to update about status of each heartbeat.
update_pulse	Sends an event to broker to update about status of suspected node.
check_pulse()	Sends an event from broker to datacenter to query about the status of heartbeat progress.
check_crash()	Sends an event from broker to datacenter to query about the status of heartbeat progress in a suspected node .
check_task_status()	Returns the status of the tasks allocated.
task_replication()	Event sent from broker to datacenter upon timeout to take snapshot of task state still running on system.
replicate_task();	Pending tasks after a given timeout are replicated and scheduled by the broker.
add(h->suspect_list);	The detected nodes are enlisted in the suspected category upon timeout.
suspect_count(h)	List to maintain count of suspected nodes.
add(h->crashed_list);	List of crashed nodes is updated after recovery interval.
crashed_count(h)	List to maintain count of crashed nodes.
stop_execution();	Detection is stopped when either all tasks are completed or all hosts have failed.

• VI.    Algorithm

• A.    Algorithm for broker node

The proposed algorithm for failure detection considering possible recovery at broker node is as follows:

Initiate computation:

initialise_datacenter();

Periodic job_creation event:

for every unit time interval assign_task(c);

add(c->task_list);

Heartbeat creation:

for every host h allocate_heartbeat(h);// one cloudlet is created for each host//

Periodic detection event:

After every timeout interval delay for every host h check_pulse();

task_replication();

On receiving update_pulse event:

if (pulse_status!=SUCCESS) add(h->suspect_list); suspect_count(h)=suspect_count(h)++;

if (pulse_status==SUCCESS) remove(h->suspect_list);

After every recovery interval delay:

for every host h check_crash();

On receiving update_crash event:

if (pulse_status!=SUCCESS& h ε suspect_list) add(h->crashed_list);

• crashed_count= crashed_count++;

if(crashed_count(h)>number_of_hosts) abort();

// Completion// if (crashed_list==host_list ) stop_execution();

else

• for every c ε task_list if (task_status==Success ) stop_execution();

• B.    Algorithm for datacenter node

Algorithm for failure detection considering possible recovery at datacenter node is as follows:

Upon Receivinginitialise_datacenter:

initialise_ host(h);

add(h->host_list);

mount_vm();

job_creation;

After every periodic interval :

inject_fault();//(considering mean failure distribution)

On receiving check_pulse event:

check_progress();

update_pulse;

On receiving check_crash event:

check_progress();

update_crash;

On receiving task_replication event:

for every task c check_task_status();

if(task_status!=SUCCESS)

replicate_task();

• VII.    Experimental Setup

The above mentioned analytical model was computed for the following set of values provided in Table 4.

Table 4. Simulation values

Hosts	10	50	100
λ	10	50	100
N C	10	50	100
D o	0.05	0.01	0.005
D c	0.5	0.1	0.05
Parameters required for Recovery
M	72s	360s	720s
W s	10s	10s	10s

Using above values, the following performance parameters are computed:

• i.    Response time for heartbeat using eq (4).

• ii.    In case of a crash followed by recovery, total time spent in recovery is computed using eq (8).

• iii.    From above calculated parameters, timeout value in case of a crash followed by recovery is computed from eq.(10).

The proposed model is implemented using CloudSim plus [25], which is an event driven tool and closely resembles distributed computing environment. Table 5 briefly describes basic terminologies used in our simulation:

Table 5. Basic Terms

Terms	Functionality
Broker	Resource management entity. Initiates tasks into the system.
Datacenter	Entity responsible for working of physical hosts.
Host	Execution node where tasks are performed.
VM	Virtualization level to emulate resource scaling.
Cloudlet	Task to be executed by the system.

Following fig. 4 depicts the actual time of crash along with the detected time for 10 hosts.

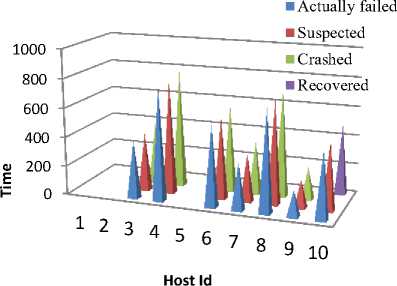
Fig.4. Detection time for each host

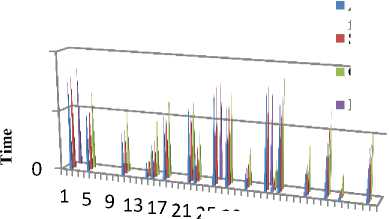
Blue cones in fig.4 represents time of occurrence of failure, red indicates time when they are suspected, green cones are for time of crash declaration whereas violet ones are to indicate recovery. As is evident from fig. 4 there are no cases of false detection or missed detection, since a blue cone precedes the red and green ones in all the cases. Thus, ensuring that a failure is detected, in case, it occurs. Further, the proposed algorithm has been simulated when scaled to 50 and then 100 hosts. It has been observed that completeness and accuracy is preserved even after scaling of resources. Fig. 5 and fig. 6 illustrates the simulation results for 50 and 100 hosts respectively. The occurrence of blue cones before red and red cones before green in fig.5. and fig.6. indicates the sequence of detection mechanism. Hence, a node is suspected when failure occurs and is declared crashed only if it fails to respond within timeout interval. Thus, our algorithm satisfies preliminary requirements of accuracy and completeness that is essential for any failure detection mechanism.

Fig.5. Detection time for 50 hosts

rashed

Actually failed Suspected

Recovered

Host Id

■ Actually failed

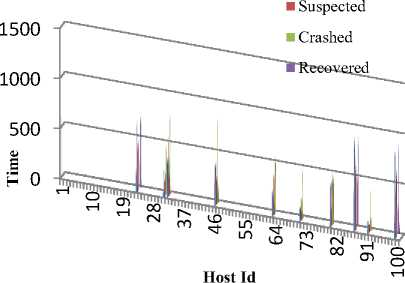
Fig.6. Detection time for 100 hosts

• VIII. Conclusion

The proposed algorithm considers failure detection problem in crash recoverable cloud nodes. We have abstracted the recovery part though it uses an underlying checkpointing mechanism. In simulation, we assumed jobs having common service requirement however it can also handle jobs with diverse service needs because we have considered mixed multiclass BCMP networks during experimentation. Secondly, in BCMP networks, the response time does not merely reflect detection latency rather it also includes recovery interval. Therefore, our time out calculation is more realistic as well as methodical and more importantly its value is minimal. The algorithm satisfies safety as well as liveness requirements. Our simulation results confirm that there is no false detection. Furthermore, the latency beyond timeout guarantees truthful fault detection. However, the impact of inexplicable traffic burst on the precise fault detection needs further investigation.