A Fast Topological Parallel Algorithm for Traversing Large Datasets

Big data is being produced at an unprecedented pace. Sorting a large volume of data or clustering it according to some criteria are a common operation used to extract information from it. Some recent application examples are ranking and recommending colleges through handling collected preferences [1], identifying internal relationships among telecom operators’ data assets [2], and processing data for supply chain improvements [3]. Graphs are probably the most widely used data structure for modeling big data problems and implementing algorithms to solve them. In general, the challenge is to generate a graph structure that represents a real scenario covering a large volume of data. A variety of strategies addressing the generation of such a data structure have been proposed. However, most of them are described at a high level and all related steps are superficially detailed. Therefore, these approaches lack reproducibility, which, in turn, makes the comparison between them an unfeasible task.

Regarding this scenario, the Algorithm for Generating Neighborhoods (ANG) presented by [4] arose as a pragmatic proposal for the generation of graph structures from large data sets. The authors validated the novel approach by using it to solve instances of the well-known Word Morph or Word Ladder game. The word morph game revolves around a dataset (or dictionary) of words and other two additional words w 1 and w 2 ; all words belonging to the problem instance are of the same length. The challenge is to find a sequence of words (ladder) from w 1 to w 2 such that each successor differs in only one letter from the predecessor. All successors must be taken from the supplied dataset [5]. Figure I. shows some examples of feasible solutions for the word pairs (BOY, PER), (CAR, SHY), (AXE, NUT), and (TRY, POT). Note that all intermediate words are assumed to exist in a dataset used to solve problem instances. In addition, the solutions presented correspond to one of many possible solutions.

Even though a central feature of the ANG algorithm is the complete generation of graphs from large data sets, in real scenarios this task may be unnecessary or not supported by the available computational resources. In other words, the problem instance in focus might only require a partial graph construction, or the entire graph might not fit in main memory. Furthermore, it is worth mentioning that the CPU time required to generate a complete graph can be such that the use of the underlying algorithm becomes unfeasible. In cases like these, the serial ANG algorithm may not be the most suitable approach.

The systematic way that the ANG algorithm was described in [4] made its proposal computational strategy possible to be reproduced. Therefore, in this work, the original algorithm was reimplemented followed by the implementation of a proposed new one. Thus, both algorithms could be compared under the same computational conditions. Like serial ANG, the new algorithm was tested on instances of the word morph problem. The main contributions of this work are:

• •    A novel parallel algorithm based on the approach employed by the ANG algorithm.

• •    The limitation of the ANG algorithm in relation to the complete construction of the graph was addressed. In effect, the graph induced by the new algorithm is partially assembled in memory – only the structure necessary for solving each problem instance is built. Such a change significantly improved memory usage.

• •  The parallel model employed in the proposed algorithm caused an outstanding CPU time improvement.

• •    Considering the need to sort a complete dataset, the algorithm can be easily modified to build a whole graph.

  BOY - PER	CAR - SHY	AXE - NUT	TRY - POT
  BOY	CAR	AXE	TRY
  BAY	CAT	1 APE	TOY
  BAT	PAT	ACE	TON
  CAT	PET	ACT	TIN
  CAR	SET	ANT	SIN
  PAR	SEE	AND	SIT
  	SHE	AID	PIT
  PER	1	BID
  	SHY	BIT	POT
  		POT

2.    Related Works 3.    Serial ANG

Fig.1. Word Morph Instances.

The rest of this paper is organized as follow. The next section reviews the literature related to finding graph structures for specific datasets. Section III details the serial ANG algorithm. Section IV is dedicated to describe all implementation of the parallel ANG. In the last two sections, the main results are presented followed by conclusions and future work.

Most of the strategies used to generate graph structures for data sets employ statistical methods. A typical way of classifying them is taking into account the randomness adopted in the graph structure generation, that is, if it is random or non-random. Regarding the random methods, the results obtained by [6] in the study of the small-world phenomenon have been explored in the modeling of graph structures for a variety of real networks. This is the case of [7] who studied the search for data in large information networks and [8, 9] who analyzed the small-world problem as an intrinsic characteristic of any type of network. The concept of topology was also explored by [10] in the construction of random graphs for collections of textual documents.

The second category of strategies to generate graph structures, i. e., non-random methods, have been found to be more useful for both theoretical and practical purposes. An example is the recursive matrix model proposed by [11] that can generate realistic graphs efficiently. Other network topology models were explored by [12] who applied them to generate graph structures for backbone networks. The online probabilistic topological mapping proposed by [13] also represented a relevant advance in the problem of finding the graph structure of an environment from a sequence of measurements.

The serial algorithm proposed by [4] is composed of three main steps:

• •    A relation is built between each pair of elements from a supplied dataset.

• •    A graph is built from the relations identified in the previous step.

• •    Topological neighborhoods are built based on an analysis conducted over the constructed graph.

Since the algorithm was fundamentally applied for solving word morph problems, the Levenshtein distance was employed to describe the relation pointed out in the first step. According to [14], the Levenshtein distance between two strings is the minimum number of character changes, insertions, and deletions required to transform one string into the other. Considering that the scope of the problems addressed by the ANG algorithm authors involves words with the same number of letters, the relation R between two elements (words) w 1 and w 2 was described as R ( w 1 , w 2 ): L ( w 1 , w 2 ) =

1, where L corresponds to the Levenshtein distance.

The second core concept explored by the algorithm is the graph whose structure is derived from the relation identified among the elements. Based on this premise, the following translation is carried out:

• •  Each word wi of the supplied dataset is treated as a vertice of the graph;

• •   There will exist an edge between two vertices wi and wj if, only if, the relation R(wi, wj) is verified.

4.    Parallel ANG

The last step of the algorithm explores the concept of vertex neighborhood. For each vertex (word) v i of the built graph G (dataset), its neighborhood N i corresponds to all vertices v ij directly connected to it. More formally

^i ⁼ {^(i+D) ^ С|Л(р,,У₀₊₁₎₇) ⁼ 1}                                 (1)

where j = {1, 2, ..., | N i |} and λ is the Levenshtein distance.

By applying the ANG algorithm to the Word Morph problem, it actually constructs the shortest path from the initial word to the target word. To ensure that cycles are eliminated during the dataset traversal process, Serial ANG organizes the generated neighborhoods into levels. This topological structure has a direct impact on the selection of elements that will compose each neighborhood. In fact, considering the neighborhood N i of a vertex v i , the neighborhood N i+1 is defined as

N_m = {^v(i+l)y G G|4^vi’ ^v(i+l)j) = ^{1 and v}(i+l); ^ ^NjJ ^ i}                     (2)

Based on the same concepts as Serial ANG, its parallel version has been proposed. Parallel ANG preserves the original neighborhood definition as well as the way they are arranged in levels. By using structures that implement these concepts, the new algorithm also generates the shortest path between a pair of vertices and does not create cycles in the associated graph. The core strategy of the algorithm relies on the producer-consumer paradigm [15]. The paradigm proposes that a parent process called the producer works on the input information and generates outputs that will be submitted to the child process known as the consumer. The consumer, in turn, will work with the information received and then generate results that will be transferred to the next consumer in the producer-consumer chain. Following this strategy, the intermediary processes play both the roles of consumers and producers.

Based on Flynn’s Taxonomy, that paradigm was implemented in a Multiple Instruction Stream – Multiple Data Stream (MIMD) architecture [16]. More precisely, a shared-memory system with multi-core core processors was employed to model the parallelism of the ANG algorithm [17]. The main idea involves using threads for acting as consumers or producers at each level of the topological structure structure induced during the traversal of the graph. Figure 2 sketches how such a paradigm was tailored to the algorithm dynamics.

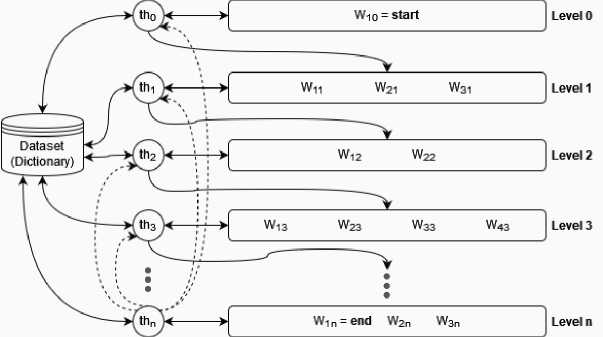
Fig.2. Parallel ANG Producer-consumer Schema.

The first thread ( th 0 ) is assigned to the first level (level 0) which is responsible for starting the algorithm operation, that is, the producer-consumer chain. As this level holds only the start word of the problem instance, th 0 plays the producer role for the next level which is under the responsibility of another thread ( th 1 ). Thread th 0 searches the dataset or dictionary for all words whose Levenshtein distance from the start words is equal to 1; the result of this searching corresponds to the production of th 0 . Note that as soon as a word is returned by th 0 search, it is immediately pushed to the next level. On the other words, th 0 produces a stream of words that differ from the words belonging to its own level

(only one word - the start word - in the case of level 0) by just one letter.

A thread finishes processing the level under its responsibility when there are no more words in the dataset differing just one letter in comparison to any word in the level. In this case, the thread is allocated to the next available level. It is worth mentioning that a control has been implemented to ensure that each word in the dataset is used only once. Consequently, the algorithm also does not build cycles. When any thread (at any level) hits the end word, it notifies all other threads. This causes the producer-consumer chain to be interrupted. In Figure 2, this broadcasting (represented by the dashed arrows) is triggered by thread th n .

On the other hand, if there is no a path between the start and end words, that is, there is no solution for the word ladder instance, thus the threads will process each level exhaustively. This scenario corresponds to one of the worst cases of the algorithm. The other one is when there is a path between the given words and each intermediate word of that path corresponds to the last word processed by the thread at its respective level. In Figure 2, this last scenario would be represented by the path { w 10 , w 31 , w 22 , w 43 , . . . , w 3n = end }, i. e., each last word of each level composing the path from start word to end word. Naturally, the best case happens when the first word of each level corresponds to a step of the path that connects the given words.

Figure 3 details an example of how the parallel ANG algorithm works. It builds a path between the amber and urges words. Three threads are responsible for processing the words at each level - subscript indices indicate the threads ID. The processing flow can be followed through the clock cycles represented by superscript indices. Hence, the arrow label th^m represents a thread whose ID is n that is processing a word in the m clock cycle. For example, th ⁴ indicates that thread 2 is processing a word in clock cycle 4. The dashed arrows describe all unsuccessful attempts to find the target word. The path between the given words is indicated by the sequence of solid arrows.

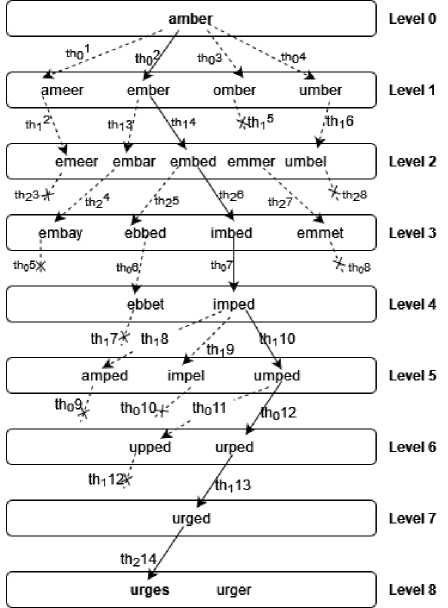
Fig.3. Example of Parallel ANG Working.

As shown by Figure 3, the word ladder instance was solved with an 8-step path - {amber, ember, embed, imbed, imped, umped, urped, urged, urges}. The solution was found after 14 clock cycles and was reached by thread 2. Note that, in this case, the broadcast triggered by this thread had no effect on the producer-consumer chain as there was no pending work in progress.

The proposed approach is detailed more precisely by algorithm 1 (Fig. 4.). It uses a set of additional structures (arrays) to control how threads process words per level (lines 2-6). The broadcasting mechanism is implemented by a shared variable (found) that is set when a thread hits the target word (lines 26-29). The threads’ work distribution in levels is managed by the array wlevel that holds the level each word belongs to. Basically, each thread goes through this array continuously looking for words whose associated level corresponds to the one it is responsible for. In addition to this condition, before processing a word, a thread also checks if that word has not been used by another one. Both conditions are verified in line 21.

Algorithm 1 Parallel ANG
Input: Dictionary diet. Word start, Word end
Output: Boolean found. List wlevel
1:	size = dict.length;
2:	notified[0:size] = false;
3:	notified[0] = true;
4:	wlevel |0:size] = infinity;
5:	wlevel [start.index] = 0;
6:	visited[O:size] = false;
7:	found = false;
8:	level = lastJevel =0;
9:	for 0 .. num.threads {
10:	thread_has_work = true;
II:	while not found and thread_has_work {
12:	atomic thlevel = level++;
13:	if thlevel > size {
14:	thread-has-work = false;
15:	continue;
16:	}
17:	last-check = false;
IS:	while not notified!thlevel] or not last-check {
19:	if notified[thlevel] { last-check = true; }
20:	for idL: 0 .. size {
21:	if wlevel[idL] != thlevel or visited[idL]
22:	next;
23:	for idLL: 0 .. size {
24:	if wlevel[idLL] < thlevel { next; }
25:	if is,ldiff(dict[idL], dict[idLL]) {
26:	if dictionary[idLL] == end {
27:	found = true:
28:	lastJevel = thlevel + 1;
29:	}
30:	wlevel[idLL] = thlevel + 1;
31:	visited[ idLL] = false;
32:	} }
33:	visited|idL] = true;
34:	} }
35:	if thlevel + 1 < size {
36:	notified[thlevel 4- 1] = true:
37:	} } }
38:	return (found, wlevel);

Fig.4. Parallel ANG Algorithm.

Algorithm 2 Ladder Extractor

Input: Dictionary diet. Word start, Word end, List wlevel

Output: List ladder

• 1:    lastJevel = get JastJevel( wlevel);

• 2:    ladder[O:lastJevel + 1] = 0;

• 3:    ladder[last Jevel] = end;

• 4:    lastJevel -= 1;

• 5:    for level: last-level.. 0 {

• 6:     for id : 0 .. dict.length {

• 7:        if wlevel[id] = level {

• 8:              if is_ldiff(ladder[level + 1], dict[id]) {

• 9:                  ladder[level] = dict[id];

• 10:                break:

• ¹¹    } } } }

• 12:    return ladder;

5.    Results

Fig.5. Ladder Extractor.

The algorithm generates a topological data structure that relies on another additional procedure (Algorithm 2 – Fig. 5.) to assemble the solution. This algorithm uses the same wlevel array to map the words at each level to another array ( ladder ) that corresponds to the path connecting start and end words. Naturally, this procedure is invoked only if a solution was found by the parallel ANG algorithm.

Both the original ANG algorithm and the parallel algorithm proposed by this work were coded in the Rust programming language - version 1.48.0. The experiments were performed on a PC running Ubuntu Linux operating system, version 14.04.5 LTS, with Kernel version 3.19.0-31. It consists of one Intel i7-3610QM processor of 4 cores (two threads per core), operating at 2.3 GHz. Each core has a unified 256KB L2 cache and each processor has a shared 6MB L3 cache. The PC contains 8GB of main memory. The complete source code is available on GitHub repository [18]. The word ladder instances were adapted from an academic material produced for advanced programming assignments [19]. The dictionary consists of 183,719 words and each of the 23 test cases corresponds to word pairs ranging from 4 to 9 letters. Both the dictionary and test cases are also available on GitHub repository [18]. Thus, the accuracy and reliability of the results presented can be verified by cloning the repository and running the project.

As detailed in Table 1, the parallel ANG achieved outstanding results considering the CPU time. In fact, the proposed algorithm presented better performance for 21 test cases and the improvement rate was from 10.12% (instance 7) up to 99.85% (instance 21). In all cases, both algorithms found the shortest path between the given words. Such a significant decrease in the time required for solving the test instances was expected, since the generation of the underlying graph is interrupted as soon as the optimal solution is reached. Note that this strategy was found to be efficient even for very small instances. It turns out that the additional cost related to instantiating and managing multiple threads is cheaper than going through the full graph construction. Another natural consequence is the reduced use of main memory given that only a narrow part of the graph must be stored.

Table 1. Results Comparison. The Steps Column shows the Number of Intermediate Words that Make up the Path between Start and End words. The Reduction Column Indicates the rate of CPU time Reduction Achieved by the Fastest Algorithm Compared to the other.

Input			Steps (#)	CPU Time (sec.)		Reduction (%)
#	Start	End		Serial	Parallel
01	monk	perl	5	0.340	0.394	13.71
02	slow	fast	5	0.366	0.248	21.31
03	blue	pink	5	0.316	0.417	24.22
04	stone	money	9	1.520	1.279	15.86
05	money	smart	9	1.546	1.270	17.85
06	devil	angel	8	1.483	1.076	27.44
07	atlas	zebra	11	1.552	1.395	10.12
08	babes	child	8	1.526	1.311	14.09
09	mumbo	ghost	9	1.516	1.335	11.94
10	train	bikes	9	1.513	1.080	28.62
11	babies	sleepy	13	4.809	2.209	50.47
12	charge	comedo	20	5.551	2.560	53.88
13	boyich	painch	31	6.916	2.501	63.84
14	brewing	whiskey	21	11.749	2.263	80.74
15	chantry	swither	7	11.563	0.389	96.63
16	postman	bankers	8	11.498	0.449	96.09
17	careers	outline	12	11.603	1.918	83.47
18	dancers	leading	14	11.557	2.038	82.37
19	atlases	cabaret	41	11.683	3.320	71.58
20	quirking	wrathing	20	126.339	0.584	99.54
21	gestates	ravelled	7	56.410	0.087	99.85
22	creative	whacking	7	195.665	0.335	99.83
23	decanting	derailing	16	16.141	0.077	99.52

A significant speedup of the algorithm was also observed with the longest word pair, i. e., the 9-letter words (decanting, derailing). When running the algorithm with 4 threads, the best performance improvement (2.01X) was obtained in that instance. On the other hand, the use of a larger number of threads caused a degradation of the algorithm speedup. Such a result was expected since the tests were performed on a 4-core processor. All this behavior is graphically described in Figure 6.

Although speedup was constrained by computational resources - basically the number of processor cores – within the range of available cores this metric did not scale as one might suppose. In fact, from 2 to 4 threads the speedup rate was lower than the first interval. This might suggest some bottleneck in the algorithm that is constraining its scalability. Another aspect to note is that the algorithm did not take advantage of the hyper-threading feature available on the CPU. When using this feature, its performance was expected to speed up to 8 threads, which was not observed as mentioned earlier.

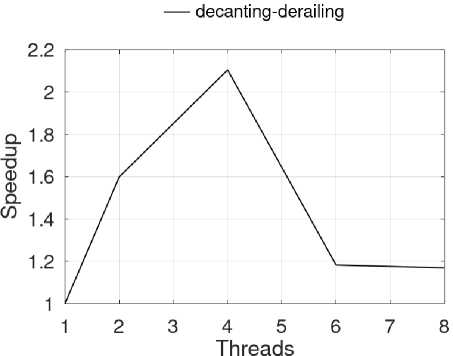
Fig.6. Speedup of Parallel ANG.

6.    Conclusion

This work presented a fast parallel algorithm based on the serial ANG algorithm designed to build graph structures from large data sets. The proposed strategy was demonstrated by applying it to the word ladder game. Addressing the intrinsic characteristic of the serial algorithm related to the construction of the complete structure of the graph, the new algorithm offers an efficient alternative when generating the graph on demand. More precisely, the parallel algorithm gradually builds the graph and stores it in main memory until the word ladder solution is found. In this way, this new strategy constitutes a more efficient approach regarding the use of computational resources. The achieved results also endorse the improvements related to CPU time. For the set of tested instances, the attained time reduction varies between 10.12% and 99.85%. Other significant results show the parallel ANG algorithm achieving speedups up to 2.01X with 4 threads. Considering the quality of the solutions, that is, the sequence of intermediate words separating two input words, the shortest path was also obtained by the parallel version of the algorithm. This means that the accuracy provided by the original algorithm was maintained.

As the topological approach presented by the serial ANG algorithm was also preserved, this new parallel version may be straightforwardly adapted to traverse large datasets. In fact, a significant next algorithm evaluation should involve a test of its performance to sort log files as proposed by the work [4]. Regarding the algorithm performance, it showed speedup improvements only up to 4 threads. Thus, another very important analysis to be performed is to submit it to a stricter profiling procedure. This approach can detect any bottlenecks that are limiting the scalability of its performance.