A Few Applications of Imprecise Matrices
Автор: Sahalad Borgoyary
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 8 vol.7, 2015 года.
Бесплатный доступ
This article introduces generalized form of extension definition of the Fuzzy set and its complement in the sense of reference function namely in imprecise set and its complement. Discuss Partial presence of element, Membership value of an imprecise number in the normal and subnormal imprecise numbers. Further on the basis of reference function define usual matrix into imprecise form with new notation. And with the help of maximum and minimum operators, obtain some new matrices like reducing imprecise matrices, complement of reducing imprecise matrix etc. Along with discuss some of the classical matrix properties which are hold good in the imprecise matrix also. Further bring out examples of application of the addition of imprecise matrices, subtraction of imprecise matrices etc. in the field of transportation problems.
Imprecise Number, Partial Presence, Membership Value, Imprecise Matrix, Reducing Imprecise Matrices, Imprecise Form
Короткий адрес: https://sciup.org/15010737
IDR: 15010737
Текст научной статьи A Few Applications of Imprecise Matrices
Published Online July 2015 in MECS
Two Classical set theories
Л П Лс = 0
and Л U Лс = 0 (1)
where 0 and 0 are empty and universal set respectively are not hold good in the definition of
Zadeh[1]. In the other word the universal set is the largest set of consideration set. Then how a one membership can be common in both the set and its complement set or why the union of membership and non membership set do not equal to universal set? We feel like there something is missing, because of that only it happen. The reason behind such a claim can be contributed to the fact of complement definition Zadeh for the fuzzy membership function defined by
( 1 - / i (x), when a < x < P
-
1 - / 2 to, whe n P < x < у (2)
0, о therwiee
By the help of this complement definition and the intersection and union of two fuzzy sets A and B defined by,
А П В = min{/i (x), /2(x)}, and (3)
A U В = max{/i (x), /2 (x)}, where /i (x) and /2 (x) are the membership functions of the fuzzy sets A and B really give rises to the result of intersection and union of fuzzy set and its complement is not a null set and the universal set respectively. In the universal graph composition of any classical set tells element of the complement part of the set never be included in the set and reversely the element of the set cannot be included in the complement of its set. In the same way we claim that membership functions of a set and its complement are not same that can be common in both the sets. On this fact the article bring up examples so that we can compare the complement definition of Zadeh and the extension definition called new complement definition of Baruah.
This definition has been developed by different individuals to bring up many papers and articles in the various field of mathematics since 1965. We claim that the problems which are solved by the complement definition of Zadeh occur error due to some partial element is skipped in the complement definition. So rectification would be done in the new complement definition of Baruah such that we can get more accurate result. Further to look into some practical problem in the field of transportation which is obtained in the form of Fuzzy matrices that can be written in the imprecise form by the help of definition of Baruah [2],[3],[4],[5], this article comes out.
The rest of article organized as follows: Section II deals with definition of imprecise number, normal imprecise number and its complement, partial presence, membership function, membership value. Section III deals with the definition of imprecise matrices, new matrix called reducing imprecise matrices, determinant, transpose, identity, null of imprecise matrices and their complement with applications and examples. Section IV deals arithmetic operations of imprecise matrices and their existence of properties and applications. Finally section V goes to the conclusion.
-
II. Definitions
The articles of Baruah [2], [3], [4], [5] explain how the definition of Zadeh violates the theory of union and intersection of classical set and Boolean algebra and justified them with counter examples and suggest to rectify it some partial element is necessary for inclusion and exclusion to the complement definition of Zadeh.
-
A. Imprecise Number : Imprecise number is a closed interval N = [ a, P,y] is divided into closed sub-intervals with the partial presence of element in both the intervals.
-
B. Partial presence: Partial presence of an element in an imprecise real number [ , , ] is described by the present level indicator function ( ) which is counted
from the reference function r(x) such that present level indicator for any x, a < x < y, is (p (x) — ( (x)) , where 0 < r(x) < p(x) < 1
-
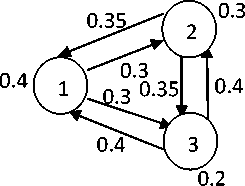
C. Membership value: If an imprecise number N = [ a, P, y] is associated with a presence level indicator function pv (x) , where
(pi to, Pn to = p 2 to, 0, when a < x < P when < < x With a constant reference function 0 in the entire real line. Where ( ) is continuous and non-decreasing in the interval [ , ] , and ( ) is a continuous and nonincreasing in the interval [ , ] with p( (a) = p 2(y) = 0, then ( ( ) — ( )) is called membership value of the indicator function ( ) D. Normal Imprecise Number: A normal imprecise number N = [a,P,y] is associated with a presence level indicator function ( ) , where (pi (x), PN to = P2 to, 0, when a < x < P when P < x < y о therw ise With a constant reference function 0 in the entire real line. Where ( ) is continuous and non-decreasing in the interval [ , ] and ( ) is a continuous and nonincreasing in the interval [ , ] with Pi (a) = p 2(y) = 0 Pi (P) = p (P ) = 1 (5) Here, the imprecise number would be characterized by {x, pv(x), 0 : x £ R} , R being the real line. For any real line, 0 < ( ) < ( ) < 1 normal and subnormal imprecise number will be characterized in common, {x,pi(x),p2(x): x £ R}, where p((x) is called membership function measured from the reference function ( ) and ( ( ) — ( )) is called the membership value of the indicator function. Here, the number is normal imprecise number when membership value of indicator function pv (x) is equal to 1 otherwise subnormal if not equal to 1. Moreover it can be said that the universal set if the membership value of pN (x) equal to 1 and null or empty set if equal to 0. E. Complement: For a normal imprecise number N= {x , pv (x), 0 : x £ R} as defined above, the complement Nc = {x,1,pv(x):x £ R will have constant presence level indicator function equal to 1, the reference function being pv(x) for —to< x < to Let us consider a curve defined in the closed universal set Q Where the universal set comprises of membership function p(x) and the non-membership functions ( ) and ( ) called membership value of the complementary function shown in the Fig.1. Membership function of the complementary function is measured from the level up to what the level of curve is occupied. Fig. 1. Complement of a normal fuzzy number Membership value and the membership function are not same in the imprecise form of definition. However both are same in the usual set. For this reason the intersection and union of imprecise form is defined in the following: Let A(p(,p() = {x, p((x), p2(x): xeQ} and В (p з ,p4) = {x,p ((x), p((x): xd}} be the two imprecise sets. Then the intersection and union is defined by, and A (p(,p() HB(p(,p4) _( x,min(p((x),p((x)), ) (max (p 2 (x), p4 (x)): xefiJ A(p(,p() U B(p3,p4) = ( x,max(p((x), p((x)), ) (min(p2 (x),p4(x)): xefiJ We claim that the theory of intersection and union of classical set are hold good by the definitions of imprecise number and its complement defined above. For this reason we consider a graph of surface having rectangular shape of dram filled with half portion of water. So the empty portion also becomes half. The filled of water and the empty portions are the membership value and reference value respectively. Here portion of dram filled with water is indicated by dark region and unfilled portion by white region. Fig. 2. Complement of Sub-normal imprecise number (a) Now according to Zadeh, membership value of the fuzzy set is A= ( and membership value of its complement set is So, Ac = 1 — = 2 2 A n Ac = min (1,1) = 1 which is a non-empty common region value of the fuzzy set and its complement set. And A U Ac = max Q,0 = | (not universal set) (9) That is the combine region of the fuzzy set and its complement set. But the inclusion of | empty portion in the set A and | fill portion in the complement of set Ac is meaningless as shown in the Fig.2. But according to the definition of imprecise set, {1,ц(РУц(а): 1 Е Д} = {1,1, 0:1 Е Д} and {1,H(^,H(Yy.1ER } = {Ц11ЕЙ} are the values of the imprecise set A(|,0) and the complement of imprecise set A(1,|) . So by the definition of union and intersection of imprecise set defined by Baruah we can obtained, A(1,o) П A (1,1) = {1, min (1,1), max = 21,-,-: 1 Е R}. L 2 2 J (o,2) : 1 Е Д which gives membership value. (1 — 1) =0 to form an empty set. And aG.0)u(1,|) = {1,max(-, 1),min(o, -) : 1 Е в! = {1,1,0: 1 Е Д}. (11) which gives membership value, 1-0=1 to form the universal set. Let us consider another example of dram of oil filled with 1 layer portion of oil. Since the oil floats on the water and the dram not full of oil. there will be 1 portion of dram as empty and 1 portion will be layer of water is shown in the following figure: Fig. 3. Complement of Sub-normal imprecise number (b) According to Zadeh, for the membership set or the fuzzy set A = {|,1}. the membership value of the layer of oil becomes _ 1 1 _ 1 =2-4=4 and the membership set of the complementary set is Ac = ((1 — j).(1 —j)} = {;,;}. which gives a membership value of the complementary set nothing but portion of the dram not filled with oil 3 11 ---= - 4 2 4 . This cannot be the membership value of the complementary set as the usual value must be (- + -) = -. 24/4 By the intersection and union definition of fuzzy set 11 1311 A n AC = (max(2,2),min(4,4)} = {2,4}. which is not a null set as the membership value does not equal to zero. And UA A =|min(?;),max(-,-)j = {?-}, which is not the universal set as the membership values is not equal to one. But according to the definition of imprecise number, the membership value of the imprecise set A (?;) = (1'?;:1ER} 11X1 is (---) = -. 2 4/4 That is filled with oil. And the portions not filled with oil are the imprecise sets and 4,2)= {ul^B} A(;.0) = (!•;• 0.1 ев} . which is shown in the Fig.3. Complementary part is the combination of both imprecise sets. So intersection of imprecise set and its complement are ■^ЭЧч) = (1,mln(i.1).max(i.l)} = (1.l.i.1EB} and a(|,>a(1o) = {1'mln(l'4)'max(4'o)'1ER} -U.^e») the Which gives membership value 0 and 0 to form empty set. Union of two empty sets is again empty. So the intersection becomes empty. By the associativity law of sets union of imprecise sets, Н?Эи л М))и (Л (?Эи л М) becomes, l,™^,!), Lmax^), I min(4’l):1eflJ Н4,0):1Ч = {1,1,1:1ед}и{1,|,0:1ед} = {1,1,0:1ед} (17) whose membership value is (1 — 0) = 1 to form a universal set. Further it can be verified that the following properties of classical sets are satisfied by the definition of imprecise sets A, B and C: (1) Idempotent Laws: (i) Л U Л = Л (ii) Л U Л = Л (2) Commutatively Laws: (i) Л U В = В U Л (ii) Л П В = В П Л (3) Associatively Laws: (i) Л U (S U C) = (Л U S) UC (ii) Л П (S П C) = (Л П S) ПC (4) Distributive Laws: (i) Л U (S П C) = (Л U S) П (S UC) (ii) Л П (S U C) = (Л П S) U (Л ПC) (5) De Morgan’s Law: (i) (Л U S)c = Лс П Bc (ii) (Л П S)c = ЛcUBc III. Imprecise Matrices It is concerned that many of our problems are in the form of matrix that has been discussed with the definition of classical matrices. But these are not overcome our real life problem as our day to day life problems are very much related with fuzzy concept. Matrix with real entries in [1, 0] and the matrix operations defined by fuzzy logical operations of reference functions are called imprecise matrices. All the imprecise matrices are classical matrix but every classical matrix are not imprecise matrix. Fuzzy matrices are first time introduced by Thomson who discussed more details in the Convergence of Power of Fuzzy Matrices [9]. Based on reference function Dhar has also proposed fuzzy matrices in the articles [6], [7], [8]. Here, all the elements of imprecise matrix are imprecise number and are measured form 0 and the elements of its compliment are measured from 1. Though the imprecise number is characterized by, {x, ^N(x), 0 : x £ Д}, for convenient of writing the elements of the imprecise matrix are written in the form of order pair Guy(x),0) , where ^ y(x) is the membership value, V x £ R and are individually imprecise number. A. Definition. For any square of matrix ran a12i 1^2. a22 J of order 2, an imprecise matrix would be represented and defined by Г( a. n0) (a. 2 ,0)1 ''(Л) l(a2.,0) (a2 2,0)J where all the elements of matrix are individually imprecise numbers having membership values measured from the reference function of value zero. So, imprecise matrix of order 2 is denoted by М(Л) = [(a^y, 0)]2x2 In general MQ4) = [(ay,0)]mxn is imprecise matrix of order m x n, where m and n are the row and column of the imprecise matrix respectively. Example- Suppose a bus is moving to provide daily necessary foods to the three different locations namely center 1, 2 and 3 respectively. Bus capacity of proving services are such a way that total 100% and when at the centre 1 is 40% ,then its capacity of services at the center 2 and 3 are 30% and 30%, when at the center 2 is 30%, then its capacity at the center 1 and 3 are 35% and 35%, when at the center 3 is 20% ,then its capacity at the center 1 and 2 are 40% and 40% respectively. Which nothing but a transportation problem and the conditions, allocation of services at the center 1, 2 and 3 are the square imprecise matrix of order 3. Here, a.. = 40% = 0.4 a. 2 = 30% = 0.3 a. 3 = 30% = 0.3 a2. = 35% = 0.35 a22 = 30% = 0.3 a23 = 35% = 0.35 a3. = 40% = 0.4 a32 = 40% = 0.4 a33 = 20% = 0.2 which are membership values of the indicator function at the centre 1, 2, and 3 are measured from the reference functions of value as 0. Thus the problem form the following imprecise matrix, (a. .,0) (a. 2,0) (a. 3,0) (a2.,0) (a2 2,0) (a23,0) (as .,0) (a3 2,0) (a, 3,0)J3X3 (0.4,0) (0.3,0) (0.3,0) (0.35,0) (0.3,0) (0.35,0) (20) (0.4,0) (0.4,0) (0.2,0) The logic proposed in the problem is an imprecise form of diagram showing only the part of membership functions at the centre 1, 2 and 3, which are measure from the reference functions of the centers. Graphically, Fig. 4. Imprecise matrix of order three. membership functions and the reference functions of each element of the matrix. C. Reducing Imprecise Matrices: Reducing into smaller form of imprecise matrix by making minimum of all the elements of the matrix with respect to least element of that matrix is known as reducing matrix. It would be represented and defined by, Red.(М(Л)) = (min(av,aki), max0v,rki)) . Here the values of each path in the figure are the membership values of the difference between membership functions and the reference functions of each element of the matrix. B. Definition: The complement of an imprecise matrix И (Л) - [(aw,0)]mx„ of order mAn would be represented and defined by М= (Л) = [(1,а11)]тхп, (21) where all the elements of complement of imprecise matrix are individually imprecise number measured from 1(one). For example M_ [(I,0-7) (l,0-5)l М (S) = [(1,0.3) (1,0.4)] is the complement of imprecise matrix of M(A) = [ (0-7,0) ^'^l (22) М(Л) [(0.3,0) (0.4,0)], (22) Which may be explained when a bus has not capable of providing service 70% at the center 1, there is 50% chances at the center 2. Similarly if bus not provides service at the center 1 is 30%, their chance at the centre 2 is 40%, where the conditions and the allocations of the center 1nd 2 are imprecise form of square matrix of order 2. The values of the allocations or the elements of the imprecise matrix are the membership value of the imprecise number measured from the reference function of value 0 and the membership value of the complement imprecise matrix is measured from the reference function of value 1.Graphically, Where akl and rkl are the smallest membership and reference functions of the imprecise matrix М(Л) respectively, (0.4,0) (0.3,0)! Example- If М(Л) [(0.5,0) (0.2,0)] Red (М(Л)) So, (1,0.2) [(1,0.2) D. 0.7 "f min(0.4,0.2)J fmin(0.3,0.2)/T max(0,0) max(0,0) f min(0.5,0.2)J 0 max(0,0) (0.2,0) (0.2,0) [(0.2,0) 0.2,0 ] its reducing (1,0.2) (1,0.2)] Multiplication of min(0.2,0.2)/ min(0,0) ■ [J imprecise becomes, Imprecise Multiplication of two imprecise matrices М(5) will be represented and defined by, Matrices: М(Л) and М(Л5) = {maxmin(aiy,&i7-) ,minmax(rzy, r'zy)},(25) Provided two matrices are conformable for multiplication and the symbols have their meaning as discuss above. (0.4,0) (0.3,0) If M( ) [(0.5,0) (0.2,0)] (0.5,0) (0.7,0) and М(5) - [(0.2,0) (0.2,0)] be the two imprecise matrices, then their multiplication is, 0.7 Fig. 5. Complement of imprecise matrix of order two. Fig. 6. Imprecise matrix of order two. Here, Fig.5. and Fig.6. are compliment to each other. And the values of each path in the figure are the membership values of the difference between { { min(0.4,0.5) , max(min(0.3,0.2). min(maX(m°m') max(0,0) М(Л5) ,\A ( (min(0.4,0.7),\ Al jj (ma^(min(0.3,0.2))J } I m^mmOSS') } max (min(0.5,0.2) A ) (max fmin(0.5,0.7) Л ( min(0.2,0.2) )' ( j ( min(0.2,0.2) )' / max(0,0),\ Г j /max(0,0)A min ( max(0,0) ) ) к min (max(0,0) ) . Г (0.4,0) (0.4,0) [(0.5,0) (0.5,0) E. Identity Imprecise Matrices: Multiplicative identity imprecise matrix will be represented and defined by, W)-^.,0)] , HLA II where if i = j, a;y = 1 and if i ^ j, a;y = 0 Example- Matrix, M(7) = [(^) (?'n)] L (0,0) (1,0)J is an identity of square imprecise matrix of order 2. F. Null Imprecise Matrix: Null matrix will be represented and defined by, M (0) = [(0,0)]mxn. (28) Example- Matrix, M(0) = [(^) (n,n)] (0,0) (0,0) is a null square matrix imprecise of order 2. G. Transpose of Imprecise Matrices: Transpose of imprecise matrix М(Л) = [(ay,0)]mxn would be represented and defined by (M(Л')) = [(ay/,0)]mxn . (29) Graphically, Det. (М(Л)) = ( min(max(aw a22), max(a2i, a^)); (. max(min(0,0), min(0,0)) Where max(a11,a22) and max(a21,a12) are not always equal, however for equal value of max can be expressed in common max (a11,a22, a21,a12 ) and the elements of determinant are the imprecise numbers measured from the reference function of value 0. Thus Determinant of imprecise matrix of order three is written by, Det. (М(Л)) = (a11,0) (a21,0) ( ,0) ( ,0) (,0) ( ,0) (,0) ( ,0) (,0) 0.6 Fig.7. Imprecise matrix of order two. 0.4 0.6 Fig. 8. Transpose of imprecise matrix. The figure shows that changes of directions of activity is the formation of transpose of an imprecise matrix, where the conditions and allocations at the center 1 and 2 are the imprecise form and the value of the elements are measured from the reference functions. And the values of each path in the figure are the membership values of the difference between membership functions and the reference functions of each element of the matrix. Thus it be obtained imprecise matrix, Г (0.6,0) (0,3,0)1 7 7 И) [(0.5,0) (0.4,0)] and the transpose of imprecise matrix, (0.6,0) (0.5,0) 77( ) [(0.3,0) (0.4,0)] () Fig.7. and Fig.8. are transpose to each other. H. Determinant of Imprecise Matrices: If ian a12, |a2i a22| is a determinant of order 2, then the determinant of imprecise matrix would be represented by, Det. (М(Л)) = |(ai^ (ai2,0)| I (a21,0) (a22,0)l and defined by and defined by, . ( ( )) = {( a11. min(max(a22, a33), max(a23, a32))), (0. max(min(0,0), min(0,0)))} - {(a12. min(max(a21, аз3), max(a23, аз 1))), (0. max(min(0,0), min(0,0)))} + {(a13. min(max(a21, аз 2), max(a2 2, аз 1))), (0. max((min(0,0), min(0,0)))}, (32) where final value of determinant can obtained taking maximum operator between two additive number and minimum operator between two subtractive numbers respectively. (0.3,0) (0.4,0) Example: If MM) = [(0.7,0) ,0-,,,,] be square matrix of order two, then (0.3,0) (0.4,0)| Det.(MG4))|(0.7,0) (0.2,0)| _ Сmin(max(0.3,0.2), max(0.4,0.7)),) max(min(0,0) , min(0,0)) = {min(0.3,0.7),max(0,0)} = (0.3,0), (33) which is an imprecise number of membership value 0.3 I. Proposition: Complement of imprecise matrix is again an imprecise matrix. Г 1 (0.2,0) (0.5,0)1 Example: If М(Л) [(0.9,0) (0.2,0)] be a square matrix of order 2, then its complement becomes M = [(1,0^) (1,0.5)1 (34) M (Л) [(1,0.9) (1,0.2)] (34) This is also an imprecise matrix of order two measured from the reference function of value 1. IV. Arithmetic Operations of Imprecise Matrices Arithmetic operations of imprecise matrix are the operations of addition, subtraction, multiplication and division. These operations are expressed by the maximum and minimum operators of fuzzy sets which are introduced by M. Z. Ragab and E.G. Emam in their article [11]. Here, also these are discussed with new notation and definition to obtain possible definition and their properties with applications so as to study easier. A. Addition: Addition of two imprecise matrices M(4) and M(B) would be denoted and defined by ( max( an, b ,■,) J M (A) + M(B)-\ / (,[, mm^pr ,)) provided M(4) and M(B) are conformable for addition i.e. they are in same type, Where ay , by and , are membership functions and reference functions of imprecise matrix ( ) and ( ) respectively. Thus the maximum possibility that can provide services by the two objects same at different locations is the resultant of sum of the two matrices. 1 (0.5,0) (0.4,0)! Example- If M(/l) [(0.з,0) (0.1,0)] . Г (0.2,0) (0.3,0)! and M(5) - [(0.3,0) (0.7,0)] then, M (Л) +M(B) max(0.5,0.2) [ min(0,0) max(0.3,0.3) min(0,0) , max(0. .4,0.3) , (0,0) ,! |max(0.1,0.7),! } { min0) J. (0.5,0) (0.4,0) [(0.3,0) (0.7,0) In physical significance, it is a transportation problem where two buses ( ) and ( ) are providing services at the same centre 1 and 2, in such a way that bus M(4) can provide service 40% at 2,when 50% at the centre 1 and 10% at 2, when 30% at the centre 1. Similarly bus M(B) can provide service 30% at 2 when 20% at the centre 1 and 70% at 2 when 30% at the centre 1. The maximum possibility of services at the centre 1 and 2 are 40% at 2 when 50% at 1 and 70% at 2 when30% at 1. B. Proposition: Addition of two imprecise matrices is commutative. (0.1,0) (0.2,0) Example-If M(4) [(0.3,0) (0.4,0)] and (0.2,0) (0.4,0) M(s) - [(0.3,0) (0.1,0)] then (0.2,0) (0.4,0) M(Л) + M(B) [(0.3,0) (0.4,0)] and (0.2,0) (0.4,0) M(B)+M(Л) [(0.3,0) (0.4,0)] So we have, M(Л) + M(B) - M(B) + MG4) (37) B. Proposition: Addition of complement of two imprecise matrices is commutative. Proof: That is to prove that if ( ) and ( ) are imprecise complement matrices of ( ) and ( ) , then Mc (Л) + M C(B)-MC(B)+M С(Л) (38) Since the complement of imprecise matrix is again a imprecise matrix. So by the proposition 4.1 commutativity law hold good. C. Substraction: Substraction of two imprecise matrices ( ) and ( ) would be defined by ( min( an, b ,■,) J M(Л)-m(b)-{ ,ij’ ijJ’[ ( max(rtj,r ij) J provided both the matrices are conformable for substraction. Where , and , are membership and reference functions of imprecise matrices ( ) and ( ) respectively. Thus the minimum possibility that can provide services by the two objects same at different locations is the resultant of subtraction of the two matrices. (0.2,0) (0.3,0) Example- If ( ) - [(0.4,0) (0.5,0)] (0.3,0) (0.4,0) and ( ) - [(0.2,0) (0.1,0)] then, M (Л) -M(B) "| min2,0! fmin(0. .3,0.4),!" max(0,0) (0,0) fmin4,0.2),! (min5,0.1),! max(0,0) max(0,0) (0.2,0) (0.3,0) [(0.2,0) (0.1,0)] (40) In physical significance, it is a transportation problem where two buses ( ) and ( ) are providing services at the same centre 1 and 2, in such a way that bus ( ) can provide service 30% at 2,when 20% at the centre 1 and 50% at 2, when 40% at the centre 1. Similarly bus ( ) can provide service 40% at 2 when 30% at the centre 1 and 10% at 2 when 20% at the centre 1. The minimum possibility of services at the centre 1 and 2 are 30% at 2 when 20% at 1 and 10% at 2 when20% at 1. D. Proposition: Subtraction of two imprecise matrices is commutative. (0.1,0) (0.2,0) Example - If M(4) [(0.3,0) (0.4,0)] (0.2,0) (0.4,0) and ( ) - [(0.3,0) (0.1,0)] then, MM)-M(S)-[(0^0) <^>] (.,) (.,) , Г (0-1,0) (0.2,0)! and М(В- М(А) - [(0.3,0) (0.1,0)] So we have, М(А) - М(В) - М(В) - М(А) F. Proposition: If МС(Л) and Mc(Ba are Complement of imprecise matrices М(Л) and М(В) , then Mc (А + В) -МС(А) + МС(А), (42) where МС(А + В) is complement of sum of two imprecise matrices. Example- If М(Л) (0.3,0) [(0.5,0) (0.4,0) (0.6,0)] and М (В) (0.2,0) [(0.3,0) (0.4,0) (0.3,0)] then, МС (Л) - (1,0.3) [(1,0.5) (1,0.4) (1,0.6)] and МС (В) - (1,0.2) [(1,0.3) (1,0.4) (1,0.3)] . . Г(0.3,0) (0.4,0)! And М(Л) +M(B)- [(0.5,0) (0.6,0)] M (1,0.3) (1,0.4)1 М (А + В)-[(1,0.5) (1,0.6)] (1,0.3) (1,0.4) ( )+ ( ) - [(1,0.5) (1,0.6)] So, МС(А + В) - МС(Л) + МС(Л) G. Proposition: If МС(Л) and / С(В) are Complement of imprecise matrices М(Л) and М(В), Then ( - ) - ( ) - ( ) where ( - ) is complement of difference of two imprecise matrices. (0.4,0) (0.3,0) Example- If ( ) - [(0.5,0) (0.2,0)] and (0.4,0) (0.5,0) М(в)-[(0.6,0) (0.7,0)] then, (1,0.4) (1,0.3) 7 М И) [(1,0.5) (1,0.2)] and (1,0.4) (1,0.5) М (В) - [(1,0.6) (1,0.7)] And (0.4,0) (0.3,0) М(Л) М(5) [(0.5,0) (0.2,0)] м с(а R)_[(1,0.4) (1,0.3)1 М (А-В)-[(1,0.5) (1,0.2)] (1,0.4) (1,0.3) ( )- ( ) - [(1,0.5) (1,0.2)] So we have МС (А - В) - МС (Л) - МС (Л) The definition of addition and subtraction of imprecise matrices are almost same with the definition of union and intersection of imprecise sets as are also defined in the form of maximum and minimum operators. (41) V. Conclusion Our real life problem is complex in nature. It is very much related with fuzziness. Imprecise form is the feasible definition of fuzziness. So, in this article definition of fuzzy concept and its complement are discussed in the imprecise form with examples. Various orders of imprecise matrices are expressed in the above with graphical representation. Arithmetic operations of matrix are defined by the maximum and minimum operators. And these operators are the main tools to obtain properties of the above mentioned imprecise matrices. Further applications of addition of two imprecise matrices, Subtraction of two imprecise matrices and their complement are also discussed in the field of transportation problems. Study of more dimensions of imprecise numbers is the future prospect of research. Acknowledgment The author would like to thanks the anonymous reviewers for their careful reading of this article and for their helpful comments which have improved this work.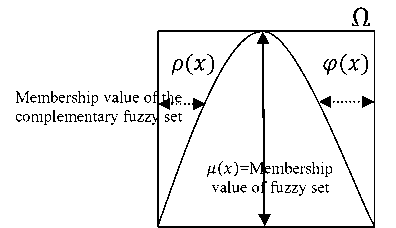


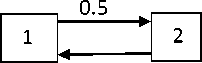


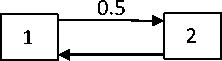
Список литературы A Few Applications of Imprecise Matrices
- L.A. Zadeh, Fuzzy sets, Inform. And Control, 1965, 8: 338-53
- H. K. Baruah, In Search of the Roots of fuzziness: The Measure meaning of Partial Presence, Annals of Fuzzy mathematics and Informatics, 2(1), 2011, 57-68
- H. K. Baruah., Theory of fuzzy sets: Beliefs and Realities, I. J. Energy Information and Communications. 2(2), (2011), 1-22
- H. K. Baruah., Construction of Membership Function of a Fuzzy Number, ICIC Express Letters 5(2), (2011), 545-549
- H. K. Baruah., An introduction Theory of Imprecise Sets: The Mathematics of partial presence, J. Math. Computer Science, 2(2), (2012), 110-124
- M. Dhar., Theory of Fuzzy Sets: An Overview, I.J. Information Engineering and Electronic Business, 2013, 3, 22-33
- M. Dhar, A Revisit to Probability- Possibility Consistency Principles, I.J. Intelligent Systems and Applications, 2013, 04, 90-99
- M. Dhar, A Note on Determinant and Adjoint of Fuzzy Square Matrix, I.J. Intelligent Systems and Applications, 2013, 05, 58-67
- M.G. Thomson, Convergence of Powers of a Fuzzy Matrix, J. Math. Anal. Appl., 57, 476-480. Elsevier, 1977
- J. B. Kim, Determinant Theory for Fuzzy and Boolean Matrices, Congressus Numerantium Utilitus Mathematica Pub. (1978), 273-276
- M. Z. Ragab and E.G. Emam, The determinant adjoint of a square fuzzy matrix, Fuzzy Sets and Systems, 61 (1994) 297-307
- M. Z. Ragab and E.G. Emam, On the min-max composition of fuzzy matrices, Fuzzy Sets and Systems , 75 (1995) 83-82
- L.J. Xin, controllable Fuzzy Matrices, Fuzzy Sets and Systems, 45, 1992, 313-319
- L.J. Xin, Convergence of Powers of Controllable Fuzzy Matrices, Fuzzy Sets and Systems, 63, 1994, 83-88
- T. J. Neog and D. K. Sut, An Introduction to the Theory of Imprecise soft sets, I.J. Intelligent Systems and Applications, 2012, 11, 75-83
- M. Dhar and H.K. Baruah, The Complement of Normal Fuzzy Numbers: An Exposition, I.J. Intelligent Systems and Applications, 2013, 08, 73-82.


