A Frequency Based Approach to Multi-Class Text Classification

Published Online May 2017 in MECS

Text classification, also referred to as text categorization, may be defined as the process of classifying textual information by means of its content. Due to the ubiquity of textual information, text classification finds application in a diverse array of domains such as text summarization, information extraction, information retrieval, question answering and sentiment analysis, to name a few.

Text classification is a form of text mining, which is a more general term used to denote any process that involves deriving information from textual data by analyzing patterns within it and is in turn a subset of the larger domain of data mining. Since in text classification, a labeled dataset is used to train the classifier, it is said that text classification is a supervised learning technique and differs from unsupervised learning techniques such as clustering where the training is performed using unlabeled data instances.

In this research paper, we have expanded on the work that was done in [1]. In [1], a binary text classifier had been proposed and implemented. It made use of an incremental approach to text mining wherein the newly classified data instances and their predicted labels were added to the existing training data set so that this enhanced data set could be used to train the classifier for predicting the labels of future unclassified data instances. This allowed for more thorough classifier training and increased classification accuracy each time the classifier was used for the same problem.

The motivation behind improving upon the previous work in [1] has been two-fold. First, the primary limitation of the previous classifier was that it could only perform binary classification. The classifier needed to be more dynamic and applicable in a wide variety of training sets. Additionally, a classifier shouldn’t constrain the data set to consist of a specific number of classes and should not inconvenience the users by having them supply the number of classes present in the training data since the users themselves may not be aware of this information. Second, it seemed that higher classification accuracy could be achieved by making certain optimizations to the existing algorithm and implementing the tf-idf (term frequency-inverse document frequency) statistic [2][18] in place of simple word frequency as was done in the binary classifier. In the following sections, it will be illustrated that both of the above-mentioned goals have been successfully achieved and a classifier has been developed accordingly. The new classifier is now capable of automatically inferring the number of classes in the training data while achieving higher classification accuracy.

The rest of the paper is structured as follows. Section 2 contains a short overview of related research work in the field of text classification and states a few examples of text classifiers implemented using different known techniques. Section 3 provides a detailed description of the theoretical principles and concepts behind the proposed text classifier. Section 4 offers a working description of the proposed classifier, stepping through the pseudocode and algorithms behind its implementation. Section 5 is a discussion of the time complexity of the classifier and contains an analysis of the results obtained using the classifier. Section 6 concludes the paper with a summary of the work and its future scope.

• II.    Related Work

As mentioned in the previous section, the work in this paper is an extension of our previous work in [1] where a simple binary text classifier had been implemented. That classifier made use of incremental mining and word frequency for classifying new instances. Various other methods of text classification and categorization exist and have been implemented using a variety of different techniques in various other research works.

The paper in [3] defines text categorization as “the task of automatically sorting a set of documents into categories (or classes, or topics) from a predefined set” and states that it falls under the domain of both machine learning and information retrieval. Thus, techniques derived from both of these domains find application in implementing text classifiers. Joachims [4] proposed the use of Support Vector Machines (SVMs) for text classification and demonstrated that SVMs could be more optimal than other machine learning methods such as k-NN classifiers and Naïve-Bayes classifiers. In [5], Cristianini discussed in great length the working principles and applications of SVMs in text classification.

Another popular variant of text classifiers is one based on Bayes’ theorem and referred to as the Naïve Bayes classifier. In [6], Leung defined Bayesian classifiers as statistical classifiers that are capable of predicting the probability of a specific test instance belonging to a specific class. Frank and Bouckaert [7] demonstrated the use of a variant of the Naïve Bayes classifier called the Multinomial Naïve Bayes (MNB) in solving problems of text classification pertaining to unbalanced datasets. Another variant of the Naïve Bayes text classifier is offered by Dai, Xue, Yang and Yu [8] in which they solved the problem of categorizing documents across varied distributions.

The k-Nearest Neighbors (k-NN) technique, as stated above, has also been used in the field of text classification. The k-NN algorithm finds the k nearest neighbors of the data instance that needs to be classified in order to form its neighborhood. Then, a voting mechanism is used within the neighborhood to determine the class of the instance. Guo et al. [9] developed a new method for text classification which combined the advantages of the k-NN algorithm with another type of classifier known as the Rocchio classifier and obtained performance levels in the range of that offered by SVM-based text classifiers. In [10], Toker and Kirmemis made use of the k-NN classifier to develop an application for organizing documents. Additionally, Li, Yu and Lu [11] developed a modified k-NN based method that utilized a suitable number of nearest neighbors in order to predict classes based on the distribution of a particular class in the test documents.

• III.    Theory Behind the Proposed Work

The property that has been incorporated into the present research work to help boost its accuracy is the inverse class frequency. This is based on the tf-idf (term frequency-inverse document frequency) statistic that is widely used in information retrieval. The tf-idf method helps in determining the importance of a particular term with respect to a specific document within a collection of documents and finds use as a weighting factor [2][18]. It is directly proportional to the term frequency which is the number of times the term appears in the document while being inversely proportional to the document frequency which is the number of different documents within the collection in which the term appears. Thus, tf-idf essentially combines two weighting factors based on the following two principles:

• 1.    The weight of a term within a document is proportional to the term frequency [16]

• 2.    The specificity of a term is inversely proportional to the number of different documents in which the term occurs [17]

To suit the purpose of our present research work, a similar property has been defined in this paper for each test instance and has been termed as the word frequency– inverse class frequency or wf-icf. As the name suggests, wf-icf is directly proportional to the word frequency which is the number of times a particular word in an instance appears in all the instances belonging to a particular class and is inversely proportional to the class frequency which is the number of different classes in whose instances the words making up the current instance appears.

The word frequency ‘wf’ is computed during the training phase by simply counting the number of occurrences of each word separately for each class. The ‘icf’ of each word ‘w’ in the instance is then computed during the classification phase using the following formula:

ICF (w) = log10 (N/M), where N is the total number of classes in the dataset and M is the number of classes which contains a specific word ‘w’ i.e. the number of classes for which wf(w) > 0. This formula has been taken from the formula used in the calculation of the tf-idf statistic.

In order to classify the test instance, the product of the word frequency of each word in each class and the inverse class frequency of each word making up that instance has been computed and then the products for each class have been summed up. This product is the wf-icf as defined above. After this, the instance is classified into the class which has the maximum value of this product sum.

To illustrate the above method, the task of classifying book titles into different subjects has been considered. Suppose we have five different subjects - Biology, Chemistry, Computer Science, Mathematics and Physics. After stop word removal and lower case conversion, let the test instance be ‘introduction java programming’. Table 1 shows the frequency counts for each word with respect to each class. From the table, the ICF would be as follows using the previously mentioned formula:

ICF (introduction) = 0.0969

ICF (java) = 0.6989

ICF (programming) = 0.221

Table 1. Word Frequencies

	Biology	Chemistry	Computer Science	Maths	Physics
Introduction	8	3	1	2	0
Java	1	0	2	0	0
Programming	0	0	4	2	1

Table 2. WF-ICF Values

	Biology	Chemistry	Computer Science	Maths	Physics
Introduction	0.78	0.29	0.1	0.19	0
Java	0.70	0	1.4	0	0
Programming	0	0	0.88	0.44	0.2

Each frequency count as shown in Table 1 is then multiplied with the ICF for the corresponding word to obtain the WF-ICF values as shown in Table 2.

The values in each column from Table 2 are then summed up. So each summation value shows the result corresponding to a particular class. With this, the following values are obtained:

Biology = 1.48

Chemistry = 0.29

Computer Science = 2.38

Math = 0.63

Physics = 0.2

Since Computer Science has the highest wf-icf value, the instance ‘introduction java programming’ will be classified as a Computer Science textbook which is of course the correct class. This result has been a major improvement on the previous classifier proposed in [1], where only the word frequency had been used to classify the instances. For example, since the previous classifier only used word frequency and did not incorporate the ICF property, it would have classified the above instance as a Biology textbook since the training dataset in the above example contains a larger number of Biology textbooks with the word ‘introduction’ in it. Being able to correctly classify such instances is what helped to boost the present classification accuracy while enhancing the classifier to be able to classify between any numbers of classes.

To develop a mathematical formulation for the present classifier, let the number of data classes in the training data be N, numbered from 0 to N-1. Let the current test data instance to be classified consist of W words, numbered from 0 to W – 1. Also, let the frequency count of each word in the training instances of a particular class be represented by WF(X,Y) where X is the word number and Y is the corresponding class number and the previously defined inverse class frequency of each word X be given by ICF(X). Thus,

X = {0, 1, 2… W-1} and Y = {0, 1, 2 … N-1}

The next step is to find a relation that specifies the conditions for a test data instance to be correctly classified. For this, let C be the class number of the current test data instance’s actual class label. Thus, the classifier will be correct if it predicts that the class label of the current test instance is class number C.

Based on the previously defined notation, for word number I of the current test data instance, the frequency of occurrence of that word in training instances belonging to class C in the training data set is given by WF(I,C). Additionally, the corresponding inverse class frequency is ICF(I). Thus, the wf-icf property is given by WF-ICF(I,C) where

WF-ICF(I,C) = WF(I,C) * ICF(I)

Thus, a test instance will be correctly classified if the summation of WF-ICF(I,C), for all words I of the test instance, is greater than the summation of WF-ICF(I,Y) for all the other N-1 classes, where Y is a class number ranging from 0 to N-1 but not equal to C. Thus, this can be mathematically represented as:

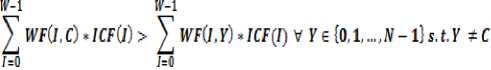
In the above expression, C is the class number of the actual class the test instance should be classified into, W is the number of words in the current test instance, Y is the class number of all classes except class number C, WF is the frequency count as defined previously and ICF is the inverse class frequency as defined previously.

• IV.    Work Description

In this section, an overview of the algorithms used to implement the initialization, training and testing phases of the multi-class incremental text classifier is presented. A brief description of each phase is given followed by the steps involved in implementing the phase.

In the initialization phase, the algorithm reads in the training data instances along with their corresponding class labels. It then counts the number of different classes contained in the training data set and also constructs the hash table which will store the mapping between the different words contained in the training data to the corresponding word frequencies. This mapping is performed in the training phase. The final step in the initialization phase involves pre-processing the training data for the training phase. The steps are outlined below.

• A.    Initialization Phase

• •    Read in training data and store in an array called ‘trainData’, with each element containing a training instance

• •    Read in corresponding class labels and store in an array called ‘labels’

• •    Loop through ‘labels’ to determine the number of different labels (i.e. classes) and store it in a variable called ‘N’

• •    Create a hash table called ‘wordList’ whose keys will be the words in the training data and the values will be the word counts

• •    Create a string array called ‘categories’ that stores the different class labels

• •    Convert each instance in ‘trainData’ to lower case

The training phase involves populating the hash table created in the initialization phase with the words contained in the training data and their corresponding frequencies. Thus, in this phase, the algorithm iterates through the training data instances, scans each word contained in these instances and updates the frequency counts stored in the hash table accordingly, depending on the class label of the data instance which the word is contained in. The steps for this phase are given below. The frequency of each word is stored as an array of N elements where N is the number of class labels contained in the training data set. The ith element of this array stores the number of times the corresponding word appears in training instances belonging to the ith class.

• B.    Training Phase

• •    Iterate through each member of ‘trainData’

• •    Store the corresponding label in a string called ‘trainLabel’

• •    Remove punctuation and the stop words for each instance

• •    Convert the resulting string of words into a string array

• •    Check if it is in ‘wordlist’ for each word in the array

• a)    If not, add it as a key in ‘wordList’ and set the value of that key to a list of ‘N’ elements of 0 but the i^th element set to 1 where the i^th class label is ‘trainLabel’

• b)    Otherwise, retrieve the list stored in the value field of the corresponding word and increment the i^th element by 1 where the i^th class label is

‘trainLabel’

The final phase is the testing phase in which the accuracy of the classifier is determined. In this phase, the algorithm reads in the test data instances and corresponding class labels and pre-processes them in a manner similar to what was done in the training phase. Then it predicts the class label of each test instance. In order to do so, for each test instance, the algorithm iterates through each of its constituent words, computes the wf-icf values for the word and each class label as defined in the previous section. It then sums the wf-icf values for each class label and selects the class label that maximizes this sum as the predicted class label. If this predicted label is the same as the actual class label, then the count of correct predictions is incremented. The process is continued for all test instances and the prediction accuracy of the classifier is determined using the final count of correct predictions.

• C.    Testing Phase

• •    Read in test data and store in an array called ‘testData’, similar to how the training data was stored

• •    Read in corresponding class labels and store in an array called ‘testLabels’

• •    Initialize a variable called ‘correct’ to 0 - this will store the total number of correct predictions

• •    Iterate through each member of ‘testData’

• •    Store corresponding label in a string called ‘testLabel’

• •    Convert to lower case, remove punctuations and stop words and convert to array for each instance

• •    Create an integer array called ‘sums’ consisting of N elements

• •    The i^th element of ‘sums’ will store the sum of the number of times the words in the current test instance appear in a training instance with the i^th class label

• •    Initialize a variable called ‘userCat’ to 0 – this will store the predicted label

• •    For each word in the array, check if the word is in the ‘wordList’ hash table which was constructed during the training phase

• a)    If not, nothing is to be done

• b)    Otherwise, retrieve the array stored in the corresponding value field and calculate the inverse class frequency using the formula defined in the previous section

• c)    Update ‘sums’ accordingly, i.e. calculate the product of the number in the i^th element of the value array and the inverse class frequency and add the product to the i^th element of ‘sums’. This product is the ‘wf-icf’ value that has been defined previously.

• •    Set the variable ‘userCat’ to the index in ‘sums’ that corresponds to the maximum value

• •    Increment ‘correct’ if the label corresponding to

‘userCat’ is the same as the corresponding label in ‘testLabels’

• •    Add the words of the current test instance along with the predicted label to ‘wordList’. This step implements incremental classification.

• •    Repeat the process for all remaining test instances

• •    Calculate the classifier accuracy using the ‘correct’ variable which stores the number of correct predictions.

• •    Finally, output the total number of test data instances, the number of correct predictions and the resulting prediction accuracy of the classifier.

• V.    Result and Analysis

In order to test the classifier, k-fold cross validation has been performed with k = 6 using a dataset consisting of a total of 300 book titles spanning 5 different subjects, viz., Biology, Chemistry, Computer Science, Mathematics and Physics with 60 titles of each of the subjects. In each step of cross validation, a hash table has been constructed thus giving a total of 6 hash tables. The order of the subjects used in constructing these tables is as given above. So, Biology comes first, followed by Chemistry, Computer Science and Mathematics in that order and finally, the last entry corresponds to Physics.

Table 3. The first five entries of the first hash table

Word	Subject-wise Count
inorganic	[0, 2, 0, 0, 0]
programmer	[0, 0, 1, 0, 0]
unity	[1, 0, 0, 0, 0]
repair	[1, 0, 0, 0, 0]
evolutionary	[1, 0, 0, 0, 0]

Table 4. The first five entries of the second hash table

Word	Subject-wise Count
inorganic	[0, 2, 0, 0, 0]
programmer	[0, 0, 2, 0, 0]
unity	[1, 0, 0, 0, 0]
repair	[1, 0, 0, 0, 0]
evolutionary	[2, 0, 0, 0, 0]

Table 5. The first five entries of the third hash table

Word	Subject-wise Count
inorganic	[0, 1, 0, 0, 0]
programmer	[0, 0, 2, 0, 0]
unity	[1, 0, 0, 0, 0]
evolutionary	[0, 0, 0, 1, 0]
multipliers	[0, 0, 0, 1, 0]

Table 6. The first five entries of the fourth hash table

Word	Subject-wise Count
inorganic	[0, 2, 0, 0, 0]
programmer	[0, 0, 2, 0, 0]
unity	[1, 0, 0, 0, 0]
repair	[1, 0, 0, 0, 0]
evolutionary	[2, 0, 0, 0, 0]

Table 7. The first five entries of the fifth hash table

Word	Subject-wise Count
inorganic	[0, 2, 0, 0, 0]
programmer	[0, 0, 2, 0, 0]
unity	[1, 0, 0, 0, 0]
repair	[1, 0, 0, 0, 0]
evolutionary	[2, 0, 0, 0, 0]

Table 8. The first five entries of the sixth hash table

Word	Subject-wise Count
inorganic	[0, 2, 0, 0, 0]
programmer	[0, 0, 2, 0, 0]
unity	[1, 0, 0, 0, 0]
repair	[1, 0, 0, 0, 0]
evolutionary	[2, 0, 0, 0, 0]

The titles in each subject are numbered from 1 to 60. For each test, 10 titles from each subject have been used as the testing set and the remaining 50 titles from each set have been used as the training set. Thus, each test involved a training set of 250 book titles and a testing set of 50 book titles.

Table 9. Test Results using Word Frequency

Test Case	Training Set	Testing Set	Accuracy
1	Nos. 11-60	Nos. 1-10	78%
2	Nos. 1-10, 21-60	Nos. 11-20	86%
3	Nos. 1-20, 31-60	Nos. 21-30	82%
4	Nos. 1-30, 41-60	Nos. 31-40	80%
5	Nos. 1-40, 51-60	Nos. 41-50	76%
6	Nos. 1-50	Nos. 51-60	90%

The results of the initial testing using only the word frequency methodology, used in the previous work in [1], are shown in Table 9. It is clear from Table 9 that less than satisfactory results were obtained with average prediction accuracy of 82% (246 correct class predictions out of 300 total test instances). This was below the 83.6% accuracy as was obtained using the same methodology for the binary classifier in the previous work [1]. A slight dip in accuracy is explainable because of the smaller training dataset (300 instances instead of the 500 that were used in [1]) and the increased number of classes (5 instead of 2) but nevertheless, a higher level of accuracy was desired.

Thus, the inverse class frequency property was incorporated into the classifier, as has been explained in previous sections. This helped to rectify many incorrect predictions that previously happened because of generic words like ‘introduction’, ‘techniques’, ‘methods’, etc. which had a high frequency of occurrence but weren’t intrinsic to any specific subject. Using the wf-icf property, the classifier has been re-tested using the same dataset and the results obtained have been shown in Table 10 below.

Table 10. Test Results using WF-ICF

Test Case	Training Set	Testing Set	Accuracy
1	Nos. 11-60	Nos. 1-10	82%
2	Nos. 1-10, 21-60	Nos. 11-20	92%
3	Nos. 1-20, 31-60	Nos. 21-30	82%
4	Nos. 1-30, 41-60	Nos. 31-40	84%
5	Nos. 1-40, 51-60	Nos. 41-50	88%
6	Nos. 1-50	Nos. 51-60	94%

As is evident, a much higher level of accuracy has been obtained, with an average accuracy of 87% (261 correct predictions out of 300 total data instances). Though accuracy below 90% does not seem exceptionally high, the training dataset only contains 300 instances which is quite small for training a text classifier. It can be expected that using a larger training dataset would allow the classifier to achieve an accuracy of above 90% since more is the number of training instances, higher is the level of accuracy achieved by the classifier.

Table 11 lists all 39 incorrect predictions made by the classifier along with their actual class and the class predicted by the classifier. An important fact revealed by this table is nearly half (17 out of 39) of the incorrect predictions mistakenly identified Biology as the correct class. Most of these are cases in which none of the words in the test instance could be found in the training set (or more specifically, in the hash table constructed from the training set) and thus the classifier did not know how to deal with these words, leading to the instance getting a wf-icf score of 0 for all classes. In the cases when the wf-icf scores of two or more classes are the same, the predicted class will be the one which appears first in the order (Biology, Chemistry, Computer Science, Mathematics, Physics). Thus here, when the wf-icf score is 0 for all classes, the predicted class label would be Biology. Clearly, this issue can be resolved by using a larger number of training instances so that more concepts related to the different classes can be captured in the dataset used to train the classifier.

This table also reveals that incorporating word stemming would be very useful in improving accuracy as presently the classifier treats words like ‘Math’, ‘Mathematics’, ‘Mathematician’, ‘Mathematical’ etc. as completely different from each other and so a book title such as ‘Mathematical Intro to Logic’ cannot be identified by the classifier as a mathematics book even though it knows that a title with the word ‘mathematics’ is a mathematics book. Plural and singular forms of the same word also contribute to reducing classifier accuracy for the same reason.

Table 11. Incorrect Predictions

No.	Book Title	Actual	Predicted
1	Biological Signal Analysis	Biology	Maths
2	Biophysical Techniques	Biology	Chemistry
3	Elements: A Visual Exploration	Chemistry	Biology
4	Alchemy of Air	Chemistry	Biology
5	Uranium	Chemistry	Biology
6	AI: A Modern Approach	CS	Biology
7	Book of Proof	Maths	Chemistry
8	Character of Physical Law	Physics	Chemistry
9	Physicist’s World	Physics	Chemistry
10	Skeptical Chemist	Chemistry	Biology
11	Learn You a Haskell for Great Good	CS	Biology
12	Electromagnetism, Principles, Applications	Physics	Maths
13	Static & Dynamic Electricity	Physics	Biology
14	Physical Methods for Chemists	Chemistry	Physics
15	Applied Cryptography	CS	Maths
16	Database System Concepts	CS	Biology
17	Compilers: Principles, Techniques, Tools	CS	Chemistry
18	Hacker’s Delight	CS	Biology
19	Introduction to Database Systems	CS	Biology
20	Introduction to Statistical Thought	Maths	Physics
21	Strange Theory of Light & Matter	Physics	Chemistry
22	Theory of Universal Wave Function	Physics	CS
23	Molecular Driving Forces	Chemistry	Biology
24	Computational Complexity	CS	Maths
25	Debugging	CS	Biology
26	Communication Networks	CS	Biology
27	Introductory Statistics	Maths	Chemistry
28	Lectures on Statistics	Maths	Physics
29	Math in Society	Maths	Chemistry
30	Math, Numerics, Programming	Maths	CS
31	Immune System	Biology	CS
32	Pro Git	CS	Biology
33	Method of Lagrange Multipliers	Maths	Biology
34	Mathematicians	Maths	Chemistry
35	Gravitation	Physics	Biology
36	First Course in General Relativity	Physics	Chemistry
37	Linux Command Line	CS	Biology
38	Universal History of Computing	CS	Chemistry
39	Mathematical Intro to Logic	Maths	Physics

Regardless of all these issues, a considerably satisfactory level of prediction accuracy has been obtained with the proposed classifier. One disadvantage of incremental classification is that if an instance is incorrectly classified, the classifier’s accuracy is lesser for future classifications. This problem is reduced as larger datasets are used in the training phase.

To determine the runtime complexity of the training and classification processes, let the number of training instances be N (i.e. the size of the dataset used to train the classifier has N instances). Additionally, let the number of words in the largest training instance be M and let the number of different classes (i.e. the number of unique class labels) contained in the training dataset be C.

The initialization phase simply involves looping through the training dataset in order to load the instances into the program along with their corresponding class labels and then running another loop through the labels to determine the number of unique classes. Thus, this phase is bounded by O(N).

In order to train the classifier, the algorithm loops through each of the N training instances and for each such instance, it must loop through each of its constituent words. For each of these words, the index of the corresponding class label of the current training instance is determined and the related word count array is updated accordingly.

Thus the time complexity of the training phase is bounded by O(N×M) since the largest training instance consists of M words. Each such instance must be preprocessed before being used to train the classifier by converting to lower case and then removing stop words and punctuation. To do this pre-processing, the algorithm must loop through each instance and compare each word in the instance with the stop words. Let the number of stop words that the classifier can detect be s. Then, the stop word removal process has complexity O(s×M). However, s is a constant as the number of stop words is fixed for the classifier. Thus, this complexity may be rewritten as s×O(M) which reduces to O(M). Similarly, punctuation removal and lower case conversion require only a loop through each word in each instance, and thus for each individual instance, the pre-processing time complexity is O(M) and hence the overall complexity of the training phase for each instance is bounded by O(M).

The classification phase works similar to the training phase but has an additional level of complexity for each instance. It requires iterating through each word in the instance to be classified and for each word, iterating through the different classes in order to determine the wf-icf values for each class. Thus, the complexity of classifying each instance is O(M×C). Hence, the classifier has a quadratic runtime complexity for the overall training process as well as for classification process for a single instance.

• VI.    Conclusion and Future Scope

In this paper, the proposed work has successfully improved upon the work that as was done in [1] by converting the incremental binary text classifier into an incremental N-class text classifier. Further, the classifier’s prediction accuracy was improved upon by incorporating the wf-icf property (based upon the well known tf-idf property of information retrieval).

As discussed in the previous section, an important and useful extension that can be made to the classifier in the future is incorporating word stemming into the training and classification processes. This would allow the classifier to treat different forms of the same word as the same concept and thereby improve the classification accuracy. Several of the incorrect predictions in Table 5 were caused due to the lack of this feature.