A Fuzzy Preference Relation Based Method for Face Recognition by Gabor Filters

Published Online June 2012 in MECS

• I.    Introduction

  Facial recognition system is one of the most remarkable abilities human being enjoys. It is important for several aspect of our social life. Machine recognition of faces has recently emerged as one of the most important area amongst researchers in Mathematics and Computer science. As one of the most successful application of image analysis has recently got great deal of attention from researchers across the globe which is evident from the growing number of conferences and research that has taken places. Computer analysis of face images deals with visual signals (light reflected of the surface of a face) that is registered by a digital sensor or an array of pixel value.The pixel can encode intensity.Though a formal method of classifying faces was first proposed by Francis Galton in 1888. The use of face recognition is immense, face recognition technology has numerous law enforcement and commercial applications [7][16]. Face recognition can efficiently replace the use of pin numbers and passwords. The passwords and pin numbers are difficult to remember although they are

very helpful for authentication but they can be easily stolen. Applications where face recognition can be used efficiently include secure transactions in e and m commerce. On the other hand Fuzzy preference relation has been time and again used effectively by many authors for decision making the concept of complete fuzzy relation and incomplete fuzzy relations [8] gives two different approaches for decision making based on the information supplied by the decision maker (DM) [9] in our case the machine. This paper has been organized in the following way section 2, deals with existing work ,3 with the proposed work , 4 with implementation and section 5 with results and conclusion.

• II.    Existing work

  There are numerous face recognition techniques that have been proposed in the last few decades [7]. This existing techniques can be broadly divided into few categories [16]. Due to the simplicity and the efficiency for the feature extraction and representation , many subspace analysis methods , such as principal component analysis PCA, linear discriminant analysis LDA, independent component analysis ICA and locality preserving projections LPP , are widely used for face recognition [1][2]. In 1960, digital image processing was proposed with semi automated systems. In order to locate the major features different marks were made on the photographs. These system uses features like mouth, eyes, and nose. Next to get the common reference points the ratios and distances were calculated and then compared with the database [7]. In 1970’s Harmon , Goldstein and Lesk introduced their system [2]. The system had 21 subjective makers having tip thickness and hair color. This was difficult while automating the system because many complex measurements were made by hand. Fisher and Elschlagerb projected a new advancement to face recognition. Another approach is connectionist technique which is used to categorize human faces using two things which are gestures and a set of classifying markers. This technique is normally applied on neural network principles and 2-dimensional pattern recognition. In normal networks a huge training database of faces is needed which required too much

time to train the whole system to get the desired results. [7] Shariff , Khalid, Raza, Mohosin proposed a mechanized technique for general pattern recognition.

• III.    Proposed work

In the proposed system , we use Gabor filters for face recognition [7] . Gabor wavelets are widely and successfully used in face recognition due to their biological relevance and computational properties. The Gabor wavelets can be defined as follows [16],

^'L^;/-(3

iW^^e(1)

Where и and v denote the orientation and scale of Gabor kernels, z=(x,y), H-H denotes the norm operator, and the wave vector k^^ is defined as follows,

,v^v

Where k„ = ^ , (pu=m

Is the maximum frequency and / is the spacing factor between kernels in the frequency domain. The gabor kernels are all self similar since they can be generated from one filter , the mother wavelet by scaling and rotation via the wave vector k_M , _v . Each kernel is a product of a Gaussian envelope and a complex plane wave , while the first term in the square bracket determines the oscillating part of the kernel and the second term compensates for the DC value. In each filtered image we find the maximum intensity points dynamically and are then marked as fiducial points ( Landmarks on faces) [7]. The main objective in the proposed work is to match the face with the faces in the database [5]. For this we use the concept of complete Fuzzy preference relation. The leftmost corner point of each faces which are stored in the data base are marked as the origin and respect to this point the distances of every other fiducial point is calculated by the distance formula. This distance data of each points for every face are then stored in the database. Next in the face which is to be matched , the same coordinate system is used and the distances of each fiducial points are calculated. Now the distance of each fiducial point is compared with the already stored data and a complete fuzzy preference relation matrix is obtained. The largest eigen value of this matrix is obtained and the corresponding eigen vector is determined from which the decision is being made [8]. The step wise rules for the method which we are proposing in this paper can be schematically given by the flowchart as follows.

Flow chart for the proposed method.

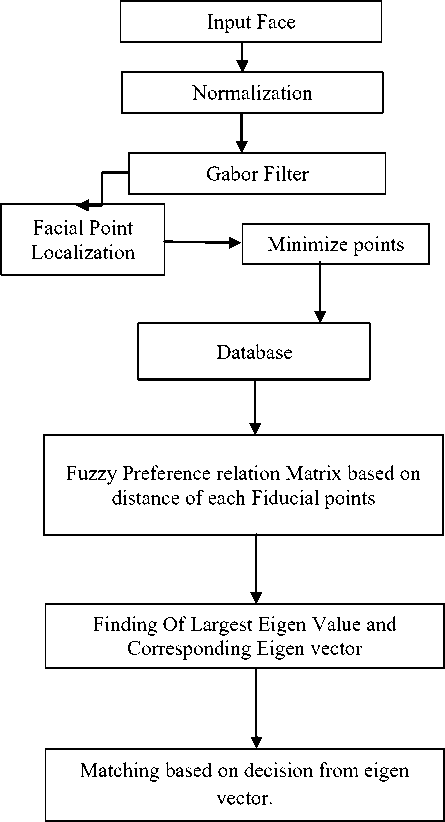
• 3.1    Complete fuzzy preference relation

3.2 Some properties of complete fuzzy preference relation

In the process of decision making [8], a DM generally needs to compare a set of decision alternatives with respect to a criterion and construct a preference relation. Complete fuzzy preference relation is a common preference relation which can be described as follows [9].

Let X = {x1, x2, x3,...........xn} be a finite set of alternatives. A complete fuzzy preference relation "P" on X is a fuzzy set on the product set "X X X" that is characterized by a membership function pp:X XX ^ [0,1]. The DM (Machine in our case) preferences on X are given by a complete fuzzy preference relation P = (Pij)nxn, where рц £ [0,1] рц + pn = 1 , pu = 0-5 V i,j and py denotes the preference degree or the intensity of the alternative over . In particular, py = 0 indicates that Xj is absolutely preferred to X; ; рц < 0-5 indicates that Xj is preferred to Х[ . Pij>0.5 indicates thatXt is preferred to Xj .

Pij =0.5 indicates indifference between X[ and ^Xj .

fuzzy preference relation , then such a preference relation is given by

1.Tanino (1984) introduced the concept of multiplicative transitivity

Pij =            ∀ i , j .

W_t +        , .

In this case p can be expressed as follows

™ ⁼ where ph >0 ∀^1, I ^.

=

w1+w1

™H w_n+w₁

w1+w2

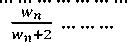
w1+wn

™H w_n+w_n.

PikPkjPji ⁼           ∀ i ^, j ^, к .

Pa + Pjk ≥ Ptk ∀ i , j , к

Pij ≥ 0.5, Pjk ≥0.5⇒ Ptk ≥0.5 ∀ i , j , к

Ptk ≥ min { Pij , Pjk } ∀ i , j , к .

Ptk ≥ max { PH , Pjk } ∀ i , j , к .

Pij ≥0.5 , Pjk ≥0.5⇒ Ptk ≥ min { Pij , Pjk } ∀ i , j , к .

Pij ≥0.5 , Pjk ≥0.5⟹ Ptk ≥ max { PH , Pjk } ∀ i , j , к .

Saaty (1980) introduced the well known eigen vector method to determine the priority vector “ w ” of the general multiplicative preference relation :

Xw =        where ^•max is the largest eigen value of A.

Similarly let w =(w^ , w₂,……… ….. ) T be the priority vector of the fuzzy preference relation = ( Pij )n× „ where Wi >0, I = 1,2, ….. . ∑ "=lWi =1. If p =( Pij )_n×n is a multiplicative consistent complete

From equation 2. It follows that the following system of equation can be given wi

( w_t + Wi)+        ( Wi + W₂ )

Wi + w_±           Wi + w₂

+ ⋯…………………

W_t + W_n )= TIWi

+ i=1,2,…………n.               (3)

Using the general complete fuzzy preference relation P=(Pij )    instead of the multiplicative consistent complete fuzzy preference relation in equation 4, and using ^■max instead of П it follows that ( Lipovetsky and Michael Conklin 2002)

Pit ( Wi + Wi)+ Pi2 ( Wi + w₂ )+⋯….. + Pin ( Wi +

W_n)= ^•max^i ^∀ i                              (4)

Where Wt >0 , i =1,2,… ….. . ∑ 'i=i^wi =1

By solving equation (3) together with ∑ 'Uwi =1 we can get the value of ^■max and the priority vector w=( w^ , w₂ ,……Wn )T corresponding to ^-max .

• IV.    Implementation

• 4.1    Normalisation

• 2.Pixels adjustment:

• 3.Boundaries are smoothed.

• 4.4 Fiducial point localization

The whole methodology proposed above is implemented on a input face as shown below.

Fig 1: The Input Face

The following are the steps for image normalization which is applied over all the stored images in the database as well as the input face which is to be recogonised. The following are the steps of normalization.

1.Rescaling to 128× 128

In this step, image pixel intensities are used, such that the standard deviation of image pixel is one and mean zero.

After applying the gabor filter 40 images are required with different angles and orientations. Then the maximum intensity points are found in each image. After that 40 points on image are calculated [7][16] . To find this face points following equations is used

^{∑  ∑}   . max ( Хц )/ where X = , j

I =                                    , j .

• 4.2 Gabor filter

In this step gabor filter is applied on the input face [7]. The sample 40 gabor filters are shown below in fig (1) [7] . This figures are obtained using five dissimilar scales and eight angles are engaged and in result of it 40 gabor filters are acquired fig (2)[7].

Fig 4: The circles in the face showing intensity points

Fig 2: Gabor Filter

The maximum intensity points are shown in the figure (4) above.

^i and ^2 are the width and height of image. By using this equation one point is found on each image out of 40 gabor filtered images. Then the distance is calculated to minimize the points. The minimum distance possible between two points is defined to maximize the number of points.

The reduced number of points are shown below in the figure (5).

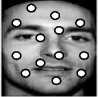
Fig 5: The reduced number of points are marked

4.5 Distance matrix for fiducial point in terms of complete fuzzy preference relation

To obtain the distance matrix for fiducial point in terms of complete fuzzy preference relation we take six fiducial points for the person whose face is being detected and we also keep the data of six fiducial points for six different persons in the database of the system. We use the matrix given in [8].

Faces in Database

0.5

0.3  0.6

Where the input image I ( X ,у) and the resultant image J ( X ,у) of gabor filter. When the original image with gabor filter is multiplied. A new image is acquired which is equal to J ( X ,у), where x and у is the height and width of the image respectively. From [7],

A= Input Face

0.7

0.4

0.7

⎣0.7

0.5  0.7

0.3  0.5

0.4  0.6

0.2  0.3

0.3  0.80.3

0.6  0.60.8

0.4  0.50.7⎥

0.5  0.40.8⎥

0.2  0.30.5⎦

By using equation (3) above and ∑ t=lWi = 1, we can establish the following system of equations.

h , j ( x ,У)= I ( x ,У)× 9ц ( X ,У)               (5)

3.28 W₁ +0.3 w₂ + 0.58w₃ +0.3w₄+0.8w₅+0.3w₆ ⁼

0.7Wi + 4.38w2 +0.7w3 +0.6w4+0.6w5 +0.8w6 =

0.42Wi+0.3w2 + 3.34w3 +0.4w4+0.5w5+0.7w6 =

0.7w4+0.4w2 +0.6w3 + 3.899w4+0.4w5+0.8w6 =

0.2w4+0.4w2 +0.5w3 +0.6w4 + 3.405w5+0.7w6 =

0.7w4+0.2w2 +0.3w3 +0.2w4+0.3w5 + 2.699w6 =

This system of equations can be transformed into the following eigenvalue problem

Bw ⁼

Together with ∑ t=lWi =1 , where,

	⎡3.9	0.3	0.6	0.3	0.8	0.3⎤
	0.7	4.9	0.7	0.6	0.6	0.8⎥
	0.4	0.3	3.3	0.4	0.5	0.7⎥
В =	0.7	0.4	0.6	3.9	0.4	0.8⎥
	0.2	0.4	0.5	0.6	3.4	0.7⎥
	0.7	0.2	0.3	0.2	0.3	2.7⎥
	⎣

By solving this eigenvalue problem we get the value of ^max and the priority vector “w” corresponding to ^-max as follows,

^max = 6.00

and w = (0.137,0.289,0.136,0.201,0.151,0.086) T

Ranking of the alternatives based on priority vector "w” can be done as follows, w6 < w3 < WT < w5 < w4 < w2

and thus the most preferable alternative is W2 .

Therefore from the above drawn conclusion we can say the input face resembles the face of person stored as M2 in the database of the system.

To find the largest eigen value and the corresponding priority vector we will apply the numerical method if the order of the matrix becomes large for which we suggest a algorithm which we have used for C programming to obtain the largest eigen value.

Step2. Read n and the given matrix ( ^aij ) for = 1(1) n J = 1(1) n ;

Step3: For i = 1(1)n, set ^xi =1

Step4: For к = 1(1)20

Step5: For i = 1(1) n

Step6: Set Xi =0

Step7: For j = 1(1) n

Step8: set Xi =  ⁺ Cl[jXj

Step9: Next j , Next i

Step10: m =

Step11: For i = 2(1) n

Step12: If m < Xi , set m =

Step13: Next I

Step14: For i = 1(1) n set Xi ₌

Step15: Write the numerically largest eigen value.

Step16. Stop.

• V. Experiments and results

• 4.6 Algorithm to determine the largest eigen value

To measure he effectiveness and accuracy of the proposed method the standard database 94 [15][7] is used. For this twenty person’s images were selected. There were twenty images of each person in the database.

Comparison of Result:-

	Total Images	Matched	Unmatche d	Result in %
Peoposed Techniques	2	2	0	100
	10	10	0	100
	14	13	1	92.85
	20	18	2	90.00
	25	23	2	92.00
	30	28	2	93.3
	35	32	3	91.4
Existing Techniques	Eigenface [12]			80.00
	Elastic graph matching [13]			80.00
	EBGM [14]			75.29

Step1. Start the program

In the proposed method total 136 images were compared of which 10 were not matched. So overall percentage of success in this method is 92.64%.

• VI. Concluding Remarks

The proposed technique of face recognition gives a new approach based on complete fuzzy preference relation. The use of complete fuzzy preference relation in decision making while recognizing the faces is better than many other method. The reason being the fact that a human face has the possibility of transformation it may become fat or thin depending upon the physical changes of human body, in this extreme cases also this method is expected to give better results, The efficiency of the method can be further enhanced by increasing the number of fiducial points. However the efficiency of the method largely depends on the accuracy in construction of the fuzzy preference matrix. This technique also opens up a new approach in face recognition techniques for future research.