A Fuzzy Programming Technique for Solving Multi-objective Structural Problem
Автор: Samir Deya, Tapan Kumar Roy
Журнал: International Journal of Engineering and Manufacturing(IJEM) @ijem
Статья в выпуске: 5 vol.4, 2014 года.
Бесплатный доступ
This paper proposes a new fuzzy multi-objective optimization approach to solve a multi-objective nonlinear programming problem in context of a structural design. We have been developed a multi-objective structural problem of a planar truss structural model in fuzzy environment. Here, the objectives are (i) to minimize weight of the structure and (ii) to minimize the vertical deflection at loading point. In this model, the design variables are the cross-section of the truss members and the constraints are the stresses in members. This approach is used to solve the structural model under uncertainty based on different operator. A numerical illustration is given to support our approach.
Structural Optimization, Fuzzy Optimization, Generalized fuzzy number
Короткий адрес: https://sciup.org/15014373
IDR: 15014373
Текст научной статьи A Fuzzy Programming Technique for Solving Multi-objective Structural Problem
Optimization involves maximizing or minimizing an objective function (e.g. cost, weight) of a Structural system which has been frequently employed as the evaluation criterion in Structural engineering applications. In real life Structural optimization problems, usually more than one objective are required to be optimized, such as minimum mass or cost , maximum stiffness, minimum displacement at specific structural points and maximum structural strain energy. This makes it necessary to formulate a multi-objective optimization model. Scientist Pareto introduced the concept of Pareto solution of multi-objective optimization problem. Since then the determination of the compromise set of a multi-objective problem is called Pareto optimization which finds application in engineering and other fields. Pareto optimization has been in use ever since. Different optimization algorithms and techniques are used to solve structural optimization problem, like Ray
* Corresponding author. 03412252108; fax: 03412254248
optimization[14], artificial bee colony algorithm[17], particle swarm optimization[10,13,16], genetic algorithm[11,15], ant colony optimization[12,13] etc.
Practically, the problem of structural design exhibits nonlinearity, and is aptly represented as a non-linear programming problem with both objective functions and constraints functions. Coefficients or parameters of non-linear Structural models are assumed to be deterministic and fixed. But, there are many situations where they may not be exactly known i.e. they may be somewhat uncertain in nature. Thus decision making methods under uncertainty are needed. The fuzzy programming has been proposed from this point of view. In decision making process, fuzzy set theory was first implemented by Zadeh [2]. Then Zimmermann [4] proposed a fuzzy multi-criteria decision making set, defined as the intersection of all fuzzy goals and their constraints. Several researchers like Wang et al. [1], Rao [7], Yeh et.al [6], Xu [5], Shih et.al [8,9] made distinctive implementation of the fuzzy set theory to optimize Structural model.
In the real world, we have to deal with imprecision on a regular basis. A fuzzy number is a quantity whose value is imprecise, rather than exact as is the case with ordinary numbers. Fuzzy numbers offer a realistic depiction of the outside world. It may well serve as the validation representation of the imprecise data. Fuzzy decision making is implemented here. The decision makers should assess the alternatives with fuzzy number and rank them accordingly before making a decision. The ranking of fuzzy numbers is of utmost importance while solving a fuzzy programming problem. The ranking outcomes vary with every decision-maker as they differ in their preference and perspective. Bortolan and Degani [18] have made a proposition with regard to the ranking of fuzzy number. Here, the ranking method of Liou and Wang [20] has been considered for the sake of simplicity.
In this paper we have introduced fuzzy multi-objective mathematical programming with generalized Trapezoidal fuzzy number and it is applied as objective and constraints coefficients to a structural problem subject to stress constraints. Pareto optimal solution of this multi-objective mathematical programming is established. The structural model consists of two objectives. They are (i) to minimum weight and (ii) to minimum vertical deflection of loaded joint. Numerical example has been provided to illustrate the problem.
The remainder of this paper is organized in the following way. In section 2, we discuss about Multiobjective Structural Model of a three bar truss. In section 3, we discuss about prerequisite mathematics i.e. fuzzy set, convex fuzzy set, normal fuzzy set and generalized fuzzy number. In section 4, we discuss about fuzzy structural model with imprecise applied load and imprecise material density. In section 5, we discuss about mathematical analysis like fuzzy programming technique to solve MONLP using max-min operator and max-additive operator. Solution of crisp multi-objective structural model by fuzzy programming technique and numerical solution of structural model of three bar truss are discussed in section 6 and 7 respectively. Finally we draw conclusions from the results in section 8.
-
2. Multi-objective Structural Optimization Model of a Three-Bar Truss
A well-known three bar [9] planar truss structure is considered. The design objective is to minimize weight of the structural WT ( A , A 2) and minimize the vertical deflection 5 ( A i , A 2 ) at loading point of a statistically loaded three-bar planar truss subjected to stress ст, ( A , A ) constraints on each of the truss members i = 1,2,3 .
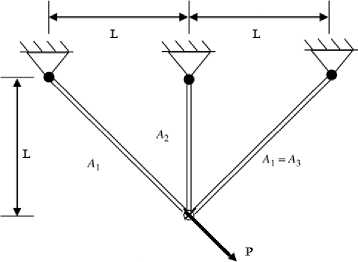
Fig. 1. Design of the three-bar planar truss
The multi-objective structural optimization problem (MOSOP) can be stated as follows:
Minimize WT ( A 1 , A 2 ) = p L ( 2 72 A 1 + A 2 ) ,
PL minimize 5 ( A 1 , A 2 ) = —------——-,
E ( A 1 + 2AA 2 )
P (72 A 1 + A 2 ) subject to " ( A i ,A 2 ) ■ R 2 < [ " t ] ,
2 A|a 2 + 2 A A|
P
" 2 ( A"A 2 ) ■ A +ж " ] ’
" з ( 4’ A 2 ) ■ 111PA 2 Я Я <[ " ] ’
2 AA + V2 A
A min < A < A max , i = 1,2.
Where P = applied load; p =material density, L = Length, Allowable tensile stress = [ " T ] .Allowable compressive stress = [ " c ] , Young’s modulus = E , A 1 = cross section of bar-1 and bar-3 A 2 =cross section of bar-2.
-
3. Prerequisite mathematics
Fuzzy set theory was first introduced by Zadeh [2] in 1965 as a mathematical way of representing impreciseness or vagueness in everyday life.
-
3.1. Fuzzy set
-
3.2. Convex fuzzy set
-
3.3. Normal fuzzy set
-
3.4. Generalized Fuzzy Number (GFN)
A fuzzy set A in a universe of discourse X is defined as the following set of pairs A = { ( x , ^ ( x ) ) : x e X } .Here ^ : X ^ [0,1] is a mapping called the membership function of the fuzzy set
A and ц ( x ) is called the membership value or degree of membership of x e X in the fuzzy set A .The larger ^A ( x ) is the stronger the grade of membership form in A .
A fuzzy set a of the universe of discourse X is convex if and only if for all x 1, x 2 in x ,
^ ( Я x 1 + ( 1 - Я x 2) > min ( ^ ( X j ) , ^ ( x 2) ) ) when0 < Я < 1.
A fuzzy set A of the universe of discourse X is called a normal fuzzy set implying that there exist at least one x e X such that ^ ( x ) = 1 .
In [21,22], Chen represented a generalized trapezoidal fuzzy number (GTrFN) A as A = ( a , b , c , d ; w ) where 0 < w < 1 and a , b , c and d are real numbers. The generalized fuzzy number A is a fuzzy subset of real line R , whose membership function ^ ( x ) satisfies the following conditions:
-
( 1 ) ^A ( x ) is a continuous mapping from R to the closed interval [0,1].
-
( 2 ) ^ ( x ) = 0 where -да < x < a ;
-
( 3 ) ^A ( x ) is strictly increasing with constant rate on [ a , b ]
-
( 4 ) ^ A ( x ) = w where b < x < c ;
-
( 5 ) ц ( x ) is strictly decreasing with constant rate on [ c , d ];
-
( 6 ) ^ ( x ) = 0 where d < x < да .
Note: A is a convex fuzzy set. It will be normalized for w = 1.
If w = 1, the generalized fuzzy number A is called a trapezoidal fuzzy number (TrFN) denoted
A = ( a , b , c , d ) .
-
( i ) If a = b and c = d , then A is called crisp interval [ a , b ] .
-
( ii ) If b = c , then A is called a generalized triangular fuzzy number (GTFN) as A = ( a , b , c ; w )
-
( iii ) If b = c , w = 1 then it is called a triangular fuzzy number (TFN) as A = ( a , b , c ) .
-
( iv ) If a = b = c = d and w = 1, then A is called a real number a .
-
3.5. Definition
A GTrFN A = ( a , b , c , d ; w ) is a fuzzy set of the real line R whose membership function ^ : R ^ [0, w ] is defined as
|
^l ( * ) = w ^ b - a J |
for a < x < b |
|
^ w ( * ) = w ( \ 1 d - x ^. ( x ) = w [ d - c j |
for b < c < c for c < x < d |
|
0 |
otherwise |
where a < b < c < d and w e (0,1]
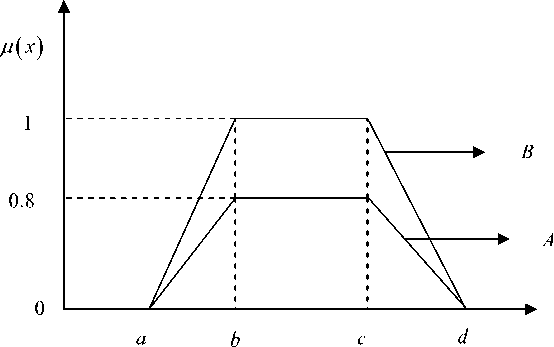
Fig. 2. Two generalized trapezoidal fuzzy number A and B
Figure 2 shows two different GTrFNs A = ( a , b , c , d ; W 1 ) and B = ( a , b , c , d ; W 2 ) which denote two different decision maker’s opinions. The values w 1 and w 2 represents the degrees of confidence of opinions of decision makers A and B respectively .Here w 1 = 0.8 and w 2 = 1.0.
Because of the traditional fuzzy arithmetic operations we can deal with any normalized fuzzy numbers, they not only change the type of membership function of fuzzy number after arithmetical operations, but also have a drawback of requiring troublesome and tedious arithmetical operations. Thus Chen [21] proposed the function principle, which could be used as the fuzzy numbers arithmetic operations between generalized fuzzy numbers, where these fuzzy arithmetic operations can deal with the generalized fuzzy numbers. In Hsieh and Chen [19] pointed out that arithmetic operators on fuzzy numbers presented in Chen [21] does not only change the type of membership function of fuzzy numbers after arithmetic operations, but they can also reduce the trouble sameness and tediousness of arithmetical operations. Thus in this paper, we use Chen’s [21]
fuzzy numbers arithmetical operators to deal with the fuzzy number arithmetical operations between generalized fuzzy numbers.
The difference between the arithmetic operations on generalized fuzzy numbers and the traditional fuzzy numbers is that the former can deal with both non-normalized and normalized fuzzy numbers, but the latter can only deal with normalized fuzzy numbers. Let X e [0,1] be a pre-assigned parameter called the degree of optimism. The graded mean [22] value (or, total X -integral value) of A is defined as
IX (A) = XIR (A) + (1 — X) IL (A) where IR (A) and IL (A) are the right and left interval values of A defined as
I L ( A Ml ( ^A ) 1 “ d “ J/ w
IR (A )=UW (AA Г ada J Л
Now, for GTrFN A = ( a , b , c , d ; w )
( ^-A )- 1
а = a + a ( b - a ) and ( ц "д ) a = d - a ( d - c )
Therefore the left and right integral values are ILw
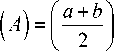
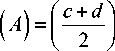
Hence the total X -integral value of A is I X R
and IRw
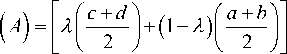
The total X -integral value is a convex combination of the right and left integral values through the degree of optimism. The left integral value is used to reflect the pessimistic viewpoint and the right integral value is used to reflect the optimistic viewpoint of the decision-maker. A large value of X specifies the higher degree of optimism. For instance, when X = 1 , the total integral value
I W ( A ) = [ c + d ] = I R ( A )
represents an
optimistic viewpoint. On the other hand, when X = 0, the total X -integral value is I R
(A =[ a + b ]
I 2 J
= IR (A)
represents a pessimistic viewpoint. When X = 0.5 the total X -integral is I RS
a + b + c + d
. It reflects
a moderately optimistic decision-makers viewpoint and is the same as the defuzzification of the fuzzy number A .
-
4. Fuzzy Structural Model
In our multi-objective structural optimization problem (MOSOP), we have considered that the applied load
P and material density p as fuzzy number, the above crisp model (1) reduces to
Minimze WT (A1, A2 ) = pL (242A1 + A2), minimize 5 (A1, A2) =
PL
E ( A 1 + 2 AA 2 )
subject to с 1 ( A, A 2 ) ^
P (72 A1 + A 2 ) 2 A A + 2AA 2
<[ c T ] ,
P
' 2 ( A 1’ A 2 ) " А ГЖ C ] ’
"3 1 A1, A 2 ) " тртрр^ 'C ] ’
2 A j A 2 + 2 A A ^
A, min < A < A, max , i = 1,2.
The generalized trapezoidal fuzzy numbers here represent the applied load and material density. This are
P = ( P , P , P , P ; W j ) and p = ( p , p , p , p ; w2 ) . For a fixed value of X , the X -integral value for P and p
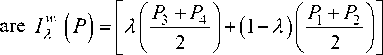
and Iw 2
X
(p = X p 'p- ] + ( i - X ) | P L± p A v’ I 2 3 7( 2
.Using the X -
integral values of the fuzzy applied load P and fuzzy material density p in the above problem (2) we get
Minimize WT ( A 1, A 2 ) = Ip ( p ) L ( 2V2 A 1 + A 2 ) ,
I w1 ( P ) L minimize 5 ( A 1 , A 2) = — -----——-,
E ( A 1 + 2AA 2 )
I X 1 ( P ) (72 A j + A 2 ) subject to cr, ( A , A ) ^------------ < [ c
1V 1 2^ 2 AA + 72 A 2 L
c 2
( A i ’ A 2 )
I X 1 ( P )
A 1 + 72 a 2
<[ c T ] ,
Iw1 P A c (A, A)- X ( )X 2 <[c], 3V 1 27 2AA + 72A2
A min < A < A max ,i = 1,2.
-
5. Mathematical Analysis
-
5.1 Fuzzy programming technique to solve MONLP problem
-
A multi-objective non-linear programming (MONLP) or a vector minimization problem (VMP) may be taken in the following form:
Minimize f ( x ) = [ f ( x ) , f 2 ( x ) ,...., fk ( x ) ] T
subject to x e X = {x e Rn : gj (x) < or = or >bj for j = 1,2,..., m; x > 0}, and li < xi < ui, i = 1,2,...,n
Zimmermann (4) showed that fuzzy programming technique can be used to solve the multi-objective programming problem.
To solve MONLP problem, following steps are used
Step 1: Solve the MONLP (4) as a single objective non-linear programming problem using only one objective at a time and ignoring the others, these solutions are known as ideal solution.
Step 2: From the result of step 1, determine the corresponding values for every objective at each solution derived. With the values of all objectives at each ideal solution, pay-off matrix can be formulated as follows
|
f 1( x ) |
f 2 ( x ) … |
. fk ( x ) |
|
|
x 1 |
f 1 *( x 1) |
f 2 *( x 1) … |
. f k *( x 1) |
|
x 2 |
f 1 *( x 2) |
f 2 *( x 2) … |
. f k *( x 2) |
|
xk |
f 1 *( xk ) |
f 2 *( xk ) |
f k *( xk ) |
Here x 1 x 2 , x 3 ,….., xk are the ideal solutions of the objectives f 1( x ), f 2( x ),….., fk ( x ) respectively.
So Ur = max { fr ( x 1), fr ( x 2),......, fr ( xk ) } and Lr = min { fr ( x 1), fr ( x 2),......, fr ( xk ) } for r = 1,2,...., k
Where Ur and Lr be upper and lower bounds of the rth objective function f r ( x ) for r = 1,2,3,........, k .
Step 3: Using aspiration level of each objective of the MONLP (4) may be written as follows:
Find x so as to satisfy fr (x)< Lr for r = 1,2,3,........, k
x e X.
Here objective functions are considered as fuzzy constraints. These types of fuzzy constraints can be quantified by eliciting a corresponding membership function
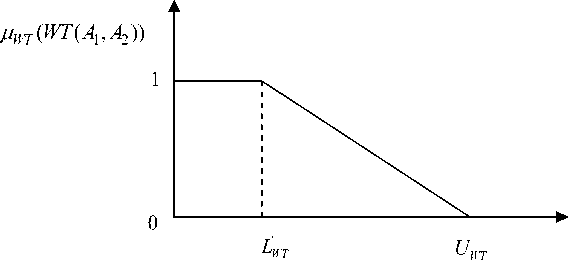
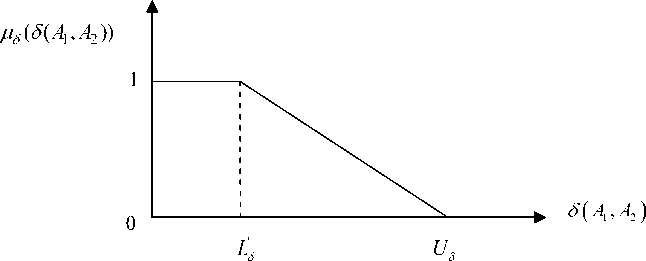
0 if ( x ) ^ U r
M w ( f r ( x )) ^ w r
U r - f r ( X ) U r — L r
If L r < f r ( X ) < U r ,
wr ff fr (X) < Lr r = 1,2,3,..., k
Here ^ w r ( f r ( x ) ) is strictly monotonic decreasing function with respect to fr ( x ) and Lr = Lr + e. where
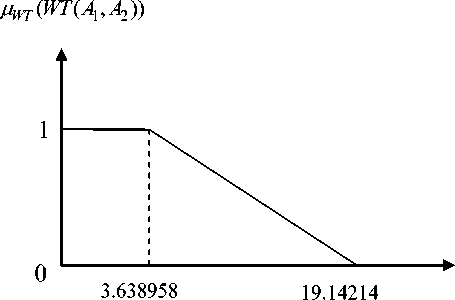
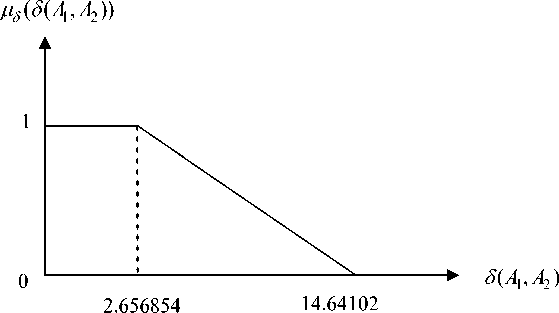
0 Fig. 3. Rough sketch of membership for objective functions f. (x) Having elicited the membership functions (as in (5)) pw (fr (x)) for r = 1,2,3,........,k, introduce a general r aggregation function, Mw (x) = F (mW (f1( x)), ^; (f,(x)),......, ^- (fk (x))) D12 k So a fuzzy multi-objective decision making problem can be defined as Maximize Mw (x) D subject to x e X. According to fuzzy decision [3] based on max–min operator , the problem (7) is reduced to Maximize а WrMw (/r (x))> а subject to x е X а е [0,1] Where Wr > 0 for all r = 1,2, Zk r=, Wr=1. According to fuzzy decision [3] based on max-additive operator, the problem (7) is reduced to k Maximize Mw (x; W) = ^ WrMw (/r (x)) r=1 r subject to x е X 0< Mrwr (/r (x))< Wr, for r = 1,2,....,k Zk r=, Wr=1. Where Wr > 0 for all r = 1,2, Step 4: Solve (8) and (9) to get Pareto optimal solutions. To solve MOSOP (1) step-1 of (5.1) is used. From the result of step 1, determine the corresponding values for every objective at each solution derived. With the values of all objectives at each ideal solution, pay-off matrix can be formulated as follows: WT (A1, A2) £( A!, A2) A11, A21 WT *( A1, A2) A( A1, a2) A12, A22 WT (A2, A22) f( A2, A22) From the pay-off matrix, the bounds U^ = max {WT (A1, A1), WT (A2, A )} and L^ = min{WT(A1, A1), WT(A2, A)} for weight function WT(A,A) (where LiV1< WT(Ax,A) < U^) and the bounds U5 = max {A( A1, A1), ^( A2, A22)} and Ls = min *A( A1, A1), ^( A2, A2)} for deflection function ^( A1, A2 ) (where Ls< ^(Ax, A ) < Us) are identified. Here for simplicity linear membership functions Mt (WT(A,A)) and M ( ^(A,A)) for the objective functions WT(A,A) and S(A1, A2) respectively are defined as follows: w1 »W (WT(4, A2)) = ^ w1 Uwt - WT(Ai, A2) UWT - Lwtt ifWT(Ai, A2) < L^ ifL^^ WT(Ai, A2) < Uwt if WT(Ai, A2) > Uwt WT ( Ax, A2) Fig. 4. Rough sketch of membership for objective weight function WT ( A, A ) 4w2(5(Д, A)) = . w2 W2 • U5 - 5(4, A2) U5 - L if 8(A1, A2) < L if L< 5(4, A2) < U5 5 7 if 5(A1, A2) > U5 Fig. 5. Rough sketch of membership for objective weight function 5 ( A, A2 ) where Lwt = Li+ei,Ls = L2 +e2,ei e(0,Uwt — Lwt),e2 e(0,Us — Ls) According to step-3, having elicited the above membership functions crisp non-linear programming problem is formulated as follows: Using max-min operator Maximize a subject to W w Uwr - WT (A1, A2 ) Uwr-LWT >a, W2 w2 U5 - 8( A1, A ) U - L 8 8 > a, "1 ( AL A2 )- P (72A1 + A2) 2 A1 A2+ 72A °t ], °2 (A1, A2 ) - °3 (A1, A2 ) - P A1 + 72A2 PA2 <[°T ], 2 AA + 72A2 I ° ], Am”< Ai< Amax,i = 1,2., W1 + W2 = 1. The problem (10) can be written as Maximize a subject to W1 fj Uwt - WT (A1, A2) W . ( UWT - LWT > a W2 w ' U8 - 8(A1, A2))) U - L 11 V 8 8 )) > a P 72 A + A °1 ( A1, A2 )-J, .F4)<[°T ], 2 AA2 + 2A A P °2 (A1, A2)-A+2AA-° ]. "3(A1-A2)-PA2^2-<°]• 2 A1A2 + 2 A A1 Amin < Ai< Aimax,i = 1,2. W = min(W1, w2),W1 + W2= 1. where W and W are two normalized positive weights of two objectives. Using max-additive operator Maximize W w. ' UWT - WT(A1, A2))) U -Z I - V WT WT /) + W2w2 ' U8 - 5(A1, A)W U - L 11 V 5 $ ) ) ) subject to 0 < w. Uwt - WT (A^ A2) UWT-LWT < w, 0 < w2 ' U5 - 5(A1, A2)' U - L V 5 5 ) < w2, "1(A1,A2) - P (72A + A2) <["T L P "2(A1’A2)-AW2A " ]’ "3 (Ai’A2 )- ,PA2 FF ^]’ 2 AA + 2 A A Ai™1" < A< Amax,i = 1,2., Wi+ W2= 1. The problem (12) can be written as Maximize w U5 - 5( A1, A2) ]l + W WI I 2 U - LII V V 5 5))) subject to 0 < Wj " UWT - WT (A1, A2)' V UWT-LWT ) < Wj; 0 < w2 ' U5 - 5(A1, A2)) V U5 -L5 ) < w2 p V2 A + A " (A, A)- -----=4 <[" ], 1V 1 27 2 A1A2 + 72 A2 L TJ P "2(A1'A2)-A+MA, "l"r]’ " (A’ A,)----PAF^T<["]’ 3V 1 27 2AA^ + 72A2 L LJ A™in< A< Amax’i = 1’2. w = min(w,’ w2)’W, + W2 = 1. where W and W are two normalized positive weights of two objectives. The input data for MOSOP (1) is given as follows Table 1. Input data for crisp model (1) Applied load P (KN) Material density p (KN / m3) Length L (m) Maximum allowable tensile stress <ТГ (KN / m2) Maximum allowable compressive stress ^c (KN / m2) Young’s modulus E (KN / m2) Aminand max A of cross section of bars (10-4m2) Amm = 0.1 2 x107 Amax = 5 20 100 1 20 15 Amin = 0.1 Amax = 5 Solution: According to step 2 pay off matrix is formulated as follows: WT(A1,A2) S( A1, A2) A1 2.638958 14.64102 A2 19.14214 1.656854 Here U = 19.14214 , L = 2.638958 , U2= 14.64102 , L = 1.656854 , L = 3.638958 , ^= 1 , L = 2.656854 , e2 = 1 .Here linear membership function for the objective functions WT(AvA2) and 3(A1, A2) is defined as follows: [0.6 AWT (WT (A1, A2)) = <0.6 19.14214 - WT (A, A) 15.503182 if WT(A!, A2) < 3.638958 if 3.638958 < WT(A!, A2) < 19.14214 if WT(A!, A2) > 19.14214 WT (A1, A) Fig. 6. Rough sketch of membership for objective weight function WT ( A, A ) [0.8 if 5(A1, A2) < 2.656854 ц5(5(4, A2)) = <0.8 14.64102 - 5( A, A) 13.984166 if 2.656854 < 5(A1, A2) < 14.64102 if 5(A1, A2) > 14.64102 Fig. 7.Rough sketch of membership for objective deflection functions 5 ( A, A ) Considering the Pareto optimal solutions of the MOSOP (1) with different weights by GFNLP method based on different operator is given in table 2 and table 3 respectively. Table 2. Pareto optimal solutions of MOSOP based on max-min operator with different weights W1 W2 A x10-4 m2 A x10—4 m2 wt ( a , a )x102kn 5 (A, A )x10“6 m 0.5 0.5 0.5927786 3.362761 5.039392 3.739408 0.6 0.4 1.267122 5.000000 8.583962 2.398602 0.4 0.6 0.597794 1.738530 3.429341 6.543551 Table 3. Pareto optimal solutions of MOSOP based on max-additive operator with different weights W1 W2 A x10-4 m2 A x10—4 m2 wt ( a , A )x102kn 5 (A, A )x10"6 m 0.5 0.5 0.5995887 3.789761 5.485654 3.356200 0.6 0.4 0.5858620 3.003582 4.4660650 4.137730 0.4 0.6 0.6111046 4.752674 6.481139 2.727620 Fuzzy model: Considering the GTrFN for applied load and material density of the FMOSOP (2) we take applied load 20 KN = (17,19,21,23;0.8) KN and material density 100 KN/m3= (97,99,100,103;0.9) KN/m3and other input data are same as in crisp model (Table 1). The Pareto optimal solutions of the fuzzy multi-objective structural model (FMOSM) with different weights by GFNLP method based on different operator are given when X = 0.5 in table 4 and table 5 respectively. Table 4. Pareto optimal solutions of FMOSOP based on max-min operator with different weights for X = 0.5 W1 W2 A x10-4 m2 A x10-4 m2 wt ( a , A )x102kn 5 (A, A )x10"6 m 0.5 0.5 0.5927786 3.362761 5.026793 3.739408 0.6 0.4 1.267122 5.000000 8.562502 2.398602 0.4 0.6 0.5977921 1.738530 3.420768 6.543551 Table 5. Pareto optimal solutions of FMOSOP based on max-additive operator with different weights for X = 0.5 W1 W2 A x10-4 m2 A x10-4 m2 wt ( a , a )x102kn 5 (A, A )x10"6 m 0.5 0.5 0.5995887 3.789761 5.471939 3.356200 0.6 0.4 0.5858620 3.003582 4.648999 4.137730 0.4 0.6 0.6111046 4.752674 6.464936 2.727620 The Pareto optimal solutions of FMOSOP for different values of X based on different operator are presented in table 6 and table 7 respectively. Decision Maker (DM) can get the optimal solutions according to desire. Table 6. Pareto optimal solutions of FMOSOP based on max-min operator with equal weights Test A x^-4m2 A x10-4m2 wt ( a , A )xi02kn 5 (A, A )x10-6m Optimistic i.e X = 1 0.6480025 3.479624 5.392138 3.950487 About optimistic i.e X = 0.7 0.6149335 3.410561 5.173030 3.824798 Moderate i.e X = 0.5 0.5927786 3.362761 5.026793 3.739408 About pessimistic i.e X = 0.2 0.5593784 3.288189 4.807035 3.608736 Pessimistic i.e X = 0 0.5369965 3.236407 4.660157 3.519772 Table 7. Pareto optimal solutions of FMOSOP based on max-additive operator with equal weights Test A x10-4m2 A x10-4 m2 wt ( a , A )xi02kn 5 (A, A )x10-6m Optimistic i.e X = 1 0.6562311 3.949402 5.892586 3.524778 About optimistic i.e X = 0.7 0.622975 3.854818 5.640209 3.424526 Moderate i.e X = 0.5 0.5995887 3.789761 5.471939 3.356200 About pessimistic i.e X = 0.2 0.5653916 3.688927 5.219351 3.251289 Pessimistic i.e X = 0 0.5425019 3.619376 5.050727 3.179609 Table 8. Optimal solutions MOSOP based on different operators with equal weights Operator A x10-4 m2 A x10-4 m2 wt ( a , A )xi02kn 5 (A, A )x10"6m max-min 0.5927786 3.362761 5.039392 3.739408 max-additive 0.5995887 3.789761 5.485654 3.356200 From the above empirical investigation, it is cleared that max-min operator gives better structural weight where as max-additive operator gives better node deflection. A comparative study for fuzzy multi-objective structural optimization based on different operator has been discussed here. Numerical solution shows that the FNLP technique is effective in achieving minimum structural weight and minimum node deflection by max-min operator and max-additive operator respectively. Here decision-maker may obtain the optimal results according to his expectations of optimistic/pessimistic/ moderate values of weights and node deflection. This method presented is quite simple and can be applied to other areas of engineering science. The authors declare that there is no conflict of interests. The authors are grateful for the valuable comments and suggestions from the respected reviewers which have enhanced the strength and significance of our work. [1] Wang,G.Y.,Wang, W.Q., “ Fuzzy optimum design of structure.” Engineering Optimization 1985; 8: 291300. [2] L. A. Zadeh, Fuzzy set, Information and Control 1965; 8(3): 338-353. [3] R.E. Bellman and L.A. Zadeh, “Decision-making in a fuzzy environment,” Management Science 1970; 17(4): B141-B164. [4] Zimmermann, H.J., “fuzzy linear programming with several objective function” Fuzzy sets and systems 1978; 1: 45-55. [5] Xu, C. “Fuzzy optimization of structures by the two-phase method”, Computer and Structure 1989; 31(4): 575–580. [6] Yeh, Y.C, and Hsu, D.S. “Structural optimization with fuzzy parameters”. Computer and Structure 1990; 37(6): 917–924. [7] Rao, S.S., “Description and optimum Design of Fuzzy Mathematical Systems”, Journal of Mechanisms, Transmissions, and Automation in Design 1987; 109: 126-132. [8] Shih,C. J. and Lee, H. W. “Level-cut Approaches of First and Second Kind for Unique Solution Design in Fuzzy Engineering Optimization Problems”, Tamkang Journal of Science and Engineering 2004; 7( 3): 189-198. [9] Shih, C.J., Chi, C.C. and Hsiao, J.H. “Alternative α -level-cuts methods for optimum structural design with fuzzy resources”, Computers and Structures 2003; 81:2579–2587. [10] Perez, R.E. and Behdinan, K.: Particle swarm approach for structural design optimization, Computers & Structures 2007; 85 (19-20):1579-1588. [11] Kaveh, A., Rahami, H., “Nonlinear Analysis and Optimal Design of Structures via Force Method and Genetic Algorithm,” Computers and Structures 2006; 84:770-778. [12] Kaveh, A, Talatahari S. “An improved ant colony optimization for the design of planar steel frames.” Eng Struct 2010; 32(3):864–873. [13] Kaveh, A., Talatahari, S., “Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures”. Computers and Structures 2009; 87(56):267–283. [14] Kaveh, A., Khayatazad, M., “Ray optimization for size and shape optimization of truss structures”. Computers and Structures 2013; 117:82–94. [15] Dede T, Bekirog .lu S, Ayvaz Y. “Weight minimization of trusses with genetic algorithm”. Appl Soft Comput 2011; 11(2):2565–2575. [16] Luh GC, Lin CY. “Optimal design of truss-structures using particle swarm optimization.” Computers and Structures 2011; 89(2324):2221–2232. [17] Sonmez M. “Discrete optimum design of truss structures using artificial bee colony algorithm”. Struct Multidiscip Optimiz 2011; 43(1):85–97. [18] G. Bortolan, R. Degani, A review of some methods for ranking fuzzy numbers, Fuzzy Sets and systems 1985;15: 1–19. [19] C.H. Hsieh, S.H. Chen, “Similarity of generalized fuzzy numbers with graded mean integration representation,” in: Proc. 8th Int. fuzzy Syst. Association World Congress, Taipei,Taiwan, Republic of China, 1999 ;2: 551–555. [20] T.S. Liou, M.J.J. Wang, “Ranking fuzzy numbers with integral value,” Fuzzy Sets and Systems 1992; 50: 247–255. [21] S.H. Chen, “Operations on fuzzy numbers with function principal,” Tamkang Journal of Management Science 1985; 6 (1): 13–25. [22] S.H. Chen, “Ranking generalized fuzzy number with graded mean integration,” Proceedings of 8th International Fuzzy System Association World Congress, Taipei, Taiwan, Republic of China 1999;2:899–902. Authors Profile Samir Dey is an Assistant Professor in the Department of Mathematics of Asansol Engineering College, Asansol, West Bengal, India He received M.Sc (Applied Mathematics) degree from Institute of Engineering Science and Technology, Shibpur, West Bengal and a M.Tech (Operations Research) degree from National Institute of Technology, Durgapur, India. His research interest is in Fuzzy Mathematics. He is currently working toward the Ph.D. degree. Tapan Kumar Roy is a professor in the Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, West Bengal, India. He has published lots of papers on Fuzzy and Intuitionistic Fuzzy set Theory, Inventory, Transportation, Reliability Optimization, Portfolio Optimization, Fuzzy and Stochastic Optimization, etc.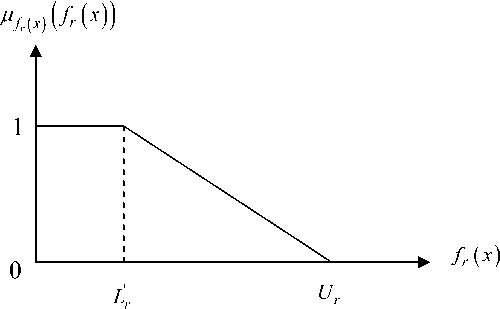
6. Fuzzy Programming Technique to Solve Crisp Multi-Objective Structural Model
7. Numerical Solution of a Multi-objective Structural Optimization Problem (MOSOP) of a Three-Bar Truss:
8. Conclusions


Список литературы A Fuzzy Programming Technique for Solving Multi-objective Structural Problem
- Wang,G.Y.,Wang, W.Q., " Fuzzy optimum design of structure." Engineering Optimization 1985; 8: 291-300.
- L. A. Zadeh, Fuzzy set, Information and Control 1965; 8(3): 338-353.
- R.E. Bellman and L.A. Zadeh, "Decision-making in a fuzzy environment," Management Science 1970; 17(4): B141-B164.
- Zimmermann, H.J., "fuzzy linear programming with several objective function" Fuzzy sets and systems 1978; 1: 45-55.
- Xu, C. "Fuzzy optimization of structures by the two-phase method", Computer and Structure 1989; 31(4): 575–580.
- Yeh, Y.C, and Hsu, D.S. "Structural optimization with fuzzy parameters". Computer and Structure 1990; 37(6): 917–924.
- Rao, S.S., "Description and optimum Design of Fuzzy Mathematical Systems", Journal of Mechanisms, Transmissions, and Automation in Design 1987; 109: 126-132.
- Shih,C. J. and Lee, H. W. "Level-cut Approaches of First and Second Kind for Unique Solution Design in Fuzzy Engineering Optimization Problems", Tamkang Journal of Science and Engineering 2004; 7( 3): 189-198.
- Shih, C.J., Chi, C.C. and Hsiao, J.H. "Alternative -level-cuts methods for optimum structural design with fuzzy resources", Computers and Structures 2003; 81:2579–2587.
- Perez, R.E. and Behdinan, K.: Particle swarm approach for structural design optimization, Computers & Structures 2007; 85 (19-20):1579-1588.
- Kaveh, A., Rahami, H., "Nonlinear Analysis and Optimal Design of Structures via Force Method and Genetic Algorithm," Computers and Structures 2006; 84:770-778.
- Kaveh, A, Talatahari S. "An improved ant colony optimization for the design of planar steel frames." Eng Struct 2010; 32(3):864–873.
- Kaveh, A., Talatahari, S., "Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures". Computers and Structures 2009; 87(56):267–283.
- Kaveh, A., Khayatazad, M., "Ray optimization for size and shape optimization of truss structures". Computers and Structures 2013; 117:82–94.
- Dede T, Bekirog .lu S, Ayvaz Y. "Weight minimization of trusses with genetic algorithm". Appl Soft Comput 2011; 11(2):2565–2575.
- Luh GC, Lin CY. "Optimal design of truss-structures using particle swarm optimization." Computers and Structures 2011; 89(2324):2221–2232.
- Sonmez M. "Discrete optimum design of truss structures using artificial bee colony algorithm". Struct Multidiscip Optimiz 2011; 43(1):85–97.
- G. Bortolan, R. Degani, A review of some methods for ranking fuzzy numbers, Fuzzy Sets and systems 1985;15: 1–19.
- C.H. Hsieh, S.H. Chen, "Similarity of generalized fuzzy numbers with graded mean integration representation," in: Proc. 8th Int. fuzzy Syst. Association World Congress, Taipei,Taiwan, Republic of China, 1999 ;2: 551–555.
- T.S. Liou, M.J.J. Wang, "Ranking fuzzy numbers with integral value," Fuzzy Sets and Systems 1992; 50: 247–255.
- S.H. Chen, "Operations on fuzzy numbers with function principal," Tamkang Journal of Management Science 1985; 6 (1): 13–25.
- S.H. Chen, "Ranking generalized fuzzy number with graded mean integration," Proceedings of 8th International Fuzzy System Association World Congress, Taipei, Taiwan, Republic of China 1999;2:899–902.


