A genetic algorithm based fractional fuzzy PID controller for integer and fractional order systems

Published Online May 2018 in MECS

Fractional calculus has been used for long, but was reintroduced in a mathematically rigorous form by Leibnitz [1] [2]. Fractional calculus has been used quite effectively for physical systems modeling as evidenced by some seminal research papers, e.g., mechanical system design using fractional calculus [3], fluid flow modeling using a fractional form of conservation of mass [4], control of resonant plants or the CRONE [5], and in biomimetic controller formulation [6].

A fractional formulation of physical systems brings the approach closer to an actual system or represents the system more precisely [7]. Furthermore, fractional calculus does reduce computational complexity of the controller design process. Standard practice is to implement a fractional system by approximating it to its integer order counterpart, while preserving attributes of the original system [8]. In literature on fractional calculus, we generally find techniques that give transfer functions of pretty high orders. Hence more appropriate approach is to go for methods that reduce these higher order systems to, at the most, first or second order systems.

Fuzzy logic has been used in several fields to tackle complex problems and essentially mimics human way of thinking and analyzing [9]. Fuzzy logic has been used in several practical applications, e.g., automatic operation and control of trains [10][11][12][13][14]. We can design a fuzzy controller either as a standalone one or in conjunction with conventional control to improve performance of a hitherto poor controller. It has also been used quite effectively in tackling nonlinearities and noise. Most widely used paradigms wherein fuzzy systems come handy are fuzzy supervisory control and fuzzy adaptive control [15]. Fuzzy systems employ an approximate reasoning based inferencing mechanism to capture expert knowledge and feature extraction. Fuzzy systems are found to produce better strategies than conventional control.

Genetic algorithm (GA) belongs to what may be termed as evolutionary algorithms and was first proposed in the seventies. GA is based on the evolution of chromosomes and is linked to research on human genome, in specific, how they modify themselves in passing from one generation to the next. GA is thus a nature inspired technique [16]. Several researchers have used GA in diverse fields, e. g., control systems design and optimization [17] [18]; designing of VLSI chips [19]; control and maneuvering of space vehicles [20]; robot control [21]; image processing [22]  [23]; multiple processors scheduling [24]; designing of signal processing systems [25].

In fractional order based PID control, GA has been combined with particle swarm optimization (PSO) for efficient control [26][27][28][29]. Applications include aero fin control using this hybrid approach to minimize rise time, peak overshoot and peak time of the response [30]. Fractional order PID control has also been used to control an unmanned aerial vehicle with good disturbance handling; PSO imparting robustness to the designed controller [31]. Another application of Fractional Order PID (FOPID) is the speed control of DC motors [32] [33], wherein artificial bee colony algorithm with GA has been used for optimization. A neuro fuzzy FOPID control technique has been implemented in [34]. Finally, linear quadratic regulator based FOPID has been proposed in [35] which minimize integral time absolute error and integral of square error.

FOPID control has also been used for wind power optimization using permanent magnet synchronous motor [36] [37]. In [36] PSO has been used to optimize the parameters of FOPID and then fuzzy logic is employed for further tuning of the controller. Integer order system control by posing it as a fractional order system has been proposed in [38], wherein parameter X acts as input to the fuzzy controller, and µ as output. A review of physical-fractional and biological-genetic operators for modeling and control of industrial process by using multi objective genetic algorithm to optimize the parameters of the FOPID is analyzed in [39]. In [40], authors have presented fractional-order feedback controller for control and synchronization of fractional-order chaotic systems.

This work aims at hybridizing the GA into a fuzzy fractional PID controller for optimizing the performance of FOPID control. GA is first used to find the most optimal FOPID parameters and then the resulting controller is hybridized with a fuzzy logic based fractional PID controller. This results in a fuzzy fractional controller with superior performance than a pure FOPID control. GA is used to search for the best fit or the most optimal parameters based on given performance index and fuzzy logic based controller is used to optimize the PID parameters. We compare the performance of our controller against a contemporary fractional PID controller [38].

Rest of the paper is organized as: section II gives theoretical background on fractional order control, fuzzy control technique, integer approximation of the fractional order plants or the approximate transfer function; section III gives details of the proposed hybrid fuzzy fractional PID controller. Section IV gives simulation results and comparative evaluation with other fractional order controllers on several integer order and fractional systems for two cases: (i) with disturbances and (ii) without disturbances. Section V is the concluding section.

• II.    Fuzzy Fractional PID Controller.

• A.    Fractional Order Control

Fig. 1 gives the block diagram of a fractional PID controller represented by PI X D^. The controller transfer function can be described in s-domain and t-domains as:

T fopid ( s ) = Us) = K p + K i S" ^л + V ; ( Л Ц >  0)  (1)

E ( s )

u ( t ) = K_pe ( t ) + KD - ^ e ( t ) + K_DD*e ( t )      (2)

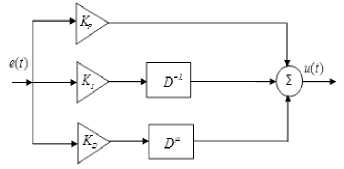
Fig.1. Fractional PID control

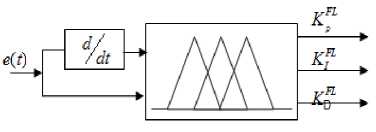
Fig.2. PID like Fuzzy Controller wherein TFOPID(s), U(s), E(s) represent controller transfer function, error and output signals, respectively. KP, KI, KD , λ and µ are FOPID parameters.

• B.    Fuzzy Logic based Control

Controllers based on fuzzy logic (FL) try to form a control policy by emulating human reasoning and analyses. Fuzzy logic based control is easy to comprehend and implement as it involves very limited mathematics (in majority of the cases). Typical implementation of a PID like fuzzy logic controller (Fig. 2) involves tuning of PID parameters for minimizing the error ( e ) and change in error (Δ e ) [35] which act as inputs to the controller. Selection of error ( e ) and change in error (Δ e ) as inputs is an efficient and simple way to design the FL controller. There are various types of membership functions that can be laid over these input variables with consequent inference mechanisms; we have chosen Gaussian membership functions and a Mamdani Inference for ease of implementation. The membership functions for the consequents have been taken as Gaussian as in [41].

We fuzzify both the inputs by laying Gaussian membership function over their universe of discourse. The term set for each linguistic variable has 3 subsets; leading to a total of 9 rules for each of the three PID parameters. Thus total number of rules for all the three PID parameters is 27 (9 for each) and is used for implementing the fuzzy logic PID (FLPID) controller. We calculate the membership values for each of the variable as:

^ lp ⁽ x j ) = exp

^{- (} x j - x j ^{) 2}

2 ^

)

; l p = 1,2,3; j = 1,2

wherein fuzzy labels for the three fuzzy subsets are designated by lp , corresponding to variable j (3). For the Gaussian membership functions centers and width are:

x j = a j + b j ( l_p - 1) with a 1 = - 0.7, a ₂ = - 0.02; b 1 = 0.45 b = 0.02 and widths: g , 0.09, g ₂=0.004.

• C.    Genetic Algorithm based Fractional PID (GAFOPID) Control

In the proposed approach, we use genetic algorithm as a first step for coarse tuning of the fractional order parameters; these coarse tuned parameters are than fine tuned using fuzzy logic. We choose integral time absolute error (ITAE) as the fitness function for the GA based optimization. We employ FMINSEARCH algorithm for unconstrained optimization of the hybrid function.

• D.    Approximating Fractional Order Systems

Typical controller implementation for fractional order systems involves integer order approximation of the underlying fractional order system. There exits several approximation methods in literature; we use the Oustaloup approximator [42] for reducing the order of the fractional order system. If the order is still high, we employ the sub-optimum H2-norm [43] for further order reduction of the fractional system. This is a standard technique for analysis and control of fractional order systems; reduced order system has reduced complexity with lower order (1, 2 or max 3) and possesses all the attributes of original fractional system. Oustaloup filter is given as:

G oust

M s + w

( s ) = K П ----;

j = 1 s + w .

J J

where zeros, poles and gain are defined as:

2j-1-n                   2j-1+n wj. = wiwhM  ; wj. = wfwhM  ; K = wn tou = (юfh / юfl)1/2, П being fractional order of differ integrator, M being order of the filter, [ωfl ωfh] represents desired frequency range of interest; which must be set before beginning the design process.

• III.    GA Based Hybrid Fuzzy Fractional PID Control

In the proposed approach, we seek to reap the benefits of the GA and fuzzy logic based tuning of controllers by hybridizing GA and fuzzy fractional design approaches. More specifically, we use conventional fuzzy approach for designing the PID like fuzzy controller along with a GA assisted mechanism for tuning the fractional plant parameters.

We use GA as the initial tuning algorithm with optimization parameters: population size is 20, selection function is stochastic, cross over fraction is taken as 0.8, cross over function is chosen as scattered and mutation function is taken as constrained dependent. This initial optimization phase provides us with coarse tuned parameters for the FOPID controller. Next, fuzzy logic based mechanism is used which takes error and change in error as inputs and generates K ^FL , K ^FL and K ^FL values (tuned). As a result, we get 27 rules for the FLPID controller, which are listed in Table 1.

Table 1. Rules for the FLPID Controller

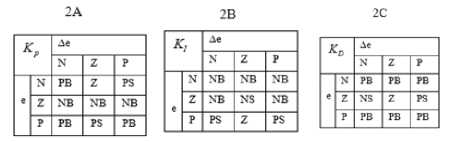
In the above table, N, Z and P stand for linguistic labels corresponding to “Negative”, “Zero” and “Positive”, respectively.

We hybridize the values obtained via the GA and fuzzy logic based techniques for the K P , K I and K D parameters:

GA     FL

K p = K p + K p

= k^'a + k F FL

GA     FL

K D = K D ⁺ K D

The resulting hybrid fractional fuzzy PID (HFFPID) controller is depicted in Fig. 3.

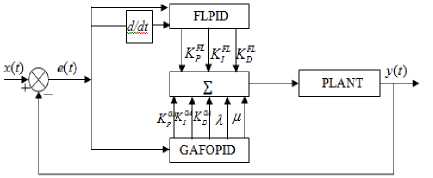
Fig.3. HFFPID controller block diagram

A close look at the Fig. 3 reveals that parameters for the HFFPID have been obtained through a cooperation of GA and fuzzy logic based solutions. FLPID controller optimizes the fuzzy PID parameters and a mix with the fractional parameters generates the HFFPID controller. The transfer function for the HFFPID controller is:

G hffpid ( s ) = K p + K i S - " + K o s " (6)

GA optimizer gives the direction for minimizing the performance index while fuzzy logic rule base provides the inference mechanism needed for controller realization. A combination of GA and fuzzy logic based tuning of parameters generates an adaptive optimal controller.

• IV.    Simulation Results

We simulate our proposed GA based hybrid fuzzy fractional control on several integer and fractional order benchmark problems.

• A.    DC motor control

Our first case study is DC motor control, which is a second order system with transfer function:

G DC _ M ^{( s} )  0.005 s ₂ + 0.06 s + 0.1001

To find a restricted search space for GA assisted FOPID controller, we employ Ziegler Nichol (ZN) tuning. The ZN provides us with coarse search space for further tuning of the PID parameter values and is listed in Table 2. The use of ZN for finding the initial estimates of the PID parameter values leads to quick search results later on with the help of GA and fuzzy logic.

Table 2. PID Parameter Values (ZN)

K P	K I	K D
136.4	1287	3.62

GA is then used for further optimization of these values in this search space (these values serve as limiting values). The parameters for GA have already been specified in section 2 and ITAE is chosen as the fitness function. The ZN criteria ordained search space for GA is

K p = [0; 136.4], K i = [0; 1287], K d = [0; 3.62], X = [0; 1], µ= [0; 1]

We run GA for about 62 generations (up to the point where incremental fitness value change tends to zero). Optimal parameters obtained at the end of GA run are detailed in Table 3.

Table 3. GAFOPID Controller Parameters

K P	K I	K D	X	µ
94.43	135.23	3.612	0.034	0.988

Tuning performance of the GAFOPID controller is depicted in Fig. 4. We turn off tuning process when the incremental change in the fitness value for two consecutive iterations becomes negligible.

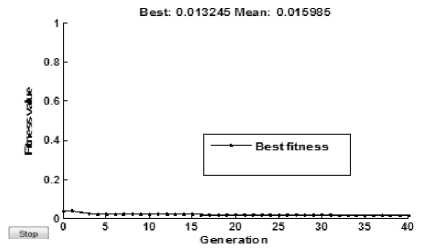
Fig.4. Fitness tuning curve for GAFOPID controller

A.1. Fuzzy Controller

Fuzzy inference based on the rule base (Fig. 2) is then used for refining PID parameters. Optimum FLPID parameters thus obtained are shown in Table 4.

Table 4. FLPID Parameters

K P	K I	K D	X	µ
94.43	135.7	7.587	0.034	0.988

Next step is to hybridize the parameters obtained via GA with the ones obtained with FLPID using (4). We get the transfer function of our HFFPID (PI ^X D^H) controller as:

G hffpid _ DC _ M ( s ) = 94.46 + '35.7 + 7.587 s °"⁸⁸ (8)

Next, we use the Oustaloup approximation [42] for converting this transfer function (8) to a transfer function with integer order as:

^GHFFPID„c _ m ^{( S} )

8.832 s ¹⁶ + 7516 s ¹⁵ + 2.317 e 006 s ¹⁴ + 3.078 e 008 s ¹³ + 1.668 e 010 s ¹²

+ 4.334 e 011 s ¹¹ + 5.661 e 012 s ¹⁰ + 3.478 e 013 s ⁹ + 7.987 e 013 s ⁸ +

• 8.064 e 013 s ⁷ + 3.528 e 013 s ⁶ + 5.303 e 012 s ⁵ + 3.416 e 011 s ⁴ +

3.424 e 011 s ⁷ + 1.484 e 011 s ⁶ + 2.195 e 010 s ⁵ + 1.389 e 009 s ⁴ + 3.737 e 007 s ³ + 3.299 e 005 s ² + 1173 s + 1.472

_         9.367 e 009 s ³ + 8.431 e 007 s ² + 3.058 e 005 s + 391.8

=         1.265 s ¹⁵ + 1028 s ¹⁴ + 2.951 e 005 s ¹³ + 3.411 e 007 s¹²

+ 1.294 e 009 s ¹¹ + 2.087 e 010 s ¹⁰ + 1.44 e 011 s ⁹ + 3.39 e 011 s ⁸ +

This transfer function (9) has a very high order and is therefore reduced to second order with the sub-optimum H2-normapproximation method [43].

We use (10) for DC motor speed control.

A.2. Simulation results on DC Motor

For a unit step input to the DC motor, we compare performance of our HFFPID controller with integer order PID and FOPID controllers. From Fig. 5, we observe that HFFPID controller reaches desired speed quiet smoothly without overshoot with a minimal settling time.

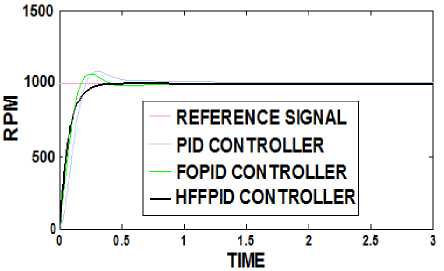
Fig.5. DC Motor control using HFFID for unit step speed

We compare time response parameters of our HFFPID controller against other controllers (Table 5). It may be noted that HFFPID exhibits superior performance. Controller comparison has been made for a square wave target for the DC motor. Fig. 6 shows that HFFPID has superior performance. For judging the robustness of the proposed approach, we test its ability to handle random external disturbances.

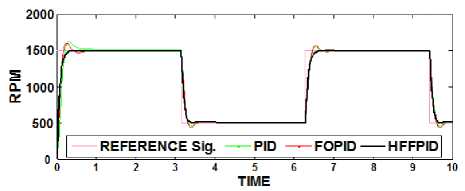
Fig.6. DC motor HFFPID control with square wave target

Table 5. HFFPID response parameters vs. other Controllers

Parameters	Peak Overshoot (%)	Rise time (s)	Settling time (s)	Steady state error
PID	8.32	0.14	0.53	0
FOPID	6.63	0.12	0.35	0.0005
HFFPID	0.07	0.15	0.28	0.0005

(Here) We introduce a sudden disturbance torque of ±300 rpm at t = 2 sec and another one ± 400 rpm at t = 4 sec, corrupting the desired sped input. The tracking performance comparison of different controllers for the step input is shown in Fig. 7. We observe that our HFFPID controller outperforms other controllers in presence of disturbances.

Table 6 gives time response parameters for different controllers for the DC motor speed control (with disturbances). The values depicted in Table 6 bring out the fact that our controller achieves a much superior performance in the disturbed scenario.

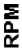
о

f REFERENCE SIGNAL

—PID CONTROLLER FOPID CONTROLLER

—HFFPID CONTROLLER

-200

12  3  4

TIME

• Fig.7. Controller comparison: DC Motor with disturbances

Finally, Fig. 8 gives a comparative evaluation of the controllers for the square wave input with disturbances. We observe that HFFPID controller generates best performance in terms of overshoot and settling time.

• B.    Fractional plant (FOP1)

Our next case study is a fractional plant with transfer function:

G FOP 1 ^{( S} )    ^2.3

+ 3.2 s ¹⁴ + 2.4 s ⁰⁹ + 1

We approximate this transfer function to an integer order transfer function (5th order) by the Oustaloup recursive filter [5] in the frequency range [10-3 103] Hz [44]. Thereafter, it is further reduced to second order as per (121-13).

0.07894 s + 0.2249

^{FOP 1 ( s} ) - s 2 + 0.9852 s + 0.226

• B.1.    Design of HFFPID controller for FOP1

972.9 s + 7.79

Controller design for the system represented by (11) is almost infeasible. Furthermore, the system transfer function generated by using Oustaloup approach (121) is of the order O (35) which is considerably high for representing FOP1.

Bearing these in mind, we proceed to design the HFFPID controller for the reduced order system (13). We follow similar steps (as with the DC motor) for designing the controller , and obtain HFFPID transfer function as:

G hffpid _ fop i ( s ) - 21.62 + 12^ + 42.23 s ⁰²²⁸⁸ (14)

We again make an integer order approximation of (14); represented by (152) and is further reduced to the second order system (16).

HFF™) _ FOP       s ² + 17.44 s + 0.1768     ^{1 J}

5 ³³ + 3173 5 ³² + 4.073 e 6 5 ³¹ + 2.757 e 9 5 ³⁰ + 1.086 e 12 5 ²⁹ + 2.616 e 14 5 ²⁸ + 3.966 e 16 5 ²⁷ + 3.843 e 18 5 ²⁶ + 2.406 e 20 5 ²⁵ + 9.797 e 21 5 ²⁴ + 2.603 e 23 5 ²³ + 4.529 e 24 5 ²² + 5.168 e 25 5 ²¹ + 3.87 e 26 5 ²⁰ + 1.904 e 27 5 ¹⁹ + 6.159 e 27 5 ¹⁸ + 1.309 e 28 5 ¹⁷    (   )

+ 1.83 e 28 5 ¹⁶ + 1.682 e 28 5 ¹⁵ + 1.016 e 28 5 ¹⁴ + 4.036 e 27 5 ¹³ + 1.053 e 27 5 ¹² + 1.803 e 26 5 ¹¹ + 2.025 e 25 5 ¹⁰ + 1.489 e 24 5 ⁹

G FOP _1_ approx ( s )

+ 7.145 e 022 5 ⁸ + 2.23 e 21 5 ⁷ + 4.496 e 19 5 ⁶ + 5.794 e 17 5 ⁵ + 4.698 e 15 5 ⁴ + 2.331 e 13 5 ³ + 6.727 e 10 5 ² + 1.024 e 8 5 + 6.31 e 4 7.943 5 ³⁵ + 2.301 e 4 5 ³⁴ + 2.663 e 7 5 ³³ + 1.614 e 10 5 ³² + 5.684 e 12 5 ³¹ + 1.225 e 15 5 ³⁰ + 1.666 e 17 5 ²⁹ + 1.456 e 019 5²⁸

+ 8.297 e 20 5 ²⁷ + 3.112 e 22 5 ²⁶ + 7.763 e 23 5 ²⁵ + 1.299 e 025 5 ²⁴ + 1.474 e 26 5 ²³ + 1.143 e 27 5 ²² + 6.11 e 27 5 ²¹ + 2.265 e 28 5 ²⁰ + 5.841 e 28 5 ¹⁹ + 1.048 e 29 5 ¹⁸ + 1.31 e 29 5 ¹⁷ + 1.142 e 29 5 ¹⁶ + 6.947 e 28 5 ¹⁵ + 2.96 e 28 5 ¹⁴ + 8.841 e 27 5 ¹³ + 1.845 e 27 5 ¹² + 2.671 e 26 5 ¹¹ + 2.656 e 25 5 ¹⁰ + 1.791 e 24 5 ⁹ + 8.099 e 22 5 ⁸ + 2.426 e 21 5 ⁷ + 4.759 e 19 5 ⁶ + 6.02 e 17 5 ⁵ + 4.82 e 15 5 ⁴ + 2.371 e 13 5 ³ + 6.804 e 10 5 ² + 1.031 e 8 5 + 6.34 e 4

2                            + 9.806 e 22 5 ²⁴ + 1.833 e 24 5 ²³ + 2.248 e 25 5 ²² + 1.812 e 26 5 ²¹ + 9.607 e 26 5 ²⁰ + 3.354 e 27 5 ¹⁹ + 7.715 e 27 5 ¹⁸ + 1.169 e 28 5 ¹⁷   (15)

+ 1.167 e 28 5 ¹⁶ + 7.687 e 27 5 ¹⁵ + 3.334 e 27 5 ¹⁴ + 9.527 e 26 5 ¹³ + 1.793 e 26 5 ¹² + 2.221 e 25 5 ¹¹ + 1.808 e 24 5 ¹⁰ + 9.659 e 22 5 ⁹ + 3.375 e 21 5 ⁸ + 7.689 e 19 5 ⁷ + 1.134 e 18 5 ⁶ + 1.072 e 16 5 ⁵ + 6.392 e 13 5 ⁴ + 2.338 e115 ³ + 4.989 e 8 5 ² + 5.639 e 5 5 + 259.7 HFFPID _ FOP i^{( 5} ) = 1.102 5 33 + 2601 5 32 + 2.498 e 6 5 ³¹ + 1.269 e 9 5 ³⁰ + 3.753 e115 ²⁹ + 6.797 e 13 5 ²⁸ + 7.751 e 15 5 ²⁷ + 5.65 e 17 5 ²⁶ + 2.662 e 19 5²⁵

+ 8.156 e 20 5 ²⁴ + 1.631 e 22 5 ²³ + 2.136 e 23 5 ²² + 1.834 e 24 5 ²¹ + 1.034 e 25 5 ²⁰ + 3.828 e 25 5 ¹⁹ + 9.321 e 25 5 ¹⁸ + 1.491 e 26 5 ¹⁷ + 1.569 e 26 5 ¹⁶ + 1.086 e 26 5 ¹⁵ + 4.936 e 25 5 ¹⁴ + 1.475 e 25 5 ¹³ + 2.898 e 24 5 ¹² + 3.735 e 23 5 ¹¹ + 3.158 e 22 5 ¹⁰ + 1.748 e 21 5 ⁹ + 6.315 e 19 5 ⁸ + 1.484 e 18 5 ⁷ + 2.254 e 16 5 ⁶ + 2.188 e 14 5 ⁵ + 1.337 e 12 5 ⁴ + 5.006 e 9 5 ³ + 1.091 e 7 5 ² + 1.257 e 4 5 + 5.894?

Table 6. Response specifications of controllers

Parameters	Peak Overshoot (%)	Rise time (s)	Settling time (s)	Steady state error
PID	16.07	0.09	0.93	0
FOPID	25.49	0.06	0.35	~ 0
HFFPID	13.76	0.05	0.48	~ 0

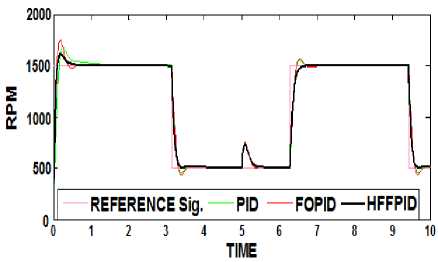
Fig.8. DC motor with disturbances: HFFPID Control

• B.2.    Simulation results on FOP1

We simulate both HFFPID and FOPID controllers on fractional plant 1 for a step input. The results (Fig. 9) show that our approach has better relative stability than FOPID controller. This is corroborated by the response parameter comparison of the controllers (Table 7). It is pretty evident that our HFFPID control has superior peak overshoot, settling time and rise time or an overall superior performance.

Table 7. Time Response Comparison of Controllers: FOP1

Parameters	Peak Overshoot (%)	Rise time (s)	Settling time (s)	Steady state error
FOPID	9.303	0.352	1.597	0
HFFPID	4.535	0.254	1.034	0

We also compare response of controllers when subjected to a square wave input (Fig. 10). Fig. 11 shows controller comparison when random disturbances affect the controller. Disturbances equivalent to 10% of the input amplitude Gaussian distributed are introduced. In Fig. 12, we give comparative performance of controllers with square wave input and disturbances. From these figures it is easy to see that our HFFPID controller has an edge over the FOPID controller and can handle disturbances effectively.