A Heterogeneous Access Remote Integrating Surveillance Heuristic Model for a Moving Train in Tunnel
Автор: Tanuja.P.Patgar, Shankaraiah
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 3 vol.8, 2016 года.
Бесплатный доступ
Many number of real time applications are available for train monitoring using satellite based navigation system with high level of speed and precision. But these systems have faced lot of issues such as multipath loss and line of sight which results in lesser accuracy measurements. When the train is moving in low satellite visible areas such as tunnels, mountains, forest etc, then no position information is available. The service failure in tunnel made big challenge to demonstrate a self supporting innovative platform for navigation of train. This paper is focused on designing a novel approach by integrating Wireless Sensor Network (WSN) and Radio Frequency Identification (RFID) system for continuous monitoring of train moving in tunnel. The wireless tracking controller based on quadratic optimal control theory is considering for analysis. Overall performance of the control design is based on Liapunov approach, where quadratic performance index is directly related to Liapunov functions. By minimizing and maximizing the performance index value corresponding to control inputs will trace the tracking error inaccuracies. As maximizing the performance index, the tracking error produces 0.04% inaccuracy. The data loss is 0.06% when minimizing the performance value. Simulation is carried out using Mat lab.
WSN, RFID, Surveillance Integration model, Quadratic Optimal Control
Короткий адрес: https://sciup.org/15010806
IDR: 15010806
Текст научной статьи A Heterogeneous Access Remote Integrating Surveillance Heuristic Model for a Moving Train in Tunnel
Published Online March 2016 in MECS
The train tracking, controlling and monitoring system is an emerging technology in the rail sector. In minimum budget railways, the reliability, accuracy, driver assistance, cost efficient technique, availability and integrity are the major factor. The signaling of train and rail traffic play significant role in the wireless communication solution. Real time information of the train movement in satellite visible areas are acquired from satellite based positioning system [1] [2].These systems are more accurate, precise, efficient, low cost and less economic maintenance. But line of sight between transmitter and receiver as well as multipath loss in the low satellite visible areas such as mountains, tunnel, valleys, deep cuttings etc. completely shadowing information. The navigation information cannot be relay completely on the basis of satellite based positioning systems alone [3]. Some of the expensive surveying technique such as unmanned aerial vehicle surveillance, interferometric synthetic aperture radar, laser scanning can also be used to acquire the geographical data. But these systems are highly restricted with cost, area and duration. The above explained factors enable us to focus on designing sensor based technology. The integration of satellite based navigation system with sensor technology can bring communication diversity [4][5] This paper attempts to build useful approach by integrating Wireless Sensor Network with Radio Frequency Identification system. The sensor network supply us general navigation data where as RFID gives precision information near the targeted object.
Nowadays the use of WSN has been adopted in many applications such as surveillance, measurement of temperature, humidity and other environmental parameters, building maintenance, pollution monitoring etc. WSN technology is very useful for autonomous sensor data collection process. It is a group of heterogeneous sensor nodes capable of sensing, identifying, positioning the objects to monitor and control in distributed manners [6]. In our research it is employed to monitor the rail and its surrounding environment with sensing function rather than identifying the train. To overcome this limitation, RFID is the best choice because it detects and identifies the moving train with precise navigation. By integrating two important wireless technologies like WSN-RFID, it is possible to improve sensing capacity as well as navigation system even more [7]. This is fully automated wireless model located on moving train to provide train’s location, speed, velocity and other parameters. The fused information from sensors is expected to improve the train detection and tracking accuracy in tunnel. One major objective of the fusion technology referred is mainly because each system may compensate for the failure of the other. The current paper explains how information is acquired from fusion model and its tracking control performance is obtained with the help of quadratic optimal control theory. The advantage of using this theory is that the system designed is stable [8]. The wireless tracking controller based on quadratic optimal control theory is considering for analysis. Overall performance of the control design is based on Liapunov approach, where quadratic performance index is directly related to Liapunov functions. By minimizing and maximizing the performance index value corresponding to control inputs will trace the tracking error inaccuracies. As maximizing the performance index, the tracking error produces 0.04% inaccuracy. The data loss is 0.06% when minimizing the performance value. Simulation is carried out using Mat lab.
-
II. Related Work
Many technologies have been implemented for train tracking, controlling and signaling in satellite visible environment. Some presented using Global Positioning System (GPS), Wireless Sensor Network (WSN), General Packet Radio Switching (GPRS), Zig Bee and Radio Frequency Identification (RFID) for intelligent rail monitoring. But in low satellite visible environment, tracking and controlling of train is a major challenging issue. Integration with the sensor technology of user localization in complex environments will provide higher precision results. It solves the pros and cons in each localization technique. To avoid this, author [11] propose a system with GPS, WIFI, RFID and pedometer technology with optimization technique. Increasing the movement speed can mean failing to detect some sensors to provide fast and accurate navigation. Author [12] proposed system by combining WSN and Passive RFID. The sensor network provides fast general navigation in open area and RFID provides precision navigation near static obstacle. The author [13] proposed low cost, low power consumption localization scheme for ZigBee based WSN. Author integrates WSN and ZigBee with cooperative approach, coefficient delta to regulate the speed of convergence of the algorithms and filtering process using extended Kalman filter. Recent advances in WSN with GPS technology are considered by [14]. Author investigates how accuracy of GPS decreases and how to avoid the line of sight and multipath loses in tracking or navigation application. He proposes the conventional statistical test method and differential outlier detection method. With the increasing development of tracking stability, accuracy, real time quality WSN is adopted widely in tracking applications. But some limitations of WSN such as noise, interference, limited bandwidth, power time varying gain, bring the factors of uncertainty, non-linearity, time delay, limited energy to WSN-based control systems. Hence it is an emerging and challengeable research to study tracking control problems. Current research highlighted on tracking control issues in WSN environment. The author [15] designs the fuzzy observer-based tracking control for time delay non-linear distributed parameter system. He highlighted range and range-rate measurement for multi target tracking with uncollected information. Multimodality frame work and n-step predictive tracking algorithm to conserve the energy consumption is explained. After verifying the previous works on tracking control problems with many algorithms, it is challenging to solve the relevant issues. However, some presented on small scale but not for large scale systems and not concerned with the accuracy and precision. Hence the main contribution of this work is to integrates WSN and RFID technology together and propose system which can track the train accurately and precisely.
The organization of the paper is as follows. Section (3) explains the surveillance integration model of WSN-RFID, in which how data are communicated to central office. The model of tracking controller to track the moving train in the tunnel is depicted in section (4). Section (5) describes the problem formulation to track the moving train using Quadratic optimal control theory. The explanation in Section (5.1) is about the selection of performance index and how it depends on the control inputs. The Optimal control design analysis using Liapunov method where performance index is considered as optimization parameter is briefed in section (5.2).Section (6) explains simulation set up using Mat lab. The results and analysis of the moving train position and velocity graph with related control inputs are explained in section (7). Finally section (8) depicts concluding remarks.
-
III. Tunnel Surveillance Heuristic Integration Model of WSN-RFID
The major objective of surveillance system is to track, detect and recognize the moving object in the allocated area. For continuous control and monitoring of train movement in the tunnel a surveillance model is required. Fig.1describes the block diagram of surveillance heuristic model based on wireless technologies such as WSN and RFID. One major objective of the fusion technology referred mainly because each system may compensate for the failure of the other. The fused information from sensors is expected to improve the train detection and tracking accuracy in tunnel. WSN is group of heterogeneous sensor nodes capable of sensing, identifying, positioning the objects to monitor and control in distributed manners. In our research it is employed to monitor the rail and its surrounding environment with sensing function rather than identifying the train. A distributed control algorithm is used for WSN system in which the co-ordination and communication between the interconnected sensors with increase in accuracy. The subsystem consists of sensors which are communicated with each other to exchange data by WSN. In each of these subsystems, base station acts as controller which transfer the command signal to the actuator ensuring it be executed by the node.
RFID system mainly consists of tags and reader. A tag has an identification information and memory that stores additional data. The reader is able to read and write the data from tags. Each tag is equipped with wireless module which can transmit data to the reader. In fact the reader is acts as sensor node which reads the identification of moving train in tunnel. RFID is integrating with WSN in such a way that each tag is connected to sensor. The sensors detect the train location data periodically and independently. The sensing data is transmitted to the reader. The reader is considering as sensor node which reads the identification of train. RFID tag is equipped with a wireless module which transmits data to and from the reader. The information starts to exchange to the data base through the web server.
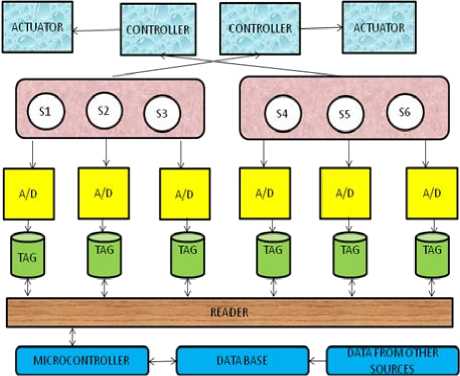
Fig.1. Block diagram of WSN-RFID integration model
-
IV. Tracking Control Design
The integration model of WSN- RFID is used to detect the moving train and its kinematics in the tunnel. We propose the design using digital control system. It is required to place WSN -RFID system upright as much as possible and control the position of the train which is moving in step fashion. To control the position and velocity of the train we need to build type 1 Servo System. Fig.2 shows the block diagram of tracking controller design. The designed control system includes state feedback and an integrator in the closed loop. The control force is applied to the train.
feedback controller. Considering r(k) is the step input where the train is moving in step fashion. The displacement of the train y(k) is the output of the system. The state of system x(k), control input u(k) with system state matrix G [n*n matrix], control matrix H [n*r matrix] are the design parameters.
-
V. Rail Tracking Problem Formulation
The fusion model and its tracking control performance are obtained with the help of quadratic optimal control theory. The advantage of using this theory is that the system designed is stable. The wireless tracking controller based on quadratic optimal control theory is considering for analysis. Overall performance of the control design is based on Liapunov approach, where quadratic performance index is directly related to Liapunov functions. By minimizing and maximizing the performance index value corresponding to control inputs will trace the tracking error inaccuracies. Consider step input as control input in all cases.
Let us now design the quadratic optimal control problem where the process is continues without bound
N=∞
The plant equation is
X (K+1) = A X (K) + B U (K)(1)
Y (K) = C X (K)(2)
V (K) = V (K-1) + R (K) - YK)(3)
V (K+1) = V (k) + R (K+1) – Y (K+1)
= V (K) + R (K+1) – C [A X (K) + B U (K)]
-
= V (K) + R (K+1) – CAX (K) – CBU (K)(4)
U (K) = KI V (K) – KX (K)(5)
Where,
K I = Gain constant and K = Feedback gain matrix
By considering equations (1) and (4), the state model is written as
Х(К - 1)
У (К 4-1)
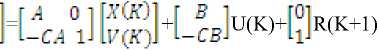
By defining,
r(k) u(k) x(k)
y(k)
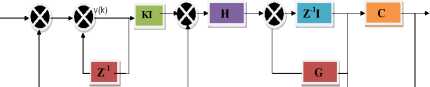
INTEGRAL CONTROLLER
Fig.2. Block diagram of tracking controller (servo system) design
А=И 0
Ầ =
| B^ = [_|5] K^ = [ K, -K I ]

STATE FEEDBACK
Now consider the quadratic optimal control problem where the process is continuous with K=∞.
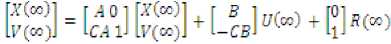
Design variables are gain constant (KI) of integral controller and feedback gain matrix (KF) of state
The error can be calculated by considering equation (6)
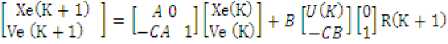
Assuming that the input R (K) is step function.
R (K) = R (K+1) = R
By defining,
X e (K) = X (K) - X(∞)
V e (K) = V(K) – V(∞)
Хе(К + 1)"
U e (K)=KX e (K)+K e (K)=-[К - KI] Ve(K + 1) (8)
-
5.1 The Nature of the Performance Index (J)
For the designing of an optimal control system a best attainable performance index ‘J’ is chosen. Depending on the requirements of the system, the value of performance index must meet and determine the nature of resulting system. The purpose of using it is to maintain the stability of the system. The system behavior is optimized by choosing control vector U (K) in such a way that the performance index is minimize or maximized.
When optimal control law is applied,
U (K) = - K X(K) (9)
The Performance Index related with steady state optimal control law
J=1/2 I^=D[X- (ЮЕХ(к) + u* GOFUGO] (10)
Where
E = n x n positive definite or positive semi definite Hermitian Matrix.
F = n × r positive definite or positive semi definite Hermitian Matrix.
(The necessary condition for Hermitian matrix form is X*AX)
In this optimization problem, the values of E and F matrices are choosing the quadratic performance index which in turn depends on State vector, Control vector and final state.
-
5.2 Quadratic Optimal Control Problem analysis using Liapunov method
There are several methods to obtain the steady- state solution of the optimal control problem. There is a direct relationship between the quadratic Performance Index and Liapunov functions.
Consider an optimal control problem where the plant equation (1), optimal control law (9) and Performance Index (10) are modified for minimization.
X (K+1) = AX (K) + B [- K X (K)] = AX (K) – KBX (K)
X (K+1) = X (K) [A-KB](11)
J=1/2 £”=0[Х»(ЮЕХ(Ю + и* (Юги(Ю]
=]
J = 1 /2 I”=0[Х * (Ю (Е + К * FK }]Х(К)](12)
For the parameter optimization, the matrix A-KB is stable and the Eigen value of this matrix will lie inside the unit circle. For the system of equation (1), a Liapunov function is defined by adjusting the parameter in order to minimize the performance index.
V{X (K)} = X*(K) PX (K)
Where P is positive definite Hermitian matrix and whose derivative is negative definite.
dV/dk (X(K)) = V{ X(K+1)} – V{X(K)}
= X* (K+1) PX (K+1) – X*(K) PX (K)(13)
Applying equation (13) in to Equation (12), we get
X*(K) {E+ K*FK} X (K) = - [X* (K+1) PX (K+1) –
X*(K) PX (K)](14)
Substituting equation (11) in above equation (12),
X*(K) { E+ K*FK}X(K) = - [ (A-BK)X(K)]* P[(A-BK)X(K)+X*(K) PX(K)]
= - X*(K) [(A-BK)* P [(A-BK) - P] X (K)](15)
Comparing both sides of the above equation,
E+ K*FK = - [(A-BK)* P [(A-BK) - P]](16)
E+ K*FK + (A*- B*K*) P (A-BK) – P = 0
E+ K*FK + (A*P - B*K* P) (A-BK) – P = 0
E+ K*FK + A*PA –A*PBK- B*K*PA +B*K*PBK –P =0
Hence it is further modified as,
E+ A*PA-P + [(F+B*PB) 1/2K – (F+B*PB)-1/2B*PA] [(F+ B*PB) 1/2K- (F+B*PB)-1/2B*PA] – A*PB (F+B*PB)-1B*PA =0 (17)
The Performance Index is minimizes with minimize in the value of matrix K,
[(F+B*PB) 1/2K – (F+B*PB)-1/2B*PA] [(F+ B*PB) 1/2K-(F+B*PB)-1/2B*PA]
Is zero or is non-negative.
(F+B*PB) 1/2K = (F+B*PB)-1/2B*PA
K = (F+B*PB)-1 B*PA (18)
Substitute equation (18) in to equation (17),
P= E+A*PA- A*PB (F+B*PB)-1B*PA (19)
By using Identity matrix I, the matrix P can be reloaded as,
P= E+ A*P (I+BF-1B*P)-1 A
The minimum value of Performance Index J is obtained as follows from equation (14)
J = 1 /2 I”=0[X * (Ю (E + К * FK }]X(K)]
J = 1/2 Ʃ∞ k=0 [X* (K+1) PX (K+1) –X*(K) PX (K)]
Design approach
-
• Insert an integrator in feed – forward path.
•Control force ‘u’ is applied to the train.
•Position signal ‘Y(k)’ is connected back to the input.
•Consider discrete time control system
-
• X(k+1) = G X(k) + H U(k)
•Optimal control vector will maximize the performance index
-
• J= ½ X*(N) SX(N) + ½ [ X*(k)QX(k)+ U*(k) RU(k)]
-
• Determine the feedback gain matrix.
•Determine Optimal control vector U(k).
•Determine integral gain constant.
-
• Output of the integrator.
In the optimization process, the performance index and control input parameters are considered equally important. By minimizing and maximizing the performance index value corresponding to control inputs will trace the tracking error inaccuracies. Consider step input as control input in all cases and calculate how much data loss is produce when the train is moving in tunnel.
-
VI. Simulation Results
To verify the performance of the WSN-RFID based tracking controller design, various simulations is conducted for different values of performance index corresponding control inputs. The simulation is carried out using Mat lab.
Case 1. Considering optimal control input U (K) = -0.7913, Performance Index J = 0.5. Figure.3 indicates the control input history to provide acceptable tracking performance. From Fig.4 it is evident that the calculated state velocity is almost closer to the reference state value. Fig.5 shows the simulation results of position of train moving and its corresponding state error. By maximizing the performance index to some extent we could improve the response even more. It concludes that the data loss is less and produces 0.006% inaccuracy. The train’s final position is also not close to the desired location but has in fact travelled in opposite direction.
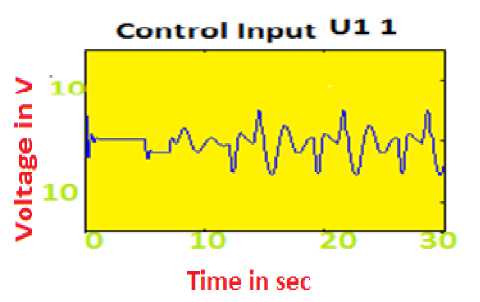
Fig.3. Control input U(K)=+ 0.7913is applied when the train is moving
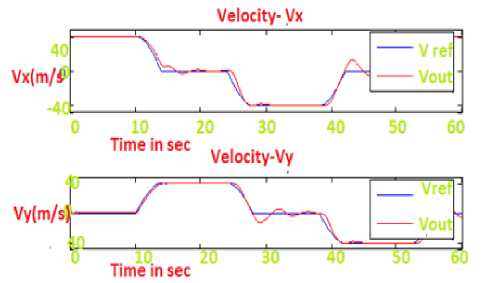
Fig.4. Velocity of train When moing along X, Y and its tracking error.
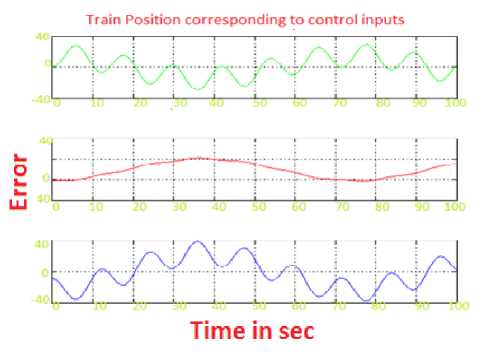
Fig.5. Train along X, Y Position and its tracking error.
Case 2.Considering optimal control input U (K) = -0.2087, Performance Index J = 1.8 Figure.7 indicates the control input history to provide acceptable tracking performance. From Fig.8 it is evident that the calculated state velocity is almost closer to the reference state value. Fig.9 shows the simulation results of position of train moving and its corresponding state error. By maximizing the performance index to some extent we could improve the response even more. It concludes that the data loss is less and produces 0.004% inaccuracy. The train’s final position is also not close to the desired location but has in fact travelled in opposite direction.
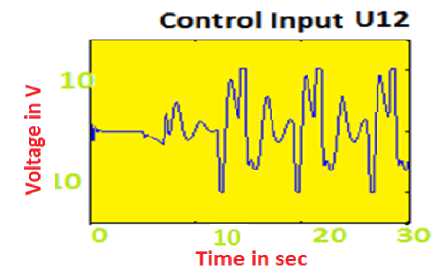
Fig.6. Control input U (K) = - 0.2087 is applied when the train is moving
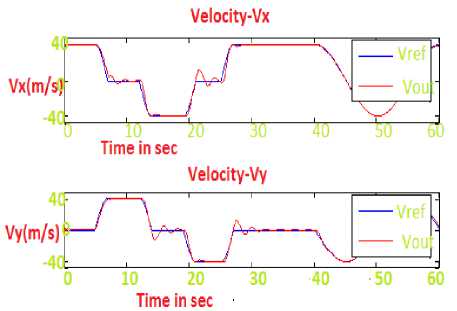
Fig.7. Velocity of train When moing along X, Y and its tracking error.
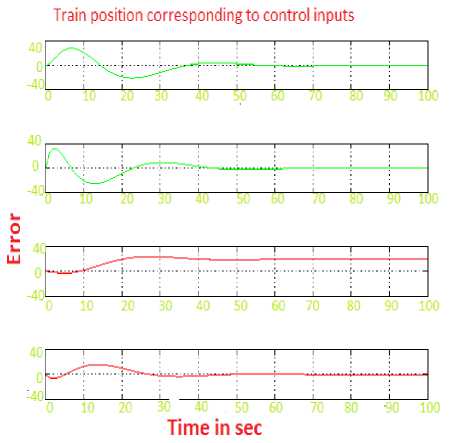
Fig.8. Train along X, Y Position and its tracking error.
From the two cases finally it is conclude that, the initial track observations is run for 60 samples. If we create a model based on the true situation, our estimated state will be close to the true position value. The state errors in X and Y position are inverse to each other. When the train along X direction then position state error is +0.5 at t=30 and -1 at t=35. Similarly along Y direction position state error is +0.5 at t=3, 40. From these graphs we conclude that the data loss is more, when the train tracks along X direction and produce only 0.005% inaccuracy. In the graph it is shown that the estimated velocity is getting close to the true value and has less error than measurement noise. There is no much variation along X direction but is very noticeable along the Y direction as expected.
Tracking error comparison
Table.1. Tracking error comparison
|
Case |
Velocity |
Position |
||
|
V x |
V y |
P x |
P y |
|
|
1. U(k)= 0.7913 J= 0.5 |
0.2 |
-0.2 |
0.4 - |
0.4 |
|
2. U(k)= -0.2087 J= 1.8 |
0.5 |
-0.6 |
0.6 |
-0.5 |
The numerical comparison of tracking performance error is shown in Table.1 It shows that the errors are calculated from the true and reference path values. The tracking performance errors in case 1 is lower compare to case 2.
-
VII. Conclusion
In this paper a tunnel surveillance model designed by integrating WSN –RFID. The design analysis is based on quadratic optimal control theory is elaborated. Liapunov method is formulated to find the optimization parameter. It has been demonstrated that when a train is moving in the tunnel with constant and varying velocity results in data loss of only 0.003% inaccuracy. Simulation is carried out using Mat lab.
Список литературы A Heterogeneous Access Remote Integrating Surveillance Heuristic Model for a Moving Train in Tunnel
- U.S. Coast Guard Navigation Centre, NAVSTAR GPS user equipment introduction (Aug 1, 2011)
- AGUADO, L, et al:”A low Cost Low Power GPS Positioning system for monitoring Landslide “ NAVI Tech 2007
- Will HEDGCOCK et.al” High accuracy difference tracking of low cost GPS receive “,Elsevier 2011
- M.A.HANNAN et.al” Intelligent bus monitoring and management system”. IEEE vehicular communication journal, 2012
- X, Lieu and A. Goldsmith, “ Wireless Communication Tradeoff in distributed Control”, in Proceedings of the 42nd IEEE Conference on Decision and Control, PP 682 – 694, Dec. 2009
- Oka and L, Lampe, “Distributed Target Tracking signal Strength Measurement by a Wireless Sensor N L. IEEE Journal on selected areas in Communications, Volume, 28, No 7 PP 1006 – 101, 2010
- Zhang, and Z. Wang, “Integration of RFID into Wireless Sensor Networks: Architectures, Opportunities and Challenging Problems”, Proceedings of the Fifth International Conference on Grid and Cooperative Computing Workshops (GCCW'06), 2006.etwork”,
- M. TABBARA, D, NESIC and A. RTEEL, “ Input output stability of Wireless network control systems” In Proceedings of the 44th IEEE conference on Decision and Control, and European Control Conference, PP 209 – 214, Dec. 2005
- A. Budiyono, “Principles of optimal control with applications.” Lecture Notes on Optimal Control Engineering, Department of Aeronautics & Astronautics, Bandung Institute of Technology, 2004.
- Zehang Sun, George Bebis, and Ronald Miller, “On-Road Train Detection: A Review” IEEE Transactions On Pattern Analysis And Machine Intelligence, Vol. 28, No. 5, May 2006
- A. Oka and L, Lampe, “Distributed Target Tracking signal Strength Measurement by a Wireless Sensor Network ”, IEEE Journal on selected areas in Communications, Vol, 28, No 7 PP 1006 – 101, 2010
- M.Tabbara, D, Nesic and A. Rteel, “ Input output stability of Wireless network control systems ” In Proceedings of the 44th IEEE conference on Decision and Control, and European Control Conference, PP 209 – 214, Dec. 2005
- Y.Sun, S, Zang, H.Xu and S. Lin “Cooperative Communication for Wireless Ad hoc Sensor network”, International Journal of distributed sensor network Vol 2013, Article ID 161268, 2 pages 2013
- W. Chen, and Y Fu “Cooperative distributed target tracking algorithm in mobile wireless sensor network” International Journal of Control Theory and Applications, VOl. 9 No. 2 PP 155 – 164, 2011
- Y.T. Cheg and B.S. Chen, “ A Fuzzy Approach for Robust reference tracking control design of nonlinear distributed parameter time delayed systems and its applications” IEEE Transactions on Fuzzy Systems, Vol. 18, No.6 PP 1041 – 1057, 2010
- Saad Chakkor, El Ahmadi Cheikh, Mostafa Baghouri, Abderrahmane Hajraoui ‘’ Efficiency Evaluation Metrics for Wireless Intelligent Sensors Applications’’ International Journal of Intelligent Systems and Application, Volume 6 No 10, October 2014, Mecs Pess Publisher


