A High Performance Image Authentication Algorithm on GPU with CUDA

Published Online March 2011 in MECS

Digital images are widely distributed today over the internet and through other mediums, and there are powerful digital image processing tools which have made perfect image duplication a trivial procedure. Therefore, copyright protection and integrity verification of digital image have become an urgent issue in the digital world. Image authentication technology is important in various types of images’ protection. A vast research has been conducted on methods of image authentication, and many useful concepts such as signal transform (DCT, DWT, etc.) and HVS (Human Visual System), was employed to improve the performance and to satisfy the practical requirement. As a result, lots of the algorithms proposed in literatures are complicated in computation, which restrain their being adopted in some real-time occasions. Improving the efficiency of image authentication process has become one of the challenges in this field.

Some researchers have used hardware like FPGA and custom IC as co-processor in image processing, but the procedure of hardware designing and programming is not

Corresponding Author: Lei Zhao a friendly work. On the other hand, nowadays, GPU devices are wildly equipped in personal computers and have a great potential in mass parallel computing capability. Traditional GPGPU (General Purposes Graphical Processing Unit) methods, however, require programmers equipped with graphic knowledge and API, which make the work of designing of GPU parallel computing tedious and hard to debugging. As the release of NVIDIA’s Compute Unified Device Architecture (CUDA), researchers can design programs for both CPU and GPU conveniently with a C-like programming language, without knowing fundamental knowledge on computer graphics.

In this paper, we firstly propose an image authentication scheme, and then discuss the implementation of it on CUDA-enabled GPUs, which have been widely equipped in today’s PCs. Experimental results show that our CUDA-based method for image authentication gains a good performance in both authentication results and operation speedup. The rest of this paper is organized as follows. Related work is discussed in Section II. In Section III, the hardware model and programming model of CUDA is reviewed. And the image authentication algorithm proposed in this paper is presented in section IV. Section V describes the detail of CUDA-based implementation of the proposed algorithm, and experimental results of the implementation are presented in Section VI. Conclusions are drawn in Section VII.

• II.    R ELATED WORK

Generally speaking, image authentication techniques can basically be categorized into two types: digital signature and digital watermarking [1]. Extensive research on image authentication algorithms have been proposed in the last decades, especially on semi-fragile watermarking. Semi-fragile watermarking technology is mainly used for image content authentication. It is required that the authentication method is able to tolerate incidental manipulations while being sensitive to malicious distortions.

Chen proposed an image authentication scheme combines digital signature and watermarking [2], which extracts signature from the original image and embeds them back into the image as watermark and avoid additional signature bandwidth for transmission, the algorithm shows not only tolerate JPEG compression but also able to locate the illegal modifications. Ho and Li [3] proposed a semi-fragile watermarking scheme which tolerates JPEG compression and equipped with the properties of nondeterministic block-wise dependence, obliviousness and localize attacks. Lin and Su present a semi-fragile method by employ a new concept of the lowest authenticable JPEG quality (LAJQ), and also prove the validity of pre-compression method mentioned in literatures [3-5]. The scheme in [10] took HVS into account to against special attack of watermarked images. Other schemes can not only localize the modifications, but also recover the tampered region [11].

Although these methods performed well in image authentication, most of them need computational intensive operations, and thus are unable to generate a result instantaneously. Several hardware assisted methods for digital signature and watermarking acceleration have been studied in recent years, for instance, some attempts for accelerating watermarking methods by using dedicated special-purpose hardware like digital signal processor (DSP) and field programmable gate array (FPGA) [6], for example, [14] proposed robust and fragile watermarking acceleration schemes by using custom IC hardware, and Seo and Kim presented a FPGA co-processed method for robust watermarking in DWT domain [15]. Nevertheless, these methods are designed at the hardware level that limit the capability of programming, thus designing different schemes may require complete changes of hardware architectures. What’s more, these devices are not commonly available in consumer level PC, which constraints the deployment of related technology. Graphics Processor Unit (GPU) is one of high performance computing platforms and wildly available in today’s PC. Brunton and Zhao [7] used GPU as a co-processor, and proposed a watermarking-based content authentication method for real-time video application, and the system was shown to have good performance both on processing efficiency and authentication results. Mohanty [8] presented an efficient, real time and low cost watermarking system for image, by implementing a dedicated processor chip as a coprocessor for the GPU. However, their methods are still focused on hardware designing or required knowledge on graphics API or dedicated processor chips. On the other hand, the new release of GPU programming platform CUDA [9] offers highly parallel computation and flexible programmable environment. Many recent papers have devoted to exploiting the massive parallel computing processors on GPU’s massive cores, and lots of problems in the fields of linear algebra [16], image processing [17], biomedical information [18], signal processing [19], etc., have benefited from its speed and parallel processing capability. However, seldom CUDA-based accelerating watermarking or image authentication methods have been presented in literatures. The goal of using CUDA in image authentication field is to establish a high performance, real time, flexible and ease developed system of authentication.

• III.    CUDA OVERVIEW

Compute Unified Device Architecture (CUDA) is a new hardware and software architecture for designing and dealing with computations on the GPU, without the need of mapping them to a graphics API, and allow direct access to GPU processors and device memory. Its straightforward extension of the C programming style and native interface to GPU’s data-parallel model have made the implementation of GPU-based parallel computation a friendly work [9]. However, to achieve high performance, software designers need to acquire knowledge about CUDA’s architecture and programming optimize strategy.

• A.    Hardware Model

  The CUDA device is equipped with a set of SIMD stream multi-processors (SM), and each SM contains several stream processors (SP). For example, NVIDIA Tesla C1060 GPU is build with 240 SP cores, organized in 30 SM streaming multiprocessors. GPU’s massive process cores make it naturally to run great amount of concurrent threads at the same time. As a result, GPU is suitable for data-parallel and computing intensive tasks.

CUDA architecture provides access to several types of memory. Global (device) memory can be read and written by all threads. For each thread block, there is a shared memory (on-chip memory) available for all threads within the block, and registers are local storage for each SP. Share memory has low access latency and high bandwidth, similar to an L1 cache. Thus, the access speed of shared memory and register are much faster than global memory, so it is an important strategy for accelerating data access. There are also two additional read-only memory spaces accessible for all threads: the constant and texture memory spaces. Texture memory is a special case of device memory which is cached for locality. Constant memory is cached memory that can be written by the CPU and read by the GPU. To achieve highest throughput, consecutive memory locations must be simultaneously accessed by the threads, which is called memory access coalescing. By coalescing the global memory reads and writes, and avoiding on-chip shared memory bank conflicts, performance gains can be further increased. This is an effective technique for hiding memory latency and will be taken into account in our later implementation.

• B.    Programming Model

Under the CUDA programming model, applications are divided into grain independent tasks. These tasks are parallelized by scalar execution units called threads. A set of threads are organized as thread blocks, and each thread and block is given a unique ID that can be accessed within the thread during its execution. The CPU invokes the GPU by calling a CUDA kernel. In fact, kernel is a special C function. In a given execution of CUDA kernel, each thread can perform the kernel task on different set of data using the thread and block IDs. The set of all blocks run during the execution of a CUDA-kernel is called a grid.

Threads within a block can share data with each other. Besides, it’s able to place synchronization points to control the execution flow of all the threads within a block. Threads from different blocks in the same grid can coordinate only via operations in a shared global memory space visible to all threads. This provides fine-grained data parallelism and thread parallelism. 16 consecutive threads in a block form a half-warp, and 2 half-warps form a warp. A warp size of consecutive threads which take the same execution path will be activated at the same clock cycle of GPU. Thus, threads in a warp that execute different task paths (also called diverge) must wait in turn for the next executing clock cycle. Therefore, it is highly suggest avoiding divergence in a warp to achieve substantial efficiencies of processors.

• IV.    IMAGE AUTHENTICATION ALGORITHM

In this section, we propose a semi-fragile watermarking algorithm for image authentication. The algorithm extracted features from low and middle frequency domain of DCT coefficient blocks and embedded them into high frequency region.

• A.    Review of DCT

Discrete Cosine Transform (DCT) is a transformation function which transforms the representation of data from space domain to frequency domain. DCT method is well known in image processing for it’s used in the standard of

JPEG compression. As for matrix I M _x N , 2-dimensional

DCT formulate is defined as follow:

C ( u , v ) = ^{d (} u ) 5 ( v ) y^ I ⁽ i , j ^)cos[ ^{n (2}2^ 1) u ]co^{s[ n (2} j ^ 1) v ^{] (1)} 1= 0 j : 0            2 M          2 N

And the corresponding inverse DCT formulate is:

I ⁽ i . j ) XX ^{d (} u ^{) d (} v ) C ⁽ u ^, v )c^os[ ^{n (2} it, 1) ^{u ]}c^os[ ^{n (2} j + 1) v ^{] (2)} u = 0 t0                   2 m         2 N

Where

d( u ) :

<

u : 0

, d(V) = u * 0

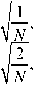
V = 0

,0 <  u <  M -1,0 <  v <  N -1 v * 0

• B.    Feature extraction and embedding scheme

The steps of image feature extraction and embedding are expressed as follows:

• 1)    Performing block-based DCT

Divided the original M x N image I into nonoverlapped 8 x 8 blocks, where i, j are locations of the blocks in image I , and apply 2D-DCT to each block, then we get DCT-coefficient blocks C (suppose the i,j whole block-wise DCT-coefficient matrix is C ). For each 8 x 8 DCT-coefficient block, the well known zigzag order is employed, and each block is partitioned into low (L), middle (M), high (H) frequency domain, as illustrated in Fig.1.

• 2)    Secure serial-numbers generation

To increase the security of the algorithm and avoid block-wise independence, we employ the Logistic chaotic model and generate a unique serial-number T(i, j, д) for each block C using the following equation: i,j xn+1 = Mxn (1- xn )               (3)

where д (3.5699 <  д <  4) is an initial private key.

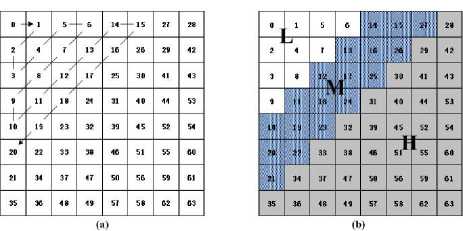
Figure 1. (a) Zigzag order of 8×8 DCT-coefficient block; (b) Frequency domains 8×8 DCT-coefficient block.

• 3)    Watermark extraction

The watermark sequences extracted from image are invariant relationship between two DCT-coefficients in 8 x 8 block pairs, which was proved to be robust before and after JPEG compression by Lin and Chang [5]. Thus, we will employ this property to extract image features. In order to make later expression clearer, let us take the neighboring block C _{0, 0} and C _{0, 1} for example, and we define the following symbols:

• •    K l , K m : tow dynamic secret keys used to pick

the positions from the low and middle frequency domain, and they are defined as below:

K l : A l Ф T (0,0, д ) Ф T (0,1, д )

K m : A m ® T (0,0, д ) Ф T (0,1, д )

where At and Am are another two private keys, and T(i, j, д) is a serial-number generated by (3). •    ls: the zigzag order indexes of four coefficients picked from the low frequency domain by Kl , s ={1,2,3,4};

• •    m s : another four indexes picked from the middle

frequency domain with private key K_m ;

Then the low frequency feature vectors W_L ¹ and W_L ² are extracted using the following rules:

_W s ) _: (1 C 0,0 ( l s ) <  C 0,1 ( l s )

L ^ { 0 otherwise

_W 2 _{( s} ) _: fl sign ⁽ C 0,0^{( l}s )) * sign ⁽ C 0,1^{( l}s ))

L     {0 otherwise and the watermark vector generated from low frequency domain can be defined as:

W L : W L ¹ Ф W L

Similarly, for the middle frequency domain, we have:

W 1 ( V ) = I¹ C 0,0⁽ m s- ) ^- C 0Д⁽ m s )

M^    {0 otherwise

W 2 ( s ) = P sign ^{( C} 0,0⁽ m s )) * sign ^{( C} 0,1 ( m s ))

M^ ’ {0 otherwise

And define the watermark vector of middle frequency domain as follow:

WM = WM © WM          (5)

As a consequence, we completed watermark extraction from block pair: C0, 0 and C0, 1 . The similarly processing will be done for the other block pairs.

• 4)    Embedding watermark

The step of embedding watermark, we take the partial high frequency domain as watermark embedding region Em. Fig.2 (a) shows the embedding region of each 8×8 block. It is in order to ensure the perceptible quality of the image. By pre-quantize the DCT coefficient with a predetermined quality factor [4] [5], the watermarked image will tolerate any number of further compressions of smaller quantization steps. Here we take Q /4 as the quantization table whose elements are corresponding values equal to 1/4 times of the values from JPEG quantization table Q , which is illustrated in Fig.2 (b).

6	1	5	s	14	15	21	21		16	11	10	16	21	«	51	61
2	1	r	13	16	26	25	<2		12	12	14	IS	26	51	50	55
3	8	12	H	25	30	41	43		14	13	16	24	40	57	69	56
9	11	18	24			44	53		14	ir	22	29	51	87	80	62
10	19	23	32			52	54		18	22	37	56	68	109	103	T7
20	22	33	38	46	51	55	60		24	35	55	64	81	104	113	92
21	M	M		st	S6	55	61		15	61	11	81	103	121	120	101
35	36	48	49	57	58	62	63		79	92	95	98	112	100	103	99
(a)									(b)

Figure 2. (a) The region for embedding watermark; (b) JPEG quantization table Q

Still, take C _{0, 0} and C _{0, 1} for example, four coefficients will be picked out from Em region in each block with a private key K_h , which can be got by the ruler below:

K h ( i , j) = Л © T ( i , j , M )

where Ah here is also a private key. Let h, hs means the indexes of the four embedded coefficients inC0, 0 andC0,1 . And C0, 0(h11) and C0, 0(h21) will be embed the first two elements of the watermark vector W∞ L , and C0, 0(h31) , C0, 0(h41) will be embedded the first two elements of the watermark vector W∞ M . Another two elements of W∞ L and W∞ M will be embedded into C0,1(hs2) ( s =1… 4) respectively. Then, we define the following symbols:

RC,/h k ) = round ( C j h k )/ Q ( h s )) k   kk

^URC_M ^{( h} s ) = C .,, ^{( h} s ) / Q ^{( h} s )

Sgn =

• 1    if ( URC i,j ( h k ) - RC, j ( h k )) > 0

• - 1 otherwise

where Q ( h _s ^k ) is the h_s^k th element of Q in zigzag order. Also we define two cases:

• case1 :    W l ( Index ( h^k _s )) = LSB ( RC, , j ( h^k _s )|)

• case 2:    W m ( Index ( h^k _s )) = LSB (| RC, , j ( h^k _s )|) here Index ( ■ ) means the corresponding index of watermark vector and LSB ( ■ ) denotes the least significant bit. The embedding strategy can be expressed as:

• (a)    For s = {1,2} , embbeding W l ,

k   /RQj(hks)xQ(hks)    if case1i,j( s) [(RQj(hks) + Sgn)xQ(hk) else

• (b)    For s = {3,4} , embbeding W m ,

С (h= /RCi,j(hk)x Q(hk)    if case2

-,j( s) [(RQ/hk) + Sgn)xQ(hk) else

After all the blocks of the coefficient matrix C are watermarked, performing IDCT to the watermarked coefficient matrix and we get the watermarked imageIW .

• C. Procedure of Authentication

The procedure of authentication can be performed without the reference of original image, thus this *

algorithm is obliviousness. Assume I is the watermarked image under attack at the receiver end. The authentication scheme can be describe as follows:

*

• • Firstly, processing the image 1 with the same steps performed in the feature extracting, and get **

the watermark vectors W ^∞ L , W ^∞ M from block pairs. Also, extracting watermarking W ^∞ H from high frequency domain in each block. Verifying the embedded coefficients of block C ^* as i , j follows:

• (a)    For s = {1,2} ,

_{Ver (} C * _{( h}k )) = /0 if W L ( Index ( h k )) = W H ( Index ( h k ))    (8)

^V’^jVsn   [1 else

• (b)    For s = {3,4} ,

• _Ver ( C * ( _hk )) = / 0 if W M ( Index ( h k )) = W H ( Index ( h k )) (9) ‘ • j ^s      [ 1 else

• • Then the integrity of each block can be authenticated with the following rule (9), and C ^*     will be marked as “invalid”

i,j if Auth(C*j) > 3, otherwise marked as “valid”.

The authentication result of this scheme will be show in the latter section.

Auth ( C j = £ Ver ( C*^ h S ))       ⁽¹⁰⁾

s = 1

• V.    CUDA- BASED I MPLEMENTATION

• A. Details of Watermarked Image Generation with CUDA

Looking into the image authentication algorithm proposed in section IV, we can find that the amount of calculation of the algorithm centralized on the process of DCT and watermark extracting and embedding, which are highly amenable to parallel processing. Thus parallelizing these processing will accelerate the performance of the algorithm considerably. The CUDA-based watermarked image generation will be implemented with a CUDA kernel function named CuAIG-Kernel, as illustrated in Fig.3.

The CuAIG-Kernel is implemented on a grid of M /32 x N /32 thread blocks, and each block consists of 8 x 4 x 4 threads. The implementation of CuAIG-Kernel is described below.

For computing partition, we firstly further divided the DCT coefficient Matrix C into 4 x 4 non-overlapped macro-blocks, namely each macro-block consists of sixteen 8 x 8 blocks, as showed in Fig.4.

In the executing of DCT, we decompose the task into series of macro-blocks, and they are mapped into equal numbers of CUDA blocks, that is one thread block is

8 x 8 blocks. As the equation (10) showed, the performing of 2D-DCT on sample X can subsequently

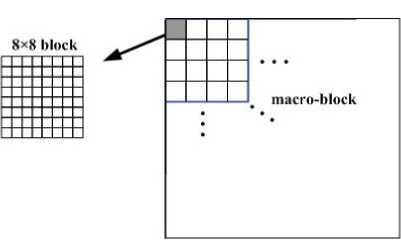
Figure 4. Divide block-wise matrix into non-overlapped macro-blocks apply DCT to columns (Y = AT X) and rows (C = YA ) of the input signal:

C ( u , v ) = ( A T X ) A             (11)

where A is an 8-order cosine matrix, X is a 8 x 8 block. To make the DCT-computing of each block even more efficiently, we also employed the high redundancy and symmetry of the elements of matrix A . More detail can be seen in [11].

While performing the step of watermark extracting, 8 threads as showed in Fig.6 (a) involved to generate watermark vectors W ^∞ L and W ^∞ M by the rule defined in section IV.

Host(CPUi

Device (GPU)

Loading original image data

Set execution configuration of CuAIG-Kernel

Launch Kernel

Prepare original image data for on-chip memory

Perform block-

Data collection and source preparation

Return:

data :

CuAIG-Kernel

corresponding pix

Write back watermarked image data to global memory

Extract image features and generate watermark

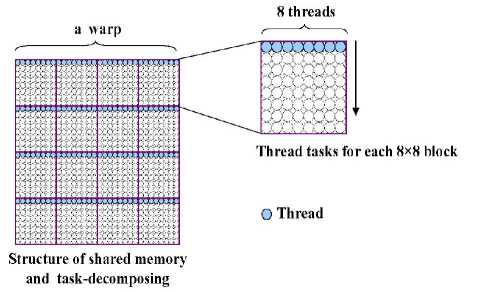
Figure 5. Structure of shared memory and thread-tasks decomposing in each thread block of CUDA

Perform biock-

Eembed

wise 1DCT to each ^_ watermark into

corresponding pix

blocks

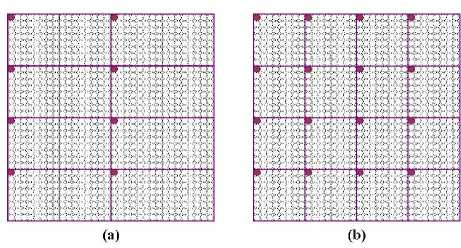
Figure 6. (a) 8 threads involved in watermark extracting; (b) 16 threads involved in watermark embedding

In the step of embedding watermark, 16 threads will be involved to embed several elements of the previous watermark with the rules of (6) (7), as illustrated by Fig. 6 (b). After all watermark elements are embedded, all threads of each CUDA block are involved in performing inverse DCT (IDCT) to the block-wise coefficients and got the final watermarked image data.

At last, all threads are involved to write all of the DCT-coefficients back to global memory with the inverse procedure of reading.

• VI.    E XPERIMENTAL R ESULTS

  In this section, we will present the experiment results of the proposed algorithm for image authentication on both CPU and GPUs. As for the CPU implementation, the algorithm is implemented by using primary-optimized single-threaded C language. Both CPU and CUDA implementations of the algorithm have been performed under a workstation computer equipped with two NVIDIA Tesla C1060 devices. The host’s parameters are showed in Table I and Table II shows the main properties of NVIDIA Tesla C1060.

TABLE I.

MAIN CONFIGURATION PARAMETERS OF TEST ENVIRONMENT

Parameters	Values
CPU	Intel Xeon 5520 (2.26GHz)
RAM	12GB DDR3 (1333MHz)
GPU Architecture	Tesla C1060
OS	Centos 5.3 (64 bit)
CUDA	V2.3

TABLE II

PROPERTIES OF NVIDIA TESLA C1060

Parameters	Values
Number of multiprocessors	30
Number of cores	240
Global Memory	4 GB
Shared Memory per block	16 KB
DRAM	4GB
Registers per block	16384
Clock Rate	1.3 GHz

• A.    Results of Authentication

In the experiment of image authentication, we choose three BMP format image (Lena, Pepper, and Baboon) to demonstrate the effects of the proposed algorithm both on CPU and GPU.

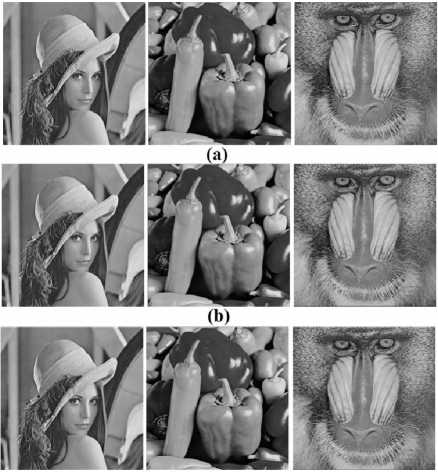
• a)    Imperceptibility

Fig.7 shows the original images and the results of watermarked images on CPU and CUDA version, which fit the imperceptibility as we expected. Table III displays the average PSNR (db) of CPU-processed and GPU-processed Images (512×512 size), and also compare with Lin’s related work [13]. Fig.8 shows the PSNR values of GPU-processed Images in varied sizes.

• b)    Localization of tampering

Fig.9 shows the detected results of the tampered-images (512×512 size) using CUDA version, from which we can see the accurately locating of tampered regions with the proposed algorithm.

• c)    Tolerance of JPEG compression

Fig.10 illustrates the watermarked image undergoing different scales of JPEG compression and their respective authentication results. When the compression scales under the pre-quantization value, authentication results come out be resisting the compression and stay integrity with images before authentication.

• B.    Performance of CUDA-based Parallelization

  To illustrate the accelerating performance of CUDA, we compare the executing time of the proposed CUDA method with CPU version, both executing time of CPU and CUDA version are average values of experiment results in 10 times' running. The speedups achieved with the proposed CUDA implementation range from 20x (512×512 size) to 50x (8192×8192 size), as illustrate by Fig.11.

To make full use of the computing resource of GPU devices, the algorithm was also implemented on multiple GPUs. Two NVIDIA Tesla C1060 devices are involved in the batch processing of images (1024×1024 size).

(с)

Figure 7. (a) Original images; (b) Watermarked images generated by CPU version; (c) Watermarked images generated by CUDA version

TABLE III

PSNR OF CPU-PROCESSED AND CUDA-PROCESSED IMAGES

	Lena	Pepper	Baboon
CPU	39.26	39.36	38.77
GPU	39.24	39.26	38.65
Lin[12]	37.38	36.97	40.52

Table IV shows the executing time of watermarked processing on CPU, single GPU and dual GPU with different amount of files, and we can see that the system gains higher work efficiency with two GPUs than single GPU.

• VII.    C ONCLUSIONS AND FUTURE WORK

39.8 39.6 39.4 39.2 38.8 38.6 38.4 38.2

An image content authentication algorithm is presented and its CUDA-based parallel implementation is also presented in this paper. Experimental results have shown that the performance of the scheme is effective both in authentication results and operations speedup. And further more, multiple GPUs implementation are also employed to make full used of the GPU devices, which works 1.2x times faster than single GPU method. The study of this paper is mainly focuses on acceleration of the image authentication scheme with a novel CUDA-based manner. It is truly that the proposed authentication algorithm can be improved to make it more robust to unintentional manipulation and even be able to recovery the tamper region. Future work involves a more in depth analysis of the optimizations and parallelization strategy of CUDA program in order to further exploit the high performance of GPU’s computation capability, and also extending the CUDA-based method to authentication method within wavelet transform domain.

A CKNOWLEDGMENT

The paper is supported by National Natural Science Foundation of China (No. 61073061). The authors are grateful to all the people for helpful suggestions. The authors would like to thank all the anonymous reviewers for their helpful comments on earlier drafts of this paper.

□ lena

512×512

1024×1024        2048×2048

Image Size

(d) 2Q scale corn press

Figure 10. Different scale of JPEG compression of watermarked images and respective authentication results

Figure 8. PSNR of GPU-processed images in varied sizes

Figure 9. (a) Modification-attacked image and detected result by

CUDA version; (b) Collage-attacked image and detected result by CUDA version

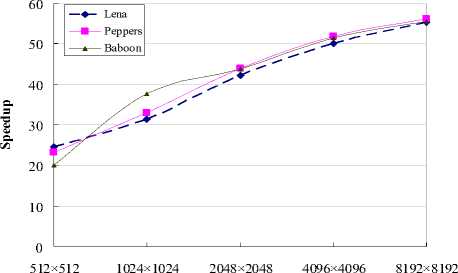
Image Size

Figure 11. Speedup of the generation of watermarked images on GPU compared with CPU version

TABLE IV

EXECUTING TIME OF DIFFERENT NUMBERS OF IMAGES

Computing device	Executing time (msec)			Speedup vs. CPU
	Number of Images (1024×1024 size)
	500	1000	2000
CPU	7153.62	14291.22	28877.66	--
Single GPU	220.53	440.85	903.83	32x
Dual GPU	179.37	378.60	646.27	40x