A Hybrid Algorithm for Privacy Preserving in Data Mining

Published Online July 2013 in MECS DOI: 10.5815/ijisa.2013.08.06

Technology advances in hardware and software have led to increased storage capabilities. With the proliferation of information about individual’s personal data available in the internet and databases, data mining is considered as a threat to privacy of data. The privacypreserving data mining is extensively used to maintain the privacy of the underlying data. Privacy-preserving data mining (PPDM) algorithms are so constructed that the confidential data which is mined is not revealed to the user running the algorithm. The main concerns of

PPDM is that sensitive raw data like names, addresses are modified from the original database, so that the users of the data will not be able to compromise another person’s privacy. And also, sensitive knowledge obtained from mining which can compromise data privacy must be excluded. Thus, privacy preservation is to be integrated at two levels, users’ personal information and information relating to their collective activity. The former is known as individual privacy preservation and the latter as collective privacy preservation [1].

Privacy preserving of data must safeguard from divulging sensitive data during publication of individual data. To maintain privacy, a number of techniques have been proposed for modifying or transforming the data. To avoid data misuse, the data is anonymized. Many data mining techniques are modified to ensure privacy. The techniques for PPDM are based on cryptography, data mining and information hiding [2]. In general, statistics-based and the crypto-based approaches are used to tackling PPDM. In the statistics-based approach, the data owner’s sanitize the data through perturbation or generalization before publishing. Knowledge models such as decision trees are used on the sanitized data. The advantage of statistics-based approach is that it efficiently handles large volume of datasets [3]. In the crypto-based PPDM approach, data owners have to cooperatively implement specially designed data mining algorithms [4]. Though these algorithms achieve verifiable privacy protection and better data mining performance, it suffers from performance and scalability issues [5].

In recent years, privacy preserving data for a single database has been extensively studied [6]. Data anonymization transforms a dataset to uphold privacy using methods such as k-anonymity using generalization or suppression techniques, so that individually identifiable information is masked. K-

Anonymity transforms data to equivalence classes and each class has a set of K- records indistinguishable from each other [7-9]. Problems with this approach were remedied using techniques like l-diversity and t-closeness [10, 11].

The common methodology of k-anonymity used is generalization, where certain values are replaced with less specific but semantically consistent values. Otherwise, some of the values are suppressed. The problem of discovering optimal k-anonymous datasets using generalization or suppression has been proved to be NP-hard [12, 13]. Minimum data loss can be achieved by optimizing an aggregated value over all features and records. The Evolutionary Algorithms (EA) based on swarm intelligence used simple entities with limited memory evolving into increasingly better solutions. The efficient swarm-based data mining approaches usually are some kind of hybrid approach; such as combining a swarm intelligence technique with some orthodox optimization technique, such as the PSO-based clustering technique where the solution is obtained by k-means clustering [14] or combine several swarm-based approaches, such as the PSO/ACO technique [15].

Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) are population based heuristic search technique, popularly used to solve the optimization problems modelled on the basis of EA. In standard PSO, a particle which can stagnate due to the non-oscillatory route and also suboptimal solutions are obtained due to premature converging. Minimizing or maximizing an objective function based on the constraints imposed is the basic problem faced during optimization. Global optimization is absolutely the best set of admissible conditions achievable for an objective under given constraints. Hybrid algorithms incorporating GA are proposed to overcome the limitations of PSO. These hybrid algorithms have the advantages of PSO with those of GA.

The difference between PSO and GA is the capability to control convergence. In GA, the crossover and mutation rates affect the convergence, but are not comparable to the level of control accomplished through controlling of the inertia weight in PSO. The swarm’s convergence increases radically with the decrease in inertia weight. The drawback being that the PSO converges [16] to stable point, which is not essentially maximum. To prevent the occurrence, position update of the global best particles is changed. The hybrid mechanism of GA updates the genetic operator’s crossover and mutation helps in enhancing the PSO. The crossover operation swaps information between two particles, thus enhancing the ability to fly through new search area [17]. While mutation increases the diversity of the population, and helps avoid the local maxima.

In this work, it is proposed to implement a Hybrid Evolutionary Algorithm using Genetic Algorithm (GA)

and Particle Swarm Optimization (PSO). Both GA and PSO in the proposed system work with the same population. In the proposed framework, k-anonymity is accomplished by generalization of the original dataset and the hybrid optimization is used to search for optimal generalized feature set. The paper is organized as follows: Section 2 reviews some related works in the literature, section 3 details the methods, section 4 gives the results and discussions and section 5 concludes the paper.

• II.    Related Works

Bayardo, et al., [18] proposed an optimization algorithm for k-anonymization. The proposed method searches the space of possible anonymization and forms strategies to reduce computation. The census data was used for evaluation and experiments show that the proposed method achieves optimal k-anonymizations using a wide range of k. The effects of different coding approaches and quality of anonymization and performance were also investigated. Real census data experiments demonstrated that the proposed algorithm could locate optimal k-anonymizations under two representative cost measures and a wide range of k.

Sakuma et al [19] proposed a protocol for a local search and a genetic algorithm for the distributed traveling salesman problem (TSP). In the distributed TSP, the cost function information is possessed by distributed parties and is not disclosed to each other. The proposed method is a combination of genetic algorithms and a cryptographic technique, called the secure multiparty computation, which solves the distributed TSP. The privacy preserving LS that adopts 2-opt as neighbourhood and a privacy preserving GA that adopts EAX as crossover and CCM as selection method based on a protocol that solves private scalar product comparison.

Dehkordi et al [20] introduced a new multi-objective method for hiding sensitive association rules using GAs. The objective of the proposed method is to fully support the security of database and to keep the utility and certainty of mined rules at the highest level. In the proposed framework, a pre-sanitization process called Dataset Pre-Sanitization Process (DPSP) is implemented which selects transaction(s) and item(s) in each transaction to be changed for concealing the association rules. Four sanitization strategies were proposed with different criterion.

Matatov et al [21] proposed an approach, data mining privacy by decomposition (DMPD), for achieving k-anonymity by partitioning the original dataset into several projections with each one of them maintaining k-anonymity. Rejoining the projections resulted in a table which still maintained the k-anonymity. Each projection is used to train a classifier and consequently, a new instance is classified by combining the classifications of all classifiers. Guided by classification accuracy and k-anonymity constraints, the proposed algorithm uses a genetic algorithm to search for optimal feature set partitioning. DMPD was evaluated using ten separate datasets and its classification performance was compared with other k-anonymity-based methods. The proposed DMPD performs better than existing k-anonymity-based algorithms.

• III.    Methodology3.1    Adult Dataset

  UCI Machine Learning Repository provides the ‘Adult’ dataset used for evaluation. It contains 48,842 instances, including categorical and integer attributes from 1994 Census information. It has about 32,000 rows with 4 numerical columns, the column which includes age {17 – 90}, fnlwgt {10000 – 1500000}, hrsweek {1 – 100} and edunum {1 – 16}. The age column and native country are anonymized using k-anonymization. Table 1 shows the original attributes of the Adult dataset.

• 3.2    K-Anonymity

• 3.3    Genetic Algorithm (GA)

Table 1: Attributes of the Adult Dataset

Age	native-country	Class
39	United-States	<=50K
50	United-States	<=50K
38	United-States	<=50K
53	United-States	<=50K
28	Cuba	<=50K
37	United-States	<=50K
49	Jamaica	<=50K
52	United-States	>50K
31	United-States	>50K
42	United-States	>50K

In Genetic Algorithm (GA), a group of individuals called chromosomes forms the population that represents a complete solution to a defined problem [25, 26]. Each chromosome is encoded using a sequence of 0s or 1s. The GA begins using a randomly generated set of individuals as population. In each iteration, a new population is generated which replaces all of members of the population. Though, certain number of the best individuals is kept from each generation and is copied with the new generation (this approach known as elitism). The best chromosome in the population is used to generate the next population. Based on the fitness functions, the population will transform into the future generation.

On evaluation of population’s fitness, fittest chromosomes are selected for reproduction. Lower fitness chromosomes or poor chromosomes might be selected in very less numbers or not at all. There are popular selection methods such as "Roulette-Wheel" selection, "Rank" selection and "Tournament" selection. In this study, Tournament selection is used wherein two chromosomes are chosen randomly from the population. First, for a predefined probability p, the more fit of these two is selected and with the probability (1-p) the other chromosome with less fitness is selected [26].

The crossover operation in GA combines two chromosomes together to produce new offspring (child). Crossover occurs only with crossover probability. Chromosomes remain the same when not subjected to crossover. The idea behind crossover is considering new solutions and exploiting of the old solutions. As fittest chromosomes are selected more, good solutions are carried to the next generation. In this study, singlepoint crossover has been applied to produce new offspring for that a high value of crossover probability is used (between 0.80 and 0.90).

Due to crossover operation, the new generation will contain only the character of the parents. This can lead to a problem saturation of finding a better population as no new genetic material is introduced in the offspring. Mutation operator introduces new genetic patterns into the new chromosomes. The new sequence of genes due to mutation may or may not produce desirable features in the new chromosome. The new mutated chromosome is kept if the fitness is better than the general population.

• 3.4    The Particle Swarm Optimization (PSO)

The Particle Swarm Optimization (PSO) algorithm is an adaptive algorithm made of population of individuals (commonly referred to as particles), adapting through returning stochastically toward previous successful regions [27, 28]. The two primary operators in PSO are Velocity update and Position update. During iteration, particle is accelerated toward the particles in the previous best position and the global best position. A new velocity value is updated for each particle at iterations and the updated velocity is based on its current velocity, distance from its previous best position, and distance from its global best position. This is utilized to calculate the next position of the particle in search space. The procedure stops either on iteration of a specific number of times, or till a minimum error is obtained [29, 30].

PSO begins with a group of random particles or solutions and searches for optima through updating of generations. The two "best" values, pbest and gbest , of the particle are updated in each iteration. ‘ pbest ’ is the best solution (fitness) achieved till then and ‘ gbest ’ value is the best value obtained till then by any particle in the population. PSO is computationally simple as it requires only primitive mathematical operators. Particle positions and velocities are assigned randomly in the beginning of the algorithm. PSO updates all velocities and positions of all the particles iteratively as follows:

v d = wv d + c i r i ( p d ^- x d ) + c 2 r 2 ( p d ^- x d ) x d = x d + v d

where

d i - new velocity of the ith particle computed based on the particle’s previous velocity, distance between the previous best position and current position and distance between the best particle of the swarm d - number of dimensions, i - size of the population, w - inertia weight, r1 and r2 are random values in the range [0, 1]

c1, c2 are positive constants, xd i - the new position of the particle.

In classical PSO, the particles tend to get trapped in the local optimum in the gbest region if gbest is far away from the global optimum. To overcome this, the particles are made to fly through a larger search space and pbest position of a particle is updated based on the pbest position of all the particles in the swarm. This improves the diversity of the swarm and local optimum is avoided. The updating velocity of the particle is given by:

Vd = w* vd + c * randd * pbestd  - xd i                    i                          i                      fi (d)        i

f =[f (1),f (2),...,f (d)]

Where i     i      i          i       refers to the pbest pbest that the particle i used and       f( ) is the dimension of particles pbest. Two particles are selected randomly and one of it whose velocity is updated is left out. To update the velocity, the fitness value of the individual particles pbest is compared to select the best dimension.

• 3.5    Hybrid GA-PSO

Cooperative search is a type of parallel algorithms, where several search algorithms are run in parallel to solve the optimization problem. As the search algorithms may be different, cooperative search technique is viewed as a hybrid algorithm [31]. In this work, it is proposed to implement a Hybrid Evolutionary Algorithm using Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). Both GA and PSO in the proposed system work with the same population. Initially, Ps individuals which form the population are generated randomly. They can be considered chromosomes in GA, or as particles in PSO. After initialization, new next generation individuals are created by enhancement, crossover, and mutation operations. The architecture of the proposed hybrid algorithm is given below.

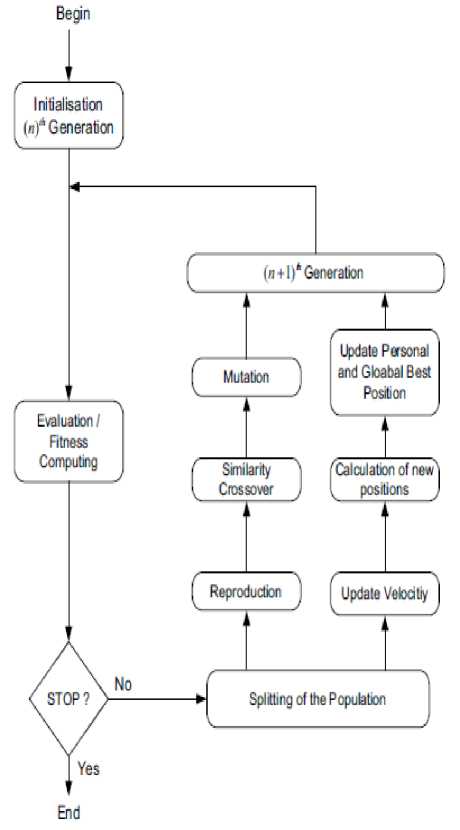
Fig. 1: Flowchart of the Proposed Hybrid Algorithm incorporating GA and PSO

• IV.    Results and Discussion

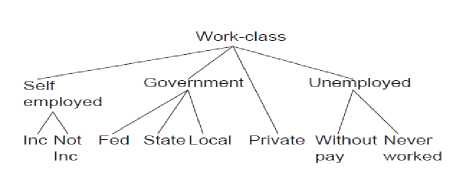
The generalization depends on the type of data; it can either be categorical or numeric. The generalization of the categorical data (gender, work, zip code) is described by a taxonomy tree as seen in Figure 2. The Figure shows an example for generalization of continuous data used in this work.

• Fig. 2:    Example for Generalization of continuous data as a taxonomy tree

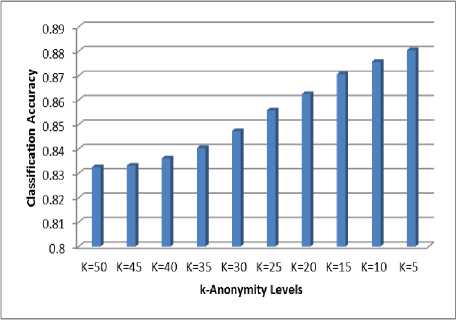
Table 3: Classification Accuracy for different levels of k-anonymity

k-anonymity level	Classification accuracy
K=50	0.832500717
K=45	0.833135416
K=40	0.836083698
K=35	0.840362803
K=30	0.847242128
K=25	0.855759387
K=20	0.862454445
K=15	0.870582695
K=10	0.875619344
K=5	0.880389828

For generalization of numeric data (age, income) is obtained by discretization of its values into a set of disjoint intervals. Various levels of discretization defined, for numeric data of age, the set of intervals:

{(0,10),(10,20),(20,30),..};

{(0,20),(20,40),(40,60),..};

{(0,30),(30,60),(60,90),..} are valid.

Experiments are conducted for different levels of k-anonymity (5, 10, .., 45, 50). Hybrid algorithm is used to find the optimal generalization feature set. Table 2 shows the parameter used for GA in this study. Following Figures and Tables give the results of classification, precision and recall for class label income. The precision and recall is shown for value greater than 50K and less than or equal to 50K.

Table 2: The Proposed Hybrid Algorithm Parameters

Initial population size	25
Maximum generations	20
Number of epochs	500
Momentum optimization	Lower bound 0.5 Upper bound 1.0
Step size optimization	Lower bound 0.1 Upper bound 0.5
Encoder mechanism	Roulette
Cross over	Single point
Cross over probability	0.9
Mutation	Uniform
Mutation probability	0.01

• Fig. 3:    Classification Accuracy for different levels of k-anonymity

It is observed from Figure 3, that the classification accuracy decreases with the increase in k-anonymity level. Figure 4 and 5 show the precision and recall for class label income greater than 50k and less than or equal to 50k respectively.

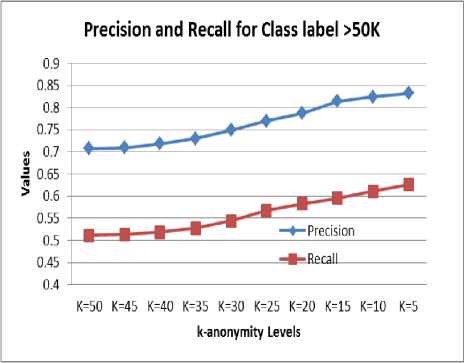
Fig. 4: Precision and Recall for different levels of k-anonymity for class label >50K

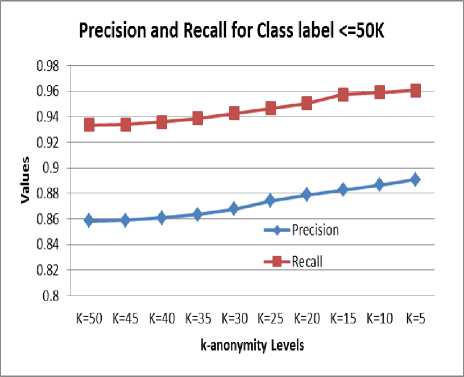
Fig. 5: Precision and Recall for different levels of k-anonymity for class label <=50K

• V. Conclusion

Existing Evolutionary Algorithm (EA) solutions in privacy-preserving domain mainly deals with specific problems such as cost function evaluation. In this work, it is proposed to implement a Hybrid EA using Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). Both GA and PSO complement each other to provide global optimization. In the proposed framework, k-anonymity is accomplished by generalization of the original dataset. The hybrid optimization is used to search for optimal generalized feature set. Experiments were conducted for different levels of k-anonymity and the results obtained are satisfactory.

Acknowledgments

We profusely thank our most generous management for allowing us to make use of the infrastructure on the campus and the support extended for the fulfilment of the research paper. The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.