A hybrid approach for requirements prioritization using LFPP and ANN

Published Online January 2019 in MECS

Requirements prioritization is necessary for any organization, and process to solve the issue of disparity, disagreement and collision [1, 2, 3]. For prioritizing the requirements as per their importance industrial organization are finding new strategies and improved solutions to accomplish the concerns of stakeholder over conflicting requirements [4].To overcome the issues of stakeholders, requirement engineering provides techniques to resolve vagueness fuzziness and ambiguities subject to the clashing and conflicting concerns. A requirement prioritization technique utilizing relationship network mulls over various points of view of partners that use the idea of connection to process weighted needs of requirements [1]. Reproduction strategy organizes the necessities of blended techniques utilizing spry and design based approach [5]. Prioritization utilizing Cost and advantage technique sets up the significance of cost and advantage relating to each necessity [6]. Analytical Hierarchy Process(AHP) is a numerous MCDM(multi-criteria decision-making) procedure that make use of a couple astute examination grid to register the relative estimation of requirements about each other [7].Cluster based mechanized technique communicates different worries of partners to various classes of prerequisites, for example, include based, nonutilitarian and other bunch prerequisites [8].Increments and varieties of client requests, advances of late advances in correspondence and data frameworks, rivalry in worldwide condition, diminishes in administrative directions and increments in ecological cognizance have constrained organizations for concentrating on SCM (supply chain management) [9].

The SCM described the mix of exercises to obtain materials, convert them into moderate merchandise, last items and suggests to clients. The store network comprises of all connections from providers to clients of an item [10].It has expressed that SCM is most important issue of SCM on the grounds that the price of unfinished material and segment parts forms the principle price of an object and the majority of the organizations require to spend impressive measure of their business incomes on buying. In lots of enterprises the price of unfinished materials and segment parts forms the fundamental price of an object, with the end goal that at times it can show up to 70.00% [11]. In big innovation companies acquired objects, materials and administrations speak to up to 80.00 % of aggregate item price [12]. In this way the buying division can assume a key part in an association's productivity and adequacy since the office directly affects cost decrease, benefit and adaptability of an organization by choosing the correct providers essentially lessens buying costs and enhances corporate aggressiveness [13].

Supplier selection (SS) is a requirements prioritization issue based on MCDM which integrates both quantitative and subjective elements [14, 15]. Keeping the goal in mind to choose the best supplier, it is important to build an exchange among these unmistakable and impalpable aspects some of which may strife [15].The goal of SS is to distinguish washing machine suppliers with the most astonishing probable for addressing an organization’s requires reliably and at on admirable cost. Determination based on multiple criteria is a wide examination of suppliers utilizing a typical arrangement of measures and criteria. Be that as it may, the stage of detail utilized for looking at prospective suppliers may change contingent upon a company's requirements. Although AHP is generally favoured for taking care of requirements prioritization based on MCDM issues in actual conditions, this is lacking to clarify unverifiable states in particularly combined shrewd co-relation organizes[16]. The greater part of person’s decisions are not in written to as accurate information. Because a part of the assessment criteria are quantitative and subjective in natural world [17]. It is exceptionally hard for the leader to state the inclinations utilizing careful numerical esteems and to offer correct combination insightful correlation decisions [18]. Fluffy assessments for requirements prioritization in MCDM process are extremely valuable to handle these cons of AHP. Existing requirements prioritization techniques for ‘supplier selection problem’ suffers from a number of limitations like negative degree of membership functions having no sense, non uniqueness outcomes ,scalability problem, time complexity etc. So in this research paper we proposed a hybrid approach for requirements prioritization using logarithmic fuzzy preference programming (LFPP) and artificial neural network (ANN) to overcome these limitations. A case study also adopted from Ozcan et al. [1] to select the superlative supplier organization providing the maximum customer satisfaction amongst all technical features. The technical investigation was conducted on MATLAB software and outcome examined on fuzzy comparison matrix with three supplier selection criteria based on LOGANFIS and FAHP that represents the multi-criteria decision making(MCDM)    outcomes    for    requirements prioritization is superior than existing techniques having higher priority.

• II.    Related Work

  Gülçin Büyüközkan (2017) has combined the first time the Interval Valued Intuitionistic Fuzzy (IVIF) Analytic Hierarchy Process (AHP) to evaluate the multiple criteria weights for requirements prioritization and IVIF Additive Ratio Assessment (ARAS) methodology for alternative assessment procedure. This method also analyzes the selection of a best supplier in an authentic case study from Turkey to exhibit the validity of this approach. [19] Nguyen et al. (2016) has presented an integrated MCDM framework consisting of FAHP (Fuzzy AHP) and fuzzy ARAS methods for evaluating and selecting conveyors. The proposed method has its distinctive merits by combining IVIF AHP and IVIF ARAS for the first time [20].Prof. Aarti M. Karande (2016) has presented distinctive strategies in light of fuzzy decision techniques are thought about for methodology advancement. Each administration gave by association is mapped with SCM procedures. From this arrangement of administrations, ideal administration is chosen. This paper clarifies a contextual analysis of an association dealing with SCM procedures. This paper can't discover readiness list for administrations in light of the value-based process [21].

Swati Dhingra (2016) has established FIS (fuzzy interface system) for prediction of requirements prioritization method based on certain rules. One drawback of this proposed Fuzzy model is it gives inaccurate results on the boundary values of input data set. It validated the outcomes by using J-48 decision tree approach [22].

Kanza Gulzar (2017) has introduced a novel system that spotlights on the mapping of ease of use requirements attributes to the linguistic evaluation from the clients utilizing fuzzy logic (FL). This system organizes clashing ease of use prerequisites properties. For execution, we have utilized MATLAB Fuzzy Logic Tool box. This proposed system is gone for helping the prerequisite expert in taking better choices via robotizing the entire procedure of distinguishing and settling ease of use necessities clashes. The significant undertaking in the proposed framework includes deciding the numerical incentive for each characteristic considering their individual significance in various quantitative and subjective assessment principles. On the premise of numerical value, clashes and their separate severities are recognized [23]. Laurent, Paula (2007) and Davood Golmohammadi (2011) and have displayed a fuzzy multicriteria decision-making (MCDM) is introduced in light of encourage forward ANN. This model is utilized to catch and speak to the chiefs' inclinations. The topology of the NN display is created to prepare the model. This model can utilize chronicled information and refresh the database data for options after some time for future choices [24, 25]. Malakooti (1994) developed the reproduction of the supervisors' choices is shown in detail and the plan and execution of the model are represented by a contextual analysis [26].

• III.    Limitations of Existing Prioritization Techniques

• i.     Don’t maintain the scalability with vast

numbers of requirements.

• ii.     The difficulty of time complexity.

• iii.     The majority of the prioritization techniques

does not compute accurate consistency Ratio (CR= Consistency Index (CI)/Random Index(C).

• iv.    No meaning if negative degree of membership

function occurs.

• v.     Majority of the prioritization techniques

produce multiple optimal outcomes makes strong inconsistency between fuzzy decisions.

To overwhelm of these limitations/drawbacks with existing prioritization techniques we proposed an effective model which named as “A Hybrid Approach for Requirements Prioritization Using LFPP and ANN".

• IV. Proposed Methodology

The proposed requirements prioritization model as shown in fig. 1 is developed to prioritize the requirements as per their priority of order in MCDM for SS(Supplier Selection) is fully based on three criteria (i.e. Service performance criteria, Supplier criteria and product performance criteria) [1].

As found in the fig. 1, to start with, the experts collaborating with the database determine fitting hardware and assembling gear and save them in the database. After that, judges take their criteria for choosing apparatus and assembling hardware. The multiple criteria as a part of information are entered. In the information entry stage, the information are examined and sorted out as a LFPP and ANN outline. The data go into a pre-assembled MATLAB programming as fuzzy pair-wise investigations frameworks. In extension, the prepared NN analyzes the propriety or impropriety of decision maker’s (DM). Truth be told, this component exhibits the intellectual MCDSS (multi-criteria decision support system). In the event that the outcomes are suitable, the choices are affirmed; generally, the passage information ought to be reconsidered and will be come back to the cycle.

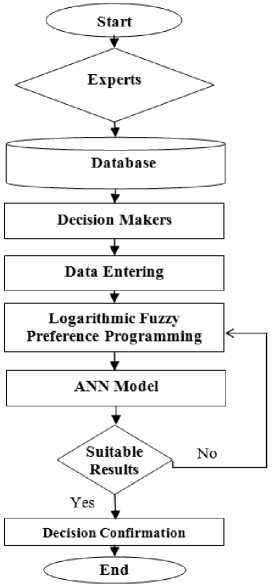
Fig.1. Flow Chart of Proposed Model

• A.    Expert Model

It can be chosen from the supervisors and experts of the plant or from counseling firms.

• B.    Database Model

Database incorporates the determinations of assembling hardware and gear and furthermore productive assembling frameworks that are made out of the data gave by experts.

• C.    Decision Makers Model

Washing machine selection process is done through DM. In a piece of writing permitted "The way toward choosing new machine appliances of a company” it was found that the experts and designers required by 6 % during the time spent choosing gear and the rest of the have a place with the senior chiefs. As you most likely are aware, these are the specialists and workshop chiefs who know about the points of interest of the hardware, not the supervisors. In this manner, they should be consistently required to choose the choice of gear. In this paper, we have attempted to utilize their remarks to outline the LFPP framework.

• D.    Data Entering Model

• a.    LFPP Model

Proposed objective to solve the above problem inextent analysis are:-

• 1.    Provide positive degree (β) of membership function (i.e. between 0 & 1) to make strong

• 2.    Providing a normalized most favorable unique priority vector for every fuzzy judgment to eliminate the inconsistency.

• 3.    The priority vectors generated using lower or upper triangular components of ‘fuzzy pair-wise comparison matrix’ are identical

consistency among the fuzzy decision making.

Assume DM gives fuzzy choices rather than exact choices for a pair-wise comparison framework, at that point it might be chosen the criterion i is amongst aij and cij times as vital as standard j through bij being the no doubt times. At that point, a fuzzy TFN (Triangular Fuzzy Number) pair-wise comparison framework can be spoken to as [1].

(1,1,1)

J = I (^2i, b2i, C2i)

(1,1,1)

(tt13> b13, ^13)..... (^1n, b1n, ^1n)

(tt23,b23'^23)...... (^2n, b2n, ^2n)

(^rn, b^i, cni)   (d„2, b„2, сП2) (апз, ьпз, с„з)..... (1,1,1)

I

For the fuzzy pair-wise comparison matrix in equation

(1 ), we get its logarithmic by using the following equation:

Namely, the logarithmic for a triangular fuzzy decision a ,, whose degree of membership function could be consequently expressed as:

lna_t j = (lna ij, lnb ij , Inc ij, )       i ,j= 1,.n.    (2)

Г    1п^,)-1-»,) , 4‘"®)=- ln(bij)-ln(aij)   '           W      ij' ZnCD =0,        bij 6„ l       1’(с«|)-1’(Ь«|)   '           \Ej/ - lj' degree of

Where ц^ (ln (E) ) is a membership ln (Ei) corresponding to the fairly accurate triangular fuzzy decision lnai7- = (lnaij, lnbij, lncij)- This is extremely common that we suppose to get a crisp priority weight vector to maximize the minimum degree of membership function is given below in equation (3)

^e = minf^ ij

(m( E j ))

|i = 1......n —

1; j = i + 1......n}

Finally this resulting methodology can be created as:

Maximize β

Subject to ( ^ij (ln j - e,i 1.....n 1;j i + 1

( E i - 0,i = 1,..,n.

Maximize 1–β(6)

( —lnE i + E j + ein(b ij /a ij ) - In(a ij ) , i = 1,..., n — 1; j = i + 1,..., n

Subject to { infi — Ej + ein(cij/bij) - -ln(cij), i = 1,..., n — 1; j = i + 1,..., n

I E i - 0,i = 1,. ..,n.

It is seen that the standardization (normalization) limitation Xn=i Ei = 1, is not fused in the over two conditions. This is a result of the way that the conditions will turn out to be computationally troublesome if the standardization imperative is contained. Indeed, standardization can be done after the needs are taking from condition (7). Before standardization, without loss of generality, one can assume that Ei - 1 for all i = 1,. . . ,n with the end goal that lnEi - 0 for i = 1,. . . ,n. Kindly note that the non-negative supposition for ln Ei - 0, i=(1.....,n) isn't vital. We think about this supposition to have ease in an arrangement. Ordinarily, there is no certification that condition (7) will dependably give a positive numerical value for the membership degree β. One of the primary purposes for creating a negative numerical value for β is that there are no priority weights that can satisfy all the fuzzy decisions inside their support interval. This implies, not every one of the inequalities lnEi - lnEj - ein(bij/aij) - lnaij or -lnEi + lnwj - в1п (cij/ bij) - - lncij can be held in the meantime. To maintain a strategic distance from β from catching a negative value, we set up nonnegative decision factors ∂in and ῂij for i= 1,. . . ,n-1 and j = i + 1,. . . ,n with the end goal that they collect the accompanying disparities:

InE i — InE j — In(b ij /a ij ) + 5 ij - Ina ij ,i = 1,....,n — ,, 1; j = i + 1,.... n                      (8)

—InE i + InE j — In(c ij /b ij ) + Пц - —InC ij , i = 1,...., n — 1; j = i + 1,.... n                      (9)

This is the very fortunate that the estimations of the deviation factors are the littler and the superior. Hence we proposed the accompanying LFPP-based nonlinear priority method for FAHP weight deduction:

к = (1 — в) ² + M. V .'   Z y=i ₊ i (S ²ij + _?;'J     (10)

Zj - Zj - pin (bj) + 5ij > Inaij, i = 1,..., n - 1; j = i + 1, ..., n,

Subject to

V

-zi + Zj - ein (cj) + nij > -Incij, i = 1,..., n - 1; j = i + 1, ..., n в, zi > 0, i = 1,..., n,

5ij, nij > 0, i = 1,..., n - 1; j = i + 1,.... n,

Where zi = lnEi for i = 1,. . . ,n and M is a predefined satisfactorily vast consistent, for example, M = 103. The principle reason of bringing a major steady M into the above condition is to set up the weights inside the scope of the help interims of fuzzy decisions so that there won't be any infringement in the framework or even little infringement as could be allowed. In this way, the primary need of condition (11) is given to lessen the infringement of the choices and the weights that are utilized to improve to amplify the DM's fulfillment, to be specific, the estimation of β. Hypothetically, L1 or L∞ standard can likewise be utilized as a part of its place of the L2 standard of the capacity of condition (10) to the deviation factors and enrollment degree. Once the condition is straight, we can comprehend these two standards which may in some cases create numerous ideal arrangements. Henceforth they are overlooked.

Let z * (i = 1, . . . ,n) be the optimal or most favorable result to equation (11). For fuzzy pair-wise comparison matrix J = Пу the normalized priorities of requirements can then be obtained as:

c* _ ^exp(z i ⁾ i — 1 n

^E i “^exp^ * ) ' i= ¹n, ⁽¹²⁾

Here exp () is an exponential capacity, to be specific exp(z * ) = e ^Z for i = 1,. . . ,n. We allude to the strategy that uses condition (11) for FAHP need induction as the LFPP philosophy and the resulting needs as the LFPP needs. Regarding LFPP approach, we have the accompanying explanations

Statement 1: The priority weights of requirements generating by LFPP technique of lower triangular components of a fuzzy pair-wise comparison grid are accurately same as those consequent generating from the upper triangular components of the fuzzy pair-wise comparison matrix [1].

Proof: Let us consider a pair of fuzzy judgments йу = (aij, bij, cij) and aj = (1/cij, 1/bij, 1/aij).The following constraints of equation (11) generated from ajj can be described as:- zj - zi - eIn (T^ij) + ^ij > Inaij, (13)

zi - zj - eIn (j + §ij > -InCjj, (14)

This can be equivalently expressed as

-zi + zj - eIn (cij) + njj > - Incjj,         (15)

zi - zj - eIn (^ij) + nij > Inaij,           (16)

It is extremely easy to seem at these two lack of equalities are accurately the constraints of the equation (11) for^j. These constraints of the equation (11) have a_i j and a j for all time same. As a result, the use of lower/upper triangular components of the fuzzy pair-wise comparison matrix for weight examination for all time provides equal priorities when LFTA technique is applied.

Statement 2: The LFPP strategy generates unique most favorable or optimal priority vector for requirements prioritization in normalized form for any fuzzy pair-wise comparison grid [1].

Proof: The capacity of the condition (11) is a convex function as its Hessian lattice is unquestionably positive. The requirements of condition (30) are for the most part linear inequalities which are shaped as a curved feasible region. Consequently, condition (11) is a convex programming. Through improvement hypothesis, this is expressed that for a convex programming through a strict raised target work, the nearby arrangement has one worldwide ideal arrangement. In this way, the ideal answer for condition (11) is one of a kind.

When all is said in done, it is fortunate that a positive ideal value can be accomplished for β. In the event that its ideal value ends up being β*= 0, at that point there exists solid irregularity among the fluffy choices unless §*= E r=i¹ E ;= _i+ i (S ²j + p ²j ) =0.The greater estimation of δ*, the more grounded the irregularity among the fuzzy choices. Along these lines, the estimation of δ*, can be dealt with as an irregularity assessment for fuzzy pairwise comparison lattices.

• b.    Artificial neural network (ANN) model

In common, ANN can be classified into two categories:

• i.    Supervised ANN

There is normally an eyewitness within the supervised ANN who can calculate the result of the system and replicate their execution authenticity NN (neural network).

• ii . Unsupervised ANN

Unsupervised Neural Network (NN) has no eyewitness. At the end of the day, there is no assessment mirroring the execution legitimacy of NN [1]. Supervised training is considerably more adjustable than unsupervised training [27]. Encourage forward back approach is a standout in the middle of the most widely recognized training policies in ANN [28]. As indicated by the many examinations in the writing by the writer, there is no particular legitimate standard to decide the quantity of shrouded layers. Zahari Taha and Sarkawt Rostam have likewise clearly depicted this problem in this research paper [29].The quantity of neurons: in a large portion of assets, the total number of information layer neurons is equivalent to the number of sources of info; the total number of yield layer neurons is equivalent to the total number of yields. The following four relations have been represented to make a decision for the number of hidden layer neurons, yet it isn't expressed which one is the best technique [30, 31, 32]. These four connections include

NHL = (IL x OL)2

NHL = |(IL + OL)

NHL =1 (IL + OL) + (SL)^

NHL = 2(IL)

In these above given four relationships, IL is represented by the total number of input layer neurons, where OL are the total numbers of output layer neurons and SL is the total number of samples.

• E.    Decision Making Model.

Finally, the data of fuzzy learning made through LFPP and ANN is reported to the DM. The decision makers

(DM) settle on an ultimate choice by these two ways, authorization of the decision or revision.

• F.    Application of SS (Supplier Selection) procedure in the white organizations of goods:

In Europe a largest product maker company , founded in Turkey, desires to choose one of the most excellent supplier based on three criteria named as product performance, supplier criteria and service performance criteria shown in Fig. 2 and its essential parts used in the manufacturing of washing machines. The manufacturing company has washing machine, A/C factories and refrigerator, which are demanded for its production of goods in 100 or more countries like in France, Germany, Spain, and England etc. The yearly capability of this manufacturing organization, which came first and won the nickname of “the most creative ability in the field of production on earth” by the quantity of goods for each capita, is 2 million units annually. This manufacturing company of washing machine, making an export in the amount of approximate 230 million USD yearly is predictable. The washing machine organization examined in this investigation is novel in this segment and it is endeavoring to build its client base. So the manufacturing facility and capability of the manufacturing supplier to enhance its power should be considering into account to choose the top supplier industry. Because of white good division, there are seasonal variations.

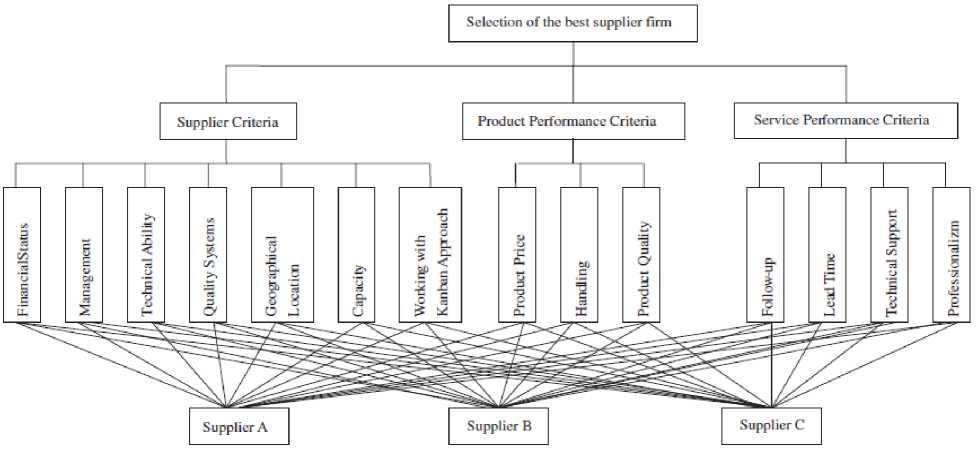
The capability of supplier should be comfortable and enough to meet the modifications as per market requirement. Because the manufacturing process is fully based on assembly and whole raw material of manufacturing are outsourced. The capability of the company is 2.0 million units annually. There is a huge amount of raw or unprocessed manufacturing material supplied. So we can concluded that the SS (supplier selection) is the most significant RP (requirements prioritization) issues in the washing machine company [1].The fuzzy pair-wise evaluation matrix regarding the objective with Triangular Fuzzy numbers (TFN) can be represented in Table 1. The same computations were adapted to one more pair-wise comparison matrices and priority weights of every alternative, key attribute and coattribute were computed. The weights of priority of every main attribute, alternative and sub-attribute can be represented in Table 2. Every column of the comparison matrix in every row. Finally the priority weights of the alternatives regarding supplier attributes were computed.

• V.    Results of Proposed Model Using Matlab for Real Life Example of Supplier Selection [1]

As seen in table 9 and 10, the priority weights of alternatives for requirements prioritization regarding key attributes were merged to evaluate the values of priority weights of substitutes or alternatives for sub elements or attributes of service performance and product performance criteria. In requirement prioritization process, to simplify the procedure of SS problem, priority weights of alternatives are calculated using MATLAB and based on comparison using main elements or attributes, sub- attributes and substitutes or alternatives. A series of questionnaire filled out by experts and evaluate priority weights of the alternative firms using MATLAB. The weights of alternatives are to be (0.45, 0.34, and 0.20). At last, the ‘Supplier A’ in result is most favored supplier having highest weight priority and ‘Supplier B’ is next substitute or alternative supplier as per the defined requirement basis.

Table 1. Fuzzy Estimation Matrix Regarding Goal with TFN (Triangular Fuzzy Numbers)

Criteria	Supplier Criteria	Product Performance	Service Performance	FTA Priorities	LOG-ANFIS
Supplier Criteria	(1,1,1)	(2/3,1,3/2)	(2/3,1,3/2)	0.33	0.3300
Product Performance	(2/3,1,3/2)	(1,1,1)	(3/2,2,5/2)	0.45	0.4299
Service Performance	(2/3,1,3/2)	(2/5,1/2,3/2)	(1,1,1)	0.22	0.2501
β= 0.7

Table 2. Fuzzy Pair-wise Comparison Matrix for Three Substitutes or Alternatives Regarding the Sub-Criteria of Supplier

	Supplier A	Supplier B	Supplier C	FAHP	LOG-ANFIS
A: Comparisons of three substitutes regarding the sub-criterion Financial Status (FS)
Supplier A	(1,1,1)	(1/5,1/3,2/5)	(2/9,1/4,2/7)	0.1	0.2831
Supplier B	(5/2,3,5)	(1,1,1)	(3/2,2,5/2)	0.84	0.5558
Supplier C	(7/2,4,9/2)	(2/3,1/2,2/3)	(1,1,1)	0	0.1611
р= 0.833
B: Comparisons of the three substitutes or alternatives regarding the sub-criterion Management (M)
Supplier A	(1,1,1)	(2/5,1/2,3/2)	(2/7,1/3,1/2)	0	0.1831
Supplier B	(2/3,1/2,5/2)	(1,1,1)	(2/5,1/2,2\3)	1	0.6558
Supplier C	(2,3,7/2)	(3/2,2,5/2)	(1,1,1)	0	0.1611
Р =1.0
C: Comparisons of three substitutes or alternatives regarding the sub-criterion Technical Ability (TA)
Supplier A	(1,1,1)	(2/3,1,5/2)	(2/3,1,2)	0.58	0.5681
Supplier B	(2/5,1,3/2)	(1,1,1)	(2/3,1,2)	0.42	0.4598
Supplier C	(1/2,1,3/2)	(1/2,1,3/2)	(1,1,1)	0	0.0279
р =0.359
D: Comparisons of three substitutes or alternatives regarding the sub-criterion Quality System (QS)
Supplier A	(1,1,1)	(2/9,1/4,1/2)	(2/7,1/3,1/2)	0.58	0.5412
Supplier B	(2,7/2,4,9/2)	(1,1,1)	(2/3,1,5/2)	0.42	0.3200
Supplier C	(2,3,7/2)	(5/2,1,3/2)	(1,1,1)	0	0.1388
р= 0.612
E: Comparisons of three substitutes or alternatives regarding the sub-criterion Geographical Location (GL)
Supplier A	(1,1,1)	(2/5,1/2,3/2)	(2/7,1/3,1/2)	0	0.1632
Supplier B	(2/3,1/2,5/2)	(1,1,1)	(2/5,1/2,2\3)	0	0.2000
Supplier C	(2,3,7/2)	(3/2,2,5/2)	(1,1,1)	1	0.6368
р= 0.342
F: Comparisons of three substitutes or alternatives regarding the sub-criterion Capacity (C)
Supplier A	(1,1,1)	(2/3,1,5/2)	(2/3,1,2)	0.58	0.5412
Supplier B	(2/5,1,3/2)	(1,1,1)	(2/3,1,2)	0.42	0.3200
Supplier C	(1/2,1,3/2)	(1/2,1,3/2)	(1,1,1)	0	0.1388
р= 0.359
G: Comparisons of the three substitutes or alternatives regarding the sub-criterion Working with Kanban Approach (WWKA)
Supplier A	(1,1,1)	(2/9,1/4,1/2)	(2/7,1/3,1/2)	0.33	0.3266
Supplier B	(2,4,9/2)	(1,1,1)	(2/3,1,5/2)	0.22	0.2550
Supplier C	(2,3,7/2)	(5/2,1,3/2)	(1,1,1)	0.45	0.4183
р =0.342

Table 3. Fuzzy Pair-wise Comparison Matrix for Three Substitutes or Alternatives Regarding the Sub-Criteria of Product Performance Criteria and Their Alternative

Supplier A          Supplier B            Supplier C             FAHP                 LOG-ANFIS

A: Comparisons of the three substitutes or alternatives regarding the sub-criterion Product Price (PP)

Supplier A Supplier B Supplier C /=1	(1,1,1) (5/2,3,5/2,7/2) (3,7/2,4,9/2)	(2/7,1/5,2/5) (1,1,1) (1/3,2/5,1/2,2/3)	(2/9,1/4,1/3) (3/2,2,5/2,3) (1,1,1)	0.45 0.22 0.33	0.4589 0.2385 0.3026
B: Comparisons of the three substitutes or alternatives regarding the sub-criterion Handling (H)
Supplier A Supplier B Supplier C /=0.45	(1,1,1) (2/3,1,1/2,5/2) (2,3,7/2)	(2/5,1/2,3/2) (1,1,1) (3/2,2,5/2)	(2/7,1/3,1/2) (2/5,1/2,2\3) (1,1,1)	0.58 0.42 0	0.5412 0.3200 0.1388
C:Comparisons of the three substitutes or alternatives regarding the sub-criterion Product Quality (PQ)
Supplier A Supplier B Supplier C 5 =0.123	(1,1,1) (2/5,1,3/2) (1/2,1,3/2)	(2/3,1,5/2) (1,1,1) (1/2,1,3/2)	(2/3,1,2) (2/3,1,2) (1,1,1)	0.45 0.33 0.22	0.4877 0.3123 0.2000

Table 4. Fuzzy Pair-wise Comparison Matrix for Three Substitutes or Alternatives or Regarding the Sub-Criteria of Service Performance Criteria

Supplier A          Supplier B            Supplier C             FAHP                 LOG-ANFIS

A: Comparisons of the three substitutes or alternatives regarding the sub-criterion Follow – Up (F)

Supplier A Supplier B Supplier C /=0.545	(1,1,1) (5/2,5/2,7/2) (3,4,9/2)	(2/7,1/5,2/5) (1,1,1) (1/3,1/2,2/3)	(2/9,1/4,1/3) (3/2,2,3) (1,1,1)	0.45 0.22 0.33	0.4589 0.2385 0.3026
B: Comparisons of the three substitutes or alternatives regarding the sub-criterion Lead Time(LT)
Supplier A	(1,1,1)	(2/5,1/2,3/2)	(2/7,1/3,1/2)	0.45	0.4877
Supplier B	(2/3,1/2,5/2)	(1,1,1)	(2/5,1/2,2\3)	0.33	0.3123
Supplier C	(2,3,7/2)	(3/2,2,5/2)	(1,1,1)	0.22	0.2000
/= 1.00
	C: Comparisons of the three substitutes		or alternatives regarding the sub-criterion Technical Support (TS)
Supplier A	(1,1,1)	(2/3,1,5/2)	(2/3,1,2)	0.58	0.5412
Supplier B	(2/5,1,3/2)	(1,1,1)	(2/3,1,3/2,2)	0.42	0.3200
Supplier C	(1/2,1,3/2)	(1/2,1,3/2)	(1,1,1)	0	0.1388
/= 3090
D: Comparisons of the three substitutes or alternatives regarding the sub-criterion Professionalism (P)
Supplier A	(1,1,1)	(2/9,1/4,1/2)	(2/7,1/3,1/2)	0.58	0.5243
Supplier B	(2,4,9/2)	(1,1,1)	(2/3,1,5/2)	0.42	0.3091
Supplier C	(1/2,3,7/2)	(5/2,1,3/2)	(1,1,1)	0	0.1666
β=0465

Table 5. For Supply Criteria

Criteria	Financial Status (FS)	Management (M)	Technical Ability (TA)	Quality Systems (QS)	Geographical Location (GL)	Capacity (C)	Working with Kanban Approach (WWKA)	Fuzzy Analytical Hierarchy Process (FAHP)	Logarithmic Artificial Neural FIS (LOG-ANFIS )
FS	(1,1,1)	(2/3,1/2,1)	(2/5,1/2,3/2)	(2/3,1/2,1)	(3/2,2,5/2)	(2/3,1/2,1)	(2/3,1/2,1)	0.18	0.1210
M	(1,2,3/2)	(1,1,1)	(5/2,1/2,1/5)	(3/2,2,5/2)	(3/2,2,5/2)	(5,3,2,2/5)	(5,3,2,2/5)	0	0.0466
TA	(2/3,2,5)	(5,3,2,2/5)	(1,1,1)	(3/2,2,5/2)	(5,3,2,2/5)	(2/3,1/2,1)	(2/3,1/2,1)	0.22	0.1820
QS	(2/3,2,5)	(2/3,1/2,1)	(5/2,1/2,1/5)	(1,1,1)	(2/3,1/2,1)	(2/3,1/2,1)	(2/3,1/2,1)	0.31	0.3453
GL	(5,3,2,2/5)	(2/3,1/2,1)	(5/2,1/2,1/5)	(5/2,1/2,1/5)	(1,1,1)	(2/3,1/2,1)	(2/3,1/2,1)	0.04	0.0459
C	(2/3,1/2,1)	(2/3,1/2,1)	(3/2,2,5/2)	(2/3,2,5)	(2/3,1/2,1)	(1,1,1)	(2/3,1/2,1)	0.25	0.2132
WWKA	(2/3,1/2,1)	(2/3,1/2,1)	(3/2,2,5/2)	(3/2,2,5/2)	(5,3,2,2/5)	(2/3,1/2,1)	(1,1,1)	0	0.0459
β=0.508

Table 6. Fuzzy Pair-Wise Comparison for Product Performance Criteria

Criteria	PP	H	PQ	FAHP	LOG-ANFIS
PP	(1,1,1)	(2/3,1,3/2)	(2/3,1,3/2)	0.16	0.3100
H	(2/3,1,3/2)	(1,1,1)	(3/2,2,5/2)	0	0.0650
PQ	(2/3,1,3/2)	(2/5,1/2,3/2)	(1,1,1)	0.84	0.6250
β=0.01

Table 7. Fuzzy Pair-Wise Comparison Matrix for Service Performance Criteria

Criteria	F	LT	TS	P	FAHP	LOG-ANFIS
F	(1,1,1)	(5/2,2,1/2)	(1,1/2,1/4)	(2/3,1/2,1/5)	0	0.1196
LT	(2,1/2,2/5)	(1,1,1)	(2/5,1/2,1/5)	(2/3,1,5/2)	0.23	0.2685
TS	(1,3,4)	(2/5,1,3/2)	(1,1,1)	(2/5,1/2,2)	0.69	0.4500 0.1616
P	(5,2,3/2)	(4,2,4)	(1/2,1/2,5/2)	(1,1,1)	0.08
β=0.4910

Table 8. Sub-Elements or Attributes for Supplier Criteria

	FS	M	TA	QS	GL	C	WWKA	Alterative priority weight
Weight Alternative	0.1210	0.0466	0.1820	0.3456	0.0459	0.2132	0.0459
Supplier (A)	0.2831	0.1831	0.5681	0.5412	0.1632	0.5412	0.3266	0.3723
Supplier (B)	0.5558	0.6558	0.4598	0.3200	0.200	0.3200	0.2550	0.3952
Supplier (C)	0.1611	0.1611	0.0279	0.1388	0.6368	0.1388	0.4183	0.2325

Table 9. Sub Elements or Attributes for Product Performance Criteria

	PP	H	PQ	Alterative or Substitutes priority weight
Weight Alternative	0.310	0.0650	0.6250
Supplier (A)	0.4584	0.4872	0.5412	0.4956
Supplier (B)	0..3200	0.3123	0.3200	0.3177
Supplier (C)	0.1388	0.2005	0.1388	0.1866

Table 10. Sub-Elements or Attributes for Service Performance Criteria

	F	TS	LT	P	Alterative priority weight
Weight Alternative	0.2609	0.2685	0.3891	0.1196
Supplier (A)	0.4584	0.4872	0.5412	0.5253	0.5030
Supplier (B)	0..3200	0.3123	0.3200	0.3091	0.3134
Supplier (C)	0.1388	0.2005	0.1388	0.1666	0.1836

Table 11. Main Elements or Attributes of the AIM

	S	PP	SP	Alterative priority weight LOG-ANFIS
Weight Alternative	0.3300	0.4299	0.2501
Supplier (A)	0.3723	0.4956	0.5030	0.4570
Supplier (B)	0.3952	0.3177	0.3134	0.3421
Supplier (C)	0.2325	0.1866	0.1836	0.2009

• VI.    Conclusion and Future Work

and ease of use and accuracy.