A Hybrid Artificial Bee Colony and Harmony Search Algorithm to Generate Covering Arrays for Pair-wise Testing
Автор: Priti Bansal, Sangeeta Sabharwal, Nitish Mittal
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 8, 2017 года.
Бесплатный доступ
Combinatorial Interaction Testing (CIT) is a cost effective testing technique that aims to detect interaction faults generated as a result of interaction between components or parameters in a software system. CIT requires the generation of effective test sets that cover all possible t-way (t denotes the strength of testing) interactions between parameters. Covering array (CA) and mixed covering array (MCA) are often used to represent test sets. This paper presents a hybrid algorithm that integrates artificial bee colony algorithm (ABC) and harmony search algorithm (HS) to construct CAs for testing all 2-way interactions (pair-wise testing) in software systems. The performance of the proposed hybrid algorithm ABCHS-CAG is compared and analyzed by performing experiments on a set of benchmark problems on pair-wise testing. The results show that ABCHS-CAG generates smaller CAs than its greedy counterparts whereas its performance is comparable to the existing state-of-the-art meta-heuristic algorithms.
Covering array, pair-wise testing, artificial bee colony, harmony search
Короткий адрес: https://sciup.org/15010958
IDR: 15010958
Текст научной статьи A Hybrid Artificial Bee Colony and Harmony Search Algorithm to Generate Covering Arrays for Pair-wise Testing
Published Online August 2017 in MECS
Interaction among parameters in software systems with multiple configurable parameters or among components in component based systems often lead to interaction faults. To uncover these faults, it is important to test all possible interactions between them. Real world software applications generally have large number of configurable parameters and exhaustively testing all possible interactions is impractical due to time and resource constraints. For instance, consider a system having 6 parameters and each parameter has 4 possible values. This will require a total of 46 = 4096 test cases to test the system exhaustively which further increases exponentially with the increase in number of parameters.
However, it has been shown that in a system, majority of the faults are caused due to the interaction of comparatively small number of parameter interactions, usually ranging from 2 to 6. This is the essence of combinatorial interaction testing (CIT) which test the system by generating test cases to cover all t-way interactions (t denotes the strength of testing) between parameters instead of testing all possible interactions [1]. For instance, the number of test cases to test all 2-way and 3-way interactions for the aforementioned system is 19 and 64 respectively which is quite small in comparison to the number of test cases required for exhaustive testing. It is therefore feasible to generate a set of test cases that provides coverage of all t-way interactions instead of all possible interactions. It has also been shown in past by researchers [2, 3] that more than 70% of the failures are generated by 2-way interactions.
For efficient testing it is required to generate a minimal number of test cases that achieve 100% coverage criteria which in our case is the strength (t) of testing. A set of test cases are usually represented by combinatorial structure namely covering array (CA). One of the major problems in the field of CIT is the generation of minimal CA popularly known as CAG (Covering Array Generation) problem [4]. CAG is an NP-complete problem [5]. Many algorithms/tools exist in literature to solve CAG problem. These algorithms/tools falls in three categories: algebraic methods, greedy techniques and meta-heuristic algorithms.
Although greedy algorithms are more popular in the software testing community, meta-heuristic algorithms are more effective as compared to algebraic approaches and greedy algorithms [6]. Moreover, this approach is more flexible as compared to algebraic approaches which require that each component must possess same number of values. The term meta-heuristic describes heuristic methods that can be applied to a wide range of optimization problems [7]. They provide a robust and efficient way to solve complex real world problems. Many meta-heuristic algorithms such as genetic algorithm (GA), artificial bee colony algorithm (ABC), particle swarm optimization (PSO), simulated annealing (SA), and harmony search (HS) have been used successfully by researchers to solve various optimization problems. Recently, an increasing interest of researchers has been observed in hybridizing various meta-heuristic algorithms. The main motivation behind such amalgamation is to obtain an algorithm that combines and exploits the advantages of the individual strategies and covers up the weaknesses of each other.
In this paper we propose a hybrid algorithm ABCHS-CAG (Artificial bee colony harmony search - covering array generation) that combines ABC and HS to solve CAG problem for pair-wise testing of software systems. It is organized as follows. In Section II and Section III, we briefly explain ABC and HS algorithms respectively. Section IV gives a brief overview of combinatorial structures. Section V discusses the existing literature on CAG. Section VI describes the proposed ABCHS-CAG algorithm. Section VII describes the implementation of ABCHS-CAG and presents the result of experiments conducted to evaluate the effectiveness of the proposed approach. Section VIII concludes the paper with a discussion on the future plans.
II. Artificial Bee Colony Algorithm
ABC [8] is a swarm-based algorithm inspired by the intelligent foraging behavior of honey bee swarm. In ABC algorithm, artificial bee colony is divided into three groups: employed bees, onlooker bees and scouts, and the position of each food source represents a possible solution to the given optimization problem. The nectar amount of the food source is the measure of its quality (fitness). In ABC, exploitation is done by means of employed bees and onlooker bees which are equal to the number of food sources (solutions) and exploration is done by scouts. ABC algorithm starts by generating a random initial population of possible solutions to the given optimization problem and each employed bee tries to produce a new solution by updating the selected solution xi using (1).
V j = X '^^ X j + X kj ) (1)
Here, xij denotes the jth dimension of selected solution Xi or (vi), j e{1,2,......., D} is a randomly selected dimension and D is the number of optimization parameters, xkj is a randomly selected neighbor of x where, k e{1,2,......., SN} and SN is the number of food sources in the population. Although k is determined randomly, it has to be different from i. фц is a random number between [-1, 1].
After modification each employed bee applies a greedy selection between the old solution and the newly generated solution and selects the one which has higher fitness (nectar amount of the food source). Once the
search process of employed bees is completed, they share the position and nectar information of the food sources with the onlooker bees. A probability is assigned to each solution xi | 1 ≤ i ≤ SN which is calculated using (2).
P x, ) = SN itnes- xi ) (2)
£ fitnes^ xn ) n = 1
An onlooker bee selects a food source based on the probability assigned to them and performs modification on the selected food source using (1) to generate a candidate food source. A greedy selection is again applied by the onlooker bee as done in case of employed bees. Exploration is done by means of a scout which looks out for solutions which have not been improved by employed bee or onlooker bee through a predefined number of cycles called limit and replaces it with a randomly generated solution. For further explanation of ABC algorithm, readers can refer Karaboga [8].
III. Harmony Search Algorithm
HSA [9] is a meta-heuristic algorithm inspired from the musical performance process that involves searching for a better state of harmony by a musician. In HSA, a musical instrument or note in improvisation corresponds to decision variables in optimization, the range of pitch corresponds to the range of value of the decision variable and a harmony corresponds to a solution vector. HSA starts by randomly generating and storing an initial population of HMS harmony vectors (solution vectors) in the harmony memory (HM), where HMS is the size of HM. During the improvisation process, each musician improvises its notes using one of the three rules 1) by playing a note in his memory, 2) by playing a variation of note in his memory, or 3) by playing a randomly generated note. Whether a new harmony is generated by experience, variation of experience or randomness will depend upon harmony memory consideration rate (HMCR) and pitch adjustment rate (PAR). A new Harmony vector x new = ( x n ew , x n ew , , x new , x n ew ) , where k denotes the number of instruments, is generated by first generating a uniform random number r 1 in the range [0, 1] and if r1 is less than HMCR, the i th decision variable x new is selected by the memory consideration as shown in (3). In the memory consideration, x new is selected from any harmony vector x N in the HM.
Otherwise, x new is selected randomly from all possible values of the respective decision variable (exploration).
new
xi
= <
xiN rand
xi
| r < HMCR | rv > HCMR
Where, N = 1, 2, ......, HMS
In case the decision variable x new is selected from the
HM, a uniform random number r 2 is again generated in the range [0, 1] to determine whether the decision variable (note) generated by memory consideration should be pitch adjusted. If r 2 is less than PAR, then x new is adjusted slightly as shown in (4).
new J XN + Г * BW^ < PAR i [Do not adjust pitch \ r2 > PAR
Where, r 3 is a random number between [0, 1] BW is the distance bandwidth
The above procedure is used to generate all x new | i ϵ {1, 2, …, k}. Finally, HM is updated by replacing the worst harmony by the newly generated harmony if it is better than the former. The above process is repeated until a solution is found or maximum number of generations is reached.
-
IV. Combinatorial Structures
Off late, combinatorial structures have widely been used in software testing for generating test sets. Covering arrays (CAs) are widely used notation to represent test sets. A covering array CA (N; t, k, v) [10] is a N × k array and is used to represent a set of test cases to test all t-way interactions between k parameters (each having v possible values) of the system under test. Each row of a CA corresponds to a test case. One important property of CA is that every t-tuple needs to be covered by at least one of the test case in the CA. An important constraint on CA is that each parameter must have same number of values which is not the case with most of the real world systems. In such cases mixed covering arrays (MCAs) are used.
A mixed covering array MCA (N; t, k, (v 1 v 2 …v k )) [6] is an N × k array and is used to represent a set of test cases to test all t-way interactions between k parameters of the system under test. v 1 , v 2, …, v k indicates the number of possible values of k parameters respectively. MCA can also be represented using the shorthand notation MCA (N; t, k, (w 1 q1 …. w s qs)) which is obtained by combining equal entries in v i | 1 ≤ i ≤ k. Each element w j qi in the set (w 1 q1w 2 q2 ….w s qs) means that q i parameters can take w j values each.
To illustrate an instance of MCA, consider a web application where the user has different choices of browser, operating system (OS), internet protocols, CPU and DBMS as shown in Table 1.
Table 1. Various configuration options
|
Browser |
OS |
Protocol |
CPU |
DBMS |
|
Internet Explorer |
XP |
IPv4 |
Intel |
MySQL |
|
Firefox |
OS X RHL |
IPv6 |
AMD |
Oracle Sybase |
The application must run on any configuration of browser, OS, internet protocol, CPU and DBMS. To check that the application runs on all possible configurations, a total of 2 × 3 × 2 × 2 × 3 = 72 test cases are required. As exhaustive testing becomes infeasible for large number of configurable parameters, combinatorial testing is performed that enables the tester to test the system with relatively less number of test cases. Instances of MCAs generated to test all 2-way and 3-way interactions for the system in Table 1 are shown in Fig. 1(a) and Fig. 1(b) respectively.
|
" IE IE |
OS X XP RHL |
IPv4 IPv6 IPv4 |
Intel Intel AMD |
MySQL"\ Sybase Sybase |
|
|
Firefox |
OS X |
IPv6 |
Intel |
Oracle |
|
|
Firefox |
OS X |
IPv4 |
AMD |
Sybase |
|
|
- 1E. |
RHL |
IPv6 |
AMD |
Oracle |
|
|
Firefox |
RHL |
IPv6 |
Intel |
MySQL |
|
|
Firefox |
XP |
IPv6 |
AMD |
MySQL |
|
|
- 1E |
XP |
IPv4 (a) |
AMD |
Oracle ■ |
9 × 5 |
|
■ Firefox |
OS X |
IPv4 |
AMD |
MySQL |
|
|
1E |
RHL |
IPv4 |
Intel |
Oracle |
|
|
Firefox |
OS X |
IPv6 |
Intel |
Orcale |
|
|
Firefox |
OS X |
IPv6 |
AMD |
Sybase |
|
|
1E |
XP |
IPv6 |
AMD |
MySQL |
|
|
Firefox |
RHL |
IPv4 |
Intel |
Sybase |
|
|
1E |
RHL |
IPv6 |
AMD |
Sybase |
|
|
1E |
OS X |
IPv4 |
AMD |
Oracle |
|
|
Firefox |
XP |
IPv4 |
AMD |
Oracle |
|
|
Firefox |
RHL |
IPv6 |
Intel |
MySQL |
|
|
1E |
OS X |
IPv4 |
Intel |
Sybase |
|
|
1E |
XP |
IPv4 |
AMD |
Sybase |
|
|
1E |
OS X |
IPv6 |
Intel |
MySQL |
|
|
1E |
RHL |
IPv4 |
AMD |
MySQL |
|
|
Firefox |
XP |
IPv4 |
Intel |
MySQL |
|
|
Firefox |
XP |
IPv6 |
Intel |
Sybase |
|
|
Firefox |
RHL |
IPv6 |
AMD |
Oracle |
|
|
- 1E |
XP |
IPv6 (b) |
Intel |
Oracle |
18 × 5 |
Fig.1. Instances of MCA for 2-way and 3-way testing
-
V. Related Work
In the last 20 years, CAG problem has become a popular research area among researchers in the fields of Mathematics as well as Computer Science. Various tools and algorithms have been proposed by researchers to solve CAG problem.
Mathematicians use algebraic methods to generate CAs. These methods are extremely fast; however they are mostly designed to generate CAs only. Greedy algorithms use two approaches to construct CA: test based generation and parameter based generation. In test based generation, CA is constructed by generating one test at a time until all the uncovered combinations are covered. Parameter based generation starts by constructing a small CA for the first t parameters initially and then extends it by taking one more parameter in the next iteration. Extension is done in both horizontal as well as vertical direction.
Recently, meta-heuristic techniques have also been used to solve CAG problem. Meta-heuristic search techniques start from a pre-existing CA or a population of
CA and apply a series of transformations on them until a heuristic algorithms /tools to generate CA for CIT is
CA is found that covers all the uncovered combinations. shown in Table 2.
A summary of various algebraic, greedy and meta-
Table 2. Summary of existing tools/algorithms for combinatorial testing
|
Existing Strategies |
t-way testing |
Category |
Support Constraint |
|
|
Test Cover [11] |
4 |
Algebraic methods (Parameter-based generation) |
v |
|
|
TConfig [12] |
2 |
* |
||
|
Combinatorial Test Services (CTS) [13] |
4 |
v |
||
|
Algebraic Method [14] |
2 |
* |
||
|
AETG [1] |
2 |
Greedy algorithms (Test based generation) |
V |
|
|
TCG (Test Case Generator) [15] |
2 |
V |
||
|
TVG (Test Vector Generator) [16] |
6 |
V |
||
|
AllPairs1 |
2 |
* |
||
|
PICT [17] |
6 |
V |
||
|
Jenny [18] |
≤ 8 |
V |
||
|
Density [19] |
3 |
* |
||
|
CASCADE [20] |
6 |
V |
||
|
ACTS(IPOG) [21] |
6 |
* |
||
|
Paraorder [19] |
3 |
* |
||
|
GA [22] |
3 |
Meta-heuristic Techniques (Test based generation) |
GA |
* |
|
ACA [22] |
3 |
ACO |
* |
|
|
TSA [23] |
6 |
TS |
* |
|
|
SA [24] |
6 |
SA |
* |
|
|
PPSTG [25] |
6 |
PSO |
* |
|
|
CASA [26] |
3 |
SA |
V |
|
|
GAPTS [27] |
2 |
GA |
* |
|
|
PWiseGen [28] |
2 |
GA |
* |
|
|
GA [29] |
2 |
GA |
* |
|
|
CS [30] |
6 |
CS |
* |
|
|
FSAPSO[31] |
4 |
Adaptive PSO |
* |
|
|
TCA [32] |
Two-mode local search |
V |
||
|
PWiseGenPM [33] |
2 |
GA |
* |
|
|
PWiseGen-GM(Greedy Mutation) [34] |
2 |
GA |
* |
|
|
HHSA(Hyper Heuristic Simulated Annealing) [35] |
3 |
SA |
V |
|
|
ABC-CAG (Artificial Bee Colony- Covering Array Generator) [36] |
2 |
ABC |
* |
|
-
VI. The Proposed Hybrid ABC and hs algorithm (Abchs-Cag)
Every stochastic search algorithm is characterized by a trade-off between two mechanisms, namely exploration and exploitation. To find an optimal solution it is essential to maintain a good balance between these two otherwise, the optimization method either suffers from premature convergence to a suboptimal solution or slow convergence. ABC is very good at exploration but poor in exploitation as employed bees and onlooker bees only modify a small part of the solution instead of taking the global best, which may lead to the trapping of ABC in local minima.
In HSA, exploration or diversification is controlled by randomization and pitch adjustment (PA). As discussed in Section III, in HSA randomization generates a new harmony randomly (global search) whereas PA corresponds to the generation of a slightly different harmony (solution). PA is done by adjusting the pitch in the given BW by a small random amount with respect to the existing pitch (solution) from the HM [9]. Although PA is a diversification factor but the subtlety of this is that it acts as an intensification factor because it makes sure that the newly generated solutions are of good quality, at the same time not far from the existing solution.
So PA is a controlled diversification (local search). In HM, exploitation or intensification is represented by HMCR which ensures that good harmonies (solutions) from the HM are transferred to the next generation which as discussed above will further be enhanced by the controlled PA. Therefore, intensification in HSA can be controlled by adjusting the HMCR.
To enhance the exploitation capability of ABC, we present a hybrid algorithm ABCHS-CAG that combines ABC algorithm and HSA to generate CA for pair-wise testing. The main motive behind the hybridization of ABC and HS algorithm is to incorporate the intensification capability of HS in ABC thereby enhancing the performance of ABC algorithm. In ABCHS-CAG, the exploitation ability of employed bees is enhanced by utilizing the memory consideration and pitch adjustment mechanism of HS algorithm. The various steps of ABCHS-CAG are:
Step 1: Generation of initial population
The first step of ABCHS-CAG is the generation of initial population of SN covering arrays CA i = {CA 1 , CA 2 ,…, CA SN } of size N × k. Each CA corresponds to a food source. Initially N is unknown at the start of the search process, so we can use either of the two methods suggested by Stardom [37]. The first one is to set a loose lower bound (LB) and upper bound (UB) on the size of a CA and then apply binary search repeatedly until a solution is found. In case the size of N is known in advance i.e. the best bound achieved in the existing literature, we can start with the known size and try to optimize it further. ABCHS-CAG uses the first method where it starts with a population of large random CAs of size N × k, where N = (LB + UB)/2 and apply binary search repeatedly until an optimal CA is found. In case the size is known in advance, ABCHS-CAG uses the second method. After population initialization, fitness of each CA is calculated which is the measure of its quality. The fitness of CA is calculated by counting the total number of distinct 2-way interactions covered by it as shown in (5):
interactions out of 37 distinct 2-way interactions present in the system. So the fitness of CA 1 is 29. Similarly the fitness of each CA in the initial population is calculated by ABCHS-CAG.
Fitness =
Number of distinct 2 — way) interactions covered by CAi J
V ie {1.. SN}
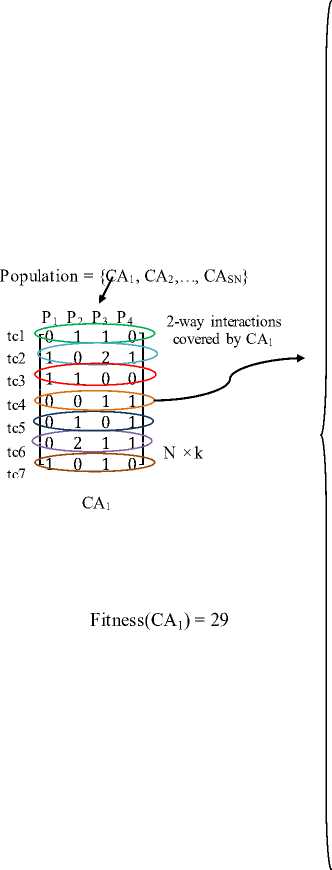
Fig.2. An example to illustrate the way t-way interactions are covered by a CA.
Distinct 2-way
P 1 P 2 interaction


P 2 P 4

An example to illustrate how population of CA is created and how their fitness is calculated is shown in Fig. 2. Here, we have taken a system that has 4 configurable parameters P1, P2, P3 and P4 with P1 and P4 having 2 values and, P2 and P3 having 3 values each. The values taken by each parameter are mapped to set X = {0, 1, 2...}. Let us assume that the CA size N is known in advance and is 7 in our case. To find an optimal CA for testing all 2-way interactions of parameters, ABCHS-CAG starts by generating an initial population of CAs represented by CA i = {CA 1 , CA 2, …, CA SN } of size 7 × 4 and calculates the fitness of each CA. In Fig. 2, all the 2way interactions covered by each test case of the first covering array CA 1 in the initial population are shown. It is clear from Fig. 2, that CA 1 covers 29 distinct 2-way
After generation of initial population of CAs, they are subjected to repeated cycles of the search process of employed bees, onlooker bees and scout bees in an attempt to generate a CA that maximizes the objective function f | f : CA i → I+, where, I+ is a set of positive integer and f (CAi) is calculated as:
f ( CA i ) = fitness ( CA i ) (6)
ABCHS-CAG tries to find a covering array CA max , such that
■ (CA max ) = max(f(CAt )), V i e {1,2.....5N}
Step 2: Initialization of HSA parameters
During this step, the value of HSA parameters i.e., HMCR and PAR is set. The typical value of HMCR varies from 0 to 1. A low value of HMCR will result in selection of only best harmonies from the HM which ultimately results in slower convergence. A high value of HMCR will use most of the harmonies from HM thereby leaving other harmonies unexplored leading to poor solutions. The value of PAR also varies from 0 to 1. A low PAR along with a narrow BW will result in slow convergence whereas; a high PAR along with a wide bandwidth may cause the solution to scatter around some potential optima. Therefore, the values of HMCR and PAR need to be selected carefully.
Step 3: Employed bee phase
Unlike traditional ABC, ABCHS-CAG enhances the exploitation capability of an employed bee by enabling it to select the worst test case of the selected covering array CAi and modify this worst test case represented by CAiq to generate a new test case CAiqnew = (CAiq1new, CA iq2 new, ……, CA iqj new), on the basis of HMCR and PAR. Here, j = 1 to k represents the jth parameter of the worst test case i.e., qth test case of CA i . The worst test case is the one that covers least number of distinct 2-way interactions in the selected CA. The value of each parameter CA iqj in CA iq is modified on the basis of the value of random number r1 which is in the range [0, 1]. If r1 < HMCR, CAiq j new is generated by modifying CAiq j using (8) otherwise, CA iqj new is selected randomly from all possible values of parameter P j .
СА ™" = round fa^ + 0 iqj (CA iqj - CA mqj) )
Where, CA m is a randomly selected neighbor of CA i , Ø iqj is a random number between [-1, 1]
For calculation purpose, the values in the domain of each parameter are mapped to an integer number in the range [0, v j ), where v j is the number of possible values of parameter ‘j’ It is quite possible that a non-integral value may get generated as a result of calculation performed using (8). In such a situation, when a non-integer value is generated for a parameter, it gets rounded to the nearest integer number. After rounding off the value, if it doesn’t fall in the range [0, v j ), then a value is selected randomly from the input domain of the respective parameter and it replaces the existing value of the selected parameter. In case CAiq j new is generated using (8), a random number r2 is generated in the range [0, 1] and the value of PAR is examined. The value of PAR indicates the chances of moving to the left or to the right neighbors of CA iqj new. The movement towards the neighbors as shown in (9) occurs if and only if r2 < PAR. Otherwise, no changes are made to CA iqj new.
cA qew = cA qew ± i (9)
Finally, a greedy selection is applied and CA iq new replaces CA iq , if fitness (CA i new) > fitness (CA i ).
Step 4: Onlooker bee phase
After the employed bees phase, the fitness of each CA in the search space is calculated and a probability of selection is assigned to each of them using (2). An onlooker bee in ABCHS-CAG selects a CA on the basis of probability assigned to them. This is done by generating a random number in the range [0, 1] and selecting a CA based on the interval in which the random number falls. Unlike the traditional ABC, ABCHS-CAG takes advantage of the global best CA denoted by CAbest in the population (based on gbest-guided ABC (GABC) [38])to guide the search of candidate solution and modifies the selected CA. Like employed bee, onlooker bee selects the worst test case (dimension) of the selected CA and replaces it with a test case that is generated by using the information of the global best CA i.e., CAbest and a randomly selected neighboring CA i.e., CAm using (10). The GABC technique drives the new candidate solution CAinew towards the global best solution, thereby improving its exploitation capabilities. However, in case CAbest gets selected per se, based on the generated random number, ABC-CAG modifies it by replacing its worst test case by a smart test case. A smart test case is constructed by selecting the value for each parameter greedily. For each parameter, a value is selected whose occurrence in CAbest is the minimum. The replacement of worst test case in CAbest by a smart test case is done to make sure that certain new pairs get covered by this replacement.
CA^ = CA^ + 0 lqJ (CA^ - CA mqj ) + Vlql (CAb qf - CA lq] )
Here, CAbest is the value of th component of qth test case of CAbbM, Yiqj is a uniform random number in the range [0, C], C is a non-negative constant.
Step 5: Scout bee phase
ABC’s exploration strategy is effectuated by scout bees by replacing a food source abandoned by an employed bee, with a randomly generated food source. To further improve ABC algorithm’s exploration capability, we use a greedy approach to select a CA instead of the primitive approach followed by ABC. In ABC, the food sources that cannot be improved through a predetermined threshold called the limit are abandoned. The aforementioned abandoned food sources are there upon replaced by randomly created new food sources by artificial scout. In ABCHS-CAG, scout replaces the worst CA (least fitness) in the population by a new CA. ABCHS-CAG necessitates setting the frequency of scout operation with discretion: a very high value of frequency will proliferate diversity of the population and avoid getting stuck in local minima but concurrently makes it difficult to converge to a good solution; whereas, a lower value of frequency will result in early convergence leading to sub optimal solution. Hence, it is required to set the frequency of scout denoted by fscoutto an optimal value. ABHSC-CAG replaces the worst CA by a randomly generated CA after every fscout generations.
Step 6: Stopping/Exit Criteria
Step 3- step 5 are repeated until a solution is found i.e., a CA is found that covers 100% 2-way interactions or maximum number of iterations is reached. Now there are two cases:
Input: SUT (t, k, v, N), Output: CA of strength-2
-
1: Set parameters: SN, NI, HMCR, PAR, fscout
-
2: Generate initial population of SN covering arrays CAi | 1 ≤ i ≤ SN
-
3: Calculate fitness of all CAi |1 ≤ i ≤ SN using Equation (5)
-
4: Iteration ← 1, Cycles ← 1
-
5: Employed bee phase // intensification using HS
for i = 1 to SN
Select the worst test case q of CAi for j = 1 to k
Generate a random number r1 in the range [0, 1] if (r1 < HMCR)
СА™ = round(CA iqj + O.U:A , CA mqj) )
Generate a random number r2 in the range [0, 1] if (r2 < PAR) л a new л a new i i CA iq/' = CA iq/ ± 1
end if else
/•Anew_ /• Arandom end if end for if (fitness (CAinew > CAi)
Replace CA , by CA^
end for
-
6: Onlooker bee phase
-
6 .1: Compute the probability of selection of each covering array CAi fitness (CA , )
P(CAi ) = 2 П=1 fitness (CA n )
-
6 2: for i = 1 to SN
let CAi be the CA selected by onlooker bee
← worst test case of CAi
← global best CA if (CA i == CAbest)
replace by smart test case else for j = 1 to k
CA™ = CAlq] + 0iqj (CAiqj - CAmqj- ) + VltB (CA^s - CAlq] ) end for end if end for
-
7: Scout phase
if ( cycles = = fscout)
replace the worst CA i.e.,CA i worst by randomly generated covering array CArandom cycles = 1
else cycles ++ end if
-
8: if ( there exist a CAi that achieves 100% fitness) stop and return CAi
else iteration ← iteration + 1
if (iteration > NI)
return solution not found else goto step 5
end if end if
Fig.3. Pseudo code of ABCHS-CAG
Case 1: If a solution is found at N where, N was determined by setting loose LB and UB on the size of CA i.e., N = (LB + UB)/2 then ABCHS-CAG changes the UB to N-1 otherwise, changes the LB to N + 1 and reexecute with a new initial population of CAs of size N = (LB + UB)/2. This process is repeated until the smallest CA that covers 100% t-way interactions of input parameters is obtained.
Case 2: If a solution is found at N where N was taken from the existing literature, ABCHS-CAG decreases N by 1 otherwise, increases N by 1 and re-execute with a new initial population of CAs of size N × k. This process of incrementing or decrementing N continues until an optimal CA is found that covers 100% t-way interactions of input parameter values. The algorithm ABCHS-CAG is shown in Fig. 3.
-
VII. Evaluation
This section presents the result of experiments performed to evaluate the performance of ABCHS-CAG with respect to the existing algorithms to construct CA for pair-wise testing. We have implemented ABCHS-CAG in Java and three sets of experiments are conducted to make comparison on the basis of CA size and CA generation time. For the first experiment, smart phone application (SPA) benchmark problem [39] is considered. In the second experiment, we have taken a utility in a software application. For the third experiment, some benchmarks problems are carefully selected from the existing literature [6, 24, 25] on pair-wise testing for comparison. CA size is absolute and is independent on the execution environment whereas, CA generation time depends upon the execution environment. Therefore, CA generation time is reported only for publicly available tools.
Experiments were conducted by executing the benchmark problems on these publicly available tools under Windows with INTEL Pentium Dual Core 1.73 GHZ processor and 1 GB memory. As discussed in Section VI, the values of various parameters such as HMCR, PAR, fscout and NI (number of iterations) need to be set before performing the experiments. We performed extensive study with various combinations of HMCR and PAR and reached to a conclusion that HMCR= 0.7 and PAR =0.4 work best in our case. We have set fscout = 5 which means that the scout will replace the worst CA after every fifth iteration which enables us to reach to an optimal solution within reasonable time. We performed experiments with varying number of iterations. NI < 2000 will make the algorithm terminate early for most of the benchmark problems preventing it to converge to a good solution whereas NI > 5000 will not make any significant difference in the quality of final solution. Hence NI is set as 5000. As meta-heuristic techniques/tools generates non-deterministic results, we ran each benchmark problem ABCHS-CAG, ABC-CAG, CASA and PWiseGen-PM 30 times and reported the average and best result obtained in each case. However, we have reported the CA generation time for the best cases only.
-
A. Benchmark 1:Smart phone Application example (SPA)
The wide spread and growing popularity of smart phones have led to the development of tens of thousands of smart phone applications or ‘apps’ annually [39]. Android is one of the platforms for smart phone apps. The behavior of a smart phone can be controlled by setting many configuration options that are available in the android unit, which in turn plays an important role while executing an app on a variety of hardware and software platforms. Table 3 shows the various android configuration options.
To ensure that a particular app works across all possible configurations, a total of 3 × 3 × 4 × 3 × 5 × 4 × 4 × 5 × 4 = 172,800 test cases will be required which is infeasible. Using combinatorial testing, tester can generate a test set to test all t-way interactions between configurations thereby reducing the testing time and effort required by exhaustive testing.
Here, we generate a MCA to test all 2-way interactions between configurations. SPA can easily be represented by an MCA instance MCA (N; t, 9, 334452). The size and the generation time (in seconds) of MCAs generated by the existing state-of-the-art tools/algorithms for 2-way testing of SPA are shown in Table 4.
Table 3. Android configuration options
|
Parameters |
Values |
|
HARDKEYBOARDHIDDEN |
NO, UNDEFINED, YES |
|
KEYBOARDHIDDEN |
NO, UNDEFINED, YES |
|
NAVIGATIONHIDDEN |
NO, UNDEFINED, YES |
|
SCREENLAYOUT_LONG |
MASK, NO, UNDEFINED, YES |
|
ORIENTATION |
LANDSCAPE, PORTRAIT, SQUARE, UNDEFINED |
|
TOUCHSCREEN |
FINGER, NOTOUCH, STYLUS, UNDEFINED |
|
KEYBOARD |
12KEY, NOKEYS, QWERTY, UNDEFINED |
|
NAVIGATION |
DPAD, NONAV, TRACKBALL, UNDEFINED, WHEEL |
|
SCREENLAYOUT_SIZE |
LARGE, MASK, NORMAL, SMALL, UNDEFINED |
Table 4. Comparison of MCA size/MCA generation time (in seconds) for SPA
|
Jenny |
PICT |
Allpairs |
TVG |
ACTS (IPOG) |
CASA |
PWiseGenPM |
ABC-CAG |
ABCHS-CAG |
||||
|
avg |
best |
avg |
best |
avg |
best |
avg |
best |
|||||
|
31/ 0.12 |
30 |
34/ 0.02 |
31/ 0.35 |
29/0.015 |
25 |
25/ 6.57 |
25 |
25 /0.63 |
25 |
25/ 4.03 |
25 |
25/ 3.57 |
-
B. Benchmark 2:MS Word example
Here, we have taken an example of “Insert Table of Figures” feature available in MS-Word that models and illustrates the concept of CIT. It can be seen from Fig. 4 that there are 6 attributes whose values a user can set while using this feature of MS-Word. For example, the user can check or uncheck “show page number” attribute. Similarly, for the “tab leader” attribute a user can select from four possible values which we represent by 0, 1, 2 and 3. Here, each attribute that a user can set is considered as an input parameter and each of them has different possible values. Table 5 summarizes the parameters and the values for “Insert Table of Figures” feature available in MS-Word. It is clear from Table 5 that “Insert Table of Figures” can be represented by an MCA instance MCA (N; t, 6, 234261). Exhaustive testing of this feature will require 2 × 2 × 2 × 4 × 4 × 6 = 768 test cases. The size and the generation time of MCAs generated by the existing state-of-the-art tools/algorithms for 2-way testing of “Insert Table of Figures” feature are shown in Table 6.
-
C. Benchmark 3
Here, we have taken some benchmark problems selected carefully from the existing literature [6, 24, 25] on pair-wise testing. Comparison of CA sizes generated by ABCHS-CAG with the existing algorithms for pairwise testing is done by executing the benchmark problems if the tool is publicly available otherwise they are compared based on the results reported in past. Table 7 and Table 8 shows the size and generation time of CA generated by the existing algorithms for the selected benchmark problems. ‘-‘ in Table 7 indicates that the result is unavailable. It is evident from Table 4, 6, 7 and 8 that ABCHS-CAG takes more time to generate CAs as compared to their greedy and meta-heuristic counterparts however, it generates smaller CAs as compared to their greedy counterparts whereas the results are better or comparable to the existing meta-heuristic techniques.
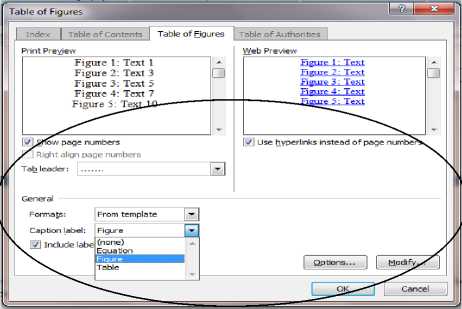
Fig.4. “Insert Table of Figures” feature in MS-Word
Table 5. Input parameters and their values of “Insert Table of Figures” feature.
|
Parameters |
Values |
|
Show page numbers |
Yes, No |
|
Include label and number |
Yes, No |
|
Use hyperlinks instead of page numbers |
Yes, No |
|
Tab leader |
0, 1, 2, 3 |
|
Caption label |
None, Equation, Figure, Table |
|
Formats |
From template, Classic, Distinctive, Centered, Simple, Formal |
Table 6. Comparison of MCA size/MCA generation time (in seconds) for “Insert Table of Figures” feature.
|
Jenny |
PICT |
Allpairs |
TVG |
ACTS (IPOG) |
CASA |
PWiseGenPM |
ABC-CAG |
ABCHS-CAG |
||||
|
avg |
best |
avg |
best |
avg |
best |
avg |
best |
|||||
|
26/ 0.046 |
26 |
27/ 0.056 |
26/ 0.141 |
24/ 0.059 |
24 |
24/ 0.54 |
24 |
24/ 0.015 |
24 |
24/ 0.96 |
24 |
24/ 0.76 |
Table 7. Comparison of MCA size
|
MCA Instance |
AETG |
TVG |
AllPairs |
PICT |
Jenny |
ACTS (IPOG) |
GA |
A CA ACOerfo rms ACOG algorith m. gorithm (ACA), which was inspired by AETG algorith m. a rily large N and1010 101010 101010 101010 101010 101010 101010 101010 101010 1010 |
PSO |
TS |
PPSTG |
CASA |
PWiseGen PM |
CS |
FSAPO |
ABC-CAG |
ABCHS-CAG |
|||
|
best |
avg |
best |
avg |
best |
avg |
|||||||||||||||
|
510 |
- |
50 |
47 |
47 |
45 |
45 |
- |
- |
- |
- |
45 |
38 |
39. 7 |
40 |
- |
- |
41 |
41.6 |
39 |
39.8 |
|
4534 |
- |
26 |
22 |
26 |
26 |
24 |
- |
- |
- |
19 |
- |
19 |
20 |
19 |
- |
- |
19 |
19.8 |
19 |
19.6 |
|
513822 |
20 |
23 |
20 |
20 |
23 |
19 |
17 |
17 |
17 |
15 |
21 |
15 |
16. 2 |
15 |
21 |
18 |
15 |
15.9 |
15 |
15.4 |
|
514431125 |
30 |
33 |
27 |
32 |
32 |
26 |
26 |
27 |
27 |
22 |
- |
22 |
23. 7 |
25 |
- |
- |
22 |
23.9 |
21 |
21.6 |
|
6151463823 |
34 |
40 |
34 |
38 |
40 |
36 |
33 |
34 |
35 |
30 |
39 |
30 |
30. 2 |
30 |
43 |
35 |
30 |
30.2 |
30 |
30.4 |
|
624929 |
- |
44 |
38 |
41 |
44 |
39 |
- |
- |
- |
36 |
- |
36 |
36. 4 |
39 |
- |
- |
36 |
36.2 |
36 |
36.8 |
|
655534 |
- |
63 |
53 |
59 |
56 |
56 |
- |
- |
- |
50 |
- |
47 |
49. 3 |
52 |
- |
- |
51 |
52.5 |
46 |
46.42 |
|
7161514538 23 |
45 |
49 |
43 |
46 |
50 |
43 |
43 |
43 |
43 |
42 |
49 |
42 |
42 |
42 |
51 |
- |
42 |
42.2 |
42 |
42.4 |
|
694327 |
- |
69 |
59 |
67 |
64 |
61 |
- |
- |
- |
51 |
- |
52 |
53. 23 |
59 |
- |
- |
51 |
51.7 |
51 |
51.3 |
Table 8. Comparison of MCA generation time (in seconds)
|
MCA Instance |
TVG |
AllPairs |
Jenny |
ACTS(IPOG) |
CASA |
PWiseGenPM |
ABC-CAG |
ABCHS-CAG |
|
510 |
0.479 |
0.013 |
0.309 |
0.003 |
3.608 |
11.4 |
123.708 |
38.63 |
|
4534 |
0.023 |
0.012 |
0.15 |
0.001 |
0.6785 |
2.76 |
37.2 |
24.09 |
|
513822 |
0.098 |
0.013 |
0.095 |
0.002 |
0.8145 |
2.95 |
47.1 |
5.62 |
|
514431125 |
0.435 |
0.016 |
0.202 |
0.015 |
3.15 |
13.74 |
74.9 |
12.43 |
|
6151463823 |
0.339 |
0.009 |
0.229 |
0.016 |
11.2 |
23.94 |
78.65 |
36.45 |
|
624929 |
0.397 |
0.009 |
0.247 |
0.016 |
2.21 |
11.52 |
180.8 |
67.03 |
|
655534 |
0.415 |
0.015 |
0.249 |
0.015 |
106.56 |
88.8 |
246.87 |
206.7 |
|
716151453823 |
0.254 |
0.016 |
0.383 |
0.016 |
1.44 |
12.3 |
66.24 |
49.56 |
|
694327 |
0.847 |
0.015 |
0.319 |
0.016 |
7.06 |
33.04 |
633.23 |
215.2 |
-
VIII. Conclusion and Future Work
In this paper, we have proposed a hybrid algorithm ABCHS-CAG, where the exploitation capability of ABC is improved by improvising the solutions using the three rules of HS: memory consideration rule, pitch adjustment rule and random selection. The performance of ABCHS-CAG compared and analyzed with respect to the existing literature on pair-wise testing. The experiments conducted on a set of benchmark problems show that the proposed strategy generates smaller or comparable CA as compared to its greedy and meta-heuristic counterparts.
In future, we plan to incorporate constraint handling features in ABCHS-CAG.
Список литературы A Hybrid Artificial Bee Colony and Harmony Search Algorithm to Generate Covering Arrays for Pair-wise Testing
- D. M. Cohen, S.R. Dalal, and M. L. Fredman, "The combinatorial design approach to automatic test generation," IEEE Software, pp. 83–87, 1996.
- K. Burr, and W. Young, "Combinatorial test techniques: table-based automation, test generation and code coverage," International Conference on Software Testing Analysis & Review,San Diego,1998.
- R. Kuhn, D. Wallace, and A. Gallo, "Software fault interactions and implications for software testing," IEEE Transactions of Software Engineering., 30(6), pp. 418–421, 2004.
- C. Nie, H. Leung, "A survey of combinatorial testing," ACM Computing Surveys (CSUR), 43(2), pp. 1-29, 2011
- Y. Lei, and K. C. Tai, " In-parameter-order: a test generation strategy for pairwise testing," In: 3rd IEEE International Symposium on High-Assurance Systems Engineering, p. 254–261, Washington, DC, 1998.
- M. B Cohen, C. J. Colbourn, P. B. Gibbons, and W. B. Mugridge, "Constructing test suites for interaction testing," ICSE, pp. 38-48, Portland OR, 2003
- C. Blum, "Hybrid metaheuristics in combinatorial optimization: A survey," Applied Soft Computing, 11(6), pp. 4135-4151, 2011.
- D. Karaboga,"An idea based on honeybee swarm for numerical optimization," Technical Report TR06, Erciyes University, Engineering Faculty, Computer Engineering Department, 2005.
- Z. W. Geem, J. H. Kim, and G. V. Loganathan, "A new heuristic optimization algorithm: harmony search. Simulation," pp.60–68, 2001.
- A. Hedayat, N. Sloane, and J. Stufken, "Orthogonal Arrays," Springer New York, 1999.
- G. Sherwood , "TestCover," http://testcover.com/pub/constex.php.
- A. W. Williams, "Determination of test configurations for pair-wise interaction coverage," 13th International Conference on the Testing of Communicating Systems, Ottawa, Canada, pp. 59-74, 2000.
- A. Hartman, and L. P. Raskin,"Problems and algorithms for covering arrays.,"JDM.,284 (1-3), pp. 149-156, 2004.
- N. Kobayashi, T. Suchiya, and T. Kikuno, "A new method for constructing pair-wise covering designs for software testing.," IPL, 81 (2), pp. 85-91, 2002.
- Y. Tung, and W. Aldiwan,"Automating test case generation for the new generation mission software system,"IEEE Aerospace Conference, pp. 431-437, 2000.
- J. Arshem, "Tvg,": http://sourceforge.net/projects/tvg.
- J. Czerwonka," Pairwise testing in real world: practical extension to test case generator," 24th Pacific Northwest Software Quality Conference, Portland, OR, USA, pp. 419-430, 2006.
- B. Jenkins,: http://burtleburtle.net/bob/math/jenny.html. Z.Wang, B. Xu, C. Nie, "Greedy heuristic algorithms to generate variable strength combinatorial test suite," International Conference on Quality Software. IEEE Computer Society. pp. 155–160, 2008.
- Z. Zhang, J. Yan, Y. Zhao, and J. Zhang, "Generating combinatorial test suite using combinatorial optimization," Journal of Systems and Software, vol. 98, pp. 191–207, 2014.
- Y. .Lei, R. Kacker, D. R. Kuhn, V. Okun, and J. Lawrence, "IPOG: A general strategy for t-way software testing," 14th IEEE International Conference and Work-shops on the Engineering of Computer- Based Systems-ECBS," Tuscon, AZ,USA, pp. 549-556, 2007.
- T. Shiba, T. Tsuchiya, and T. Kikuno, "Using artificial life techniques to generate test cases for combinatorial testing," 28th Annual International Computer Software and Applications Conference, pp. 72–77, IEEE Computer Society, 2004.
- L. Gonzalez-Hernandez, N. Rangel-Valdez, J. Torres-Jimenez, "Construction of mixed covering arrays of strengths 2 through 6 using a tabu search approach," Discrete Mathematics Algorithms and Applications, 4 (3),2012.
- H. Avila-George, J. Torres-Jimenez, V. Hernández, V. L. Gonzalez-Hernandez,"Simulated annealing for constructing mixed covering arrays," Advances in Intelligent and Soft Computing,vol.151, pp. 657–664, Springer Berlin , Heidelberg, 2012.
- B. S. Ahmed, K. Z. Zamli, "The development of a particle swarm based optimization strategy for pairwise testing," Journal of Artificial Intelligence, 4, pp. 156-165, 2011.
- B. J. Garvin, M. B. Cohen, M. B. Dwyer,"Evaluating improvements to a meta-heuristic search for constrained interaction testing," Empirical Software Engineering, 16(1). pp. 61-102, 2011.
- J. D. McCaffrey,"Generation of pairwise test sets using a genetic algorithm," 33rd Annual IEEE International Computer Software and Applications Conference," pp. 626–631, Los Alamitos, 2009.
- P. Flores, Y. Cheon, "PWiseGen: Generating test cases for pairwise testing using genetic algorithms,"International Conference on Computer Science and Automation Engineering, pp. 747 –752, 2011.
- P. Bansal, S. Sabharwal, S. Malik, V. Arora, V. Kumar, "An approach to test set generation for pair-wise testing using genetic algorithms," In: G. Ruhe and Y. Zhang (Eds.): SSBSE 2103, LNCS 808., pp. 294-299, Springer-Verlag, Berlin Heidelberg, 2013.
- B. S. Ahmed, T. S. Abdulsamad, and M. Y. Potrus," Achievement of minimized combinatorial test suite for configuration-aware software functional testing using the Cuckoo search algorithm.,"Information and Software Technology, 66, pp. 13–29, 2015.
- T. Mahmoud, B. S. Ahmed, "An efficient strategy for covering array construction with fuzzy logic-based adaptive swarm optimization for software testing use," Experts Systems with Applications, 42, pp. 8753–8765, 2015.
- J. Lin, C. Luo, S. Cai, K. Su, D. Hao, and Lu Zhang, "TCA: An efficient two-mode meta-heuristic algorithm for combinatorial test generation," In 30th International IEEE/ACM Conference on Automated Software Engineering (ASE), pp. 494-505, 2015.
- S. Sabharwal, P Bansal, N. Mittal, and S. Malik, "Construction of Mixed Covering Arrays for Pair-wise Testing Using Probabilistic Approach in Genetic Algorithm," The Arabian Journal for Science and Engineering, Springer, 2016.
- S. Sabharwal, P.Bansal and N.Mittal, "Construction of Strength Two Mixed Covering Arrays Using Greedy Mutation in Genetic Algorithm," International Journal of Information Technology and Computer Science (IJITCS), Vol. 7, No. 10, pp. no..23-34, September 2015, ISSN: 2074-9007 (Print), ISSN: 2074-9015 (Online), DOI: 10.5815/ijitcs
- Y. Jia, M. Cohen, and M. Petke, "Learning Combinatorial Interaction Test Generation Strategies using Hyperheuristic Search," ICSE, pp.540–550, 2015.
- P. Bansal, S. Sabharwal, N. Mittal and S. Arora,"ABC-CAG: Covering Array Generator for Pair-wise Testing Using Artificial Bee Colony Algorithm,"e-Informatica Software Engineering Journal, 2016.
- J. Stardom, "Metaheuristic and the search for covering and packing arrays," Master's Thesis, Simon Fraser University, 2001.
- G. Zhu, and S. Kwong, 'Gbest-guided artificial bee colony algorithm for numerical function optimization," Applied Mathematics and Computatio,. 217, pp. 3166–3173, 2010.
- D. R Kuhn, R. N. Kacker, and Yu Lei, "Practical Combinatorial Testing," NIST Special Publication, 800-142, 2010.


