A hybrid dimensionality reduction model for classification of microarray dataset

Published Online November 2017 in MECS

In recent years, developments in data possession ability, data compression and improvement of database as well as data warehousing knowledge have shown the way to the emergence of high dimensional dataset. Many data are irrelevant and redundant, giving rise to increase in the search space size and giving rise to complexity of processing the data. This curse of dimensionality is a key problem in machine learning. Hence dimensionality reduction is a dynamic research area in the area of microarray gene analysis, machine learning, data mining and statistics [1].

Dimensionality reduction as a pre-processing approach, it helps in removing redundant or irrelevant features from high dimension microarray dataset. Diagnosing and classifying cancer diseases based on innovative gene expression information is a challenge [2], microarraybased gene expression has become a realistic method in the prediction of classification and prognosis outcomes of diseases [3].

Cancer is the most deadly genetic disease; it arises either through epigenetic modification or changes leading to altered gene expressions information of cancerous cells. Currently, how to effect diagnose and classify cancer diseases based on new developed gene expression profiles are becoming an important challenge [2], microarray-based gene expression profiling has proven to be a promising approach in predicting disease classification and prognosis outcomes [3].

In this paper, the first step uses feature selection is employed, to produce sub-optimal results of gene selection on a Colon cancer microarray datasets. This paper aims at developing a feature selection algorithm that reduces the genes to a considerable amount and minimizes the complexity on further processing, pre and post diagnosis using one-way ANOVA feature selection. As a pre-processing step to machine learning, it is prominent and effective in dimensionality reduction, by removing irrelevant and redundant data, increasing learning accuracy, and improving result comprehensibility. Feature selection methods [4], [5], [6], tend to identify the features most relevant for classification.

The second step uses feature extraction dimensionality reduction by projecting the given datasets into a lower dimensional space and constructs new dimensions the relationships of the dataset. Principal Component Analysis (PCA) is used, which is a frequently used unsupervised approach and Partial Least Square (PLS), which is a widely used supervised approach for gene expression analysis of microarray data to further reduce dimensionality separately so as to get a more robust and efficient dimensional space.

In the third step, classification is carried out using Support Vector Machine (SVM). Their performances are studied on the classification of the extracted features.

This paper develops a hybrid dimensionality reduction model by imploring feature selection algorithm (One-Way-ANOVA) on colon cancer dataset to identify the most relevant features for classification [4], [5], [6], it reduces the dataset from 2001 to 416 attributes. The 416 attributes are passed to feature extraction algorithm using PCA and PLS separately to project the reduced datasets, into a low-dimensional space and create a unique dimension for the interaction of the dataset, it achieved 10 components and 20 components respectively. It trims down the data to a significant relevant quantity, and the complexity on supplementary processing, in other to enhance learning accuracy, and get a better result clarity. Classification is carried out using Support Vector Machine (SVM) and accuracy of PLS based reaches 98% and outperforms PCA based approach.

• II.    Related Works

Several studies have been proposed for dimensionality reduction of microarray data, using different techniques.

• [7] , applied a reduced dataset of genes by carrying out gene pre-selection with a univariate principle task, and subsequently estimated the upper bound of errors in Bayes, to sort unneeded genes resulting from preselection step. To prove their scheme K-Nearest Neighbor (KNN) and SVM classifiers were used on five datasets [7].

• [8]    Worked the innovation of Differentially Expressed Genes (DEGs) in microarray data, by building a precise and cost efficient classifier. T-Test feature selection method with KNN classifier was used on Lymphoma dataset to build the DEGs, the classifier accuracy was recorded.

• [9] , proposed variety forms of dimensionality reduction approach on a high-dimensional microarray data. Several feature selection and feature extraction processes seeking to eliminate redundant and irrelevant features, for innovative instances of classification, which can be accurate, were established.

• [10]    Proposed a cluster elimination and dimension reduction for cancer classification. ANOVA, PCA, Recursive Cluster Elimination (RCE) as a classification algorithm were implored by employing an innovative gene selection method. It reduces gene expression data into minimal number of gene subset.

• [16]    Proposed a feature selection based dimensionality reduction model on microarray biological data to improve the pre-evaluation information, the feature selection subset improved the data by using the top ranking pairs for features in the selection process, KNN and SVM were used in testing the classification results.

• [17]    Proposed and implemented a dimension reduction method for microarray datasets, using k-means clustering algorithms Laplacian eigen map and isomap methods were used to achieve clustering accuracy, the overall result showed that Laplacian eigenmap provides an improvement performance of redundancy than isomap.

• [18]    proposed the selection of combinations of features to classify a dataset due to the problem of the size of power set of features to search and ensuring choice of features, using targeted projection pursuit as a dimension reduction technique on a high dimensional data. TPP

classification was time efficient, but more work is still required to investigate the effect of output dimensionality.

• [18]    Considered feature selection as one of the most important preprocessing step in data mining and knowledge engineering. They produced a comprehensive list of problems solved using feature selection to serve as a valuable tool to practitioners and compared filter based

Research is still on for innovative techniques to select unique features for classification improvement. According to previous studies, there are several limitations as regards to the problem of developing efficient and effective classification models. This paper combines Feature selection using one-way ANOVA with feature extraction using PCA and PLS separately to enhance classification using SVM.

• III. Methodology

The propose system consists of modules: Feature selection, feature extraction, Classification and result modules. The colon cancer dataset loads as an input to the feature selection module where One-Way ANOVA algorithm is applied to the dataset. The input from the feature selection module is given to the feature extraction module, where the feature extraction are used separately, which is further classified by classification module using the Support Vector Machine and the result is displayed in the result module.

One-Way-ANOVA feature selection is combined with feature extraction methods ‘PCA and PLS’ as the data technique in microarray data analysis and support vector machine for classification technique. These techniques will be combined and used in constructing a model for the performance of classification. The methodology used in this study is as follows:

• •    Employment of one-way ANOVA feature selection with PCA features extraction and SVM classification in dimensionality reduction to improve classification performance.

• •    Use one-way ANOVA feature selection with PLS feature extraction and SVM classification in dimensionality reduction to improve classification performance.

Comparing our results in terms of ; accuracy, specificity, sensitivity, precision and time.

• A. Hybrid Approach

The propose system consists of a hybrid module; Feature selection and feature extraction for Classification to evaluate the performance of classification. Colon cancer dataset [11] loads as an input to the feature selection algorithm (One-Way ANOVA) algorithm. The input from the feature selection module is passed to the feature extraction and classified by using the SVM and the result is displayed in the result module.

The methodology used in this paper is as follows:

• •    Employ one-way ANOVA feature selection with PCA features extraction and SVM.

• •    Use one-way ANOVA feature selection with PLS feature extraction and SVM classification.

• •    Compare the performances in terms of; accuracy, sensitivity, specificity, precision and time, to improve classification performance.

class Y=j:

S.2 = V  ( x j   Z-^t=1V i

X J )²

N j

—

X : The grand mean of predictor X:

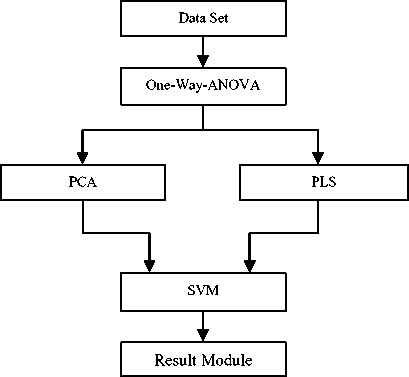
Fig.1. Technique Workflow

X =

J NX

J = 1 j j

N

The notations above are base on non-missing pairs of the sample and attribute of the dataset used in terms of (X, Y).

Calculating the p-value; Prob {F (J-1, N-J)>F}:

Where,

_F_ Z J = 1 ^N j ( X j — x )^2/( J — 1)

Z J = 1 ( N J — 1) x 2 /( N — 1)

Figure 1 shows a framework of dimension reduction for analyzing microarray data in this study. The colon cancer dataset [11] is passed into One-Way-ANOVA algorithm as a pre-processing process; the result is passed into the PCA and PLS as feature extraction algorithms, in other to fetch for the latent components before classifying using SVM model.

• B.    Experimental Dataset and Setup

A public available Colon cancer dataset by [11] was used for the experiment.

The system configuration used for the paper; Processor: iCore 2, RAM size: 4GB, Speed: 2.13 GHz, System: 64-bit, Operating System:  Windows 8 Pro, and

Implementation Tool: MATLAB R2015a

• C.    Feature Selection

In step 1, the gene dataset is computed with the use of One-Way-Analysis of Variance (ANOVA) as a feature selection method, it is a frequently used approach analyzing data and drawing interesting information based on P-Value, it is a robust technique; it presume all sample of a data to be distributed in general, having equal variance and independent [10]. The motivation is to carry out a one-way ANOVA feature by ranking the significant features through small values as 0.05 p-values and the classed numbers of features are further processed for selection of responsive data.

The following features apply:

N j =The number of cases with Y=j

X j =The sample mean of predictor X for target class Y=j

S ² _j =The sample variance of predictor X for target

F (J-1, N-1) is an indiscriminate variable which works with an F distribution with level of freedom J-1 and N-J. When denominator for a predictor is zero, position the p-value as 0.5. Predictor is classed by sorting the p-value in ascending order. If there is tie, sort F in descending order and if it still ties, sort N in descending order. Classification of features shows that 416 features were the most significant features correlated to the microarray data analysis out of 2001 features.

D. Feature Extraction

In step 2, the feature extraction module uses PCA and PLS separately on the microarray colon cancer datasets after passing through the One-Way-ANOVA Feature selection to paper the variation of efficiency performance.

Partial Least Square (PLS) is a procedure in modeling associations linking large piece of experimental variables using latent variable, it finds uncorrelated linear modification (latent components) of the selected predictor variables which comprises of response variables of high covariance [12].

PLS fetches the linear connection linking the response and descriptive variables y and X:

X = TP T + E x (4)

y = TC T + E_y                (5)

T signifies the scores (latent variables) P and C are loadings, and E x and E y are the outstanding matrices achieve by the original X and y variables.

Principal Component Analysis is suitable when there are measures achieved on a number of observed values; it is a procedure to determine the key variables in a multidimensional dataset explaining variations in the observations. It is very helpful for analysis visualization and simplification of high dimensional datasets [12]. The general formula for calculating the score of weight of

extracted components is;

C = Ь 11 ( X 1 ) + Ь 12 ( X ₂) + • - Ipp ( X p )        (6)

where;

C_T = the principal component 1 on subject’s score (the first component extracted)

b_tp = the regression coefficient (or weight) for experimental variable p, used in generating principal component 1

X_p = the subject’s score on experimental variable p.

Feature selection preserves data characteristics for interpretability, but discriminates power, with a lower and shorter training time as well as reducing overfitting. While, feature extraction has higher discriminating power and it controls overfitting when it is unsupervised, but losses data interpretability and also its transformation may be expensive.

• E. Classification

In step 3, the results for classification were computed using Support Vector Machine (SVM). SVM is a statistical knowledge theory for learning constructive procedure [13], it is used for classification tasks, and it uses linear models in implementing non-linear class boundaries by transforming input space using a nonlinear mapping into a new space. SVM produces an accurate classifier with less over fitting and it is robust to noise.

Assuming {(% _г, У) ), ..., (х _п ,у _п )} be a training set with x _Ti e R^d and у_t is the corresponding target class. SVM can be reformulated as:

Maximize:

E n     1 v^ n V^ n        z T

• i = 1 a i - 2 L i = 1 L j = 1 a i a j y i y j ⁽ xi , x j )     ⁽⁷⁾

Subject to;

En aiyi = 0 and ai > 0, i = 1,2,-••,n       (8)

A weighted average of the training features. αi is an optimization task of Lagrange multiplier and αi is a rank label. α′si are non zero values for every points in the margin and on the accurate plane of the classifier.

• IV. Results and Discussions

The proposed approach based microarray gene expression classification is implemented along by dimensionality reduction based technique. The system configuration used for our study;

Processor: iCore 2

RAM size: 4GB

Speed: 2.13 GHz

System: 64-bit

Operating System: Windows 8 Pro

Implementation Tool: MATLAB R2015a

This work was developed using microarray gene datasets of Colon Cancer [11], there are 2000 gene samples and 62 attributes.

In order to show the importance of feature selection and feature extraction as a dimensionality reduction method we have also performed the following series experiments on the SVM learning machine to reduce the bias caused by learning machines.

• (a)    One-Way-ANOVA a feature selection method, all the genes is to fetch the relevant information needed for classification.

• (b)    Result attained is passed into PCA as dimension reduction method to pre-process the result gotten, all the newly extracted.

• (c)    Result attained from One-Way-ANOVA is passed into PLS as pre-processing dimension reduction methods.

• (d)    All the newly extracted components for PCA are input into SVM

• (e)    All the newly extracted components for PLS are input into SVM.

• (f)    results of Classification SVM method are shown.

There are parameters for SVM which shows the performance results for our experiments.

The performances of the proposed methods are studied, in which the dataset is restructured after the evaluation of each steps. The details of restructured dataset are shown in Table 1

Table 1. Result Evaluations

Dataset	Features Selected (one-way-ANOVA)	Feature Extracted (PCA)	Feature Extracted (PLS)
Colon Cancer (2001x62)	416	10 Components	20 Components

In the paper, the methods used obtained reduced results shown in Table 1 above, it presents confusion matrices for the paper in terms of accuracy, specificity, prediction, training time and error for justification, which are illustrated to determine the performance in the figures below.

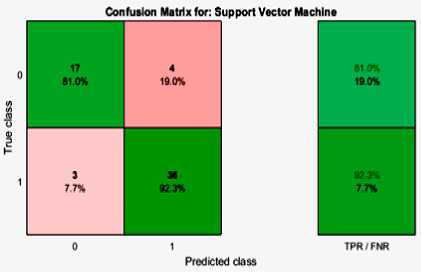
Fig.2. Confusion Matrix of Proposed Classification, using One-Way-ANOVA-PCA-Based Classification

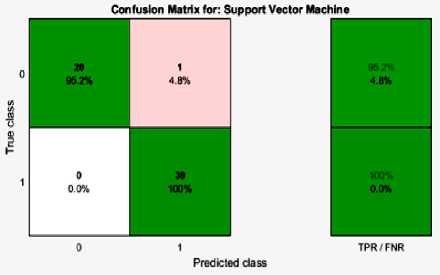
Fig.3. Confusion Matrice of Proposed Classification, using One-Way-ANOVA-PLS-Based Classification

Figure 2 and Figure 3 demonstrates the confusion matrices of the proposed paper, One-Way-ANOVA-PLS-Based and One-Way-ANOVA-PCA-Based methods achieved for the paper. The performance metrics are illustrated based on the confusion matrices and the reliability of the performances is discussed. The adopted terms are defined below [15]:

Sensitivity=TP/ (TP+FN) %(9)

Specificity = TN/ (TN+FN) %(10)

Accuracy = (TP+TN)/ (TP+TN+FP+FN) %(11)

Precision = TP/(TP+FP)%(12)

TP (True Positives) = correctly classified positive cases,

TN (True Negative) = correctly classified negative cases,

FP (False Positives) = incorrectly classified negative cases,

FN (False Negative) = incorrectly classified positive cases.

Sensitivity (true positive fraction) is the probability that a diagnostic test is positive, given that the person has the disease.

Specificity (true negative fraction) is the probability that a diagnostic test is negative, given that the person does not have the disease.

Accuracy is the probability that a diagnostic test is correctly performed.

Precision (Positive Predictive Value) is how many of the positively classified were relevant.

Colon [11] developed a classification method based on microarray dataset gene expression. To evaluate the performance of the proposed approach, one-way ANOVA uses p-value 0.05 as the hold out validation procedure to select relevant features. Feature extraction (PCA and PLS) methods that reduces dimensionality of the preprocessed data were compared using the SVM classification method.

Table 2 illustrates a comparative chart between the two methods used in terms of performance measures. The One-Way-ANOVA-PLS-Based    method    achieves necessary higher value in the dataset when compared to the One-Way-ANOVA-PCA method.

Table 2. Performance Measures of Proposed, PCA and PLS Based Method.

S/No	Performance Metrics	PCA-Based Method	PLS-Based Method
1	Training Time	2.973	0.28958
2	Accuracy (%)	83.33	98.33
3	Sensitivity (%)	92.31	100
4	Specificity (%)	80.95	95.60
5	Precision (%)	90	97.5
6	Area Under Curve	0.893773	1
7	Error (%)	11.7	1.67

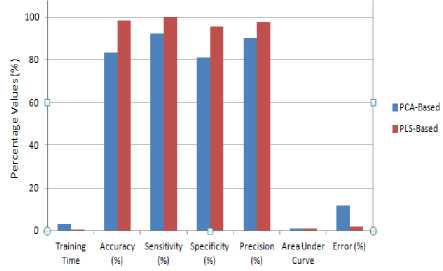
Fig.4. Maximum Performance Analysis of One-Way-ANOVA-PLS and one-Way-ANOVA- PCA SVM Classifier on colon cancer dataset.

The experimental results are very interesting; from the result it has shown that top components are important in achieving a better performance of microarray data. The reason can be found in the subsection of dimension reduction.

Feature selection is performed using One-Way-ANOVA, which shows great power to select feature subsets for classification; this can be seen from the experimental results. This method has been proved as one of the best feature selection method.

Feature extraction is performed using PCA and PLS. For PCA, 10 components are extracted by maximizing the variance of a linear combination of the original genes, and it did not maximize the discriminative power for the classifier SVM. For PLS, 20 components are extracted by maximizing the covariance between the responsive variables and the original genes, the top components of PLS is more important than PCA for classification.

The two types of dimensionality reduction methods “feature selection and feature extraction” are combines to achieve the purpose of this work. To reduce the dimensionality of microarray data One-Way-ANOVA features selection was combined with PCA and the result was compared with the combination of One-Way-ANOVA and PLS method. In general the result showed that One-Way-ANOVA and PLS outperforms One-Way-ANOVA and PCA due to the privileges PLS has gotten as a supervised learning method. The correlation made it attain an increase in accuracy function. More information was available to attain a correlation for accuracy. Hence the results indicate that PLS as a feature extraction method delivers better and greater in improving microarray performance.

PLS is superior to PCA as dimension reduction methods. The reason is simple, PLS extracts components by maximizing the covariance between the response variable y and the original genes X, which considers using the labels y and can be viewed as a supervised method. PCA extracts components by maximizing the variance of a linear combination of the original genes; it does not consider using the label y and can be viewed as an unsupervised method. This study improves the classification accuracy of SVM; this is a supervised task, PLS as a dimensionality reduction method is a supervised method is superior to PCA, an unsupervised method.

Features selected by different classifiers have minor difference, and results of prediction accuracy are also different. We have also conducted experiments on support vector machine (SVM), which show a more sensitive on high dimensional data sets compared to the state-of-art.

• V. Conclusion

This paper studied the performance of dimensionality reduction in microarray gene classification technique, using Colon Cancer datasets. The learning gritty on classification performance measures such as training time, accuracy, sensitivity, specificity, prediction, Receiver Operating Curve and Overall Error. PLS Based method showed a better performance than PCA-based method with 98.33% to 83.33% accuracy. Hence PLS based dimensionality reduction scheme is suitable for microarray gene classification as it extracts relevant and a reduced amount of information from the feature selection based technique. In future studies PLS can be compared with another feature extraction method with the aforementioned criteria. Another dataset will be a good avenue for further research of dimensionality reduction.