A Hybrid Multi-sensor Multi-target Tracking Scheme with MLE and ANFIS

Multi-target tracking technology in the military and civilian aspects have a wide range of applications such as ballistic missile defense systems, air and maritime surveillance and air traffic control [1-3]. With the developments of technology, a single sensor system cannot meet needs, and multi-sensor multi-target tracking [4-6] has become a hot research. For multi-sensor fusion multi-target tracking systems, the two most important issues are needed to be firstly solved, one is the matching problem of different sensors on the same objective measurements, that is to say, to identify which measurement from the different sensors is derived from the same target (homologous division) and then fusion of multiple measurements from the same target to produce the equivalent joint measurement of the same target; two is data association problem of the same sensor scans measured at different time, that is to say, the correct matching association problems of measurement and measurement, measurement and tracking. Currently, for multi-target tracking data association algorithm, the most classical method is the joint probabilistic data association algorithm (JPDA) [7-9], JPDA is theoretically the most perfect way, and particularly suitable for multiple target tracking in intensive mixed clutter environment, However, it is only suitable for single-sensor multi-target tracking situation, and as the number of targets and returns increase, the number of their joint assumption numbers of relevance is of the rapid growth, computing volume is of combinatorial explosion phenomenon. Therefore, for multi-sensor multi-target measurements, a hybrid scheme is proposed, which firstly partition of the same target, then applying for a single sensor multi-target tracking. JPDA algorithm [10-13] was proposed, which is based on adaptive neuro-fuzzy inference system and cheap JPDA algorithm, however, this method is only suitable for a single sensor. In this paper, a hybrid multiple sensor multiple target tracking system is presented, which applied maximum likelihood estimation, adaptively neuro-fuzzy inference system [14-16], and cheap JPDA algorithm.

In this paper, maximum likelihood estimation of multi-sensor multi-target system is applied to find homologous division from the same target, and then proceeds for each division of the same target from multiple measurements for fusion to obtain the same target observations, thereby the problem is changed into a single-sensor multi-target tracking. ANFIS is a fuzzy neural network in the framework of the fuzzy inference system. It is the neural network and fuzzy inference system which combines the advantages together with the faster and more accurate interpretation ability and excellent learning ability. This method is of fusion of data fusion, data association and target tracking to improve the tracking accuracy. Two typical scenarios for simulation, the simulation results show the effectiveness of the algorithm.

The paper is organized as follows. In Section II, different sensors data partition is described. In Section III, we give the cheap JPDA algorithm, and expound the idea for designing an MMT scheme. In Section IV, Adaptive Neuro-Fuzzy Inference System is introduced. Cheap JPDA Algorithm Based on Adaptive Neuro-Fuzzy Inference System is proposed in Section V. Performances and simulation results analysis for this MMT algorithm are given in Section VI. Conclusions are drawn in Section VII.

II. Different Sensors Data Partition

For a given measurement time k from some sensor systems, assuming there are N sensors to measure N targets, the number of sensors and the real targets is certainty, each sensor has m_n ( n = 1,2,-••, N_s ) measurements. Note the total sets of measurements are

A partition is known as feasible, if the following two conditions hold:

N T

и ^' = Z i=0

(2.8)

0 '      = ф ,i ф j , i , j = 0,1,2,-, N_T           (2.9)

Assuming all possible partition sets

Z N s = { Z n } 1 1 ,                                    (2.1)

where

Z n = { Z n .} m = 1 n = 1,2,-, N s                      (2.2)

which are measurement sets of the sensor n . In equation (2.1), the total number of measurements is N s m = S m n . n = 1

Target state equation and measurement equation is:

Xk = F k X k - 1 + Wk                            (2.3)

Z = H k X k + V k                          (2.4)

е=И '=

contain T₀ = { ^ } ^ ₁ feasible partition sets, where 9_q satisfying (2.8) and (2.9) is of a feasible partition. Conditions of feasible partitions only show that a measurement is from one target or false target. So we need to find the best one of the feasible partition sets. Maximum likelihood estimation (MLE) rule is used to get the goal, i.e. subjecting to the following likelihood function reaches maximum.

max q IT qQ

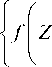
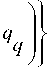
(2.10)

where, X denotes the state column vector of target, Z is for the measurement column vector, F is the state transition matrix, W , V are the uncorrelated Gaussian white noise, their covariance is Q , R , respectively,.

From (2.8) and (2.9) , we have

\ f (zNVq )= f (q'") f (q'1) Lf (q”) . f (q')= f (Z,„\ f (Z,.,) Lf (Z,^)

) =-------—    exp J - — eT .S 1e f ( n, in)     / _ v/2 \ Г pl ? n, i n, i e

(2n) Ven, A     1 2

(2.11)

(2.12)

As the corresponding relationship between measurements and targets is disorder, different sensors need association, this paper maximum likelihood estimation method to determine which measurements are from the same target in N sensors. Firstly, choosing a measurement from each sensor constitutes a target measurement vector:

^ l = { Z 1,„, Z 2, , 2 ,-, Z n, , n } i = 0,1,2,’”, N t      (2.5)

Where i = 0 for false targets set, i = 1,2,-••, N_T denotes true    N_T   goals collections,    d l =

{ Z . , Z ₂ . ,•••, Z _iN } represents the actual measured values     of     measured     random     vectors

^={ A, - 1 , Z 2. , 2 ,-, Z n , , i N, } , then, ^ ( i = ^0,1,2,-^{, N} T ) constitutes a possible partition of Z ^Ns :

■(2-6>

All possible Partition sets are written as:

® = {^ }I, °

Where p is the measure dimension, e denotes innovative information vectors of target i and sensor n from measurement Z      in time k , S is n,inn covariance matrix of innovative information.

Taking negative natural logarithm function of the likelihood:

NT

• - log Г f ( Z ^Ns ^ , ) ! = £ k ( ^ l)               (2.13)

^{L                J}    i = 0

Conversion request is made by (2.13) to find the smallest feasible partition.

^* = arg

= arg max f ZNs ^ 9q ET0 Г \      । q

NT min iS л(^'^

^{9 q e T} ® l i = 0

li

(2.14)

v ^ qq

In accordance with (2.14), the optimal solution is calculated, which is tfq = ^* ={^'i*} T^. The optimal feasible partition can get multi-sensor measurement sets from the same target or false target, then the same target measurement will be obtained by fusion these measurements, in order to update target tracking. Fusion method can be used such as the weighted average or un-weighted average, etc. When the sensor is the same type, we can use equal weights, but if different types of sensors or the sensor precision is not the same, and so un-weighted average can be used. Because of the fusion of the multi-sensor observation, the effects of the measurement noise are reduced, it can improve the tracking accuracy of the multi-target tracker.

• III.    Cheap JPDA Algorithm

JPDA algorithm is measured by calculating each of the probability associated with each track to be updated, and these probabilities as weights into the gate associated with the weighted average effective measurements to update the target state. Update equation based on Kalman filtering is written as xг  = x+ Kt X vt,                           (3.1)

—k I k     —k I k - 1        k     k ⁷                                                    7

where xˆt  is one step prediction state vector, Kkt denotes Kalman filtering gain, vkt represents the joint innovation information.

mkt vk = Z вЛ                          (3.2)

j = 1

where vk is the innovation information of track t and measurement j in time k , mt  represents the valid measurements number of track t , and в denotes the associated probability of track t and measurement j .

State covariance can be expressed as:

ˆt           kˆt                    k      tt

Pk I k = Po PI k-1 + |_1 Po t _ Pk I k + Pk

T

P k-1 = Fk-1 Pkt-1/k-1 (Ft-1)+ Q -1

P.ik =_I - KH _ P/k-1

Pk. = Kk mk Z k,vA v,)' - vi( v.1 (Kk)' (3.6) _ j=1                                   _ t       ˆt           t T t －1

^Kk   ^Pk I k - 1 ( ^Hk ) ( S k )                              ^(3.7)

Sk = HPI k-1 (Hk )T+Rk

In the standard JPDA algorithm, its associated probability calculation is very complicated, cheap JPDA (CJPDA) algorithm is proposed in order to reduce the complexity. Associated probability is calculated as follows:

p* =       G .

t   Wtk + Wj - Gk+B mkt

W. =ZG , j=1

N T

W j = Z G j.

t = 1

(3.10)

where, G ^k is the distribution of the innovation information, usually assumed to be normal, B depends on the clutter density constant.

• IV.    Adaptive Neuro-Fuzzy Inference System

Fuzzy inference system gives a very useful calculating framework, which is based on fuzzy set theory, fuzzy if-then rules and fuzzy inference. Among the fuzzy inference systems, Sugeno fuzzy model is used in a wide range, because of its high computational efficiency, and is optimal and adaptive. It gives the input and output data generated fuzzy rule based systems approach, which is depicted in Fig. 1.

Adaptive Neuro-Fuzzy Inference System (ANFIS) is functionally equivalent to a fuzzy inference system. Typically, when the human knowledge becomes into fuzzy systems, it gives the exact goal response. Therefore, we should estimate the optimal the parameters of fuzzy inference system. The main purpose of adaptive neuro-fuzzy inference system is to optimize parameters of fuzzy inference system based on the input and output data through the learning algorithm. A typical adaptive neuro-fuzzy inference system is depicted in Figure 1. Circle is fixed node, and box is adaptive node. For convenience, only two inputs and one output are assumed. In this paper, one-order Sugeno fuzzy model is used. For this fuzzy inference system, the following two fuzzy if-then rules are applied:

Rule 1: If x is A  and y  is B , then

Z\ = P\X + q^y + Г.                             (4.1a)

Rule 2: If x is A  and y is B , then

z2 = p2x + q2y + r2.                           (4.1b)

Where A_t , B , i = 1,2 are fuzzy sets, p_t , q_t , r are the system parameters, they are determined by the training process.

First layer: each node of the first layer using the following functions:

O i = p _A ( x ) , i = 1,2 ,                            (4.2a)

O i = р_в, _г ( y ) , i = 3,4                           (4.2b)

where ц_А ( x ) , m ( y ) can use any membership function.

Second layer:  each node calculated by the multiplication operator:

O i = Ma, ( x ) Mb, ( y ) , i = 1,2                        (4.3)

Third layer: the i th node calculated by a ratio formula:

w

O³ = w. =---- i —, i = 1,2

w , + w₂

(4.4)

Fourth layer: calculation formula as follows:

O i ⁴ = WZ = w ( px ⁺ qy ⁺ r i ) , i = ^{1,2           (}4.⁵⁾

Fifth layer: for all input signals weighted output:

O f = S Wizi i = 1

w_xz_x + w₂z₂ w + w₂

(4.6)

The learning algorithms of least square method (LSM) and back propagation method (BP) are used to get the parameters, they can train fuzzy systems fast and adaptively.

.fourth

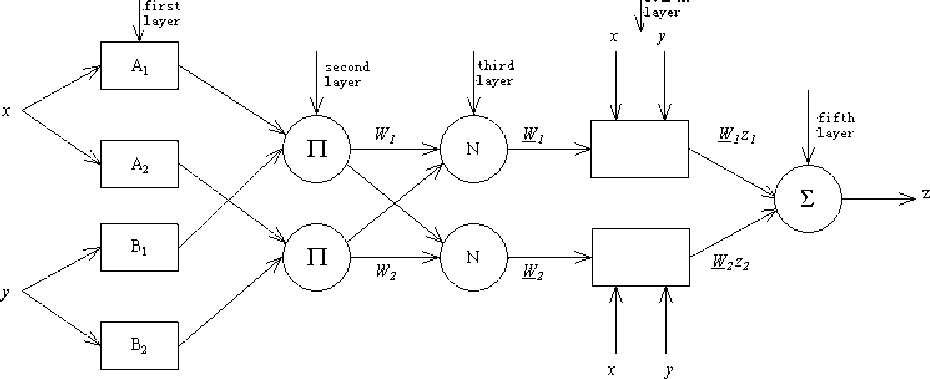
Fig. 1: Block diagram of adaptive neuro-fuzzy inference system

• V.    Cheap JPDA Algorithm Based on Adaptive Neuro-Fuzzy Inference System

ANFIS is applied to achieve updates of target. It involves two issues, first is the state prediction, the second is the update of the state. State prediction is similar to Kalman filtering algorithms [17-22], but state updates are different to Kalman filtering algorithm. The inputs of ANFIS are one step state prediction xˆt , measurement outputs zˆt, zˆt and joint innovation information v'k, vk-1. The outputs are the target states. They are the real states when training, but they are the state estimates when tracking. Firstly, a cheap JPDA algorithm based on formula (3.9) is used to calculate association probability в^ , and then calculate the innovation information vector vkt and prediction xˆt  , finally, the trained ANFIS is applied to update the target state. ANFIS needs training data, training data is used to determine the parameters of ANFIS, By subjecting to error between outputs of ANFIS and actual values in some criterion (such as LS rule) is minimized, then find the system parameters. The trained system is used to update the target state.

• VI.    Simulation results and discussions

To verify the proposed algorithm is effective and feasible, two scenes are investigated for simulation by using Matlab codes. Comparisons of tracking accuracy are made and analyzed between the cheap JPDA (CJPDA) algorithm and the hybrid algorithm presented in this paper. The root mean square (RMS) error is used as a measured criterion; the algorithm is run by 50 times in Monte Carlo simulation sensor. In this paper, the three sensors measuring system as an example for emulation, sensor standard deviation is 100 meters, in order to simplify the problem, regardless of coordinate conversion, and time calibration problems, the sampling period T = 1, 60 seconds track is considered, Supposing track initialization has been completed. Consider the two targets and three targets in cross movements, simulations are made in two typical scenarios, assuming uniform distribution clutter, its density is 0.2 / km 2, the initial target parameters in Table 1. Multi-sensor fusion multi-target tracking results are shown in Fig. 2 and Fig. 5. The RMS errors are shown in Fig. 3, Fig. 4, Fig. 6, Fig. 7 and Fig. 8.

Table 1: The initial position and speed of scenario 1, 2

Scenario	Target	x km	• x km/s	y km	• y km/s
1	1	1.57	0.14	7.97	0.16
	2	1.62	0.13	15.8	-0.17
2	1	1.15	0.23	2.25	0.19
	2	1.12	0.17	5.40	0.21
	3	1.45	0.22	11.5	-0.10

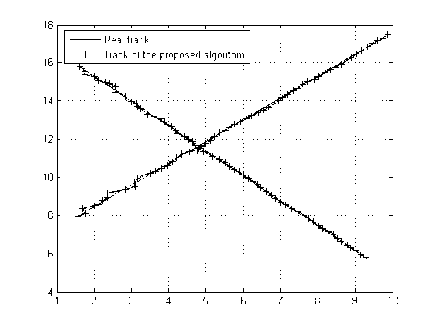
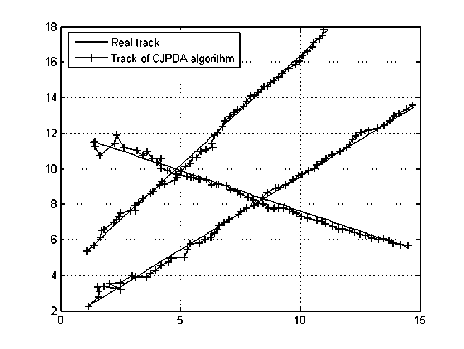
Fig. 2 and Fig. 3 give the results of tracking in two different scenarios. Fig. 2 (a) is the situation of the two cross-cutting targets, Fig. 5 (a) is the case for the three cross-cutting objectives, they are the fusion results of multi- sensor data according to the results of homologous partition, and then apply the single-sensor JPDA multi-target tracking algorithm to get tracking results, Fig. 2 (b) and Fig. 5 (b) is according to the proposed hybrid multi-target tracking algorithm for tracking results, that is to say, firstly, using multi-sensor data fusion, integrating the results, and then updating the target state, under the adaptive neuro-fuzzy inference system, to achieve results of multi-target tracking.

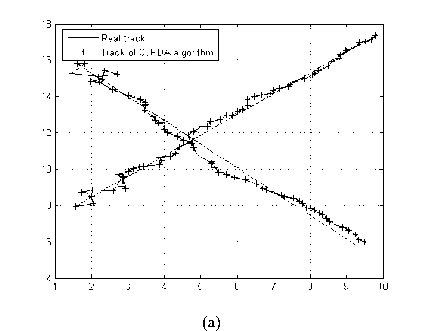
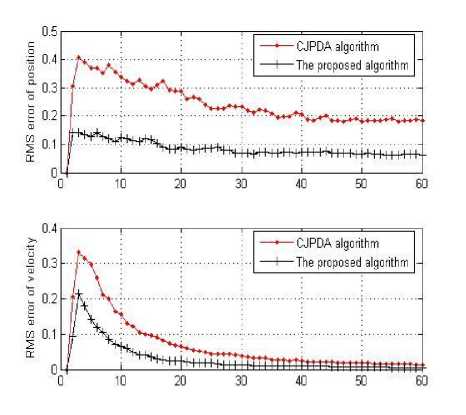
Fig. 3: The error of the target 1 in scenario

In Fig. 3 and Fig. 4, the root mean square error (RMS error) of target position and speed in scenario 1 is given according to the two different algorithms.

(b)

Fig. 2: Scenario 1, the multi-target tracking results of two different algorithms, CJPDA algorithm (a); the proposed hybrid algorithm (b)

(a)

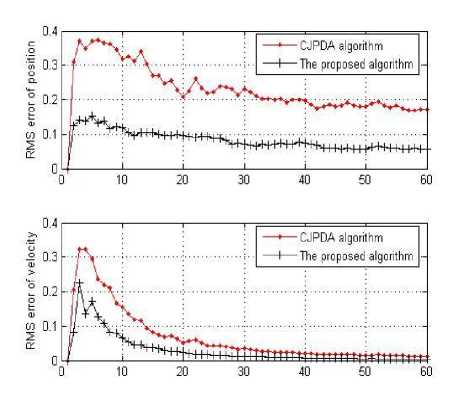
Fig. 4: The error of the target 2 in scenario 1

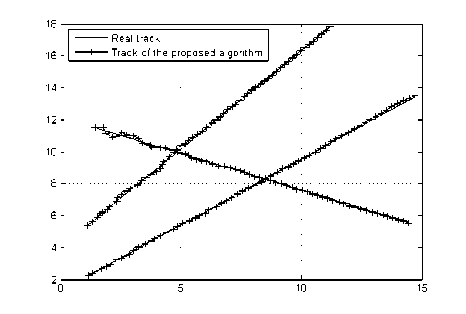
(b)

Fig. 5: Scenario 2, the multi-target tracking results of two different algorithms, CJPDA algorithm (a); the proposed hybrid algorithm (b)

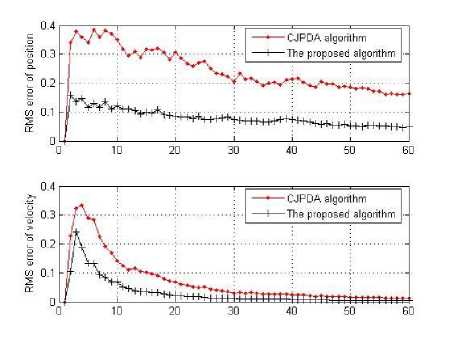
Fig. 8: The error of the target 3 in scenario 2

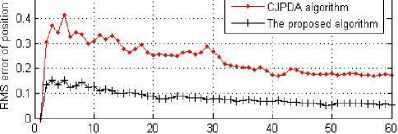
In Fig. 6, Fig. 7 and Fig. 8, the root mean square error (RMS error) of target position and speed in scenario 2 is given according to the two different algorithms. From the results, whatever two targets or three targets, we can see that the proposed algorithm effectively reduces the tracking error and improve the tracking accuracy.

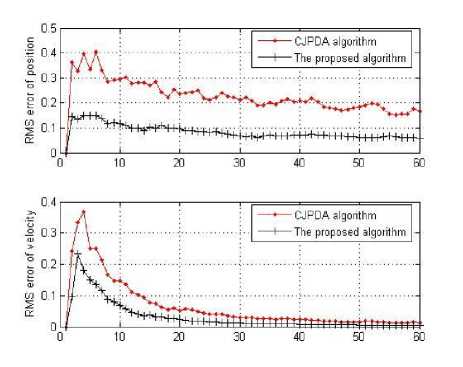
Fig. 6: The error of the target 1 in scenario 2

• VII.    Conclusions

0.5

In this paper, a hybrid multi-sensor multi-target tracking method was presented based on the analysis of the traditional single-sensor multi-target tracking in the joint probability algorithm. First, maximum likelihood estimation was used to find homologous partitions of multi-sensor data, second, measurements from the same sensors were fused, third, adaptive fuzzy neural inference system was applied to update and modify multiple target track based on the fused measurements results, finally, the multi-sensor multi-target tracking algorithm was achieved. The hybrid multi-sensor multi-target tracking algorithm effectively integrated multi-sensor fusion, data association, maximum likelihood estimation, and adaptive fuzzy neural inference system. The method did not combine JPDA algorithm and Kalman filtering, and adaptive neural fuzzy inference system replaced it. Two typical multi-sensor multi-target tracking system scenarios were simulated to test the proposed algorithm, the experimental results verified the effectiveness of the algorithm.

Acknowledgments

This work was financially supported by the Natural Science Foundation Project of CQ CSTC of China (grant No. CSTC2011jjA40033, grant No. CSTC2012jjA00037) and Project was Supported by Scientific and Technological Research Program of Chongqing Municipal Education Commission (Grant No.KJ120829).

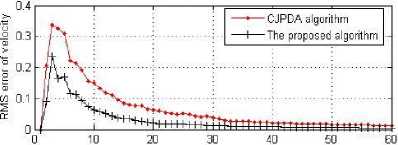
Fig. 7: The error of the target 2 in scenario 2