A method for determining the thermal resistance of a multilayer package of thermal insulation textile materials under blowing conditions

Original article

Technical fiber materials and webs are widely used in construction, industry and other sectors of the economy. They can be made of various materials such as glass fiber, basalt fiber, ceramic fibers, mineral wool and others. These materials, as a rule, consist of micro and nanoscale fibers, have a high thermal insulation ability, which allows them to be used for effective thermal insulation of facades and other building elements. In multilayer building structures, fibrous materials and technical fabrics [1–2] perform not only the function of thermal insulation, but also protection from moisture [3] and noise. They can be applied both as insulation for external walls and roofs, and for internal partitions and ceilings. In addition, these materials can be used to create ventilated facade systems, which can improve the thermal protection properties of the building [4–5] and reduce energy consumption for heating and air conditioning. Technical fiber materials and webs are also widely used in industry for thermal and acoustic insulation of pipelines, apparatus and equipment. They can be manufactured in different structures and densities, allowing the selection of the most suitable material for a particular application. Thus, technical fiber materials and webs are important elements in construction and industry. Their high heat-insulating,

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS sound-insulating and moisture-protective properties make them indispensable in creating comfortable living and working conditions in buildings and structures.

When designing and calculating multilayer building structures such as walls, roofs, ceilings and other building elements, it is necessary to take into account the thermal insulation properties of each of the layers. However, in reality, the contact between layers is discrete, resulting in contact thermal resistances in the contact zones of individual layers. These resistances can significantly affect the heat transfer [6–7] through the structure and hence its thermal efficiency. To account for contact thermal resistances in the contact zones of individual layers in multilayer structures, it is necessary to carry out thermal calculations taking into account the thermal properties of each layer and heat losses in the contact zones between them. In addition, such factors as the thickness of each layer, material density, thermal conductivity coefficient [8-9], temperature gradients and other parameters [10-11] should be taken into account. It is important to note that contact thermal resistances can have both positive and negative effects on the thermal efficiency of a structure. For example, in some cases, the presence of contact resistances can reduce heat loss through a structure and improve its efficiency [12]. In other cases, the presence of contact resistances can lead to poorer thermal efficiency and increased energy consumption for heating or air conditioning. In this regard, consideration of contact thermal resistances in the contact zones of individual layers in multilayer building structures is an important step in their design and calculation. This allows to optimize heat transfer through the structure, increase its thermal efficiency and reduce energy consumption for heating or air conditioning. It inevitably leads to a temperature jump at the contact points and to an increase in the temperature difference, which cannot be neglected (especially if the local heat flux density is significant). The heat flux at the approach to the contact is separated: one part goes through the air gap and the other part goes through the spots of actual contact between the fibers. The first thermal resistance depends on the thermal conductivity of the air medium and the size of the gap, since in most cases convection does not develop in the gaps, it has a surface character. The second resistance, on the other hand, has a volumetric character. In a thermal circuit both these resistances are included in parallel, so their inverse values (otherwise thermal conductivities) are summed up. It is especially important to take into account contact resistances when calculating the dynamics of temperature fields in multilayer envelope structures [13–15].

According to the phenomenological theory, the concept of contact thermal resistance is conditional and is not limited only by the presence of the interface. Contact thermal resistance describes a phenomenon in which an external heat flux density causes a potential difference at the interface of two different materials. However, contact thermal resistance can manifest itself not only at the interface of phases, but also within the same phase in the presence of micro and nanostructural structural defects. These defects can be caused by various factors such as the presence of dislocations, impurities and other inhomogeneities in the crystal structure. Contact thermal resistance is an important parameter for understanding the thermal properties of materials and can affect the performance of heat transfer devices such as heat exchangers and thermoelectric devices. In addition, contact thermal resistance can be used to measure various physical parameters of materials such as thermal conductivity and temperature gradients. Thus, the concept of contact thermoresistance has wide applications in various fields of physics and materials science and is not limited to the presence of an interface. Its understanding and study is important for the development of new technologies and improvement of existing methods of measuring physical parameters of materials. But in practice, the introduction of the concept of temperature jump at the boundary of two layers has some advantages because its magnitude can be easily determined experimentally by linear extrapolation of the temperature distribution in a multilayer body [13].

Contact resistance is most easily found in experiments using the stationary heat flow method, although in some cases it can be evaluated analytically using a theoretical analysis of model contacts [13, 14].

In order to reduce the energy intensity of the gross domestic product, interest in the rational consumption of thermal energy has increased [16]. To do this, the energy saving program [16] provides for an increase in the heatshielding characteristics of external envelopes [17, 18] of public, residential and industrial buildings.

Selection of appropriate thermal insulation coatings [19] as enclosing structures in buildings is determined by taking into account the following factors such as temperature and humidity conditions of the environment, physical properties of the textile material, including its moisture and air permeability, as well as thermal resistance, the location of construction [20–22].

MATERIALS AND METHODS

Building envelopes in the form of a package, consisting of textile sheets, are under the influence of an air flow directed perpendicular to the wind-affected surface. The paper presents the results of a study of the heat-protective characteristics of textile bags blown by an air stream with a velocity directed along the normal to their surface.

Fig. 1 shows a scheme of an ‘n’ number of textile fabric layers under the influence of the constant flow of a thermal fluid. The model includes the following layers:

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

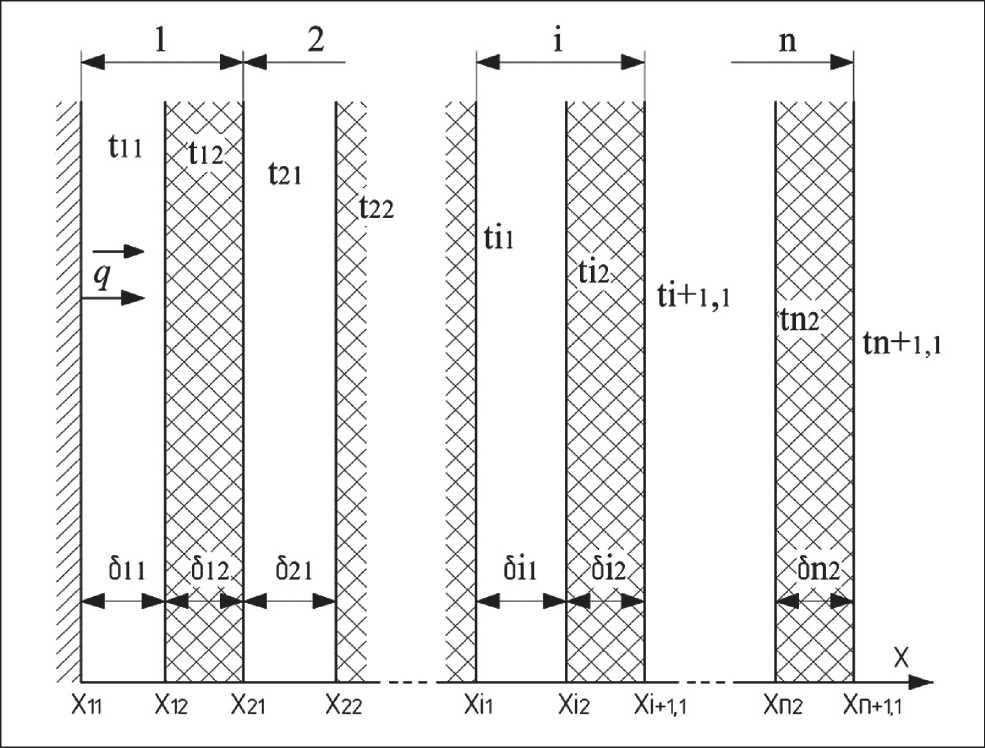
Fig. 1. Scheme of thermal-insulating layers of the package

the first layer, which is internal and is located near the impermeable surface; the ‘i’ layer; and partially the second, outer ‘n’ layer and the surrounding layer of air defined by this formula: x > xn+1,1. The layers of textile fabric have several thickness parameters of material: δi2 and an air gap: δi1; heat flux density vector: q on an impenetrable surface: (x = x11+0) numerically equals to q in axis direction x, flow rate: w air affecting the package; temperatures on the inner surface of the layer, as well as on the surface of the textile fabrics inside it and on the surface of the package itself, are indicated, respectively, as: ti1, ti2 and tn+1,1. The air flows opposite to the heat flow. The speed of the air passing through layer ‘i’ is set and is constant inside it [22]. Due to the insignificant thickness of the air layer, the normal to the surface components of the flow velocity of the thermal fluid in the gap can be represented by the Taylor series wi(x) = wi–mi·(xi2–x),                              (1)

where m_i = ( w_i – w_{i –1})/δ _{i 1}.

Figure 2 shows a graph of the velocity through the layers of textile fabrics forming the package.

According to the source [23], heat transfer is determined by adding an effective coefficient of thermal conductivity to the energy equation, which transfers heat due to the thermal conductivity of air in the material and radiation.

The heat flux affecting the model is considered onedimensional, according to Fig. 1 from left to right, heat is transferred by radiation and heat conduction, and from right to left only by convection. Under the conditions of a one-dimensional problem, when the following conditions are met: w _x = – w , w_y = w _z = 0, d_t / d _x = f ( x ), d_t / d_y = d_t / d_z = 0, then for the layer ‘i’, we can write the energy equation differentially, which will take the following form:

Л1 [^^] = -c 〃 • •叫 (x)[^^] . (2) 厶 2 厶

Between layers ‘i’ and (i-1) within a package of textile fabrics, the boundary conditions maintain the equality of heat fluxes and temperatures at their boundary:

t_{i 1} ( x_{i 1} ) = t_{i 1} ,

巧='丸" "")h] +a 〃 Pi -02 ),

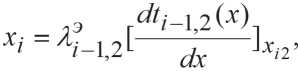
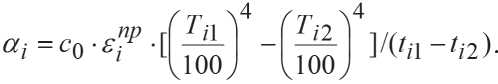
MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

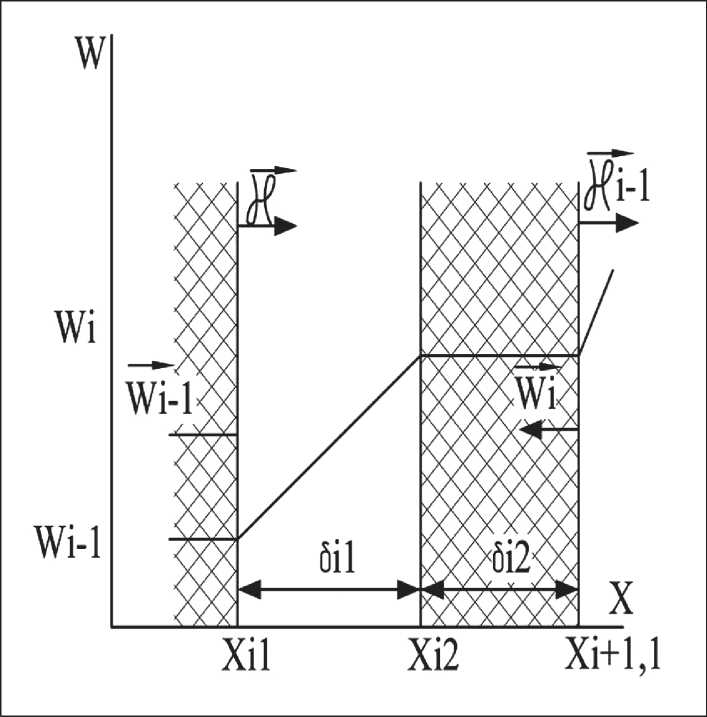
Fig. 2. Graph of the speed of the air flowing through the layers of textile fabric forming a package: w_i – air speed in the layer of the thermal fluid flow; w ( x ) – speed reduction in the air layer ‘i’ between the webs of textile material of ‘i’ and (i–1); – the density vector of the radiation-conductive flow along the inner surface of layer ‘i’ of the package

When considering the boundary between layers ‘i’ and (i-l), the value x_i is their conductive heat flux, and α _i – is the coefficient of heat transferred by radiation between the layers of material ‘i’ and (i-1) on a flat interlayer.

.                                  (7)

弓 к J—1,2 ⁶z2

Here: ε _i ^np , ε _i–1,2 , ε _i2 – correspond to the reduced degree of emissivity of the interlayer at the border of (i-1) and ‘i’ layers within the given package of textile fabrics; T_i – absolute temperature, [К].

According to the assumptions above, the differential form of the energy equation for the ‘i’ layer of the material will be similar to the form of the porous layer equation [24]:

.           (8)

Boundary conditions characterize the equality of heat fluxes and temperatures between the given materials of the package and the air gap of the ‘i’ layer:

t_{i 2}( x_{i 2}) = t_{i 2},

-Al [山纟;)]占 2 + a 厂(/汀- 02)

3 北 2 ( x)]

.

Equations (2) and (8) refer to linear differential equations of the 2nd order, but the latter equation comes with constant coefficients, and their solutions can be represented as:

,   (11)

a,[exp (—片])+。乂沙 2 - Ул)]

勿出 2 【 ехрб/)+4О ； 2— 为)]

61(%) = *2—:--------7--

A_j2Wj [ехр^_я) + Д (у/2 -J/i)]

,                             (12)

,                          (13)

where D_i = [πα²/(2λ _{i 1}·c _{i 1}·ρ _{i 1}· m_i ]^0,5; variable y = w_i ( x )/ J2 mi- . a 〃 , and between the layers y .1 = w, 」/ J2 mi- a 〃 and y ₂ = w, /J2 mi-. a 〃 ; a,1 — coefficient of thermal diffusivity in the air gap a ₁ = λ ₂ ^Э /(c ₁·ρ ₁); integral values yʹ are presented according to [25]. Value χ ₊₁ is calculated by the recursive formula, provided that χ = q :

exp(_y/) + 。(屹-%)

勿+1 = Xi--2--------；----；— • ехР(-Уц) + Dj(y'i2 - V/l)

.                                     (14)

l 生 2 丿

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

Using equations (11) and (12), we can determine the temperature difference ∆ t at the boundaries of the air gap or material, according to the formula R = ∆ t / q thermal resistance can be represented as:

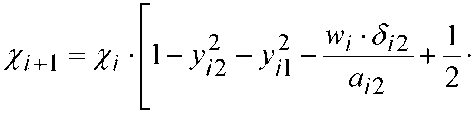
R] = Z 少乂 »2 -力 1)

,

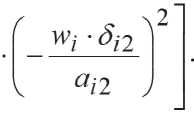
R    力厂? 2  exp (-靖)+ 2 ( 屹-及)

q-Wj ■ Л^₂ ехр(-у ， ) + 2О ； 2-%)

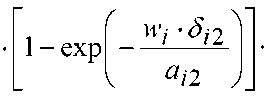
Thermal resistance to heat transfer from the outer surface of the package of textile fabrics to the environment can be calculated by the formula: R_{n +1} = χ_{i +1}·[ q (α _p + α _k )]^–1, when the heat transfer coefficient can be calculated by equation (6) when replacing T ? _+1,2 and t_{n +1,2} on ambient temperature, and then instead of ε _i ^np substitute the degree of blackness of the outer material included in the package we are considering. According to the formula of G.N. Kruzhilin [22], it is possible to calculate the coefficient of convective heat transfer for the front air flow point:

Nu = 1,04·Re^0,5·Pr^0,33.

The thermal resistance of the entire package consisting of textile fabrics is determined from the sum of the thermal resistances of the individual materials included in its composition, air gaps and thermal resistance of heat transfer to the environment.

Next, we analyze the passages to the limit in the obtained formulas. In layers where air velocities are insignificant, it can be represented as y_{i 1} y_{i 2}< 0,02 and w_iδ_{i 2}/ a_{i 2}< 0,1, after that, formulas (14), (15) and (16) are simplified by expanding into a series of errors by more than 1%, then the equation for calculating the corresponding thermal resistance will take the following form:

e   1-2 乃](乃 2 -乃 1 )

"    +[1-2 乃 1( 乃 2 -乃 1)]

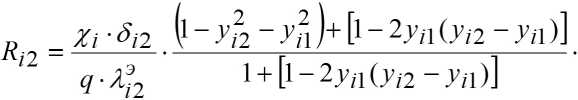
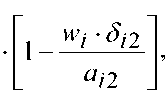
Two limiting transitions are possible, the first one is carried out at w_i → 0; from equations (14)–(19) it is possible to derive the following dependencies describing the heat transfer during the absence of airflow:

χ_i = q , R_{i 1} = 1/(α _i + λ _{i 1}/δ _{i 1}), R_{i 2} = δ _{i 2}/λ _{i 2} ^Э . (20)

The second limit transition occurs at high flow rates of the medium. Provided that material ‘i’ included in the package has high air permeability w_iδ_i / a_i > 5, then, according to equation (14), we can make: χ_{i +1} = 0 with an error of no more than 1%. The thermal resistances of the ( i +1) layer and subsequent layers with a higher number acquire a value equal to zero, and the temperatures in these layers become identical to the ambient temperatures, which corresponds to curve 5 in Fig. 3. Under such conditions, the heat-protective mechanisms of materials are reduced to wind-protective ones, and therefore the expediency of using a wind-protective layer becomes apparent. Building structures can serve as an example. The usage of a low-permeable layer contributes to the effectiveness of thermal protection functions of the other layers of the package.

RESULTS AND DISCUSSION

To apply this calculation of thermal resistance to construction objects, it is necessary to determine the air permeability of individual layers [26, 27] included in the package under the influence of natural airflow, and also to determine the patterns of changes in the thickness of the air layers. Since these values are initially unknown, we must resort to using the dependence of air permeability on the heat-shielding properties of the heat-insulating package. To solve the problem, we use a rational assumption from a physical point of view, but not proven empirically, that the flow rate of the medium in the ‘i’ layer is proportional to its air permeability and the dynamic pressure of the air flow of the medium, retained by the materials in the package:

w_i = b_hi ·ρ _i ( w_{i +1}² – w_i ²)/2 h_i , (21)

where h_i – is pressure fluctuation, which was determined at air permeability: b_hi . A similar formula was used by P.A. Kolesnikov [28], but the change in the thickness of the interlayers during the calculations

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

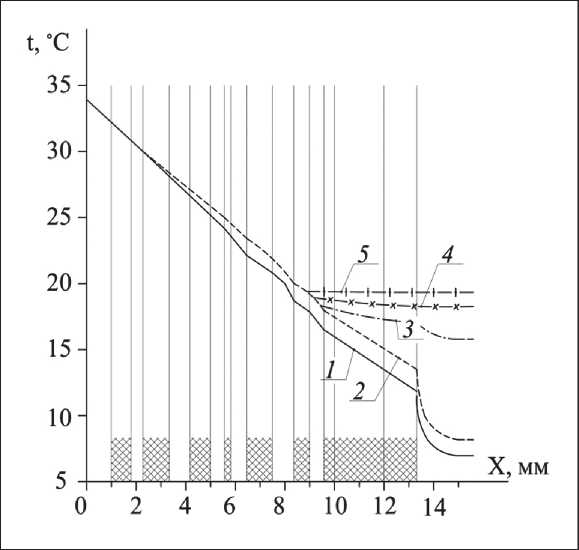
Fig. 3. The layout of the temperature curves obtained by calculation: 1 – w _∞ = 0, a_i = 0; 2 – w _∞ = 0, a_i ≠ 0; 3 – w _∞ = 4 м/с, a_i ≠ 0;

4 – w _∞ = 10 м/с, a_i ≠ 0; 5 – w _∞ = 20 м/с, a_i ≠ 0

was not taken into account. Fig. 3 shows the layout of the temperature curves, with the ones outside of the scheme calculated conditionally. During calculations, the method of successive approximations was used and the temperature curves were used as the initial temperature distribution under the condition that the air was considered to be stationary, and there was no heat transfer due to radiation in the air gap.

According to the diagram presented on Fig. 3, the decrease in the thermal resistance of the package is affected by an increase in the speed of the airflow. Along the curves in Fig. 3, both of the previously described cases can be traced. As shown on the diagram, in the inner layers of the package, the temperature curves are close to coincidence; this phenomenon can be caused by the low speed of the air flow. Curve 5 also indicates that with an increase in the speed of the airflow, the thermal resistance on the outer surface of the package decreases.

CONCLUSION

– The paper considers a non-standard approach, and provides equations for calculating the thermal resistances of both individual layers and the thermal insulation package as a whole, under conditions of a frontal air flow.

– It is noted that during real tests of the heat-shielding package, the thickness of the air layers will decrease, and the values of penetration of the cold airflow into the material will become higher;

– Therefore, this approach more reliably reflects the main regularities of heat transfer through a heatshielding package under ambient wind-blowin conditions, thereby leading a complicated solution of the problem to a much simpler research of air permeability and deformation of the layers within the package.