A Method for Solving Fuzzy Transportation Problem (FTP) using Fuzzy Russell's Method

Published Online January 2013 in MECS

• I.    Introduction

  In Mathematics and Economics, transportation theory is a name given to the study of optimal transportation and allocation of resources. The problem was formalized by the French Mathematician Gaspard Monge in 1781. Tolstoi was one of the first to study the transportation problem mathematically. The transportation problem (TP) refers to a special class of linear programming problem. When the theory of fuzzy sets was first introduced by Zadeh[18].

The transportation problem can be modeled as a standard linear programming problem, which can then be solved by the simplex method. In a typical problem a product is to be transported from m sources to n designations and their capacities are a 1 , a 2 ….a m and b 1 , b 2 …b n respectively.

In addition there is a penalty c_i j associated with transporting unit of product from source i to destination j. This penalty may be cost or delivery time or safety of delivery etc.

A variable xij represents the unknown quantity to be shipped from source i to destination j. Let ai be the amount of the product available at origin i and bj be the amount of the product required at destination j.

If shipping cost, are assumed to be proportional to the amount shipped from each origin to each destination so as to minimize total shipping cost turns out to be a linear programming problem. A fuzzy transportation problem is a transportation problem in which the transportation costs, supply and demand quantities are fuzzy quantities. Most of the existing techniques provide only crisp solutions for the fuzzy transportation problem. Shiang-Tai Liu and Chiang Kao [14],Chanas et al. [3], Chanas and Kuchta [2], proposed a method for solving fuzzy transportation problem. Nagoor Gani and Abdul Rezak [11] obtained a fuzzy solution for a two stage cost minimizing fuzzy transportation problem in which supplies and demands are trapezoidal fuzzy numbers. Pandian et al. [13], proposed a method namely, zero point method, for finding a fuzzy optimal solution for a fuzzy transportation problem where all parameters are trapezoidal fuzzy numbers. Amarpreet kaur[1] proposed a new method for solving fuzzy transportation problem by assuming that a decision maker is uncertain about the precise values of the transportation cost, availability and demand of the product. In many fuzzy decision problems, the data are represented in terms of fuzzy numbers.

In a fuzzy transportation problem, all parameters are fuzzy numbers. Fuzzy numbers may be normal or abnormal, triangular or trapezoidal. Ranking method is used to change the fuzzy number into crisp form. The method for ranking was first proposed by Jain [8]. Yager [17] proposed four indices which may be employed for the purpose of ordering fuzzy quantities in [0, 1]. Further references in this direction can be found in [4-5, 9-10]. Ranking function is used in different areas of fuzzy optimization.

In real life, there are many diverse situations due to uncertainty in judgments, lack of evidence etc. Sometimes it is not possible to get relevant precise data for the cost parameter. This type of imprecise data is not always well represented by random variable selected from a probability distribution. Fuzzy number may represent this data.

The aim of fuzzy transportation is to find the least transportation cost of some commodities through a capacitated network when the supply and demand of nodes and the capacity and cost of edges are represented as fuzzy numbers.

There are many methods to find the basic feasible solution, such as North–West Corner Rule, Row Minima Method Column Minima Method, Matrix Minima Method (Lowest Cost Entry Method), Vogel’s Approximation Method (Unit Cost Penalty Method) (VAM), Russell’s method. Here we use a new method named as Fuzzy Russell’s method for solving Fuzzy transportation problem.

Fuzzy Russell’s method (Tze-San lee [16]) is probably the best one of the following reasons:

• (i)    It generates a near-optimal initial feasible solution,

• (ii)    It simplifies the overall computer code to program it.

This research paper has five sections. In section one is introduction and the development of Fuzzy Transportation problem.

In section two, we just recall the basic concepts and yager’s ranking method. In the third section we proposed a new computational procedure for fuzzy Russell’s method. In section four, a numerical example is provided to illustrate the algorithm developed in this research paper. Finally we give conclusion in section five.

• II.    Preliminaris

• 2.1    Fuzzy Number

In this section the basic concepts of Fuzzy number, Trapezoidal fuzzy number, Properties of Trapezoidal number, Fuzzy Sets, Crisp Set are recalled.

A real fuzzy number a is a fuzzy subset of the real number R with membership function ц_й satisfying the following conditions,

• >    Ц~ is continuous from R to the closed interval [0,1]

• >    Ц~ is strictly increasing and continuous on [a₁,a₂]

• >    Ц~ is strictly decreasing and continuous on [a₃,a₄]

• 2.2    Trapezoidal Fuzzy Number

A fuzzy number A = ( a , b , c , d ) is said to be a trapezoidal fuzzy number if its membership function is given by,

Г о

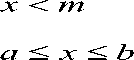
M a =i

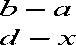
d — c

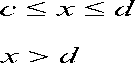
Ma (X)

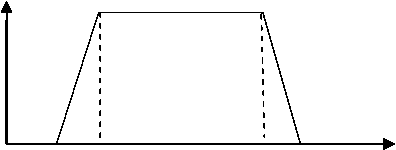
0 a b               c d      X

Fig. 2.1: Trapezoidal Fuzzy number

• 2.3    Properties of Trapezoidal Fuzzy Number

• •    Trapezoidal fuzzy number A = (a, b, c, d) is said to be non negative trapezoidal fuzzy number if and only if a-c >  0.

• •    A trapezoidal fuzzy number A = (a, b, c, d) is said to be zero trapezoidal fuzzy number if and only if a = 0, b = 0, c = 0, d = 0.

• •    Two trapezoidal fuzzy numbers A =(a₁,b₁,c₁,d₁) and A ₂ = (a₂,b₂ , c₂,d₂) are said be equal i.e. A = A , if and only if a 1 = a 2 , b 1 = b 2 , c 1 = c 2 , d 1 = d 2 .

• 2.4    Fuzzy Set

• 2.5    Crisp Set

A Fuzzy set A is defined as the set of ordered pairs (X, p , ( X )) ,where x is an element of the universe of discourse U and ц_л( X) is the membership function, that attributes to each X E U a real number _E [ 0,1 ] , describing the degree to which X belongs to the set.

Example:

Let X = {a, b, c, d }, Define g A : X ^ [0,1] as follows:

µ A (a) = 0, µ A (b) = 0.4, µ A (c) = 0.6, µ A (d) = 1

Then the class,

A = {(a, 0), (b, 0.4), (c, 0.6), (d, 1)} is a fuzzy set on X.

A crisp set is a special case of a Fuzzy set, in which the membership function only takes two values, commonly defined as 0 and 1.

2.6 Arithmetic Operation [7]

Let A 1 and A 2 be two trapezoidal fuzzy numbers parameterized by the quadruple ( a^ , _a , a ₃, a^ ) and ( b_x , b , b , b ) , respectively. The simplified fuzzy number arithmetic operations between the trapezoidal fuzzy numbers A₁ and A₂ are as follows,

Fuzzy numbers addition ®

( a 1 ,a₂,a₃,a₄ ) ф ( b₁,b₂,b₃,b₄ )

= ( a 1 +b 1 ,a₂ + b₂,a₃ +b₃,a₄ +b₄ )

Fuzzy numbers subtraction

m

2 xij - bj for j = 1,2.....,n i=1

Xy - 0     for i=1,2,.,m and j= 1,2,,.,n

Where a_t = ( a_x , a ₂, a ₃, a ₄ ) , b. = ( b_x , b ₂, b ₃, b ₄ ) and Gy = ( c_tj, c^ ., c^ , c ) representing the uncertain supply and demand for the transportation problem.

E

— m

E

( a 1 ,a₂,a₃,a₄ )□ ( b 1 ,b₂,b₃,b₄ )

= ( a 1 -b₄,a₂-b₃,a₃-b₃,a₄-b₁ )

Multiplication used by Stephen Dinegar.D

a.b= [^{a 1} (b +b +b +b ), ^{a 2} (b +b +b +b ), 1234  1234

• ^{a 3} (b₁+b₂+b₃+b₄),^{a 4} (b₁+b₂+b₃+b₄)], 爄 f R(a)>0

a.b= [^{a 4} (b +b +b +b ), ^{a 3} (b +b +b +b ), 1234  1234

• ^{a 2} (b 1 +b 2 +b 3 +b 4 ),^{a 1} (b 1 +b 2 +b 3 +b 4 )],if R(a)<0 44

• 2.8 Ranking Function [17]

Example:

Let A 1 and A 2 be two trapezoidal fuzzy numbers, where

A = (1, 2, 3, 4) and A ₂ = (5, 6, 7, 8) . Then,

A 1 Ф A 2 = (1,2,3,4) Ф (5,6,7,8) =(6,8,10,12)

A ₁ A ₂ = (1,2,3,4)     (5,6,7,8) =( -7,-5,-3,-1)

Many different approaches for the ranking of fuzzy numbers have been proposed in the literature. In this Fuzzy Russell’s method we use Yager’s[17] ranking method. A ranking function R: F(R) ^ R which maps each fuzzy number into the real line, F(R) represents the set of all trapezoidal fuzzy number. If R be any ranking function, r (a) = a1 + a 2 + a3 + a 4

For any two trapezoidal Fuzzy number A = ( a 1 ,a ₂, a ₃, a ₄) and B = ( b 1 , b ₂, b ₃, b ₄) then we have,

• ( i )    A <  B  ^ R ( A ) <  R ( B )

• ( ii )    A - B  ^   R ( A ) - R ( B )

• ( iii )    A = B  ^   R ( A ) = R ( B )

3.1 Algorithm for Fuzzy Russell’s Method

III. The Computational Procedure for Fuzzy Russell’s Method

In this section we proposes modified method called as Fuzzy Russell’s method is used for finding initial basic feasible solution for Fuzzy transportation problem. The solution procedure as follows,

Step 1: Calculate the quantities u _i , v and ij using

ui =

max

1 < j <  n

{Gj }

For i=1, 2,

m

*ij ^} For j=1, 2,n

2.7 Mathematical Formulation of Fuzzy Transportation Problem

Minimize: Z = ^^ c c j x j

Subject to,

n

Ex. < a. for i=1,2,,m ij           i j=1

max

Vi = j    1< i < m and П-. = c.. — u. — V . For all i,j. ij        ij        i         j

Step 2: Select the variables x ( x ij ⁽¹⁾, x ij ⁽²⁾, x ij ⁽³⁾, x ij ⁽⁴⁾) having the most negative value of .If there are ties in the value of      ,Select x ( x ij ⁽¹⁾, x ij ⁽²⁾, x ij ⁽³⁾, x ij ⁽⁴⁾)

with the smallest unit cost c ( c ij ⁽¹⁾, c ij ⁽²⁾ , c ij ⁽³⁾ , c ij ⁽⁴⁾).If there are ties again in the value of c _ij ( c ij ⁽¹⁾, c ij ⁽²⁾, c ij ⁽³⁾, c ij ⁽⁴⁾),select x_ij ( x ij ⁽¹⁾, x ij ⁽²⁾, x ij ⁽³⁾, x ij ⁽⁴⁾) with the largest amount of remaining source supply or destination demand.

Step3: Set the activity level of x ( x _i j ⁽¹⁾, x _i j ⁽²⁾, x _i j ⁽³⁾, x ij ⁽⁴⁾) equal to the smaller value between the source supply a and the destination demand b .

Step4: Subtract x ( xij(1), xij(2), xij(3), xij(4)) from ai and b found in step3. Eliminate from the transportation table the row or column that results in a zero supply or destination demand after this subtraction. Stop if all ai (i = 1, 2,…, m) and b (j = 1, 2,…, n) are zero, otherwise go to step1.

• IV.    Numerical Example

Consider the Fuzzy transportation problem.

Here cost value, supplies and demands are trapezoidal fuzzy number. Here a and b are Fuzzy Supply and Fuzzy Demand. Fuzzy Russell’s method is used to finding the initial basic feasible solution.

D1 D2 D3 D4 ai S1 (1,2,3,4) (1,3,4,6) (9,11,12,14) (5,7,8,11) (1,6,7,12) S2 (0,1,2,4) (-1,0,1,2) (5,6,7,8) (0,1,2,3) (0,1,2,3) S3 (3,5,6,8) (5,8,9,12) (12,15,16,19) (7,9,10,12) (5,10,12,15) bj (5,7,8,10) (-1,5,6,10) (1,3,4,6) (1,2,3,4) (6,17,21,30) mn

Therefore ^ a_t = ^ bj , the problem is balanced i = 1          j = 1

Now we applying the Fuzzy Russell’s method for fuzzy transportation problem we have, fuzzy transportation problem. There exists a fuzzy initial basic feasible solution.

D 1	D 2                       D 3                       D 4                       a i
S 1               (1,2,3,4)	(-5,2,4,11)               (1,3,4,6) (1,3,4,6)                  (9,11,12,14)               (5,7,8,11)                (1,6,7,12)
S 2               (0,1,2,4)	(0,1,2, 3)                   (5,6,7,8)                   (0,1,2,3)                   (0,1,2,3)
(5,7,8,10) S3               (3,5,6,8)	(-15,-1,3,15)                                        (1,2,3,4) (5,8,9,12)                 (12,15,16,19)             (7,9,10,12)                (5,10,12,15)
b j              (5,7,8,10)	(-1,5,6, 10)               (1,3,4, 6)                 (1,2,3,4)                 (6,17,21,30)

Therefore the initial basic feasible solution is,

Minimum Z ( Z(1), Z(2), Z(3), Z(4))

= [(-5,2,4,11 ) (1,3,4,6)] + [(0,1,2,3)(-1,0,1,2)] + [(5,7,8,10) (3,5,6,8)] + [(5, 7 ,8 ,10 ) (3,5,6,8)] +[(-15,-1, 3, 15) (5, 8, 9, 12)] + [(1, 2, 3, 4) (7, 9, 10, 12)].

Minimum Z ( Z(1), Z(2), Z(3), Z(4))

= (158.25, 90.5, 158.25, 328.5)

The crisp value of the Fuzzy Transportation problem is 183.875.

• V.    Conclusion

We proposed Fuzzy Russell’s method to find the initial basic feasible solution using Yager’s ranking method with trapezoidal fuzzy numbers. This method can be used for all kinds of fuzzy numbers. This method is very easy to apply and can be utilized for the fuzzy transportation problem. This technique can also be tried in solving other types of problem like, project schedules, assignment problem and network flow problem.

Acknowledgment

The authors would like to heartily thank the Editor in Chief and anonymous reviewers for their careful reading of this paper and for their helpful comments.