A Modified Parallel Heuristic Graph Matching Approach for Solving Task Assignment Problem in Distributed Processor System

Published Online September 2013 in MECS DOI: 10.5815/ijitcs.2013.10.08

The Task Assignment Problem plays an important role in recent computational systems which involve processing multiple tasks in a multiprocessor environment. The Task Assignment Problem has been proved to be a NP-Hard problem. Several Algorithms and methodologies [1-5] have been proposed to solve the Task Assignment Problem. Most Algorithms use Graph Partitioning and Graph Matching Techniques. Significant research has been carried out in solving the Task Assignment Problem in a parallel environment.

This paper discusses the Shen Tsai’s Algorithm [6] on Task Assignment. Also, a detailed description about the parallel algorithm suggested in the paper “A parallel Heuristic Graph Matching Method for Task Assignment” [7], HGM Algorithm to solve the Task Assignment Problem in a distributed environment is given. The observations made in the above algorithms were analyzed and scope for improvisations has been identified and a new “Parallel Heuristic Graph Matching Algorithm” is proposed to improvise the current techniques. Further, this paper contains a detailed analysis, both qualitative and quantitative, about the algorithm that signifies how efficient the proposed algorithm is, compared to the existing ones.

The proposed algorithm tries to solve the basic Task Assignment Problem of “mapping ‘k’ distinct tasks to ‘p’ different processors” using ‘n’ processor distributed system. An analysis on Shen Tsai’s Algorithm for Task Assignment [6] based on A* Algorithm [8] describes how the sequence of assigning various tasks to the processors in the solution tree formed in the algorithm contributes to the total computation time of deciding the most optimal assignment. Hence, the proposed algorithm tries to identify the optimal sequence of Tasks for assignment to the processors in the solution tree so that the Total Computational Time is optimized. Further, a qualitative analysis on [7] shows how the HGM algorithm deals with the Task Assignment Problem of “mapping ‘k’ distinct tasks to ‘p’ different processors” using ‘n’ processor distributed system where n > p only. But our proposed algorithm is designed to work for all general Task Assignment Problem [9] cases where n>p, n

In the RELATED WORK section a detailed description about Shen Tsai’s paper on Task Assignment based on A* Algorithm and HGM Algorithm of [7] is provided . In the further section a PROBLEM STATEMENT is provided. Later, the actual solution is proposed in the SOLUTION section and the ANALYSIS section provides a detailed qualitative and quantitative analysis on the proposed algorithm and sufficient justification about the efficiency of the proposed algorithm is provided in the EXPERIMENTATION section in the form of mathematical and statistical observations and facts. Finally the CONCLUSION section describes about the conclusions of our propositions and the further scope for improvisations.

• II.    Related Work

• 2.1    Shen Tsai’s Paper on Task Assignment Based on A* Algorithm

Consider the Task Assignment Problem of “mapping ‘k’ distinct tasks to ‘p’ different processors”. Let the tasks and available processors be represented by following Task and Processor sets T and P.

Task Set      - T = {t 1 , t 2, t 3, …, t k }

Processor Set - P = {p 1 , p 2, p 3, …, p p }

According to Shen and Tsai, all tasks can be represented in a single task graph. Each node in the task graph corresponds to a particular task while an edge between 2 tasks corresponds to the communication cost between 2 tasks when processed on 2 different processors [Fig 1]. Similarly all the processors can be represented by a processor graph where the graph represents various interconnections between processors in the actual distributed system [Fig 1].

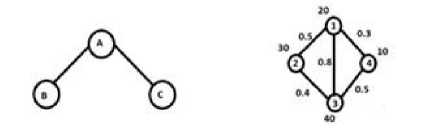
Fig. 1: Processor graph and task graph

Mathematical Formulation:

Let us consider any general mapping M, M: T to P, where T and P correspond to the Task Set and Processor Set respectively.

Let the completion time of a particular mapping M is denoted by Time (M) function.

To calculate Time (M),

• 1)    We need to calculate Time (M, P k ) ,the time of completion for a processor P_k in a given mapping M, for all P_k belongs to P. We need to calculate the time of completion individually for each processor because in any parallel environment the total time for completion

of all tasks is the maximum of the times taken by each processor to solve all the tasks assigned to the processor .

Consider a mapping of Tasks 1, 2, 3, 4, 5 to be mapped to processors p1, p2 as 1 p1, 2 p2, 3 p1, 4 p1, 5 p2.

Then,

Time (M) = Maximum (Time (M , P 1 ), Time (M , P 2 ))

Now Time (M, P k ) is calculated as

^ (T к + ^ communication cost;.,)

^{t i                 t 1}                                                                (1)

Such that “t i and t l belongs to T”, “t i is allocated to P k ” and “t_l belongs to T and t_l is not allocated to P_k”.

Where Ti,k is the computation time for ith task when executed on kth processor.

• 2)    Time (M) = Maximum (Time (M, P_k)) for all P_k belongs to P.

It follows that Time (M) is the maximum of all the times taken by each of the processor.

An optimal mapping ‘M’ corresponds to a mapping where Time (M) is minimum [10].

Solution for Optimal Mapping ‘M’:

The solution is represented as a tree, called as the solution tree built according to the following rule:

“Let {t₁, t_2, t_3, …, t_k} be a permutation of all tasks in task set T. At any level i of the tree only task t_i is assigned to all processors. Each node in the solution tree has (tasks, processors) as its attributes. So in building the solution tree we start with a dummy root node (level zero) and proceed with level 1 by assigning Task t 1 to all processors and get the initial nodes. From here we calculate ‘f’ value for each node in level1 and expand the node with least ‘f’ value.”

After expanding a node, we then scan through the entire tree for minimum ‘f’ value and go expanding about it. This is continued until we end up in a goal state such that all tasks are assigned to a processor.”

Calculation of ‘f’ value is done in a heuristic fashion:

The value of f is calculated as

fn = gn + hn                                (2)

Where g n is the computation time involved for reaching a particular node ‘n’ from start node and h n is the Heuristic approximate for present node to reach final goal state.

Calculation of the heuristic part (h) of the ‘f’ value is an interesting topic of research and many techniques have been proposed to find the heuristic. It is assumed that the heuristic is obtained from one of the existing algorithms [7].

Observations:

The efficiency of Shen Tsai’s Algorithm is determined by the number of nodes generated in the solution tree. Our analysis proves that the number of nodes generated depends on the permutation of T i.e. the sequence in which we assign the tasks to the processors in the solution tree reflects the number of nodes generated in the solution tree.

i.e., The Permutations

T1= {t 1 , t 2, t 3, …, t n },

T2= {t n , t n-1, t n-2, …, t 1 },

All of the above permutations generate a different number of nodes in the solution tree thereby resulting in different computational times to get the optimal assignment.

“Hence, finding the optimal permutation, i.e. the permutation which results in the most optimal solution is an interesting point of research.”

• 2.2    HGM Algorithm for Task Assignment Proposed in[7]:

This paper discuss about parallelizing the Shen Tsai’s Algorithm to solve the Task Assignment Problem [9] of “mapping ‘k’ distinct tasks to ‘p’ different processors” in an n processor distributed system.

The algorithm works as follows:

Assumptions:

“The number of processors available in the distributed system to solve the task assignment problem is greater than or equal to the number of processors involved in the task assignment problem.”

Algorithm:

• (i)    Initially consider the Task Assignment Problem of mapping “k tasks to n different processors” to be solved on an ‘n’ processor distributed system.

• (ii)    Each processor in the Task Assignment Problem is assigned to a single processor in the distributed system. If processor A of the problem is assigned to processor 1 in the distributed system, then Processor 1 can assign tasks only to Processor A.

• (iii)    The processors in the distributed system start assigning tasks to the processors in the problem until a fixed interval (3 or 4 tasks) after which the ‘f’ value is calculated for the assignment in each of the processor in the distributed system.

• (iv)    All the processors in the distributed system communicate and interchange the f values to decide the optimal assignment. Once the optimal assignment is

decided all the processors proceed with assigning the tasks about this optimal assignment.

• (v)    Steps (iii) and (iv) are repeated until all the tasks are assigned and an optimal mapping is achieved.

The Algorithm is best explained by the following example:

Consider “2 processors and 5 tasks “TASK ASSIGNMENT problem. We a have 2 distributed processors to solve this problem. Let us assign processor A to processor 1 and processor B to processor 2. Hence processor 1 will only assign tasks to A processor and processor 2 will assign tasks to B processor. Now,

PtOtOSSOr 1                   Protestor 2

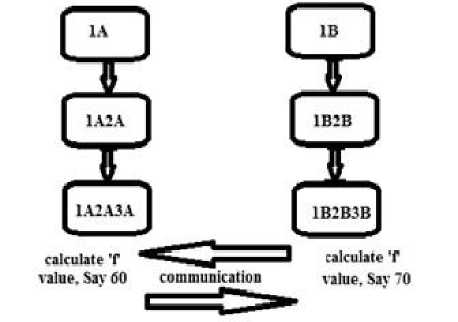
Fig. 2: First Cycle of Execution

Protestor 1                  Protestor 2

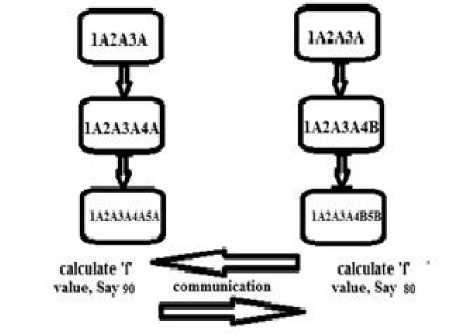
Fig. 3: Second Cycle of Execution

Hence the optimal assignment is 1A2A3A4B5B

Observations

We observe that the above parallel algorithm can be extended to the following cases only:

• (i)    “n tasks- p processors” Task Assignment Problem and you have p processors to solve the Task assignment problem

(Or)

• (ii)    “n tasks- p processors” Task Assignment Problem and you have greater than p distributed processors to solve the task assignment problem

“Hence, finding the parallel algorithm which works for solving all general Task Assignment Problems of “mapping ʻkʼ distinct tasks to ʻpʼ different processors” in n processor distributed system where n>p, n

• III.    Problem Statement

To develop a modified parallel heuristic task assignment algorithm which:

• 1.    Identifies the ideal permutation of tasks that results in the least computational time to find the most optimal assignment, and

• 2.    Extends the parallel HGM Algorithm to run for any number of Generic Processors in the Distributed System.

• IV.    Solution4.1    identify the ideal permutation:

Consider Tasks - T = {t 1 , t 2, t 3, …, t k }

Processors - P = {p 1 , p 2, p 3, …, p p }

It is needed to map ‘k’ Tasks to ‘p’ processors. Now to obtain the solution tree, we should decide on the optimal permutation,

п = {Y, Y2, Y„..., Yk}

Such that π is a permutation of T = {t 1 , t 2, t 3, …, t k }.

The sequence of the tasks is significant (as discussed) because in the solution tree only the kth task in permutation is mapped to all processors in the kth level of the solution tree.

Now the various ways of choosing the permutation are:

• a)    Based On Computation Time

We should choose a permutation,

п = {Y1, Y2, Y.,..., Yk }

Such that,

Mean computation time (Y j ) > Mean computation time (Y j+1 )

i.e., т д-T д-...д-T Т + Т   +--- + Г

Tj,1 + Tj,2 +    + Tj,p > Tj+1,1 + Tj+1,2 +    + Tj+1,p pp  (4)

where, T j,i refers to the cost of processing when Y j is executed on Processor ‘I’

• b)    Based On Communication Cost

We should choose a permutation,

п = {Y1, Y2, Y.,.., Yk }

Such that

Total communication time   (Yj)   > Total communication time (Yj+1)

i.e.,

CC[ j ] > CC[( j +1)]

Where CC [j] corresponds to the summation of all the communication costs of Task Y j with all other tasks which do not run in the same processor as that of Y j _.

The 1st way of choosing the permutation is useful if the computation costs of tasks are more significant than the inter task communication costs. While the 2nd way is better in cases where the inter task communication cost is greater than the computation cost of tasks.

This paper proposes an alternate way which takes care of all average cases where both computation cost and communication cost are equally significant.

At this stage, a quantity referred to as ‘α’ is defined for each task which proves helpful in deciding the most optimal permutation. α is defined for any particular task, t j as

• OY ,) = {j+^j^ + CC[jl pk

• 4.2    m odified hgm a lgorithm :

Now a permutation of T is chosen, ^п = {^{Y1 , Y 2, Y} з ^,...^{, Y} n ^} ,suchthat a (Y j) > a (Y j + 1 )

Hence, the ideal permutation which gives an optimal assignment in the most optimal time is found.

Consider the Task Assignment Problem of “mapping ‘k’ distinct tasks to ‘p’ different processors” in an n processor distributed system [11].

Algorithm

Step1: Distribute the “p processors” of the problem into ‘n’ processors.

Step2: Any processor in the distributed system can assign the tasks only to those which are assigned to it.

• I .e. if processors A, B, C are assigned to Processor1 in the distributed system, Processor1 can assign tasks only to A, B and C.

Step3: Now in each of the processor 1, 2, 3 . . .N of the distributed system a solution tree is built individually, containing only the assignments to the processors which are assigned to this particular processor up to 3 levels, break and find the best node space from each solution tree based on the ‘f’ value.

Step4:   Each of the distributed processors communicates to decide on the ideal state space and start expanding about it.

Step5: Step3 and Step4 are repeated until all the tasks are assigned to the processors and an optimal assignment is obtained.

Example:

An example illustrates the above algorithm. Consider,

• V. Analysis

• i)    The efficiency of the first part of the algorithm to find the most optimal task permutation is very much obvious and evident. It is well supported by the experimental data represented in the next section.

• ii)    The parallel part of the algorithm is very efficient because:

• c)    In a general problem of k tasks- p processors Task problem to be solved using ‘n’ processors, the proposed algorithm will work for all:

• (i)    p> n

• (ii)    p=n

• (iii)    p

(Though it is highly efficient in case of p>n.)

• d)    This algorithm uses Shen Tsai’s algorithm to the fullest by implementing it in finding intermediate ideal state spaces in each of the distributed processors unlike the HGM algorithm which uses a brute force approach and simple heuristic based on A* Algorithm to find intermediate ideal state spaces.

Task Set, T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} Processor Set, P = {A, B, C, D, E, F}

Let p1, p2, p3 be the Processors in the distributed System to solve the Task Assignment problem

Then, the following figure represents the state spaces after 3 allocations based on above algorithm in the 3 processors of the distributed system,

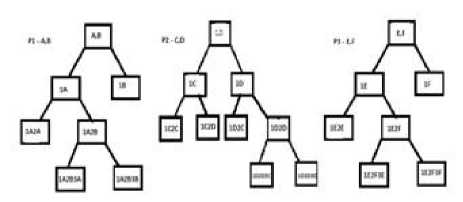
Fig. 4: Execution of the Algorithm in all Processors

Say at the end of 3rd level fp1, fp2 and fp3 correspond to the ideal f values from Processors P1, P2 and P3 respectively, amongst which fp2 has the least ‘f’ value.

Let us say fp2 corresponds to the node 1D2D3C in P2’s solution tree. Now, all 3 processors p1, p2, and p3 start expanding about 1D 2C 3D state space. This process is repeated until a goal state where all the tasks are assigned to processors is achieved.

• VI. Experimentation

A test case is represented in figure below. The figure represents a task graph with vertices pointing to tasks and the edges pointing to inter task communication cost when processed on different processors.

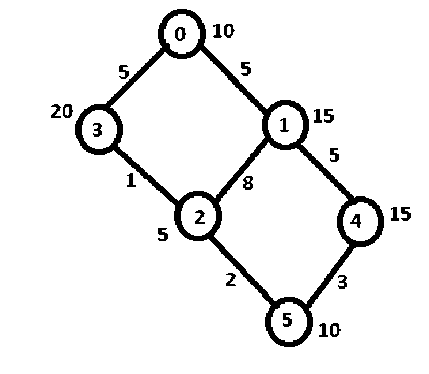
Fig. 5: Task Graph – Test Case

In Figure 5, the number of nodes in the task graph is 6, which means that there are 6 tasks defined by T = {0, 1, 2, 3….5} which need to be mapped. The computation time associated with these tasks is defined by the set TP = {10.0, 15.0, 5.0, 20.0, 15.0 and 10.0}. The inter task communication is defined by the matrix C .

C is given as under

Let us assume the above tasks should be mapped on to 2 processors.

e) To test the efficiency of the first part of the algorithm which identifies the optimal permutation

A Task Assignment is made first using the regular Shen Tsai’s Algorithm. Later task assignment is done using the most optimal assignment .

An index called the optimality index denoted by ‘ σ ’ is introduced as,

Optimal Turnaround Time in the proposed Algorithm Optimal Turnaround Time in Shen Tsai's Algorithm

Similarly an index, ‘ θ ’ is defined as,

Number of Nodes Generated in proposed Algorithm θ=

Number of Nodes Generated in Shen Tsai's Algorithm

The results are expressed in the following Table 1,

Table 1: Results Comparing Proposed Algorithm and Shen Tsai’s Algorithm

Optimal Mapping	Turnaround Time In Shen Tsai’s Algorithm	Turnaround Time In Proposed Algorithm	No. Of Nodes Generated In Shen Tsai’s Algorithm	No. Of Nodes Generated In Proposed Algorithm	σ	θ
0A1B2B3A4B5A	42.09	41.8	32	12	0.993	0.375

The indices σ and θ represent time comparison factor and space comparison factor of both the algorithms. We observe that both σ and θ fall below 1 signifying the superiority of proposed algorithm over the Shen Tsai’s Algorithm. It is observed that though the change in time complexity is less significant, the change in space complexity is very significant and appreciable.

• f) To test the efficiency of the parallel part of the proposed algorithm

Now, let us consider the following two scenarios

Scenario 1: The above task problem is solved in a parallel way with HGM Algorithm using 4 processors.

Scenario 2: We solve the above task problem in a parallel way using the proposed parallel algorithm with 2 processors.

Let σ and θ be redefined to this context as follows,

Effective Turnaround Time in the proposed Algorithm

Effective Turnaround Time in HGM Algorithm      (9)

Where, Effective Turnaround time is defined as Optimal Turnaround Time per processor used in the distributed system

Similarly,’ θ ’ is defined as,

Number of Nodes Generated in proposed Algorithm θ =

Number of Nodes Generated in HGM Algorithm

The results are expressed in the following Table 2,

Table 2: Results Comparing Proposed Algorithm and HGM Algorithm

Optimal Mapping	Turnaround Time In HGM Algorithm	Turnaround Time In Proposed Algorithm	No. Of Nodes Generated In HGM Algorithm	No. Of Nodes Generated In Proposed Algorithm	σ	θ
0A1B2B3A4B5A	21.2	16.38	24	19	0.77	0.79

It is observed that both σ and θ fall below 1 signifying the superiority of proposed algorithm over the HGM algorithm proposed in the research paper [7]. A very significant change in both time complexity and space complexity is observed experimentally thereby establishing the efficiency of the proposed algorithm. It should also be noted that only half the number of processors were used in the distributed system to solve the task assignment problem. Still the algorithm works efficient when compared to the traditional HGM algorithm.

• VII.    Conclusion

This paper establishes a methodology to parallelize the Heuristic Graph Matching Algorithm proposed by Shen Tsai, which can be solved with the help of any generic distributed system containing any number of processors. Further the paper provides an approach to minimize the number of nodes generated in the solution tree developed to obtain the Optimal Task Assignment Mapping in the Shen Tsai’s Algorithm. Due to parallelizing and proceeding with an optimum Permutation of tasks the number of state spaces generated is reduced significantly and hence the complexity reduces. The proposed Parallel Algorithm follows a divide and conquer approach to solve the discussed Task-Assignment Problem.

• VIII.    Further Research

The following areas are identified for further research:

• 1.    To investigate the algorithm for larger test cases

• 2.    To identify the ideal permutation based on other properties specific to the Task Assignment Problem.

• 3.    To devise an algorithm for heterogeneous processor systems.