A Modified T-S Model Fuzzy Adaptive Control System Based on Genetic Algorithm

Published Online June 2011 in MECS

Rapid growth of industries has not only enhanced the productivity but also resulted in the production and release of toxic substances into the environment, creating health hazards and affected normal operations, flora and fauna. Wastewater treatment is one of the most significant measures for protecting environment. For this end, bioengineered technologies adapted for each type of organic and toxic wastes are required to achieve high treatment efficiencies at low capital costs.

Fluidized bed bioreactor has several advantages over other conventional reactors for the treatment of wastewater[1]. During the past few years the application of fluidization has increased considerably in the field of chemical, biochemical engineering and in wastewater treatment. In which the three-phase Fluidized Bed Bioreactor (FBBR) is becoming one of the research hotspots in the wastewater treatment industry due to its characteristics of high efficiency, small occupation area, wide adaptability and strong load capacity[2]. However, it is difficult to modeling and control the bioreactor

process because of its characteristic of long time-delays. The process of wastewater treatment is a rather complex biochemical reaction procedure that needs a long time period for building its biological and chemical process balance. As an extraordinary instructional parameter in the biochemical reaction process, dissolved oxygen(DO) could reflect directly and readily the operational state of the whole system[3]. If the concentration of dissolved oxygen is low, treated water quality will fail to meet standard, otherwise it will cause energy waste. Consequently, an effective measurement for dissolved oxygen can indirectly improve the treated water quality of wastewater treatment and can retrench the system energy consumption. In the wastewater treatment system, most of the control methods adopt regular fuzzy control or traditional PID control at present[4]. Although regular fuzzy control could actualize rapidity and stability of transience response, it’s difficult to eliminate steady-state error. On the other hand, PID control is simple, but it cannot set parameter online, at the same time with deficiency both in dynamic and static performance [5][6]. Moreover, neither PID control nor regular fuzzy control can surmount the influences cause by long time-delays of system.

In addition, FBBR system is a time-varying control object with multi operating condition, the fixed control parameters can not be applicable to the whole process. In this case, self-adaptive control system is very necessary. By measuring the different states or a variety of performance parameters continually, the self-adaptive control system can get the differences between the actual measured values and the expectations, consequently to adjust the control parameters and its structure, finally make the control system operate in the optimal or sub-optimal state[7]. These properties of adaptive control can guarantee the water quality meet the requirement, for the wastewater treatment system based on FBBR in the case of the input water quality fluctuations.

This paper presents a modified T-S model fuzzy adaptive control method based on genetic algorithm (GA), Using GA to optimize the membership function of the T-S fuzzy controller, ensure effluent quality stable in the case of influent water quality changing for the wastewater treatment system, furthermore, introduce the fuzzy predictive compensation module to resolve the time-delay issues in the wastewater process and correct the feedback of system (BOD value), thus ultimately realize the optimal control for the wastewater treatment system based on FBBR.

This paper is organized as follows. In the following section we describe the FBBR experimental equipment and control system model. In section 3, a modified fuzzy adaptive control system based on T-S model is presented. In section 4 make the experiments and analyze the results, finally in last section get the conclusion.

• II.    FBBR Experimental Equipment and Control System model

A.FBBR Experimental Equipment

The configuration of FBBR wastewater treatment system is shown in Fig.1

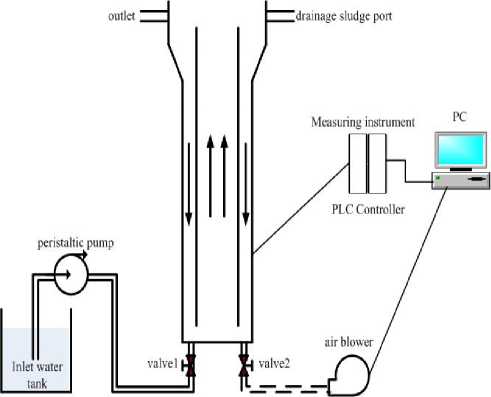
Figure 1. The configuration of FBBR experimental equipment

In the process of FBBR wastewater treatment, high level monitoring computer is responsible for dealing with the information of parameters. The computer, operated by PLC control converter, adopts compound control algorithm to generate control maneuvers for dissolved oxygen, and further regulate rotational speed of blower. In order to supplement the dissolved oxygen in the aeration tank and to accomplish the whole control process, the air in the blower is transfused into aerobic tank through intake pipe connected with aeration tank.

B. Control System Model

The control system is a closed-loop system, which

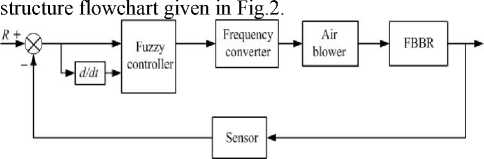
Figure 2.the structure flowchart of control system

First, the setting value and test value of DO is compared, and then the result is the input of fuzzy controller, to generate control strategy, which can regulate the rotating speed of blower and thereby control the aeration volume and the DO value of FBBR.

The FBBR can approximately be seen as a first-order inertial element with delay[8], which the transfer function is

G i (s ) = e ^{-T s} /( Ts +1)                (1)

where т is the delay time constant, and T is time constant. The mathematical model of converter and blower is equivalent to [9]

G 2 ( s ) = K /(T m S + 1)              (2)

where K is transfer coefficient, T is time constant, m according to the engaging performance parameter of blower, the transfer function can be computed as

G ₂( s ) = 1/(100 s + 1)                (3)

The system can converted into unit feedback system through using the check-transmit unit of feedback loop as gain K.

• III.    The Modified Fuzzy Adaptive Control Systm Base on T-S Model

• A. The Design of T-S Fuzzy Controller

T-S model is a typical fuzzy control model proposed by Takagi and Sugeno[10], which widely used in the system identification and control. The rules based on T-S model are expressed as follows:

• R: IF x ₁ is A ₁ , x ₂ is A ₂ , …, x_n is A_n

THEN y = b0 + b1 x1 + b2x2 + ■ + bnxn (4) where, x (i = 1,•••,n ) is the input variable at time i ; Ai (i = 1,•••,n ) is fuzzy sets describing the variable xi, the parameters of the membership function referred to as the premise parameters, y denotes the output of fuzzy control model, bk (k = 0, ■, n)

As the T-S model have a certain degree of structural similarity with the regular PID controller, and the rules consequent of T-S model adopted a precise linear set similar to the PID algorithm, so it is feasible to realize the PID control by using fuzzy controller based on T-S model.

We select the system error e , error rate ec = j e and accumulation error es = e as the variables of the rules in

(4), and let b ₀ = 0, then the output u as follows:

u = b 1 e + b ₂ j e + b ₃ e                (5)

Assumed there are N rules in the systems, and using algebraic integral – centre of gravity fuzzy reasoning method, then the output u_i of fuzzy PID controller which based on T-S model as follows:

NNN

i=1                     i=1

N

Where, k ' = w i / ^ w i is the relative weight coefficient, i =1

while w' = ^Ai(e)MBi (j e)^Ci (e) is the weight coefficient. Comparing (6) with the conventional PID controller, can get the three parameters of fuzzy PID controller based on T-S model which corresponding to the PID controller:

N

K f - P = Z kb

• ■=1

N

К - 1 = £ kb 2            (7)

i =1

"

K f - D = Z kb i =i

Then, (6) can be expressed as:

u = K f - p e + K f - 1 J e + K f - _De         (8)

From the above analysis, we can get the T-S fuzzy controller compared with conventional PID controller is a PID controller with generalized parameters. KP , KI KD is constant or piecewise constant in the general PID controller, while K , K K is variable in the T-S F - P    F -1    F - D fuzzy controller. According to (8) and fuzzy rules, we can find that K , K , K is associated with error,

F - P , F -1 , F - D                                         , accumulation error and error rate respectively, therefore, T-S fuzzy controller can be seen as a PID controller with variant parameters. As the membership function is nonlinear, so that controller is also a non-linear PID controller, this is the T-S fuzzy controller with multi-rules is the composite of several general PID controllers, in some different cases, the final output is obtained by the combined effect of the PID controller determined by single rule and the different weighting factors.

• B.    the Mod f ed T-S Fuzzy Adapt ve Controller Based on GA

The structure of general T-S fuzzy controller is simple and be apt to realize in engineering project. It can approximate any nonlinear function with high-precision in theory. However, there are still the following questions in practice because of the time-varying characteristics of the wastewater treatment process:

• •    All the membership functions are linear functions and don’t have the self-adaptability and flexibility;

• •    Impossible to achieve the parameters selection optimally.

For the actual model, the ability to choose the optimal membership function and its parameters will directly affect the T-S model have better self-adaptability, as well as the approximation validity with any accuracy. In order to solve the problem, we present an optimization approach based on genetic algorithm for system parameters.

• •    All of the membership functions in control system are using the generalized Gaussian membership function with self-adaptive variable parameters;

• •    Using genetic algorithm to search the optimal solution of the self-adaptive parameters in the generalized Gaussian membership functions.

In the practical application of fuzzy control, the membership function of fuzzy set usually is triangular, trapezoid, Gaussian or other exponent. The feature of these membership functions is that once the type is given then the general shape can not be changed. Meanwhile, the generalized Gaussian membership function with self-adaptive which can adjust parameters to approximate triangular, trapezoid or other exponent functions is prone to solve the nonlinear, time-delay, time-varying problems, and ultimately meet the system performance requirements.

As concerned as above, we select a class of generalized Gaussian membership function:

M f ( X ) = exp( -

x - b

a

c

)

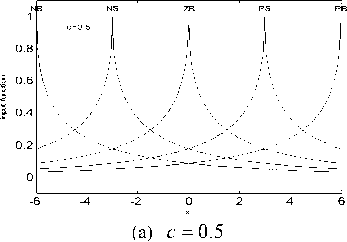
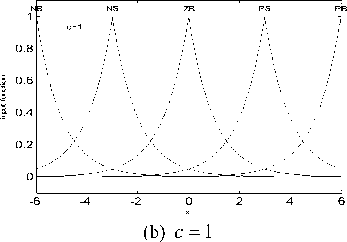
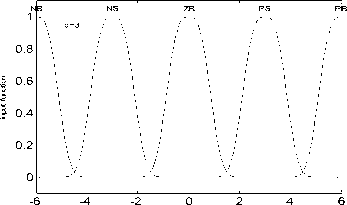
Where, a >  0, b e R , c > 0 . When a = 1 , b = 0 and c were 0.5, 1, 3, 5 respectively, the curves of the generalized membership functions are shown in Fig. 3.

x

^(c) c = 3

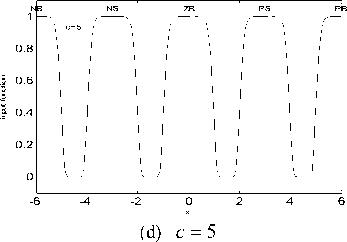
Figure 3 ． Curves of generalized Gaussian membership function with different c values

As shown in Fig. 3, the generalized membership function can be translation, compressed or expanded by choosing different c values, thereby can approach triangle, trapezoid, Gaussian or other functions. It can be seen that this kind of generalized Gaussian membership function have self-adaptive.

In summary, the modified T-S fuzzy adaptive control method based on GA proposed in this paper is search the relevant global optimization parameters of generalized membership function, thus changing the membership function. In order to obtain a satisfactory dynamic performance, this paper select the weighted factor which is compose of absolute error e( ( i )| = f ( c ( i )) and error rate

|ec ( i )| = f ( c ( i )) as a objective function for optimizing the parameters of the membership function.

J ( i ) = a ^ e ( i )| + в \ ec ( i )|            (10)

Where, e denotes the error of FBBR control system, and ec denotes the error rate.

To avoid overshoot, the punishment mechanism is adopted, that is, the overshoot is set to be one term of target function in case of it happened. Thus, the optimal performance is set as follows:

J ( i ) = a ^ e ( i )| + вec ( i )|      e ( i ) ^ 0

J ( i ) = J ( i ) +100 e ( i )          e ( i ) < 0

After repeated test and verify, we set a = 0.9, в = 0.1.

The initialize value of individuals is 100, the evolutionary generations is 10, crossover probability P c = 0.9, and adaptive mutation probability P m = 0.2 - [ 1:1 size ] * 0.01 size . Moreover, in order to improve the real-time and stability of control, when the performance is greater than a predetermined threshold, then using genetic algorithm to optimize the parameters of generalized Gaussian membership function; and if the performance is less than the threshold, then don’t need. The algorithm is as follows:

• •    Determine the range of parameters c of generalized Gaussian membership function, there, c e [0.5,9];

• •    Randomly generated 100 individuals to set as initial population P ;

• •    Solve the cost function J and the fitness function f which corresponding to the population parameters;

• •    Perform reproduction, crossover and mutation operation for the population to produce the next generation;

• •    Repeat steps 3) and 4) until parameters convergence or reach the target.

According to the literature [11], we design an integral separation fuzzy controller for reducing the dimension of the controller and decreasing the complexity of fuzzy rules. As shown in Fig.4, where, set the error e and error rate ec as the input of fuzzy controller, and u is the output, then form a two-dimensional fuzzy controller. In Fig.5, the final output U of fuzzy control system is the output of fuzzy controller with the function of integral.

U = u + u se                  (12)

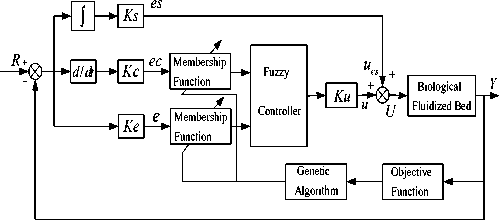
Figure 4. Diagram of modified T-S model fuzzy adaptive control system

• C.    Fuzzy Predictive Control Module

In generally, the wastewater treatment process based on FBBR has large time-delay. Conventional solution is to use Smith predictor method. However, this method had to be known the accurately model of the object, for this case, it is often very difficult to establish the precise mathematical model. Mechanism model are usually obtained under ideal conditions and ignore many factors, so it results large difference with the actual. In order to overcome these shortcomings, we introduce the fuzzy predictive compensation module into the control system discussed previously, and then can achieve good control effect under the condition of without precise mathematical models.

According to the basic principles of Smith’s predictive control[12], the equivalence principle as shown in Fig. 5.

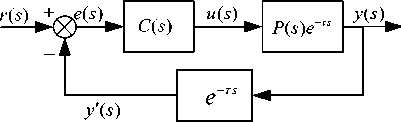
Figure 5. Diagram of Smith equivalence principle

From Fig.5 we can find that the system has a advanced feedback, in accordance with the output y(s) of the object to estimate the delay time т , then compare the system output y'(s) with the given r(s), at last, set the deviation e(s) as the controller input. As the role of delay element, y(t) is the corresponding output for the input at time t - т , and therefore the output y(t) at time t has a linear relationship with the input u (t - т) at time t - т .it can be proved that the total input increment would be expressed as follows[13], which produced in the effect of input at time n before.

n

A y ( t + т ) = y ( t + т ) - y ( t ) » K p T [ K £ u ( t - iT ) - ny ( t )] (13)

i = 1

where, set

n u1 = K^u (t - iT)

i =1

. u 2 = ny ⁽ t )

then there is a approximate linear function between Ay(t+т) and u1 , u2. Therefore u1 and u2 can be set as the conditions of fuzzy controller input, while Ay(t+т)

as the output of fuzzy controller, which constitute a two-input single-output fuzzy relations. The fuzzy rules summarized by the experiments as shown in Tab.1. Tab.1 Fuzzy prediction rules
A У		u 1
		S	M	B
u 2	S	S	M	B
	M	M	S	M
	B	B	M	S

The predictive system makes use of the error compensation to control object. Error compensation e * is calculated by predictive incremental A y (t+ r ) and actual system error based on (11).

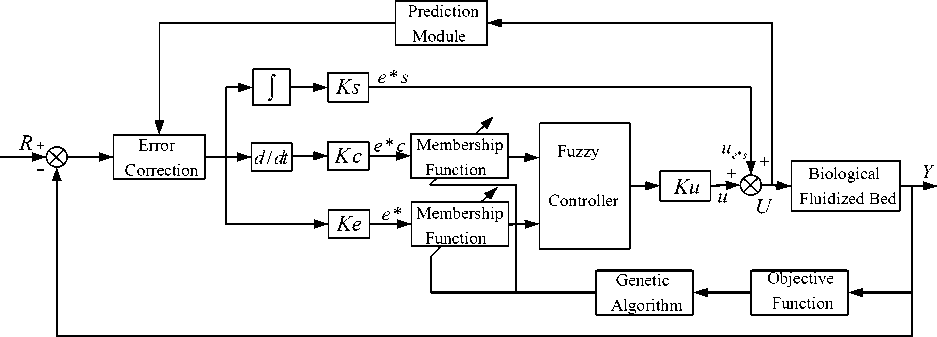
Figure 6. Diagram of wastewater treatment system based on FBBR

• IV. Experimental Results and Analysis

The MSG effluent is treated in an aerobic environment using three phase fluidized bed bioreactor. Experimental setup is shown in Fig.7

Figure 7. Experimental setup

e * = (1 - a ) E e + a E A y ( t + r ) (15) where, a is weights coefficient for the error, the greater its value, the greater proportion in error compensation A y ( t + r ) , that is the greater role of predictive incremental in the control system. Finally, set the actual error rate e * c and the compensation error e * as the fuzzy controller input, resulting in controller output u . The complete block diagram of wastewater treatment system based on FBBR is shown in Fig. 6.

The control model of FBBR wastewater treatment system is double input and single output. The input parameter are e and ec, present the error of dissolved oxygen and the rate of change of error of DO respectively. The output parameter is u, which is the frequency of blower.

The fluidizing column is made up of acrylic which is of 2200mm height, 60mm inner diameter and 70mm outer diameter. Air is sparged using an air blower and flow rate is controlled by flow meter which is of range 0.2-2 lit/min. similarly the effluent is fed into the column and the liquid flow rate is controlled by using peristaltic pump. The effluent is measured by WTW TresCon NH 4 -N Sensor, which range is (10.0-100)mg/L.

According to the actual react process of FBBR system, we select the second-order inertial object control model with pure time-delay element:

G ( 5 ) =---- ^a ^ y E e ~^{r s}         (12)

p      (1 + T p s )²

According to identified with experimental data, where, time constant T p = 30 , delay time constant r = 10 , a = 12 . In this wastewater treatment system based on FBBR, set the measured water quality performance-BOD value and the compensation error e * and error rate e * c as the T-S fuzzy controller input, while blower frequency as the output of fuzzy controller, the design as follows:

The fuzzy sets and domain of the compensation error e * and the error rate e * c defined as follows:

Fuzzy sets of e * : (NB, NS, ZR, PS, PB);

Domain of e * : (-6, +6);

Fuzzy sets of e * c : (N, Z, P);

Domain of e * c : (-6, +6).

Using the generalized Gaussian function as membership function, and applying genetic algorithm to adjust its parameters adaptively.

According to the selected input parameters, the control rules of fuzzy controller based on T-S model is expressed by (4). According to the PID parameter tuning methods combined with expert experience, the following fuzzy rules can be defined as Tab.2.

Simulation results were shown in Fig.8 and Fig.9. From the figures, we can find that regular PID control has larger overshoot when the time constant is changed, the overshoot amount of general PID control is about 20%, reaching stability at 100s; and for the conventional T-S fuzzy control, the overshoot is about 3%, and stability is

Tab.2 Fuzzy control rules

u e ec NB NS ZR PS PB NB 1.1 KPe +1.2 KDec 0.8 KPe + 0.8 KDec KPe+KDec 0.8 KPe + 0.8 KDec 1.1 KPe +1.2 KDec ZR 1.2KPe 0.75KPe 0 0.75KPe 1.2KPe PB 1.5 KPe +1.2 KDec 0.8 KPe + 0.8 KDec KPe+KDec 0.8 KPe + 0.8 KDec 1.5 KPe +1.2 KDec reached at 95s; while for modified T-S fuzzy adaptive control based on GA, the overshoot is less than 3%, and will get stable at 90s. When operation conditions changed, the conventional T-S fuzzy control, can not fit to the conditions changes, and the overshoot become significantly large (about 10%), and control effect is get worse; general PID and modified T-S fuzzy control can be adapted to work well in status changes, the overshoot is still maintained at 19% and 3%, and the modified T-S fuzzy control is superior to general PID control. Simulation results as shown in Tab.3.

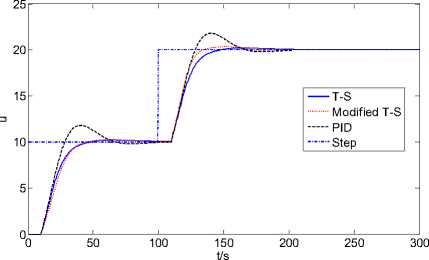
Figure 8. Simulation results of the PID/T-S/Modified T-S method

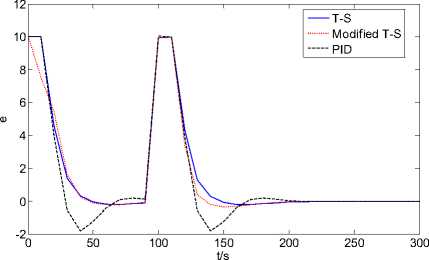
Figure 9. Error of the PID/T-S/Modified T-S method

Compared to general PID and conventional T-S fuzzy control, the modified T-S fuzzy adaptive control based on GA has the characteristics of small overshoot amount and shorter response time, so we can find that the control algorithm proposed in this paper have improved than general PID control and conventional T-S fuzzy control in the performance. It is suitable for DO control of FBBR wastewater treatment system

Tab.3 Simulation results of performance parameters

	General PID	Conventional T-S	Modified T-S
Overshoot (before condition change)	20%	3%	<3%
Response time (before condition change)	100s	95s	90s
Overshoot (after condition change)	19%	5%	<3%
Response time (after condition change)	105s	95s	95s

• IV. Conclusions

For the non-linear, time-delay, time-varying features of the wastewater treatment process based on FBBR, this paper presents a modified T-S fuzzy adaptive control method based on GA. Using genetic algorithms to adjust membership function online to adapt wastewater treatment process in different conditions and introducing a predictive fuzzy model to compensate the feedback error. At result overcome the problem of large time-delay in the wastewater treatment process. As concerned as above, the control method proposed in this paper has the following characteristics:

• •    The controller can perform the nonlinear, complex system without requiring mathematical model;

• •    The fuzzy rules integrate with the experience of experts;

• •    The introduction of integral separation can reduce the complexity and the difficulty of parameter tuning in the fuzzy controller, and easy to implement;

• •    The membership function parameters can be adjusted on-line according to objective function or different operating conditions;

• •    Amend the feedback error by the predictive fuzzy module.

Simulation results show that the control method has better performance than the conventional fuzzy controller, and it can be used as a reference method for practical applications.

Acknowledgment

The authors wish to express their gratitude for the support extended by the authorities of BTBU in carrying out the research work. We would like to thank all the members of the research group for their fruitful insights and commentary. A special thanks goes to Prof. Wang for discussions and help, and Prof. Feng for providing the data.