A Multi-objective Mathematical Model for Job Scheduling on Parallel Machines Using NSGA-II

Published Online August 2016 in MECS

In the industrialized world today due to the decrease of production, depreciation of machinery and equipment manufacturing, energy shortages and increased costs of implementing the required production machinery and equipment, the need to optimize the use of resources and time in the industry is increasingly growing. Scheduling is one the most important topics which has raised the interest of the researchers in industrial and engineering fields. Effective and efficient planning for sequencing production is directly related to increasing the efficiency of production facilities. Scheduling problem because of its use in industry and services has great economic importance and its nonlinear nature, increases its scientific importance. So check solutions to this issue in many fields, including industrial engineering and computer science are common.

Job scheduling problem is obtaining a reasonable timetable in which certain operations assigned to particular machines, at acceptable period of time so that the technological limitations have also been respected. The sequence of the jobs on the machines has a significant impact on the volume of work in process, in a timely manner to meet customer demand and the overall cost of the product. Therefore, in the manufacturing and service-delivery systems, we try to schedule operations in a way that the maximum performance of existing resources, such as labor or machinery is achieved. Simply, the objective is determining the job processing sequence so that the total completion time of all the jobs is minimized.

• •    Each job is made up of several activities. To complete a job, it is necessary to perform all of its activities. The number of job activities is different.

• •    Each activity can be processed only by one

machine at a specific time.

• •    A relation between the activities of a job is a

prerequisite. So if the prerequisite actions are not completed current activity cannot be started. Relations between jobs are not the prerequisite.

• •    The number of available machines is fixed. At any moment machine can only do one activity.

• •    The machines cannot be stopped during execution of a current activity (process) and start it again. A processing machine cannot transfer its current activity to another machine.

• •    There is no need to perform all the activities of a job done by a specific machine, so that even a machine may not be involved in executing any task.

• •    When an activity of a job is finished and the machine is ready for processing the next activity of the same job, the machine is bound to the implementation of new activity during the corresponding preparation time. Time to prepare for the first activity of each job is considered zero.

• •    The machines (and also jobs) are assumed to be as different types (machines are not homo-gen). The machines can take responsibility for processing activities, only for the jobs of the same type.

• •    There is a priority relation among the activities of a job. The jobs are not prior to each other. There is not any priority between activities of different jobs.

• •    The processing cost of each activity on a machine

is also considered.

Considering the above assumptions, the main goal of the proposed model in this paper is optimizing the following objective functions:

• •    Minimizing the maximum total make-span.

• •    Minimizing total machines’ costs.

The remainder of this paper is organized as follows: The literature review and previous works are discussed in section 2. The proposed mathematical model is given in section 3. Section 4 presents the proposed Genetic Algorithm (GA) using NSGAII approach; implementation and the computational results are discussed in Section 5. Conclusion and future work are given in the final section.

• II.    Related Works

The parallel machine scheduling problem has many applications in real environments and it has raised the researchers’ interest during the past years. Due to the NP-hard nature of the problem [1], most of the past works have developed a meta-heuristic approach and have obtained acceptable or better solutions.

Seraj, Tavakkoli-Moghaddam and Julai [2] used mixed integer programming method for open-shop scheduling problem to minimize the average lateness and earliness by a multi-objective fuzzy decision making approach. They also used Taboo search for medium and large scale problems and compared the results with Lingo software. Kacem, Hammadi and Borne [3] developed new methods for flexible job shop scheduling problem consisting localization and Genetic Algorithm. They used new encoding schemes for chromosomes representation used in GA.

Naderi, Zandieh and Fatemi-Ghomi [4] proposed two general techniques which were applicable for scheduling problems too. They used these techniques for job shop scheduling problem considering sequence dependencies. The objective function was defined as total make-span of all the jobs. In this research, four heuristic methods were developed based on GA and Simulated Annealing (SA). Calhoun, Dekcro, Moore, Chrissis and Van Hove [5] used Taboo search method for solving the scheduling problem. They used Java programming language for implementing the proposed model for 100 numbers of jobs over four numbers of machines.

Sels, Coelho, Manuel Dias, and Vanhoucke [6] developed three meta-heuristics for scheduling multiple jobs on non-related parallel machines to minimize total make span. The methods were based on GA, Taboo search and a combination of them including branch and bound method.

Ak and Koc [7] in their research paper discussed the GA approach and its operators, chromosome structure design for parallel machine scheduling and flexible job shop scheduling problems. Teekeng and Tammano [8] developed a modified GA to minimize the total make- span. Kim, Yun, Yoon, Gen, and Yamazaki [9] used a hybrid fuzzy GA to minimize the total make-span and total lateness penalty cost. Liu [10] also proposed a compound GA to minimize total lateness. He used a heuristic to assign high priority jobs to high priority machines.

Gen and Lin [11] designed a multi-objective evolutionary algorithm for solving different type of scheduling problems. They used the proposed method for solving job shop and flexible job shop scheduling problems.

Rostami, Ebrahimzadeh and Mahdavi [12] proposed a non-identical parallel machine multi-objective scheduling problem considering both the deterioration and learning effects. The processing times and due dates have been considered as uncertain fuzzy values. The authors developed a branch and Bound method for solving the proposed approach. Bandyopadhyay and Bhattacharya developed a modified evolutionary algorithm for solving multi-objective parallel machine scheduling problem [13].

Li, Amdeo, Yalaoeui and Chehade [14] also proposed a new approach for solving the parallel machine scheduling problem consisting n independent jobs on m identical parallel machines with release dates, due dates, and sequence-dependent setup times with no preemption of the jobs. The considered objective functions are minimizing total make-span and total tardiness. They used NSGA-II and SPEA-II evolutionary approaches for solving the proposed model and showed the advantages of NSGA-II approach for the studied problem.

Tavakkoli-Moghaddam, Taheri and Bazzazi [15] developed a novel, multi-objective model of a parallel machines scheduling problem that minimizes the number of tardy jobs and total completion time of all jobs. The proposed model, considers the machines as unrelated parallel units with different speeds. Besides, there is some precedence, relating the jobs with non-identical due dates and their ready times. Sequence-dependent setup times embedded in their proposed model may vary in different machines based on their characteristics.

Baesler and Palma [16] proposed a memetic algorithm combining the Genetic Evolution with local search for solving the parallel machine scheduling problem involving a molding production process in the wood industry. The algorithm was compared against four multiobjective techniques:   the multi-objective genetic algorithm (MOGA), the strength Pareto evolutionary algorithm (SPEA), the non-sorting genetic algorithm II (NSGA II), and multi-objective genetic local search (MOGLS). The Authors show that their proposed approach outperformed the benchmark techniques in most of the test problems based on two objectives of industrial interest: minimization of the maximum completion time and minimization of total tardiness.

• III.    The Proposed Mathematical Model

• 3.1    Indexes and Parameters

• 3.2    Decision Variables

• 3.3    Objective Functions

The main objective of solving the job shop scheduling problem, is finding the best feasible solution from the problem space which satisfies all the constraints. The time needed to find such a solution, highly depends on the program complexity and dimension. The scheduling problem must be first formulated under a given assumptions and next be solved using a proper approach. In this section, the proposed mathematical model for solving the parallel machine scheduling problem under the assumptions mentioned in section 1 is formulated and described.   They developed two multi-objective mathematical models, which consist of two and three inconsistent objective functions, respectively. The first model minimizes the total manufacturing cost and the total weighted tardiness simultaneously, while the second uses make-span an additional objective function.

The proposed model consists of the following indexes and parameters:

The main items of a linear mathematical model are decision variables that their final values are known as the final solution. The proposed model consists of two Boolean decision variables which are defined as below:

X[ 'I : Equal to1, if the l^th process of the j^th job should be processed by the i^th machine, otherwise zero.

Yljl'ji : Equal to 1, if l^th process of j^th job will be processed by i^th machine before the l'^th process of the same job, otherwise zero.

There are two objective functions in the proposed model defined as the following equations.

The make-span is the total length of the schedule (that is, when all the jobs have finished processing). The first objective function is defined to minimize the total makespan which is calculated by Equation 1.

Min T = ∑ 1=1 ^FTj                (1)

FTj = Max FT_t         ∀ Lj ∈ Pj         (2)

ft_l. =      ∗ ( ST_Lj + ^D4 )   ∀ Lj ∈ Pj , i ∈ I (3)

The second objective function is defined equation (4) in order to minimize total machine costs which include the processing costs plus the machine investment costs.

Min c = max Ci ∀ i ∈ I           (4)

Ct =        +∑ l=i ∑_∀ ∈ Pj Xiji ^∗ Ciji ∀ Ij ∈ Pj , i ∈ I

• 3.4    Constraints

The rest of the model includes some relations to guarantee the problem constraints and assumptions are considered and all obtained solutions are feasible. These relations are given as the follows.

∑ l^i xij = 1(6)

∑Si ∑∀ ij ∈ Pj xljt = 1(7)

4*vi

Ftji'ji ∗ ( ST_t-. ^- FT₄ )≥ Xlji ^∗ Xlji ^∗ Rljl'ji

• ∀ Ij , ^'7 ∈     ,   ≠ *-'j ,i∈I(8)

( °C ^- °Cj ) ∗ ( ST^ ^- ST_L,. ) ≥0     ∀ ^li , ^vi ∈ Pj , (9)

^4^^r j ∗ ( ST_Llj ^- FT_tj )≥0      ∀ h ^, i ^∈ Pj , (10)

min ( x₄i ∗ (1 - (| kt -^k₄|)),0)≥0

∀ i ∈ I , lj ∈ Pj ∃ kt , к ij (11)

The Equation 6 enforces processes of the jobs to be process just by one machine. Equations 7 and 8 show that one machine cannot perform more than one process at a time. Equation 9 makes the processes with higher priority to be performed before other processes of the same job, in case if equal priority, this constraint will have no effect. Equation 10 demonstrates the precedence relation between processes. The type conformity obligation between jobs and machines is considered by Equation 11.

• IV.    The Proposed Genetic Algorithm

The proposed mathematical model is a non-linear programming model and besides the NP-Hard nature of the problem, it will take a long time to solve the medium and large scale problems in real environment. Hence, a multi-objective GA based meta-heuristic approach is also developed for solving the proposed model. The pseudo code of the standard NSGA-II algorithm is given in Figure 1.

The proposed GA first generates the initial population randomly. Then, the fitness of each chromosome (solution) is calculated and is sorted based to create the Pareto frontiers. Non dominating solutions are placed on a front and the better solution among them is selected using the crowding distance concept. The main loop of the program generates next populations by producing Offsprings, merging with parents, sorting them and choosing the best solutions.

Initialize Population

Generate random population - size M

Evaluate Objective Values

Assign Rank (level) Based on Pareto Dominance - “sort" Generate Child Population

Binary Tournament Selection

Recombination and Mutation

Por i = 1 to Number of Generations

With Parent and Child Population

Assign Rank (level) Based on Pareto - “sort”

Generate sets of non-dominated fronts

Loop (inside) by adding solutions to next generation starting from the “first” front until M individuals found determine crowding distance between points on each front Select points (elitist) on the lower front (with lower rank) and are outside a crowding distance

Create next generation

Binary Tournament Selection

Recombination and Mutation Increment generation index End of Loop

Fig.1. The NSGA-II pseudo code [18]

• 4.1    Chromosome Structure

The chromosomes are the main core structures of the Genetic algorithm which encode the solutions and the proper representation of them is very important to ensure the efficiency of the algorithm. The chromosomes used in the proposed GA, are constructed from concatenating smaller chromosome structures (sub-chromosomes) for each job which are depicted in Figure 2. In the first generation, the value of the genes is non-repetitive permutation integers which are randomly assigned.

Machine 1 Machine 2 Machine 3 Machine 4

1 3 7 4 8 2 9 5 6

Fig.2 Sub-chromosome structure for each job

These sub-chromosomes demonstrate the machines assigned for process of a job. The length of the chromosome for job j is N j + M – 1 . The genes having values greater than N j are used as delimiters (black fields in Figure 1). For example, assuming N 1 =9 and M=4 (job #1 consists of 9 processes and four machines are available), the Figure 2 shows that processes {1,3,7} are assigned to Machine 1, {4,8,2} to Machine 2, etc.

The main chromosome structure is obtained by concatenating N numbers of sub-chromosomes which is shown in Figure 3.

Sub-chromosome of Job1

Sub-chromosome of Job2

…

Sub-chromosome of Job N

Fig.3. Chromosome structure of proposed GA

• 4.2    The Crossover Operator

The crossing over operator is needed to generate new chromosomes from the current population. Generally, good chromosomes (solutions) with a higher probability are good candidates to be mated hoping to generate better Offsprings. In the proposed GA, a one-point crossover operator is applied for every sub-chromosome of the selected parents. This may lead to infeasible off-springs if repetitive genes occur in a sub-chromosome which is not a permutation case. In order to solve this problem, after generating the Offsprings, the proposed algorithm checks for repetitive values and substitutes them with missing numbers. The details are depicted in Figures 4, 5 and 6.

Parent 1

Parent 2

2	3	4	1	5	6
3	6	2	4	1	5

Fig.4. One-point crossover operator

Offspring 1       2     3     4      1      1       5

Offspring 2       3      6      2     4     5       6

Fig.5. Offsprings having repetitive values

The crossover position in Figure 4 is selected between genes 4 and 5 and the children chromosomes (Offsprings) are generated. As it can be seen in Figure 5, the gene with value “1” is repetitive in offspring 1 and the value “6” is missing. The second Offspring also has a similar problem. This issue is solved by replacing the repetitive genes with missing value and is represented in Figure 6.

Offspring 1	2	3	4	6	1	5
Offspring 2	3	1	2	4	5	1

Fig.6. Modified Offsprings having repetitive genes

• 4.3    The Mutation Operator

• 4.4    Calculating the Fitness

• 4.5    Time Fitness

• 4.6    Cost Fitness

• 4.7    The NSGA-II Implementation

The second operator applied on some chromosomes of the population is mutation. This operator randomly selects a chromosome and exchanges its value (the machine assigned to a process of a job) with another value (machine) randomly. This exchange is applied on every sub-chromosome of the selected chromosome by changing the gene values. The feasibility of the mutated chromosome is always checked and in case of generating bad chromosomes, the changes are omitted. The probability of mutation is defined as 30 percent.

Calculating the value of the objective function(s) is the main part of the optimizing algorithms. The objective function computes the fitness (quality) of the obtained chromosomes (solutions). In the proposed GA algorithm, the fitness of each chromosome is computed in two points of view: time and cost. The details of each are described below.

To calculate the fitness of a chromosome, first it is decomposed to sub-chromosomes and genes are decoded to identify which processes of the jobs are assigned to which machines. When the machines assigned to processes of a job are distinguished, next it will be checked that whether the precedence relations between processes is maintained or not. If the answer is positive, the completion time of each job is calculated. The greatest (maximum) job completion time (make-span) is chosen as the first objective function value.

The calculation of the cost function is performed in a similar manner at the same time. While calculating the process time of the jobs, the computation cost is also considered and calculated. The maximum computed machine cost is chosen for the second objective function value.

The main ideas in multi-objective NSGA-II approach are dominance and crowding distance. Dominance is a public concept that is used in many multi-objective approaches. The solution x dominates solution y , if the value of all objectives for x solution are better (or at least equal to) than that of y solution. In this case, the x solution exists on a better Pareto Frontier than y and absolutely should be preferred. Otherwise, x neither dominates nor is dominated by y solution which means both solutions are on the same frontier (like x and z solutions is Figure 7). In this case, the crowding distance concept helps the decision makes to choose better solution [12].

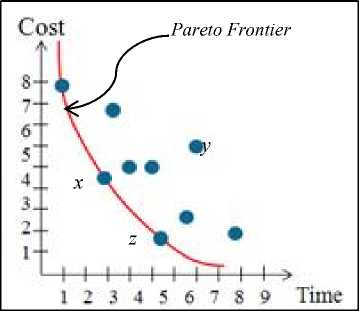
Fig.7. The dominance concept

The crowding distance is a criterion for comparing the solution on the same frontier. Naturally, solutions covering larger spaces of the Pareto frontier are better than the solution with smaller coverage because the probability of ignoring other solutions is less. This criterion is defined as the largest rectangular consisting the current solution which does not contain other solutions [12]. This concept is depicted in Figure 8.

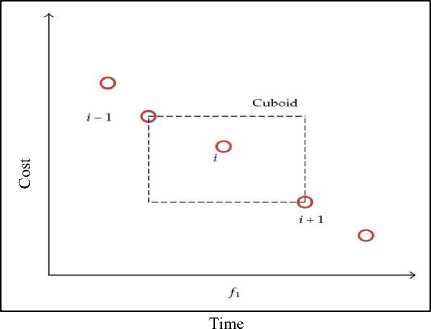
Fig.8. The solution i has a larger crowding distance than its neighbor solutions

• V.    Computational Results

The proposed model is implemented in Matlab on a PC running Windows 7 with 4.2 GHz processor. The simulation parameters and the specification of test cases are given in Table 1 and Table 2 respectively.

Table 1. The simulation parameters

Parameter	Value
Population Size	50
Number of Iterations	200
Crossover Probability	0.8
Mutation Probability	0.3

Table 2. Specification of implemented examples

Example #	Number of Jobs	Number of Machines
1	5	5
2	5	10
3	10	5

Each of the examples listed in Table 2 have been executed 30 times and the minimum completion time, average of minimum completion times, minimum cost and the average of minimum costs are shown in Table 3.

Table 3. Obtained results of running the examples for 30 times obtained by NSGA-II approach

	Minimum Completion Time	Average of Minimum Completion Times	Minimum Cost	Average of Minimum Costs
Example 1	139	141.2	537	543.6
Example 2	115	120.4	332	341.6
Example 3	425	439.4	966	982.3

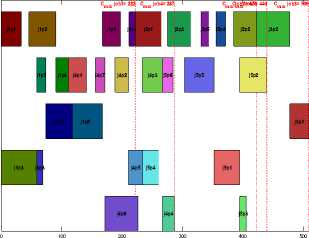
The simulation results for one of the final solution selected from the Pareto frontier of Example #1 are depicted in Figures 9 and 10. The Figure 9 shows the Gantt chart of the processing time of the activities of the jobs (horizontal axis) and assigned machines (vertical axis).

Gantt chart

M5

M4

M3

M2

M1

Time

Fig.9. Gantt chart of final solution obtained for Example 1

The cost Gantt chart for the same solution is illustrated in Figure 10.

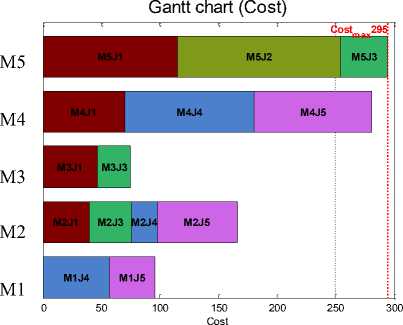
Fig.10. Gantt chart of machine cost of the same solution

The proposed model is also implemented using MOPSO approach. The obtained results are given in Table 4. Comparing the results obtained by two approaches, shows that NSGA-II method has a slightly better performance in solving the proposed algorithm

Table 4. Obtained results of running the examples for 30 times obtained by MOPSO approach

	Minimum Completion Time	Average of Minimum Completion Times	Minimum Cost	Average of Minimum Costs
Example 1	142	146.7	566	581.1
Example 2	117	123.1	335	341.0
Example 3	433	440.9	977	981.5

• VI.    Conclusion

  In this paper a new mathematical linear programming model for scheduling the jobs in a parallel environment to minimize the total machine cost and the completion time is proposed and due to NP-Hard nature of the problem and the complexity of the proposed algorithm, a multiobjective meta-heuristics based on NSGA-II and MOPSO are developed for solving the model. The proposed method is implemented in Matlab R2009a (in a PC running Microsoft Windows 7 with 2 GB of RAM and 4.2 GHz main processor) and tested for three case studies of different sizes. The obtained results show the efficiency of the proposed mathematical model and the developed GA algorithm. Besides, the better performance of NSGA-II in comparison with MOPSO approach for solving the proposed model is identified.