A Multidimensional Extended Neo-Fuzzy Neuron for Facial Expression Recognition
Автор: Zhengbing Hu, Yevgeniy V. Bodyanskiy, Nonna Ye. Kulishova, Oleksii K. Tyshchenko
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 9 vol.9, 2017 года.
Бесплатный доступ
An article introduces a modified architecture of the neo-fuzzy neuron, also known as a "multidimensional extended neo-fuzzy neuron" (MENFN), for the face recognition problems. This architecture is marked by enhanced approximating capabilities. A characteristic property of the MENFN is also its computational plainness in comparison with neuro-fuzzy systems and neural networks. These qualities of the proposed system make it effectual for solving the image recognition problems. An introduced MENFN’s adaptive learning algorithm allows solving classification problems in a real-time fashion.
Computational Intelligence, Facial Expression, Image Recognition, Extended Neo-Fuzzy Neuron, Machine Learning, Data Stream
Короткий адрес: https://sciup.org/15010964
IDR: 15010964
Текст научной статьи A Multidimensional Extended Neo-Fuzzy Neuron for Facial Expression Recognition
Automatic analysis of signals on a human face is used in different subsystems of vision, including tracking a viewing direction and focus of attention, lip reading, bimodal speech processing, synthesis of visual morphemes, forming teams based on facial expressions. Tracking the viewing direction or focus of attention can be used for releasing a user from using a mouse or a keyboard. To realize a robust speech interface, the speech lip reading opportunity can be very useful. Automatic detection of fatigue, boredom and stress will be valuable in situations where some constant attention is crucial for a person, for example, onboard the aircraft or while driving a truck, a train or a car. In real-world applications, this sort of tasks is usually solved by means of various fuzzy clustering techniques [1-6]. Identification of such facial expressions is based on processing real-time video streams, where the required features are allocated. Thus, recognition of facial expressions may be reduced to clustering multidimensional data in a real-time mode.
A goal of the developed research is to synthesize a clustering architecture, which enables distributing the real-time multivariate data through a set of clusters automatically.
Fuzzy Inference Systems (FISs) and Artificial Neural Networks (ANNs) have dilated into a large class of Data Mining problems of variant nature under conditions of the prior doubt and instant ambiguity. Hybrid neuro-fuzzy systems (HNFS) [7-10] combine learning abilities typical for artificial neural networks as well as both interpretability and results’ "clarity" peculiar to fuzzy inference systems. Basic limitations of the hybrid neuro-fuzzy systems are simulation awkwardness and a quite slow training speed.
To overpass some of the outlined above problems, a neuro-fuzzy system also known as a “neo-fuzzy neuron” (NFN) was taken into consideration and explored in [1113]. Fig.1 gives a demonstration of the neo-fuzzy neuron’s organization.
The NFN structure is a non-linear learning mechanism that has control over multiple inputs and an only one output. This framework generally brings into action a presentation n y=£ fi(x) =1
where x is a component i of the n - dimensional vector of input signals, x = ( x ,,..., x ,..., xn ) T e Rn , y denotes a scalar output for the NFN. NFN’s structural blocks are non-linear synapses NS that guarantee a non-linear permutation for the component i of x in the type of
h f (x) = EwM (xi) I=1
where w stands for a synaptic weight l of the nonlinear synapse i, I = 1,2,...,h, i = 1, 2,...,n; ци (x) signifies a membership function l in the nonlinear synapse i , which finally yields a fuzzified element x . In this way, an NFN-implemented conversion may be marked down in the following manner
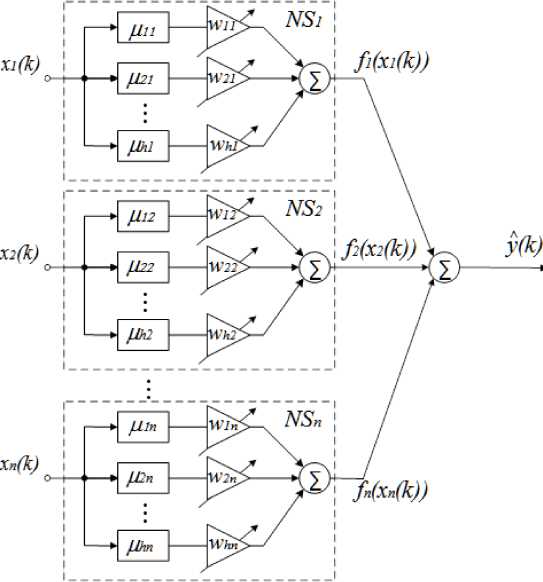
Fig.1. A neo-fuzzy neuron
nh y=ЁЁ w/i^/i (xi). i=1 I=1
An NFN-realized fuzzy inference is given by
IF xt IS xu THEN AN OUTPUT IS wu, I = 1,2,. ..h x ci-1,
--------------, if x i e L c i - 1, i , c / , i J , c i , i - c i - 1, i
|
M "=' |
c i + 1, i - x |
ff x i e[ c i , i , c i + 1, i |
|
c i + 1, i - c i , i , |
||
|
0, |
otherwise |
where c specifies selected (usually distributed uniformly) centroids (at random fashion) of membership functions in the interval [0,1], although in a natural way 0 < xt< 1.
NFN’s inventors [11-13] brought into requisition common triangular frameworks as membership functions that meet the requirements of the unity partition.
Certainly, some other functions apart from triangular frameworks may be employed as membership functions, first of all, B-splines [14-18] that proved successfully their effectiveness just being parts of the neo-fuzzy neuron. A generalized view of B-spline-based membership functions of the q - order may be put forward in the shape of
J, if x i e[ c ii , c i + 1, i 0, otherwise
q = 1,
> for
|
M if ( x i , q ) = < |
x i - c ii M if ( X i , q - 1 ) + c i + q - 1, i c ii |
|
|
+ c i + q , i - X i |
- M i + 1,i ( x, q 1 ) |
|
|
C i + q - 1, i - C i + 1, i |
||
|
for q > 1, i |
= 1, 2, ..., h - q. |
|
In case when q = 2 , the conventional triangular constructions are gained. It also bears mentioning that the B-splines may ensure the unity partition by way of
h
£ M (xi-, q ) =1
i = 1
which are non-negative, i.e.
h
У A f ( x i , q ) ^ 0 l = 1
and have a support area
Consequently, the input vector signal
x ( k ) = ( x ( k ) ,..., x ( k ) ,..., xn ( k ) ) (here k = 1,2,...
marks a current discrete time indicator) being fed to the NFN’s input yields a scalar value at its output nh y (k )=УУ wAk-1) au( xi(k)) (1)
i = 1 l = 1
where wu ( k - 1 ) stands for a current value of tuned synaptic weights to have been gained (as a result of learning) by previous ( k - 1 ) observations.
Bringing in the membership functions’ (nh x 1) - vector
a ( x ( k ) ) = ( A ( X ( k ) ) ,..., A h 1 ( X ( k ) ) ,
A1 (X1 (k)) ,-.., Al2 (X2 (k)) ,-, Au (Xi (k)) ,-, Ahn (Xn (k))) and w(k-1) = (wn (k-1),...,wh 1 (k-1),W21 (k-1),..., wli (k-1) ,..., whn (k-1))T which conforms with the vector of synaptic weights, the conversion (1) carried out by the NFN may be marked down in a slightly different manner y (k) = wT (k-1) a(x(k)). (2)
To set the NFN’s parameters, its developers put into use the gradient procedure for minimization of a training criterion
E ( k ) = 1 ( У ( k )- У ( k ) ) 2 = 1 e 2 ( k ) =
-
1 (,xl
= o| У ( k ) - УУ wA^ x i ( k ) ) I
-
2 V i=1 l=1
and has the shape of
W li ( k ) = wu ( k - 1 ) + ne ( k ) am ( x- ( k ) ) =
= w li ( k - 1 ) + П ( У ( k ) - У ( k ) ) Au ( X ( k ) ) =
= w,( k -1) + n | У (k )-УУ^Д xi( k ))|A,(Xi( k)) V i=1 l=1
where y ( k ) designates an external reference signal, e ( k ) denotes a learning error, n refers to a parameter of a learning rate.
To speed the NFN’s training process up, a special-type algorithm was introduced in [19] having both tracking (for processing non-stationary signals) and filtering (for "noisy" data) properties w (k) = w (k -1) + r-1 (k) e (k) a( x (k)),
< 2 (3)
r ( k ) = a r ( k - 1 ) + || a ( x ( k ))|| ,0 < a < 1.
In the circumstances of a = 0 , the scheme (3) is credible in its organization to the one-step Kaczmarz-Widrow-Hoff learning algorithm [20], and when a = 1, it’s similar to the method of stochastic approximation by Goodwin-Ramage-Caines [21].
It will be observed that training the NFN’s synaptic coefficients (weights) can be utilized by an amount of other methods for identification and learning inclusive of the common least-squares method with its upgrades.
-
II. An Extended Neo-Fuzzy Neuron
As previously stated, the neo-fuzzy neuron’s non-linear synapse NS performs the zero-order Takagi-Sugeno inference, which is in fact the elementary Wang-Mendel neuro-fuzzy system [22-24].
It seems certain that approximating inferiorities of this system may be amended by dint of a system node also known as an “extended non-linear synapse” ( ENS , Fig.2). A framework of an “extended neo-fuzzy neuron” [25-26] (ENFN) is built with reference to the ENS elements in exchange for the common NS nodes.
By establishing several additional variables
У a ( x i ) = An ( X ) ( w l 0 + w 1i x 1 + w 2 x2 + ... + w p x p ) , h
0 11 22 pp
I \ I ) A-i^h V i )\ li li i li i ..... li i / l=1
= W u A u ( Xi ) + w 1 i X 1 A 1i ( X i ) + ... + W 2- X 2 A 1 i ( X i ) + ...
+ w P X A 1 i ( x i ) + ... + w 2i A i ( Xi ) + ... +
+wpxpA2i (xi) +... + whpixpAhi (xi), w = (w0, w1i,..., 4, w0i,..., wp-,..., whi-) T,
A (xi) = (m (xi), w (xi)..... xt^u (x), a i (x),..., xpM1 (xi),->xpMhAxi))T , we can note down г (xi ) =wT M xi],(4)
nn y=Z fi (x)=L wT A(xi )=wT A( x)
=1
where wT = ( w T ,..., wT ,..., w T ) , and
T
T
A ( x ) = ( A ( x l ) ,-’ A T ( x i )..... tt ( x n ) ) .
As one can notice, the ENFN embodies ( p + 1 ) hn synaptic weights to be tweaked, and a fuzzy output performed by every ENS takes on a form
IF x IS x THEN AN OUTPUT IS w0 + wx +... + wx, l = 1,2,...,h (6)
which is essentially in agreement with the p -order Takagi-Sugeno inference.
It should be also marked that ENFN stands seized of a simpler architecture as opposed to the common neuro-fuzzy system that leads to its simplified numerical realization.
When the ENFN’s input is given as a vector signal x ( k ) in the system, there appears an output scalar value
y ( k ) = wT ( k - 1 ) A ( x ( k ) ) (7)
whereby the listed above expression stands out from the formula (2) only by the fact that it embraces ( p + 1 ) times more parameters to be set as contrasted with the conventional NFN. It stands to reason that ENFN settings may be trained with the algotirhm (3) that acquires in this case a shape of
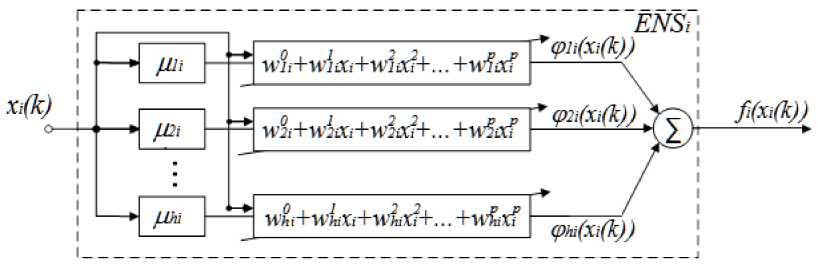
Fig.2. An extended non-linear fuzzy synapse
w ( k ) = w ( k - 1 ) + ( 1/ r ( k ) ) e ( k ) a ( x ( k ) ) , r ( k ) = a r ( k - 1 ) + || a ( x ( k ))|| ,0 < a < 1.
Fig.3 displays a scheme of an extended neo-fuzzy neuron.
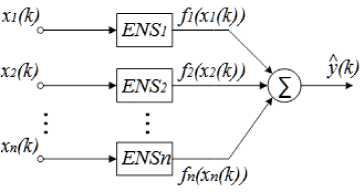
Fig.3. An extended neo-fuzzy neuron
The extended neo-fuzzy neuron is a building block for the multidimensional neo-fuzzy neuron (MENFN). Its architecture is depicted in Fig. 4.
That looks on reasonable grounds to put in several layers in the MENFN for solving the pattern recognition task. The first layer encapsulates the extended neo-fuzzy neurons, and their quantity brings into accordance with the output vector’s ym ( k ) dimensionality.
A quantity of non-linear synapses that configures each neo-fuzzy neuron complies with dimensionality of the input feature vector x ( k ) . The succeeding layer represents an activation function
a( k ) = v (yj(k)) (9)
where v (y(k )) =
y j ( k ) , if y j ( k ) > 0
0, otherwise
An output layer of the MENFN computes values
Vj (k) in response to the positive rationing j k )=
v j ( k ) m , T v vj ( k ) = 1
which is necessary if a learning vector is set in the range [0,1].
If a learning vector utilizes the numerical coding of an output signal, the MENFN performs a fuzzy conjunction of elements in the output vector ^ (k)
u ( k ) = sup { v ( k ) } . (11)
j = 1 v
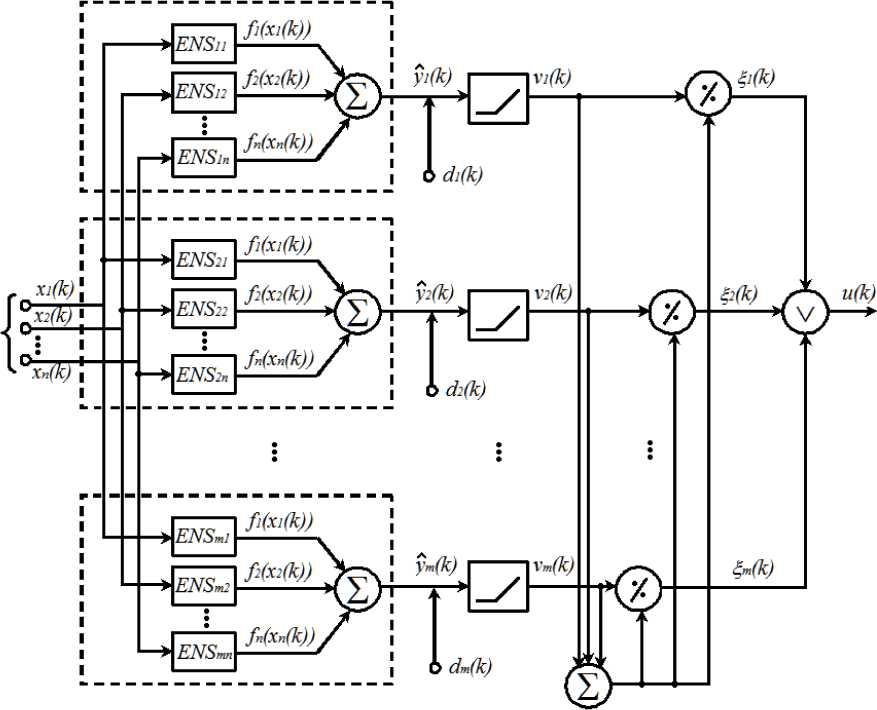
Fig.4. A multidimensional extended neo-fuzzy neuron
-
III. Experiments
To bear out superiority of the architecture under consideration, several experiments were carried out for the task of basic emotions’ recognition. Several depictions from the open-source database Psychological Image Collection at Stirling (PICS) [27], as well as some illustrations partly from the Cohn-Kanade (Extended, CK+) database [28] and some other images taken from public access were mainly used as objects for recognition.
The learning dataset contains 344 depictions; learning was repeated during 30, 50, and 80 epochs as the case may be. For the algorithm (8), a learning rate 1/ r = n was taken equal 0.75. A capacity of membership functions for every ENS equals 9; the fuzzy inference represented by the ENS can be put down like
IF x IS x THEN AN OUTPUT IS w0 + w1Xi +... + wlpxp, l = 1,2,..., h and agrees with the Takagi-Sugeno inference of the second order.
As noted above, a quantity of neo-fuzzy neurons m measures up dimensionality of the output vector. Seven basic emotions are selected for recognition: anger, disgust, fear, surprise, happiness, sadness, and neutral expression. Therefore, m = 7. The character features’ vector contains the two-dimensional coordinates of 35 feature points position (Fig.5) [29].

Fig.5. Arrangement of control points
So, dimensionality of the input vector xn ( k ) equals 70.
The MENFN’s framework confirms a sufficiently higher learning rate as opposed to a scheme described in [30]. A plot for errors’ change by epochs is shown in Fig.6; results of learning are demonstrated in Table 1. The algorithm was tested on a sample of 78 images.
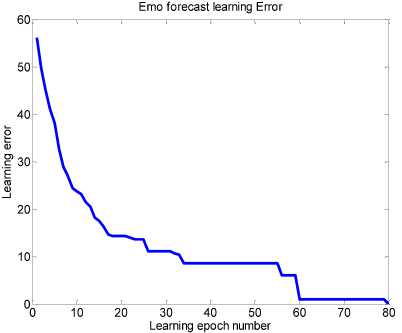
Fig.6. Dependency of a learning error on a number of learning epochs
The developed framework of multidimensional extended neo-fuzzy neuron definitely provides both a high learning rate and the high recognition accuracy for multidimensional data. These inferiorities are particularly useful for detecting facial expressions in a real-time mode.
Table 1. Training MENFN for recognition of 7 emotions. Results
|
Basic emotions |
A number of images in the training set |
Percentage of unrecognized images, % |
||
|
30 epochs |
50 epochs |
80 epochs |
||
|
Anger |
49 |
2 |
0 |
0 |
|
Disgust |
66 |
0 |
0 |
0 |
|
Fear |
35 |
0 |
0 |
0 |
|
Happiness |
45 |
2 |
0 |
0 |
|
Sorrow |
19 |
5 |
0 |
0 |
|
Surprise |
50 |
0 |
0 |
0 |
|
Neutral |
80 |
4 |
3 |
0 |
-
IV. Conclusion
The paper proposes a structure of the multidimensional extended neo-fuzzy neuron which is an extension of the conventional neo-fuzzy neuron for a case of the fuzzy inference procedure when its order is higher than a zero order and which possesses both a multidimensional data input and an output. The proposed learning algorithm allows distributing effectively the aggregate data into an amount of previously known clusters. The considered MENFN enhances clustering qualities, incorporates both a high training speed and its quite simple numerical feasibility.
Acknowledgment
This article gets sponsored by RAMECS and CCNU16A02015.
Список литературы A Multidimensional Extended Neo-Fuzzy Neuron for Facial Expression Recognition
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and V.O. Samitova,"Fuzzy Clustering Data Given in the Ordinal Scale", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.1, pp.67-74, 2017.
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and V.O. Samitova,"Fuzzy Clustering Data Given on the Ordinal Scale Based on Membership and Likelihood Functions Sharing", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.2, pp.1-9, 2017.
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, V.O. Samitova,"Possibilistic Fuzzy Clustering for Categorical Data Arrays Based on Frequency Prototypes and Dissimilarity Measures", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.5, pp.55-61, 2017.
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, V.M. Tkachov, “Fuzzy Clustering Data Arrays with Omitted Observations”, International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.6, pp.24-32, 2017.
- Ye. Bodyanskiy, O. Tyshchenko, and D. Kopaliani, “An Evolving Connectionist System for Data Stream Fuzzy Clustering and Its Online Learning”, Neurocomputing, 2016 (article in press).
- Ye. Bodyanskiy, O. Tyshchenko, and D. Kopaliani, “An evolving neuro-fuzzy system for online fuzzy clustering”, Proc. Xth Int. Scientific and Technical Conf. “Computer Sciences and Information Technologies (CSIT’2015)”, pp.158-161, 2015.
- L. Rutkowski, Computational Intelligence. Methods and Techniques. Berlin Heidelberg: Springer-Verlag, 2008.
- C.L. Mumford and L.C. Jain, Computational Intelligence. Berlin: Springer-Verlag, 2009.
- R. Kruse, C. Borgelt, F. Klawonn, C. Moewes, M. Steinbrecher, and P. Held, Computational Intelligence. A Methodological Introduction. Berlin: Springer-Verlag, 2013.
- Ye. Bodyanskiy, “Computational intelligence techniques for data analysis”, in Lecture Notes in Informatics, 2005, P-72, pp.15–36.
- T. Yamakawa, E. Uchino, T. Miki and H. Kusanagi, “A neo fuzzy neuron and its applications to system identification and prediction of the system behavior”, Proc. 2nd Int. Conf. on Fuzzy Logic and Neural Networks “IIZUKA-92”, pp. 477-483, 1992.
- E. Uchino and T. Yamakawa, “Soft computing based signal prediction, restoration and filtering”, Intelligent Hybrid Systems: Fuzzy Logic, Neural Networks and Genetic Algorithms, Boston: Kluwer Academic Publisher, pp. 331-349, 1997.
- T. Miki and T. Yamakawa, “Analog implementation of neo-fuzzy neuron and its on-board learning”, Computational Intelligence and Applications, Piraeus: WSES Press, pp. 144-149, 1999.
- J. Zhang and H. Knoll, “Constructing fuzzy-controllers with B-spline models – Principles and Applications”, Int. J. of Intelligent Systems, vol.13, pp.257-285, 1998.
- V. Kolodyazhniy and Ye. Bodyanskiy, “Cascaded multiresolution spline-based fuzzy neural network”, Proc. Int. Symp. on Evolving Intelligent Systems, pp.26-29, 2010.
- Ye. Bodyanskiy, O. Tyshchenko, and D. Kopaliani, “Adaptive learning of an evolving cascade neo-fuzzy system in data stream mining tasks”, Evolving Systems, Vol.7, No.2, pp.107-116, 2016.
- Ye. Bodyanskiy, O. Tyshchenko, and D. Kopaliani, “A hybrid cascade neural network with an optimized pool in each cascade”, Soft Computing, Vol.19, No.12, pp.3445-3454, 2015.
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and O.O. Boiko, “An Evolving Cascade System Based on a Set of Neo-Fuzzy Nodes”, International Journal of Intelligent Systems and Applications (IJISA), Vol.8, No.9, pp.1-7, 2016.
- Ye. Bodyanskiy, I. Kokshenev, and V. Kolodyazhniy, “An adaptive learning algorithm for a neo-fuzzy neuron”, Proc. 3rd Int. Conf. of European Union Soc. for Fuzzy Logic and Technology (EUSFLAT’03), pp.375 379, 2003.
- S. Haykin, Neural Networks and Learning Machines (3rd Edition). NJ: Prentice Hall, 2009.
- G.C. Goodwin, P.J. Ramage, and P.E. Caines, “Discrete time stochastic adaptive control”, SIAM J. Control and Optimization, Vol.19, pp.829-853, 1981.
- L.X. Wang and Mendel J.M., Fuzzy basis functions, universal approximation and orthogonal least squares learning. IEEE Trans. on Neural Networks, Vol.3, pp.807-814, 1993.
- L.X. Wang, Adaptive Fuzzy Systems and Control. Design and Stability Analysis. Upper Saddle River: Prentice Hall, 1994.
- S. Osowski, Sieci neuronowe do przetwarzania informacij. Warszawa: Oficijna Wydawnicza Politechniki Warszawskiej, 2006.
- Ye.V. Bodyanskiy and N.Ye. Kulishova, “Extended neo-fuzzy neuron in the task of images filtering”, Radioelectronics, Computer Science, Control, Vol.1(32), pp.112-119, 2014.
- Ye. Bodyanskiy, O. Tyshchenko, and D. Kopaliani, “An Extended Neo-Fuzzy Neuron and its Adaptive Learning Algorithm”, I.J. Intelligent Systems and Applications (IJISA), Vol.7, No.2, pp.21-26, 2015.
- http://pics.psych.stir.ac.uk/2D_face_sets.htm
- Handbook of Face Recognition. London: Springer-Verlag, 2011.
- P. Lucey, J.F. Cohn, T. Kanade, J. Saragih, Z. Ambadar, and I. Matthews, “The Extended Cohn-Kanade Dataset (CK+): A complete dataset for action unit and emotion-specified expression”, Proc. IEEE workshop on CVPR for Human Communicative Behavior Analysis, San Francisco, USA, 2010.
- N. Kulishova, “Emotion Recognition Using Sigma-Pi Neural Network”, Proc. 2016 IEEE First International Conference on Data Stream Mining & Processing (DSMP), pp.327-331, 2016.


