A New Algorithm for Voting in Social Networks

Published Online September 2014 in MECS DOI: 10.5815/ijitcs.2014.10.05

A social network is a social structure made up of a set of actors (such as individuals or organizations) and the ties between these actors. Voting plays an important role in democratic systems. It is an effective means to reflect the majority's intention within a limited amount of time. However, it is also true that voting is not a perfect solution for making decisions.

The recent development of computer and communication technologies and the digitalization of information are producing new ways of "democratic" decision-making. For example, page-ranking systems by search engines and recommendation systems of online shopping sites use such "democratic" systems.

In the world of real politics, this kind of "democracy has not been acclaimed yet. A voter still does not want to use a computerized system to recommend a candidate whose policy perfectly matches his/her preferences. Decision-making by delegation networks in organizations depends on rich social capital. Social capital includes trust, norms of reciprocity, and networks of civic engagement [1].

The phenomenon known as Web 2.0 gathers attention trends such as blogs (diaries) and social networking services (SNS), where individuals transmit information and share it on the internet, are becoming prominent. SNS can be thought of as one example of the utilization of delegation networks in organizations. In SNS, one can search for a key person who is knowledgeable in a certain field of study and entrust that expert with one’s vote.

In SNS, users can visit key persons’ pages and find out what they say in their diaries, as well as their comments made on other diaries. We assume that key persons are those who have many networks of contacts (the number of “friends” in the SNS), comment on various employees’ diaries, and write appropriate comments. They are also unique persons whom many employees pay attention to.

Other employees can visit these key persons’ pages directly and it may enhance awareness for these employees. Social capital in social networking services enhances decision-making[2].

In this paper, we will propose a new way of decisionmaking with the help of a representative democracy voting. In this model we introduce a committee who are participated in voting rather than their group. Firstly we use community detection techniques in order to obtain parties(group). We divide the graph since we want to choose a committee uniformly from the entire graph. Next, we clarify proportion of each party in committee, How many people from each party must be member of committee. Finally, we use links webpages algorithms for ranking users in each party and then we choose top ranking users according to proportion of party in committee.

• II.    Transitive proxy voting system

A voting system [3, 4] is a set of rules that a community adopts to take collective decisions. It specifies the way the voters express their preference (sometimes called the ballot ), and the algorithm that determines the final outcome (sometimes called the tally). Voting is done for basically one of two purposes: to decide on a motion (e.g., to pick the best among a series of alternatives), or to elect a representative or set of representatives (e.g., to elect a senate). In both cases the final goal is that making decisions which reflect as much as possible the opinion of the citizens. The difference is the way that is pursued.

The former case, known as direct democracy , is based on the idea of ensuring maximum equality and fairness by making all citizens vote directly for the different motions. Direct democracy works better in practice for small cohesive groups. When public decisions reach a certain level of complexity, it becomes impractical for every citizen to become fully informed on every issue [5].

The latter case, known as representative democracy , involves a relatively small number of representatives who are elected by the citizens to take decisions on their behalf. Beyond the issue of which representation structure is the most appropriate for a given context, representative democracy presents certain risks in practice. For instance, by concentrating power in the hands of a small political elite, it creates fertile ground for corruption, entrenchment, conflict of interest, etc., which may result in bad government [5].

A third way, combining the benefits of direct and representative democracy while avoiding some of their drawbacks, is the so called delegative democracy which is based on proxy voting [6,7]. In this context a citizen can decide either to express directly her opinion on an issue, or to delegate her vote to a proxy, that is, another citizen that she trusts [5].

This voting system seems well suited for online social networks. In fact, people’s social connections can be seen as a mixture of strong ties (family, close friends) and weak ties (distant friends, acquaintances). Electronically-mediated social networks allow people to maintain many more weak ties than before. This means that the number of connections they have is larger than what one could consider an actual “friendship” network. On the other hand, current social networks are mostly networks of peers, in which the “super-stars” (the individuals with the larger number of connections) do not have the visibility that can be achieved through mass media. The “superstars” in a social network may be known by only a tiny fraction of the network [5].

Proxy-voting systems encourage people to cooperate to build direct, permanent political and social relationships with each other and with their individual supporters, forming a web of trust. Everyone can achieve political influence proportional to their level of public support [5].

To describe a voting system we need to specify how thevoters express their preference (sometimes called the ballot ) and the algorithm that determines the final outcome (the tally).Note that there are also technical issues with how the voting is concretely carried on, such as establishing the identity of participants- this is an important topic on its own, that can be solved through various technical means, but that we are notgoing to address here[8].

Various possible choices exist for defining the ballot. “One-vote” voting systems are those in which a voter picks exactly one candidate; in our case, one contact. In a “ranked” voting system, each voter would rank her contacts in order of preference, and in a “rated” voting system, voters would give a score to each contact[8].

In the following we consider the simpler one-vote kind Of ballot, where participants choose to delegate their decision to exactly one of their contacts, or to vote for themselves, which corresponds to not delegating the vote further[8].This ballot can be interpreted as the creation of a delegation graph . A delegation graph is a directed graph built over the undirected underlying friendship social graph: it can contain cycles and it can have selfloops representing the choice of some electors not to delegate their vote and instead to express directly their opinion on the matter of the voting. Fig.1 illustrates an example of delegation graph induced over a social network[8].

Our system considers that each person in the network receives a certain amount of score (weight); the score will then be used to decide among the possible alternative motions or to elect a committee. There are many ways of computing this score from a delegation graph, a trivial one being the sum of all votes received. Here we propose a more complex tally, namely transitive proxy voting with exponential damping. This is similar to standard proxy voting but with a damping factor that introduces some reluctance in the way delegated votes are transferred. This reluctance, controlled by a parameter α, corresponds intuitively to the idea that, in an electronically mediated social network, typically you cannot fully trust your connections, and you want to refrain from giving them all of your delegation. But more importantly, you do not know how far your liquid vote can go on the network hop-by-hop: even if you fully trust your proxy, can you transitively fully trust your proxy’s proxies?[8].

Reluctance makes the vote less liquid, reducing its strength with each delegation step, and thus limiting the distance it can travel. Reluctance makes the vote viscous . We might call this form of proxy voting a viscous democracy because of the way trust (and consequently a vote’s weight) decays with the distance[8].

• III.  Voting In Social Network

The class of social networks under examination have mutual (symmetric) friendship relationships. They are modeled by means of an undirected graph of friendship, say G=(V G ,E G ) defined by a set of vertices (or nodes) V G and a symmetric set of edges E_G C V_G x V_G . We let for every x e V g , N g ( x ) = { y |( x , y ) e E g } (the neighbors of x in G ). For the sake of presentation, we will assume that G is connected; this is not a limiting assumption as our results can be easily extended to deal with disconnected components [5].

The key aspect of the voting system that we propose for social networks is that votes can be delegated transitively along the existing edges of the social network. That is, any member of the network can choose a proxy among her contacts. A person can also choose not to delegate her vote.

Besides the obvious organizational advantages, the assumption that votes can only be assigned to a direct connection is twofold: on one hand, voters can base their decision on a direct personal knowledge of the person they vote for, making propaganda essentially useless and thus decoupling popularity from credibility; on the other hand, the fact that mandates are attributed through a chain of direct connections should ensure a stronger sense of responsibility [5].

Every node x ∊V chooses exactly one of his neighbors in G and delegates to her. More formally, the voters’ choices are expressed by a voting function (or simply “voting”), a function v: V_G→V_G such that one has v(x) ∊ N G (x) for all X e V . The set of all voting functions for G is denoted by Vot G . For every v e Vot_G we let D=(G,v) be     the     directed    graph     (V,A)    where

A = {(X, v(X)) | X e v} . For persons that do not delegate, we include a self-loop in the delegation graph, implicitly assuming a self-loop at each node in the friendship graph [5].

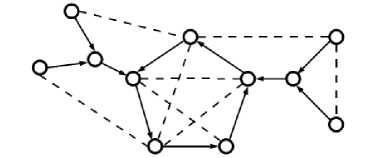
Fig. 1. An example of delegation graph over a social network. Delegation are represented by solid arcs, the reminder connections by dashed edges.

• IV.  Ranking Users

• A.    Transitive Proxy Voting and Page Rank

In PageRank, the arcs of a directed graph represent Hyperlinks between web pages, and a hyperlink is seen as a way to confer authority. More precisely, every time a page x points to a page y , x is transferring a part of its own authority to y ; more precisely, if x points to k pages, its authority will be equally distributed among those pages [5].

Although there are many equivalent ways to define PageRank formally, for our purposes it is convenient to introduce it using the path formula of [9]: given a directed graph D=(V G ,E G ) , and for a fixed α ∊ [0 1] referred to as the damping factor, we define the PageRank of node x ∊ V D as:

r D ( x ) = 1- ^ Z aⁿ br ( n ) (1) n D ne path ( - , x )

where n_D = | V_D | (the number of nodes of D ), Path D ( -, x ) is the set of all directed paths of D ending in x and the branching of a path is defined as follows:

br ( x , x

, xk + 1 ) =

| N D ( x 1 )|...| N D ( X k )|

ND (z) = {w |(z, w) e ED } where N +D ( z ) is the set of out-neighbors of z.

Every node x receives its importance (its delegations) through incoming paths: every incoming path gives a contribution that depends on the number of branches the path contains, and that decays exponentially with its length. The PageRank formula can also be applied to an undirected graph, by looking at an edge e = { x , y } as if it were a pair of arcs

( x , y ) , ( y , x ) .

Let us adopt the PageRank method in our context: we define the score of node x for the voting function v as r D ( G , v ) (x), the PageRank of x in the directed graph D(G, v). Note, however, that the PageRank formula applied to such simple graphs turns out to be much easier to analyze. In a graph with out-degree 1, the branching factor is always 1; so we can write:

ri

^{(1 - а} )

n

Z a p p e path ( - , x )

This voting system depends on a single parameter α. In the following, we discuss its properties for “small enough” and “large enough” values of α .

• B.    Parameter α

There is a single parameter α controlling the voting process, which can be understood as the delegation factor, the amount of its own power that a person can delegate to another person.

If the delegation factor is small (close to 0), mandates become undelegable. This means that only direct votes count, and the resulting process can be described as a simple majority voting [8].

If the delegation factor is large (close to 1), most nodes that delegate their mandate to someone else. The winners are chosen simply by the size of the sub-tree to which they belong (i.e., the number of people that voted for them, directly or indirectly) [8].

In Fig. 2 we depict an example. when α = 0.2 (left), node 5 (which has many more direct supporters than the others) has the largest score; when α = 0.9 (right), the higher degree of transitivity makes the node 7 with the largest score. Also observe that in this case node 8 is slightly stronger than node 9 because although 8 has fewer direct supporters she receives part of the influence of node 7.

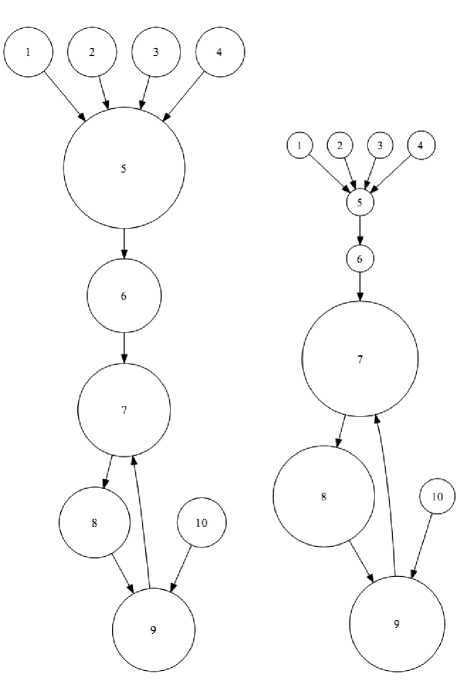
Fig 2. Scores computed on a delegation graph with damping factor α=0.2 and α=0.9. The size of the nodes is proportional to their scores.

• V. Proportionality Using Delegation Graph

In the case of an election for selecting a committee of representatives deal with a particular group of issues. In this case self-loops in the delegation graph indicate citizens that accept to be possibly elected in the committee, in other words, node with a self-loop indicate their willingness to b considered as candidates. When a committee having s seats must be selected, we can simply choose the s top scoring candidates. However, there is an opportunity of selecting a committee that represents the diversity of users, by ensuring proportionality. The criterion of proportionality states that each political alliance should have a share of the seats proportional to its share of the votes [8].

The concept of party or alliance can be mapped easily into our voting system. In absence of specific alliances declared beforehand, a voting system for social networks may interpret the connected components of the delegation graph as alliances, as they represent communities of people who delegate to other members of their community but not to aliens [10].

This allows for proportionality understood as picking, for each connected component of the delegation graph, the top-k scoring nodes, in which k is proportional to the size of the connected component. For example, suppose that we have to assign s seats and that we have c communities with n1, . . . , nc members, respectively: we can assign to the i-th community ki = ni. c/(n1 + . . . + nc) seats, choosing the ki top scoring nodes within that community. The method for allocating the number of seats for each party can be determined by any system for proportional voting. We describe here the use of D’Hondt rules [11], which are a proportional representation system used for the parliament of several countries, and in the European Parliament elections. Nevertheless we stress that most of the arguments that follow apply to other proportional voting systems.

Under D’Hondt rules seat allocation is done roundwise. In each round the new seat is assigned to the party with the highest ratio m/( s + 1) , where m is the size of each party(group), and s is the number of seats that party has been allocated so far[8].

An example is shown in Tabel 1. In the example m 1 = 12, m 2 = 8, m 3 = 5 and s = 3, the numbers in the table are the ratios, and the first group gets two seats, the second group gets one seat, and the last group gets zero seats.

Tabel 1. Seat allocation via D’Hondt rule
	C 1	C 2	C 3
1st Seat	12	8	5
2nd Seat	6	8	5
3rd Seat	6	4	5

• A. Community Detection Technique in Social Network

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into (potentially overlapping) sets of nodes such that each set of nodes is densely connected internally. We can see three community in Fig. 3.

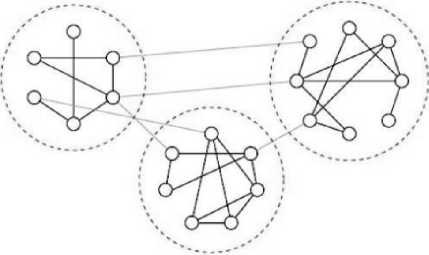
Fig. 3. Three community in a friendship graph

Community detection is useful in real networks because it is more likely that nodes in one community have same properties. Community detection methods in social networks are similar to graph partitioning. Communities are useful in many applications. Web clients clustering (community detection) which have same or similar interests or near together via location can improve the World Wide Web services performance. One of the community detection benefits is to provide better recommendation systems for efficient customer’s guidance and increasing the business opportunities via representing the lists of retailer items which produces the clusters of customers with similar interests. The goal of graphs community detection is the identification of modules and their hierarchical structure by using the information which is encoded in graph topology [12].

Finding communities in complex networks is revealed recently by many authors. Researchers proposed different methodologies for finding such communities in various fields like physics, statistics and data mining[4,13,14]. We use community detection base vertex similarity. In the following, we describe this method [15].

Vertex similarity is defined in terms of similarity of their social circle, e.g, the number of friends two share in common. Two nodes are structural equivalence, if they are connecting the same set of nodes in a network. Nodes of the same equivalence class form a community [15].

Since structural equivalence is too restrictive for practical use, other definition of equivalence such as Jaccard similarity and Cosine similarity are proposed. Jaccard similarity defines as follow:

I N i n N j |

Jaccard ( v , v ) =----------- (4)

i,    j INuNI

In the equation N i is the neighbors of node v i . The range of Jaccard similarity value is between 0 and 1.

In community detection base vertex similarity, Firstly,we compute similarity matrix (Jaccard similarity) between every two nodes, then we use K-Means algorithm for clustering nodes.

• VI.    Exprimental result

For experimental work, we choose two social networks.

• 1)    Zakhary Karate Club Network: This network belongs to a karate club in one the universities in America. This dataset describes the personal relations between members of a karate club and was created by Zachary [16], who studied the friendship of 34 members of a karate club over a period of two years and analyzed how the club is divided into two new clubs after an internal conflict. Zachary could show that the personal relations where a good indicator for the prediction of which member joined which of the new founded clubs. This dataset has been used by several authors to evaluate their methods. It has 34 nodes and 78 edges. 2) Dolphin Social Network: An undirected social network of frequent associations between dolphins in a community living off Doubtful Sound, New Zealand[17]. It has 62 nodes and 159 edges.

Firstly, we compute an adjacency matrix, then obtain similarity matrix with Jaccard formula between every two nodes. With K-means algorithm, we cluster similarity matrix and get the parties (groups). We clarify proportion of each party in committee via D’Hondt rules. Finally we rank users in parties with formula 1 and select top rank users in every party according to their proportion. These users form a committee and they participate in voting rather than entire social network.

The proposed approach that has been written in MATLAB and is tested on two social network datasets. You can see output of it in Fig.4 and Fig.5. Gray nodes form a committee.

• VII.    Conclusion

The main problems of voting in social networks are the existence of many weak links, the fact that even the most well-known users are not known by many, and the low voter turnout in general. We are convinced that a transitive proxy voting is the best choice in such a setting.

We propose an algorithm for representative democracy voting. In this kind of voting users select a committee who are participated in voting rather than entire social network. Our algorithm has three steps.1) Community detection for finding parties in the network 2) Clarifying proportion of each party via D’Hondt rule. 3) Ranking users and finding important users in every party.