A New Ant Colony Optimization Algorithm Applied to Optimizing Centralized Wireless Access Network

Published Online March 2014 in MECS

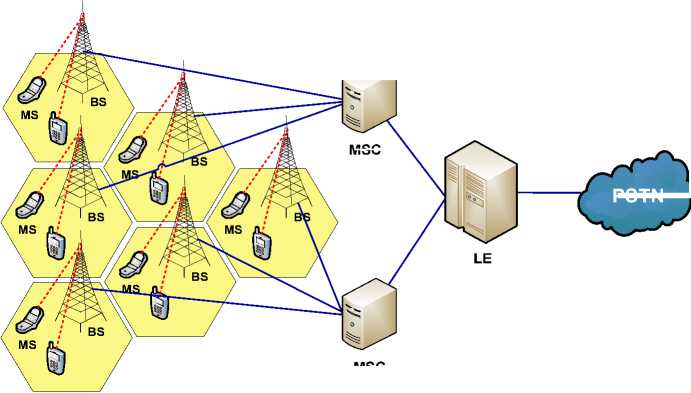
The wireless access network of a cellular telephone system consists four interacting layers. These layers are the mobile station or user equipment layers, the base transceiver stations layer, the mobile switching centers layer, and lastly local exchanges of the public switched telephone network (PSTN). Each cell in the hexagonal cell grid contains one base station (BS) and mobile station (MS). A set of BS’s are physically connected to and served by a mobile switching center (MSC). In turn, a set of MSC’s are physically connected to and served by a local exchange (LE). Fig.1 depicts the general configuration of a cellular access network. Each BS is typically assigned a group of radio channels ( frequency carriers ) to support a number of mobile stations in its cell. BS’s at adjacent cells are assigned different sets of frequencies. The antennas of a BS are designed to achieve coverage only within the particular cell. By limiting coverage of a BS to its cell area, the set of frequencies assigned to this BS can be reused at other BS’s that are distant enough to keep co-channel interference within acceptable limits.

MSC

PSTN

MSC

Fig. 1: A cellular access network

A BS contains the radio transceivers defined for its cell, and handles the radio-link protocols with the user’s wireless device (cell phone). In addition, it may house a controller that handles radio-channel setup, frequency hopping and handovers. In a large metro area, a potentially large number of BS’s are deployed at pre- determined locations. The BS controllers are connected by land-wires to nearby MSC’s in the area. The MSC provides all the functionality needed to handle a mobile subscriber, such as registration, authentication, location updating, handovers, and call routing to a roaming subscriber. To switch calls from/to local mobile users to/from remote users, MSCs are connected by landcables to nearby LEs of the PSTN. The potential locations of MSCs are judiciously determined with respect to the BS locations and to the LEs in the region. Typically, the locations of the LEs are fixed, and a single LE serves an area with many BS’s and multiple MSCs [1-2].

In the latest paper [3], we have proposed a novel Particle Swarm Optimization (PSO)[4] algorithm based on Ford-Fulkerson algorithm find maximum flow in networks for the optimal location of controllers in a mobile communication network. In [5], the authors have presented the topological design of the network connecting the BSs to the MSCs and the MSCs to the LEs in a typical region of the cellular system. The access network has a centralized tree topology. That is, a single LE facility controls a set of MSCs, and a single MSC controls, in turn, a set of BS’s. Finally, a BS supports a group of mobile stations through wireless connections. A tree topology of the wireless access network, consisting of 1 LE, 2 MSCs, 4 BSs, and 18 MSs is shown in Fig.2.

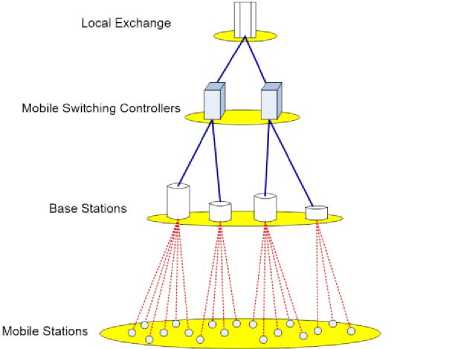
Fig. 2: A Centralized access network

The topological design of access networks has been very important part of cellular network research in recent years. Recent studies are given in references [59]. Generally, the design problem is formulated as a constrained optimization problem, where the goal is to find a network topology such that an objective function is optimized, subject to a set of constraints. The objective function may be the total cost, or some performance measure like utilization, call blocking or throughput. The constraints may be bounds on link capacities, cost elements, or some network performance measure. However, the optimization problem is too complex, or it’s computationally impractical to search for the optimal solution. So, one usually resorts to heuristic methods that enable one to determine a nearoptimum network topology more easily. The simple design of access network has one single LE. The objective function is the total cost of connecting the BSs to the MSCs, and connecting the MSCs to the LE. Authors in [6] proposed an exhaustive search algorithm to generating all the possible matrices and searches for the matrix that yields the minimum cost. In [7-9], the authors presented a heuristic algorithm to finding the best solution is the topology with the smallest cost across all the iterations.

In this paper, we propose a novel Ant Colony Optimization (ACO) algorithm [10] to finding the total cost of connecting the BSs to the MSCs, and connecting the MSCs to the LE. Numerical results show that our proposed algorithm is much better than previous studies. The rest of this paper is organized as follows: Section 2 presents the problem formulation the simple centralized access network. Section 3 presents our new algorithm for optimization wireless access network based on ACO algorithm. Section 4 presents our simulation and analysis results, and finally, section 5 concludes the paper.

• II.    Problem Formulation

• 2.1    The Simple Centralized Wireless Access Network

The simple centralized access network can be defined as follows [5]: Let N be the number of BSs ( T , T ,..., T ). The locations of the N terminals are assumed known and fixed. Let M be the number of potential sites ( S , S ,..., S ), where up to M MSCs can be placed. In one extreme situation, none of the M sites is used, and all the N BSs are linked directly to the central LE, S₀ .

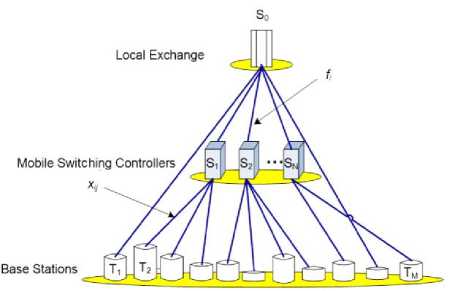
Fig. 3: Simple centralized access network

In the other extreme, all the M MSC sites are used, each serving a subset of BS’s. The principal constraint is that the MSC at site S j can handle up to a maximum of P j BSs( j = 1.. M ) . This can be a hardware limitation, or a capacity constraint of the land-cable connecting the MSC to the LE. The central site is assumed to have no such constraint.

We want to formulate the network design problem as an optimization problem. Let c ij be the cost of connecting base station T i to MSC site S j or to the central site S 0 . The cost c ij is measured in some unit (e.g., dollar/month ), and represents the overall BS-MSC connection cost (e.g., transmission cabling, interfacing, maintenance, leasing ). Note that a base station may be located at the site of an MSC, in which case the corresponding c ij cost is zero.

These cost elements c ij can be written in the form of a matrix, as follows:

	" C 10	c 11	••   C 1 M "
C = ( Cy )     = \ ij NX x M +1	c 20	c 21	c 2 M	(1)
	V CN 0	cN 1	• •  CNM J

If a MSC at site S j is utilized, the MSC capital cost and its connection cost to the LE are also incurred. Let f j be the cost of connecting an MSC at S j to the central LE S 0 , and b j the capital cost of the MSC at S j . We can write these 2 costs as row vectors, as follows:

Note that since a BS may be connected to at most one of the M MSC sites or to the central LE site, there must be only one “1” in each row of matrix X . In addition, note that the number of 1’s in column j is the number of BSs connected to the MSC at site S j ( j = 0.. M ) . Thus, an all-zero column of matrix X corresponds to an MSC site that is not used.

Displayed equations or formulas are centered and set on a separate line (with an extra line or half line space above and below). Displayed expressions should be numbered for reference. The numbers should be consecutive within each section or within the contribution, with numbers enclosed in parentheses and set on the right margin. From matrix X , we extract the following MSC-usage vector:

Y = ( У 0 , V 1 ,-, У м ) ⁽⁶⁾

where, the element variable y j ( j = 0.. M ) is defined as:

N

• 1    if S. used , if Z x„ >  0

i                    Z=1 ij

• V, = 5

jN

• 1    if S, not used , if Z Хц = 0

I               i                               i =1 ^ij

| F = ( f o , f_v_ f M ) [ B = ( b ₀, b _p..., Ь м )

The cost of a network design (defined by matrix X and vector Y ) is thus expressed as follows:

We assumed that the capital cost of the central LE is not counted. That is, b 0 =0, and clearly f 0 =0. Similarly, we can write the MSC constraints as the following row vector:

P = ( P c , P 1 ,~, P m )

where, p j is the maximum number of BSs that MSC at site S j can handle ( j = 1.. M ) , with p₀ = N (i.e., the central LE can handle all the N base stations).

A network design can be defined by the following matrix variable:

X = ( x. )

V ij NN x M +1

Х10

x20

VXN0

xM x 2 M xNM J

where, the element variable x j (i = 1.. N , j = 0.. M ) is defined as:

• 1 1    if T is connected toS.

xe =h.'

^ij 0 if T is not connected toS ij

NM       MM

Z = Z Z \Cx X x + z f. X y + z b. X i=1 j=0V ij ij ’ j=0VJj jjJ j=0V j   jj’(8)

^ Z = sumdiag ( C x X T ) + F x Y ^T + B x Y ^T

In (8), the superscript T means transpose of matrix or vector, and sumdiag ( A ) is a function that sums up the diagonal elements of matrix A . The first term in the cost function Z is the cost of connecting the N BSs to the M MSCs used or to the central LE, the second term is the cost of connecting the MSCs to the LE, and the third term is the hardware cost of the MSCs used.

• 2.2 The Optimal Centralized Wireless Access Network

The optimal centralized wireless access network (OCWAN) in network design problem can thus be stated as the following optimization problem.

Problem instance:

• • A set of BSs at known locations:

T 71 T

• ₁, ₂,..., _N .

• •    A set of possible MSC sites:

S 1 , S 2 ,..., S M .

• •    BS-connection cost matrix:

C = ( C, )

ij N x M +1

• •    The cost of connecting an MSC at S j to the central LE

• S 0 :

F = ( f o , f l ,..., f_M )

• •    The capital cost of the MSC at S j :

B = ( b 0 , b 1 ,..., b M )

• •    The mux capacity constraint vector:

^P = ( P 0 , P 1 ,-, P m )

Objective function: Find the matrix X (thus the vector Y ) that minimizes the network cost Z :

Z = sumdiag ( C x X T ) + F x Y T + B x Y T ^ min (9)

Subject to the following 2 constraints:

• •    The first constraint indicates that the sum of the elements in row i of matrix X must be 1 ( i =1,2,…, N ). E is the column vector of all 1’s.

X x E = E                             (10)

• •    The second constraint indicates that the sum of elements in column j of matrix X must be less than or equal to P j ( j = 0.. M ) .

E T x X <  P                              (11)

In the matrix inequality of (11), the inequality relation is defined element by element.

• III.    Ant Colony Optimization for OCWAN
  
  3.1    Ant Colony Optimization

• 3.2    Solving the OCWAN based on ACO Algorithm

The ACO algorithm is originated from ant behavior in the food searching. When an ant travels through paths, from nest food location, it drops pheromone. According to the pheromone concentration the other ants choose appropriate path. The paths with the greatest pheromone concentration are the shortest ways to the food. The optimization algorithm can be developed from such ant behavior.

The first ACO algorithm was the Ant System [10], and after then, other implementations of the algorithm have been developed [11-12].

In this section, we present application of ACO technique for the OCWAN problem. Our new algorithm is described as follows. We consider that configurations in my algorithm are sets of N BSs and set of M MCSs.

The encoding of the configuration is by means of matrix k , say k = ( х_ц ) n _x m +1 , ( i = 1.. N , j = 0.. M ) where x_y=1 means that the corresponding BS T i has been connected to MSC site S j , and otherwise x ij = 0 means that the corresponding BS T i has been not connected to MSC site S j . We use fully random initialization in order to initialize the ant population.

We present Ant_Repair function to ensure that the ant k satisfies constraints in (10) and (11) show in Fig.3.

ANT_REPAIR FUNCTION ALGORITHM ⁽ k = ⁽ x j ) n _x m +1 )

Input: The ant k

Output: The ant k will satisfies constraints in (10) and (11)

{FOR i=1..N ri = Number of 1s in row i

IF r i >1

Select (ri -1) 1s randomly and removes them from row i

ELSE IF Count i <1

Adds 1 1s in random positions in row i.

ENDIF

ENDFOR

FOR j=0..M cj = Number of 1s in column j

IF ( c j > p j )

Select (c j - p j ) 1s randomly and removes them from columnj

ELSE IF ( c j < p j )

Adds (p j -c j ) 1s in random positions in column j.

ENDIF

ENDFOR}

Fig. 3: Ant_Repair algorithm

After that, the ant k will have the sum of the elements in row i of matrix k must be 1 ( i =1,2,…, N ) and the sum of elements in column j of matrix k must be less than or equal to P j ( j = 0.. M ) . In our case the pheromone matrix is generated with matrix elements that represent a location for ant movement, and in the same time it is possible receiver location.

The Fig.4 presents process of our algorithm to solving OCLP based on ACO.

We use real encoding to express an element of matrix A N*M+1 (where N is the number of BSs, M is number of MCSs). Each ant can move to any location according to the transition probability defined by:

Dk ЪТЫ!Pj = s[., ]• [n; ]e               (12)

l e Nik where, τ is the pheromone content of the path from BS Ti to MCS Sj, Nk is the neighborhood includes only locations that have not been visited by ant k when it is at BS Ti, ηij is the desirability of MSC Sj, and it depends of optimization goal so it can be our cost function. The influence of the pheromone concentration to the probability value is presented by the constant α, while constant β do the same for the desirability. These constants are determined empirically and our values are α=1, β=10.

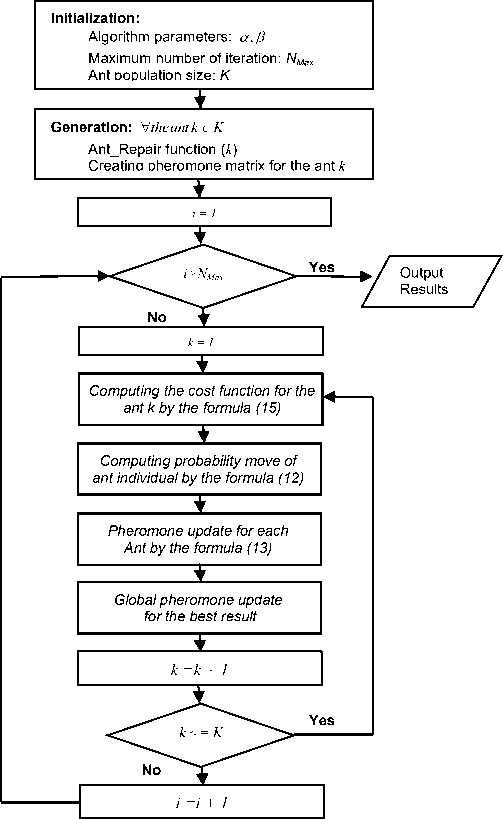
Fig. 4: Ant Colony Optimization algorithm

The ants deposit pheromone on the locations they visited according to the relation.

new      current

τ = τ   + Δ τ

k

j

where Δ τ ^k is the amount of pheromone that ant k exudes to the BS T i when it is going from c BS T i to MCS S j . This additional amount of pheromone is defined by:

Δ τ ^kj

С- ij

In which, c ij is the cost of connection between BS T i to MCS S j .

The cost function of the ant k is given by:

f = sumdiag ( C × k ^T ) + F × Y ^T + B × Y ^T        (15)

In which, Y defined in (7) and (8). The stop condition we used in this paper is defined as the maximum number of interaction N_max ( N_max is also a designed parameter).

• IV.    Experiments and Results

For the experiments, we have tackled several OCWAN instances of different difficulty levels. There are 8 OCWAN instances with different values for N and M , and BS-connection cost matrix show in Table 1.

Table 1: The experimental of the problems tackled

Problem #	Number of MSCs	Number of BSs
#1	4	10
#2	5	20
#3	8	40
#4	10	80
#5	20	100
#6	40	150
#7	50	200
#8	60	250

We have already defined parameters for the ACO algorithm in Table 2 below:

Table 2: The ACO algorithm specifications

Ant Population size	K = 100
Maximum number of interaction	N Max = 500
Parameter	α=1, β=10

The experiment was conducted on Genuine Intel® CPU DuoCore 3.0 GHz, 2 GB of RAM machine. We ran experiment ACO algorithm, Exhaustive Search algorithm [5] and Heuristic algorithm [8] implemented using C language. The experimental results of our algorithm was finally compared with others algorithm shown in Fig.5.

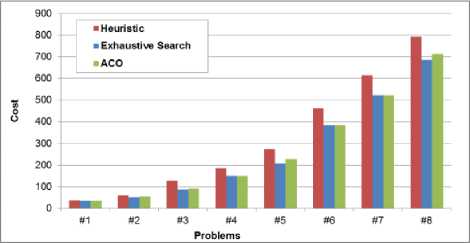
Fig. 5: The results obtained in the OCWAN instances tackle

The results show that the objective function values of our algorithm has achieved a much better than a Heuristic algorithm and approximate good solutions of Exhaustive Search algorithm. But, the performance of our proposed algorithm is better than other algorithm. The comparison of time processing shows in Fig.6.

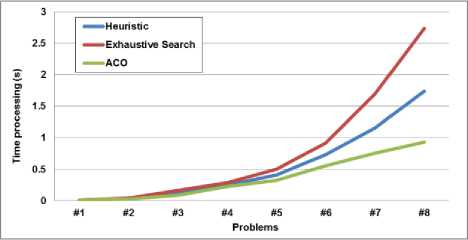
Fig. 6: The comparison of time processing OCWAN instances tackle

• V.    Conclusion

In this paper, we have proposed a novel Ant Colony Optimization (ACO) algorithm to finding the total cost of connecting the BSs to the MSCs, and connecting the MSCs to the LE called by the optimal centralized wireless access network. Numerical results show that performance of our proposed algorithm is much better than previous studies. With a growing need for anywhere and anytime access to information and transaction, optimal capacity expansion of wireless networks to accommodate next-generation wireless service is our next research goal.