A New Approach for the Generalized First Derivative and Extension It to the Generalized Second Derivative of Nonsmooth Functions
Автор: Hamid Reza Erfanian, M. H. Noori Skandari, A.V. Kamyad
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 4 vol.5, 2013 года.
Бесплатный доступ
In this paper, first derivative of smooth function is defined by the optimal solution of a special optimization problem. In the next step, by using this optimization problem for nonsmooth function, we obtain an approximation for first derivative of nonsmooth function which it is called generalized first derivative. We then extend it to define generalized second derivative for nonsmooth function. Finally, we show the efficiency of our approach by evaluating derivative and generalized first and second derivative of some smooth and nonsmooth functions, respectively.
Generalized Derivative, Smooth and Nonsmooth Functions, Linear Programming, Optimization
Короткий адрес: https://sciup.org/15010413
IDR: 15010413
Текст научной статьи A New Approach for the Generalized First Derivative and Extension It to the Generalized Second Derivative of Nonsmooth Functions
Published Online March 2013 in MECS
One of the most important concepts of nonsmooth analysis is the study of the generalized derivative (GD). In various fields such as optimization, control theory, differential equations, mechanics and economic when studying problems for different classes of nonsmooth functions, GD successfully has been applied. For instance, GDs use in solving of problems which mechanical engineers survey the evolution of rigid bodies that is subject to velocity jumps and force discontinuities as a result of friction and impacts. In addition, GDs use in solving of many areas problems such as diodes and transistors in electrical circuits or in problems of switching systems that arise in air traffic management, scheduling of automated railway systems and economic models of markets. In general, all systems contain switching systems that treat in nonsmooth systems (for more details see [1] and references therein).
There are some of well known generalized first derivative (GFD) especially Clarke GD [2], Ioffe prederivative [3] and Mordukhovich coderivative [4,5] (for more details see [6]). On the other hand, generalized second derivative (GSD) has developed because of its application importance in many of problems of applied mathematics and engineering including variational inequalities, semi-infinite programming, penalty functions, optimization problems and especially sensitivity analysis of optimal solutions involve nonsmooth functions. Many authors have defined GSD in different ways, for instance Lemarechal and Nurminski [7], Hiriart-Urruty [8], Aubin [9], Auslender [10] and Chaney [11], Ben-Tal and Zowe [12-14], Rockafellar [15], Cominetti and Correa[16] ( for more details see [17]).
In spite of the existence of different methods for GD, we see some restrictions and difficults in all of existing works in definitions of GFD and GSD, which it has been caused these GDs cannot use in applied problems. For example in these works, the nonsmooth function f (.) must be locally Lipschitz or convex and the points of nonsmoothness of nonsmooth function f (.) must be known. Moreover, the concepts limsup and liminf are applied to obtain the GD in which calculation of these is usually hard and complicated, and in general, deriving the GFD and GSD are very difficult and complex. It is therefore natural that we achieve a useful and practical approach for defining GD. This paper is basically an extended version of the results presented in [18]. Our intention here is to propose a useful and practical definition for GFD and in what follows, we will extend it to a new GSD (see [1] for application of practical new GFD in order to solve nonsmooth ordinary differential equations).
The structure of this paper is as follows. Section 2 defines GFD of nonsmooth functions which is based on functional optimization. Section 3 introduces a new definition for GSD based on last section. Some numerical examples and conclusions of this paper will be stated in Sections 4 and 5, respectively.
-
II. GFD of Nonsmooth Functions
We mainly utilize the new GD of Kamyad et al. ([18]) for nonsmooth functions. This kind of GD is particularly helpful and practical when dealing with nonsmooth continuous and discontinuous functions and it can be easily computed. In deriving our approach; first we introduce a functional optimization problem that its optimal solution is the derivative of smooth function on interval [ 0,1 ] . For solving this problem, we consider a linear programming problem and by solving it for nonsmooth functions, we obtain an approximate derivative for these functions on interval [ 0 , 1 ] which is GFD. In what follows, let us now devote just a short section to the generalized derivative of Kamyad et al. ([18]).
Let V = vk (.) : vk ( x ) = sin( k 7r x ): x E [0, 1 ], k = 1, 2 ,... .
For given function f(x) on [0,1] , define the following functional optimization problem:
In what follows, the problem (1) is approximated as the following finite dimensional problem ([18]):
N1
Minimize J(g(.)) = ^ JQ vk(x)g(x) dx - Ak k1
subject to si
J | f (x)- /(si Hx-si )g(si) dx < e62, si
g(.) CC[0,1], si e( 1,-), i = 1,2,...,m mm where N is a given large number. We assume gi = g (si), fi1 = f(si - f2 =f(si + ^
that and
f = f S) for all i = 1,2,..., m . In addition, we choose the arbitrary points s. e (i—1, —), i = 1,2,...,m. By i mm trapezoidal and midpoint integration rules, problem (2) can be written as the following problem which
J vk(x)g(x) dx-\
Minimize J (g (.)) = ^
k1 subject to si
J I f ( x )- f(s i )-( x-s i )g(s i ) dxx< 261 , si
g(.) CC[0,1], si €( 1,-), i = 1,2,...,m mm
gx , g 2,..., gm are its unknown variables:
Minimize subject to
N
E k1
vkigi k i1
I f 1 - fi +6gi | + | f 2- f-^i | < i = 1,2,..., m .
where vk (.) e V , A k = -J^ v k ( x ) f ( x ) dx , к = 1 , 2 , 3 ,... and , are positive sufficiently small numbers.
Theorem II.1 (see [18]) : Let f (.) e C 1 [0,1] and g * (.) e C [ 0,1 ] be the optimal solution of the functional optimization problem (1). Then f '(.) = g * (.).
Definition II.2 (see [18]) : Let f (.) be a nonsmooth continuous function on the interval [ 0,1 ] and g (.) be the optimal solution of the functional optimization problem (1). We denote the generalized first derivative (GFD) of f (.) by GFdf (.) and define as GFaf (.) = g *(.).
Remark II.3: Note that if f (.) is a smooth function on [ 0,1 ] then the GFdf (.) in definition II.2 is f '(.) . Further, if f (.) is a nonsmooth integrable function on [ 0,1 ] then GFD of f (.) is an approximation for first derivative of f (.) .
Lemma II.4 : Let pairs ( v *, u ), i = 1,2,..., m be the optimal solutions of the following LP problem:
m
Minimize v i1
subject to v. > u, v. > —u, v. > 0, u. E I . i ii ii i
Then u *, i = 1,2,..., m are the optimal solutions of the following nonlinear programming problem (NLP):
Minimize uI
ui i1
where I is a compact set.
Proof: Since (v*, u*), i = 1,2,..., m are the optimal solutions of the LP problem, so they satisfy the constraints. Thus we have vu and ii
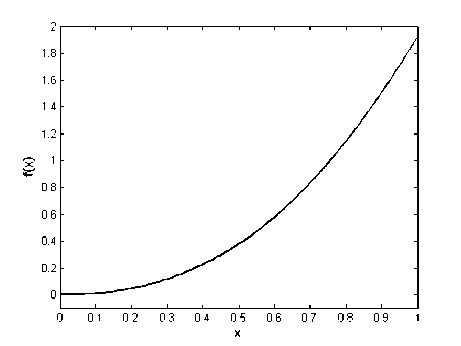
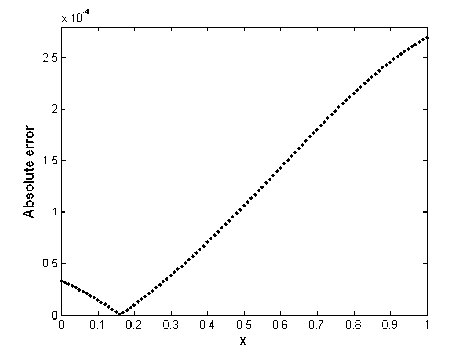
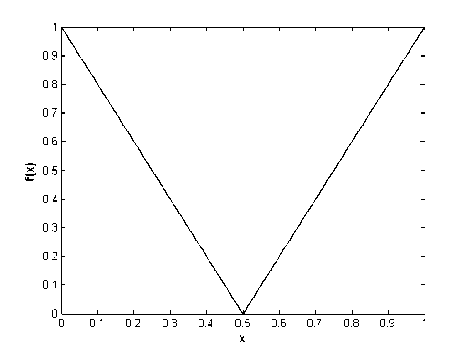
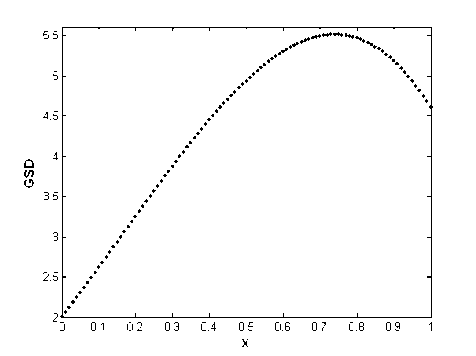
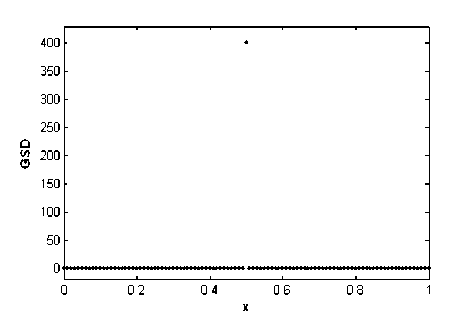
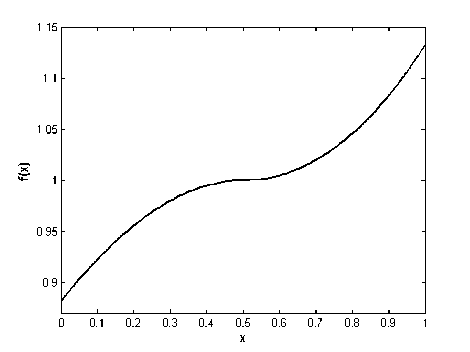
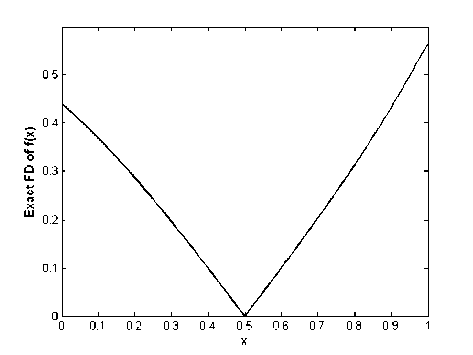
v* > —u* for i = 1,2,...,m . Hence, |u*| mm existu* I I, i = 1,2,...,m such thatu* < У? иа i1i1 Define, v* = u* for i = 1,2,...,m . Then v* > u ,iiii mm and vu. Moreover, vu and hence i1i1 mm mm vi ui ui i1 i1 i1 mm So vv,this is a contradiction. ii i1i1 Now, by Lemma II.4 and techniques of mathematical programming, problem (3) can be converted to the following equivalent linear programming problem which gt, i = 1,...,m , р,к, k = 1,2,...,N and uj., z, u, v. for i = 1,2,..., m are decision variables of iiii the problem: N Minimize k1 m subject to - lk ■ 'V/gil X , i0 m k-6Y,vki9i<-Xk, i0 (ui+vi) + (^i+zi )<£б, ui - vi - g9t = f 1 -fi, ш. — z. + 6g. = L, — f, iiii2i ш.,z,u,v , > 0, г, г, i, i, rk ~ , k = 1,2,...,N; i = 1,2,...,m smooth functions on an interval. By using this problem for nonsmooth functions, we approximate the second order derivative of these functions on an interval which is GSD. Firstly, we consider again Lemma II.1 in [18] and state the following theorem and prove it where C2[0,1] is the space of twice differentiable functions with the continuous derivative on [0,1]. Theorem Ш.1: Let f (.) eC2[0,1], g(.) e C[0,1] and J v(x)g(x) — v\x)f (x) dx = 0 for any v(.) E C2[0,1] where v(0) = v(1) = v'(0) = v'(1) = 0 . Then we have f nQ = g(.). Proof: We use integration by parts twice and conditions v(0) = v(1) = v'(0) = v'(1) = 0 : J v''xc) f (x) dx= v'(1) f (1) -v'(0) f (0)- J v"(x) f 'xx) dx 00 = — J v'xx) f \x) dx = - v(1) f '(1)- v(0) f '(0)- J v(x) f "(x) dx = J v(x) ff'xc) dx. Here J v'\х)f (x) dx = J v(x)f "xx) dx. (5) where Xk for k = 1,2,3,..., N satisfies in relation. Ak = ~fo vk(x)f(x)dx, k = 1,2,3,... Remark II.5: Note that and are sufficiently small numbers and points s. €( —, —), i mm i = 1,2,..., m can be chosen as arbitrary numbers. Remark II.6: Note that if g*. i = 1....m are the i, , , optimal solutions of problem (4), then GFdf S) = g*, i = 1,2,..., m. III. GSD of Nonsmooth Functions In this section, based on Section 2, we introduce an optimization problem similar to the problem (1) whose the optimal solution is the second order derivative of On the other hand, by assumptions of theorem, we have: J" v (^x)f (x) dx = ^ v(x)g(x)dx. (6) Therefore, by (5) and (6) Г v(x) f X)) - g(x) dx = 0. (7) So using equation (7) and by Lemma II.1 we have v(.) f "C) - g(.) =0orf "C) = g(.) .□ Let the set V = vk(.) : vk(x) = 1 — cos(2k7rx): x E [0,1], k = 1,2,... . Then v(0) = v(1) = 0 and vz(0) = vz(1) = 0 for all vk(.) e V. We note that V is a total set in U = v(.) e C2[0,1]: v(0) = v(1) = v'(0) = v'(1) = 0 . So for any V(.) E U there exist coefficients a^, a^,... in К such that v(x) = 52ал(x) x€[0’ 1],vk(.)Vv. (8) k Theorem Ш.2: Let f (.), g(.) e C2[0,1] and Jo vk(x)g(x)~ v”(x)f (x) dx = 0 for any vk(•) VV where v (0) = v (1) = v z(0) = v z(1) = 0 . Then we have f"(.) = g(.). Proof: By attention to the relation (8) and the proof of Theorem III.1, we can conclude the proof of this theorem. Theorem III.3: Let 0 be a given small number, f (.) EC 2[0,1] and mE N. Then there exist 0 such that for all si J I fXх) - f 'ss)) - (x - si)f"ss)) dxx<£ si Minimize I(g(J) E Jovk(x)g(x) dx-^ subject to si J | h(x) - h(si) - (x - si )g(si) | dx < £<52, s i i1i g(.) CC[0,1], si G (-----,—), i = 1,2,...,m mm Ak = jovk (x)f ^xx) dx, and if f (.) E C 1[0,1] , then h(.) = f'(.) and otherwise h(.) = GFdf(.) which the function GFdf (.) is the GFD of f (x) (see [18]). Theorem III.4: Let f(.) e C2[0,1] be given and g*(.) EC[0,1] is the optimal solution of functional optimization problem (12). Then, we have g*(.) = f"(.). Proof: It is trivial that „ , . p f '(x)- f '(si ) Proof: We have f (s j = lim----------— , i xsi xs i = 1,2,. ...,m. Then there exist 6. > 0 such that for i all x 6 (si -6i, si + <5i) £ Jo1vk(x)g(x) dx-xk k1 0 all > 0 for all g(.) E C[0,1] . By Theorem III.1, we have vk (x )g (x) dx k0 for vk (.) VV where g E = f"(.) fM-A) i - f'(si) < |’ i = 1’2’...’m. (10) on[0,1] .So ^2 J vk(x)f "(x) dx - \ k1 0 0 , hence Now assume that5 = min §.. i = 1,2,...,m . So for i s. e(i—1,±) and x G (s. - <5.,s. + 5.) i mm i ii i ,i = 1,2,...,m the inequality (10) is held. On the other hand, (s. — 5,s. + 6) C (s. — 6 ,s. + 5 ) . Thus by i i i sii si inequality (10) we obtain for all i = 1,2,..., m If -x)-f '(s, )-(x-s,)f "(si )|< fx-sjs j». (11) Thus by integrating both sides of inequality (11) on interval (s^ — <5, s^ + J) , i = 1,2,..., m we can obtain inequality (9).^ Suppose 0 and 0 are two sufficiently small given number and m . For given continuous function f (x) on [0,1] , we define the following functional optimization problem £ Jo v(x)f x) dx-\ k10 <52 Jo v(x)g(x) dx-\ . k1 On the other hand, fH(.) E C2[0,1] which by Theorem III.2 satisfies in constraints of problem (12). Thus, fz'(.) is optimal solution of functional optimization (12).n By Theorem III.2 and solving problem (12), we will obtain the approximate second order derivative of nonsmooth functions. Thus, the GSD of nonsmooth functions will be defined as follows: Definition Ш.5: Let f (.) be a continuous nonsmooth function on interval [0,1] and g*(.) is the optimal solution of the functional optimization problem (12). We denote the GSD of f(.) by GSJ(.) and define as GSdf(.) = g* (.). Remark Ш.6: Note that if f (.) is a smooth function then the GSdf(.) is f/z(.). Also if f(.) is a nonsmooth function then GSD of f(.) is an approximation for second order derivative of f (.). However, the functional optimization problem (12) is an infinite dimensional problem. Thus we will convert this problem to the corresponding finite dimensional problem. For this goal, suppose functions vk(.) E V for k = 1,2,3,...,N as follows: vk (x ) = 1 — cos(2kvrx), k = 1,2,3,..., N (14) where N is a given big number. Thus, the objective function of problem (12) is approximated as the following function: N I(g(•))«£ Jnvk(x)g(x) dx-\. k10 Thus, the objective function of problem (12) can be written as the following which g^,gx,...,gM are the decision variables: hi1hi gi hi2hi gi (17) where gi = g(si), hi, 1 = h(si - 6), hi2 = h(si + 6) and К = h(s^) for all i = 1,2,..., m. Thus, according to the above-mention relations (16) and (17), problem (12) is converted to the following equivalent linear programming problem which Ц 1,щ,...,/iN and их,zi,u,vi for i = 1,2,...,m are unknown variables of the problem: N Minimize 18 k1 subject to -^k+SEvkigik , k = 1,2,..., N i0 , k = 1,2,...,N i0 (ui+vi) + (wi+zi ) u. v. (sq. h h, i = 1,2,...,m i i i i1 ш. — z. + gq. = h.~ — h, i = 1,2,..., m i i ^i i2 i, , ,, u).,z,u,v..Li, > 0, k = 1,2,...,N; i = 1,2,...,m i, i, i, i, ^k , , , , , ,, where Xk for k = 1,2,3,..., N are known parameters by relations (13). Then by solving problem (18), we will obtain the optimal solutions g*0,g*p...,g*m and so by definition III.5 we have GSdf (x^) = g* for all x e [0,1]. IV. Numerical examples In this stage, we find the GSD of smooth and nonsmooth functions in several examples using problem (18). Here we assume e = 6 = 0.01, N = 20, m = 99 and s- = 0.01 i for all i = 1,..., 99 . The problem (18) is solved for functions in these examples using Simplex method in MATLAB software. Attend that in our approach points in [0,1] are selected arbitrarily, and with selection very of these points, we can cover this interval. Thus this is a global approach, while the previous approaches and methods act as locally on a fixed given point in [0,1]. Example IV.1: Consider the smooth function f (x) = ex sin2(x) on interval [0,1]. The function f (x) is illustrated in Fig.1. The exact second derivative of f (x) is shown in Fig.2 and Fig.3 shows the GSD of f (x) which has been obtained by using the problem (18).The absolute error of GSD is presented in Fig.4. Example IV.2: Consider the nonsmooth function f (x) = |2x — 1| on [0,1] . This function is not differentiable in x = 0.5 (see Fig.5) and according to the problem (18), GSD of f (x) has been shown in Fig.6. Example IV.3: Consider the function f(x) = e0.5(x-0.5) sgn(x-0.5) on [0^ 1] . According to Fig.7 (the graph of f (x) ) and Fig.8 (the graph of exact first derivative (FD) of f (x) ), see that f (x) E C1 [0,1] , but f (x) ^ C2 [0,1] . Using problem (18), we calculate the GSD of f (x) which it has been shown in Fig. 9. Fig. 1: The graph of f (x) = ex sin2(x) Fig. 4: The absolute error of GSD of f (x) Fig. 2: The graph of exact second derivative of f (x) Fig. 5: The graph of f (x) 2x — 1 Fig. 3: The graph of GSD of f (x) Fig. 6: The graph of GSD of f (x) Fig. 7: The graph of f (x) = e0'5(x-0'5)2sgn(x"0-5) all of nonsmo- oth optimization problems including problems with nonsmooth objective functions and constraints. We have tested the new approach on some smooth and nonsmooth functions. Preliminary results of numerical experiments show that GSD outperforms other methods considered in this paper. We can conclude that GSD is a good alternative to defining generalized second order derivative. Moreover, in other approaches were defined usually for special functions such as Lipschitz or convex functions while we defined GSD for nonsmooth integrable functions. Acknowledgments Fig. 8: The graph of first derivative of f (x) The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.2. (9)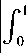
N
Minimize
a 0 ,a1,... aM k=1
m
vg
ki i k
i0
(16)
where v v
ki k
k = 1,2,3,...,N, j
(x ) and
i
= 0,1,..., m ,
gi = g (xi) for
. Moreover, we
approxi- mate the constraints of the problem (12) using simple trapezoidal rule as follows:
Список литературы A New Approach for the Generalized First Derivative and Extension It to the Generalized Second Derivative of Nonsmooth Functions
- H.R.Erfanian, M.H.Noori Skandari and A.V.Kamyad, A numerical approach for nonsmooth ordinary differential equations, Journal of Vibration and Control , forthcoming paper.
- F. H. Clarke, Optimization and Non-smooth Analysis, Wiley, New York, 1983.
- A.D.Ioffe, Nonsmooth analysis: Differential calculus of nondifferentiable mapping, Trans. Amer. Math. Soc. 266(1981), pp. 1–56.
- B.S. Mordukhovich, Generalized differential calculus for nonsmooth and set-valued mappings, J. Math. Anal. Appl. 183(1994), 250–288.
- B. S.Mordukhovich, Variational Analysis and Generalized Differentiation, Vols 1 and 2, Springer, New York, 2006.
- V. Jeyakumar, and D.T.Luc, Nonsmooth vector functions and continuous optimization, Springer, 2008.
- C. Lemarechal and E. Nurminski, Sur la differentiabilite de la fonction d'appui du sous differential approache, C.R. Acad. Sci Paris 290 (1980), 855-858.
- J.-B. Hiriart-Urruty, Approximating a second-order directional derivative for nonsmooth convex functions, SIAM J. Control. Optim. 20 (1982), 381-404.
- J. P. Aubin, Lipschitz behavior of solutions to convex minimization problems, Math. Oper. Res. 9 (1984), 87-111.
- A. Auslender, Stability in mathematical programming with nondifferentiable data, SIAM J. Control. Optim. 22 (1984), 239-254.
- R. W. Chaney, On sufficient conditions in nonsmooth optimization, Math. Oper. Res. 7(1982),463-475.
- A. Ben-Tal, Second order theory for extremum problems. System Analysis and External Methods (A.V. Fiacco and K. Kostaneta, eds.), Lecture Notes in Economics and Mathematical Sciences, Springer-Verlag, 1980, pp. 336-356.
- A. Ben-Tal and J. Zowe, A unified theory of first and second-order conditions for extremum problems in topological vector spaces, Math. Programming Studies 19 (1982), 39-76.
- A. Ben-Tal and J. Zowe , Directional derivatives in nonsmooth optimization, J. Optim. Theory Appl. 47 (1985),483-490.
- R. T. Rockafellar, First and second-order epi-differentiability in nonlinear programming, Trans. Amer. Math. Soc. 307 (1988), 75-108.
- R. Cominetti and R. Correa, A generalized second-order derivative in nonsmooth optimization, SIAM J. Control Optim. 28 (1990), no. 4, 789-809.
- R. T. Rockafellar, Generalized Second Derivatives of Convex Functions and Saddle Functions, Trans. Amer. Math. Soc. 322 (1990).
- A. V. Kamyad, M. H. Noori Skandari and H. R. Erfanian, A new definition for generalized first derivative of nonsmooth functions, Applied Mathematics, 2(2011),1252-1257.


