A New Dual Channel Speech Enhancement Approach Based on Accelerated Particle Swarm Optimization (APSO)

Published Online March 2014 in MECS

The goal of the speech enhancement is to improve the quality and/or intelligibility of the speech degraded by additive noise. The problem of enhancing speech signal which is degraded by additive noise has been widely studied in the past and still an active field of research. Many gradient based algorithms are developed for dual channel speech enhancement. Most commonly used algorithms are the Least Mean Squares (LMS) and Recursive least mean squares (RLS) [1]-[2].

Stochastic optimization based adaptive filtering is an alternative for gradient based algorithms. Nowadays stochastic and heuristic algorithms are becoming powerful for solving the noise reduction problems. These optimization algorithms are independent of system structure and they do not directly affect the parameter update. Particle swarm optimization is one of the recent algorithms in the class of optimization methods [4]. It is inspired by the behavior of swarms of insects, schools of fish, flocks of birds, etc. Several studies are carried out on PSO and there exists almost two dozens of PSO variants [5]. The stochastic optimization technique of PSO has been studied for adaptive filtering [6]. PSO is introduced to speech enhancement application in 2010 by Laleh Badri Asl and Vahid Majid [7]. They also studied an improved particle swarm optimization based speech enhancement algorithm in the same year [8]. Another variant of PSO called asexual reproduction based PSO is studied by L.Badri and M.Geravanchizadeh in 2010 [9]. Hybrid Particle swarm optimization is introduced to speech enhancement in 2010 [10].

Various heuristic approaches have been adopted by researchers for dual channel speech enhancement so far, for example Genetic algorithm [11]-[12], Particle Swarm Optimization and many of the variants of PSO.

These algorithms are based on the concepts found in nature .They have become feasible as a consequence of growing computational power. Some algorithms give a better solution than the others .Hence, searching for new heuristic algorithm for adaptive noise cancellation is an open problem. In standard PSO, initialization of velocities may require extra inputs. A simpler variant is the accelerated particle swarm optimization (APSO) [13], which does not need to use velocity at all and can speed up the convergence in many applications. Hence, in the present paper an attempt has been made to study the effectiveness of APSO optimization technique, in speech enhancement application. This work aims to present the APSO algorithm as a better approach to find more qualitative solutions than SPSO for adaptive noise cancellation.

The rest of the paper is organized as follows; the basic PSO called Standard PSO (SPSO) is explained in section 2. The proposed speech enhancement algorithm is explained in section 3. Section 4 describes the objective measures used for the evaluation of the algorithms, section 5 deals with the simulation results and finally conclusions are given in section 6.

• II.    Review of Particle Swarm Optimization

In the standard PSO [4], all n particles interact and form different trajectories during the search process. Each particle has a position vector, and a velocity vector . The position of the particle represents a possible solution to the optimization. The particles are initially generated randomly in the search space. At each iteration particle moves with two components; a deterministic component and a stochastic component. That is, each particle is attracted toward the position of the current global best g ^* and its own best location x ^* in history, while at the same time it has a tendency to move randomly.

For a particle with position vector x and velocity v its velocity at a new time step is updated as

The phenomenon of linearly decreasing inertia weight was proposed by Shi, as the following equation

(t -1)

^w = ⁽ win ^- wend ) _z⁺ wend             ⁽²⁾

where T is the maximum iterations and t is the current iteration, w and w are the initial and final inertia weights respectively. For many applications, to solve the premature convergence in PSO best values for w and w are set as 0.9 and 0.4.

At a new position during iterations, the position vector of a particle is updated by t+1         t         t+1

x,   = x, + v, At

where A t is the change of iteration. The velocity and position update for a particle in two dimensional search space is shown in Fig.1.

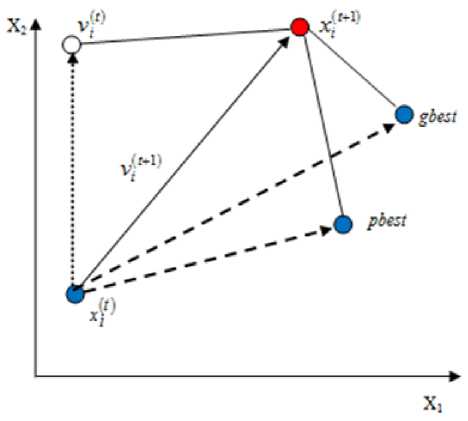
Fig. 1: Illustration of particle movement in 2-dimentional search space t + 1           t      £ v.    = w x v. + a.^

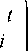
• III.    Proposed Algorithm for Speech Enhancement
  
  3.1    APSO

  + ^^ 2

  
  

  * t ) gi - xi

  
  
  
  

  where ^ and ^ are two random vectors drawn from a uniform distribution [0,1]. Here a and в are called the learning parameters or acceleration coefficients, and w is the inertia weight, used to maintain the momentum of the particle.

  
  

  The movement of a swarming particle consists of two major components: a stochastic component and a deterministic component. Each particle is attracted towards the position of the current global best g ^* and its own best location x ^* in history, while at the same time it has a tendency to move randomly. There is a current best for all n particles at any time t during iterations. The standard particle swarm optimization uses both the current global best g ^* and the individual

  
  

best x ^* to update the particle position. The reason for using the individual best is to increase the diversity in the search space. However, this diversity can be achieved by using some randomness. Subsequently, there is no compelling reason for using the individual best, unless the optimization problem of interest is highly nonlinear and multimodal.

A simplified version which could accelerate the convergence of the algorithm is to use the global best only. Thus, in the APSO, the velocity vector at iteration t + 1 is generated by a simpler formula [4]

t+1      t                 * t

vi = vi + a^n + P\g - xi )

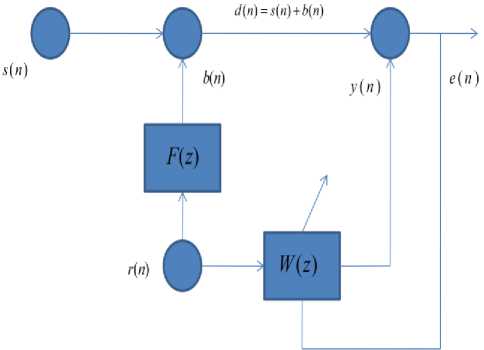
Fig. 2: Block diagram of dual channel speech enhancement system

where ^ is a random vector in the interval of {0,1}.

The update equation for position vector is simply

t+1      t     t+1

x^    = x^ + V •

The rate of convergence of algorithm can further be increased by updating the location of particle in a single step as follows

xit+1 =(1 - в)xi + вg * + a^n

The typical values for APSO are α from 0.1 to 0.4 and β from 0.1 to 0.7, though α = 0.2 and β = 0.5 can be taken as the initial values for most unimodal objective functions. It is worth pointing out that the parameters α and β should in general be related to the scales of the independent variables and the search domain [14].

• 3.2    APSO to Speech Enhancement

The structure of the Dual channel speech enhancement system is shown in Fig.2. In dual channel speech enhancement, it is assumed that noisy speech signal 5 ( n ) is present in one channel and the reference noise signal r ( n ) is present in the second channel. F ( z ) is the acoustic path between these two signals. The transfer function F ( z ) of the acoustic path is derived by using an adaptive filter W ( z ) . In the present paper, the adaptive filter W ( z ) is modeled using the APSO algorithm.

Most of the nonlinear systems are recursive in nature. Hence models for real world systems are better represented as IIR systems. Based on this consideration, for our practical simulation, we model an IIR filter as an acoustic path between the two channels of a dual channel enhancement system.

An infinite impulse response (IIR) filter is a recursive filter in which the present output depends on previous outputs. The difference equation of IIR filter is shown below:

LM

y (n) = УaiX(n -i)—Уbiy (n -i)       (7)

i = 0                       i = 1

where a and b are the coefficients of the filter and M ( > L ) represents the order of the filter.

The transfer function of the M ^th order IIR filter is given as

L

/ x У a,z -H (z ) = Az) =    ----

M

B(z)  1+У biz i =1

The primary input signal of the dual channel system d ( n ) which consists of clean speech signal and noise signal b ( n ) is made available to the adaptive filter. The characteristics of the adaptive filter are then modified so that the output of the filter y ( n ) resembles d ( n ) as close as possible.

The main complication which IIR filters introduce is that they depend nonlinearly on their coefficients .This can be overcome by applying an optimization technique such as Particle swarm Optimization (PSO) or Accelerated PSO (APSO).

Using optimization technique several possible collections of IIR coefficients are chosen and could see what error each produces. Based on those results, new points are chosen to test, and continue until all of the points have clustered together and swarm in a small area.

Input speech signals are segmented into frames. In stochastic optimization based speech enhancement it is required to define an objective function to evaluate the fitness of each particle. Here, the objective function is defined as the average error between the noisy speech and estimated noise signal in each frame. The expression for the fitness function J is given as

J.=

where

of filter

N ²

- £(d (k) - уД k )) L k=0

L is length of frame and y ( n ) is the output

W(z) for it agent. Here W(z) is designed by using APSO. Each particle in the swarm is considered as a candidate solution which represents a set of coefficients of adaptive filter W(z).

After some iterations, W ( z ) gives the best solution when the fitness value is minimum i.e. J is minimum. The noisy signal y ( n ) is estimated by convolving the noise reference r ( n ) with the error signal. Then enhanced frame is obtained by subtracting the estimated noise signal from noisy speech.

To implement the APSO in speech enhancement application, it is required to set some parameters. They are number of iterations ( t ), number of particles

( n ) and acceleration constants given in (6).Flow chart for APSO is given in Fig.3.

Step 1 . Create a population of particles; here each particle is a set of coefficients of adaptivefilter W ( z ) •

Step 2 . Evaluate the objective function for each particle position by using equation (9)

Step 3 . Find the current best location

Step 4 . Move the particles into new locations according to the equation (6)

Step 5 . Go to step 2 until stop criteria satisfied

• IV.    Objective Measures

• 4.1    SNR

The objective measures that are considered for the evaluation of the proposed algorithm are Signal to Noise Ratio (SNR), Perceptual Speech Quality Measure (PESQ) and Fractional Articulation Index (FAI).

SNR is the most common measure of performance that has often been used to evaluate the enhancement algorithms. SNR is defined as [16]

Start

Set number of iterations, no of particles, a and в

Fig. 3: Flow chart of APSO

X x ² ( n ) E ^{( x ( n ) -} y ^{( n )) 2}

S/N = ^10log

where X(n) is the clean speech and y(n) is the distorted speech.

The difference between the SNR of enhanced speech and that of noisy speech is the measure of the Improved SNR (SNRI).

SNR of enhanced speech signal is calculated by equation (10).

• 4.2    PESQ

• 4.3    FAI

To compute the PESQ measure, first the clean signal and the degraded signals are level equalized to a standard listening level and these signals are allowed through a filter having the response similar to a standard telephone handset. The time delays are corrected by aligning the signals and processing through an auditory transform like BSD to obtain the loudness spectra. The difference in the loudness spectra of clean signal and degraded signal is computed and averaged over time and frequency and is termed as disturbance [15]-16]. As in Hu and P.Loizou [17], PESQ score is computed as a linear combination of the average disturbance value D and the average asymmetrical disturbance values A and is given by

PESQ = 4.5 - a 1 D ind - a 2 A ind            (11)

where a = - 0.1 and a = - 0.0309

PESQ score ranges from 0.5 to 4.5. Higher values represent better quality according to the ITU-T Recommendations P.862 standard.

This measure is based on the principle that the intelligibility of speech depends on the proportion of spectral information that is audible to the listener and is computed by dividing the spectrum into 20 bands (contributing equally to intelligibility) and estimating the weighted average of the signal-to-noise ratios (SNRs) in each band. FAI is computed based on the weighted average of the proportion of the input SNR transmitted by the noise-suppression algorithm [18] in each band and is given by

M

FAI = _M ¹   ∑ W k × fSNR k          (12)

_{∑ Wk} k = 1 k = 1

where W denotes the weighting functions or bandimportance functions applied to band k and M is the total number of bands used and fSNR denotes the fraction of the input SNR transmitted by the noise reduction algorithm

0                   10                  20                   30                   40                  50                   60                  70                   80

Iterations

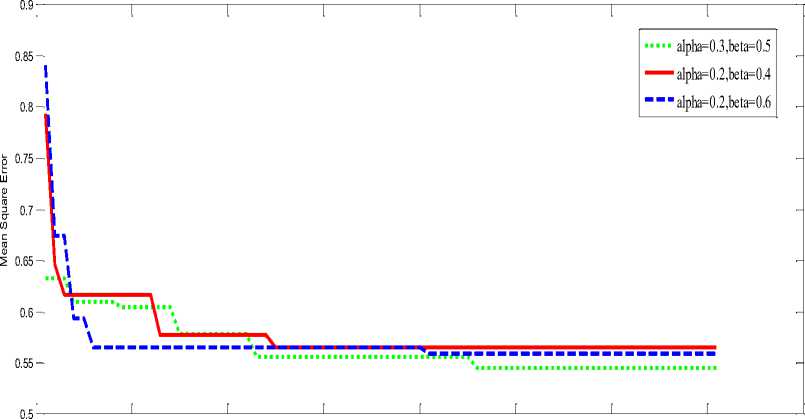
Fig. 4: Effect of acceleration coefficients on APSO

Table 1: Simulation parameters for SPSO

Algorithm	Parameter	Value
	N	30
	Iterations	70
	α	0.5
SPSO	β	0.5
	win	0.9
	wend	0.4
	Samples for each frame	320

Table 2: Experimental conditions for APSO

Algorithm	Parameter	Value
	n p	30
	t max	70
APSO	a	0.3
	в	0.5
	Samples for each frame	320

APSO than SPSO. Time domain waveforms of noisy speech, clean speech and the speech signals enhanced by APSO and SPSO are shown in Fig.6. From these waveforms it can be clearly noticed that the signal enhanced using APSO algorithm resembles close to the clean speech compared to the signal enhanced by SPSO. The performance of the proposed algorithm is also studied in terms of intelligibility by evaluating the objective measure called FAI. Graphical representations for the improvement in objective measures SNRI, PESQ and FAI for babble noise condition are shown in Fig.7 and Fig.8 and Fig.9 respectively. Results indicate that the intelligibility of speech enhanced by APSO is better than the signal enhanced by SPSO.

Five clean speech sentences are selected randomly from NOIZEUS database [19] for the simulation. Noise references are taken from the NOISEX-92 database [20]. The noisy speech signal is obtained by adding the clean speech signal to the noise reference modified by a transfer function F (z). So, F (z) is the acoustic path between the two input signals.

The filter F(z) used in our simulation is a second order IIR filter and is defined as follow

F ( z-1) =

1

1 -1.2 z -1 + 0.36 z’2

The adaptive filter W ( z ) is given as

W' (z-1) =

^p 1 ⁱ

1 + p\z -1 + p'z ”2

where p ⁱ is the j ^th dimension of i ^th agent in the swarm.

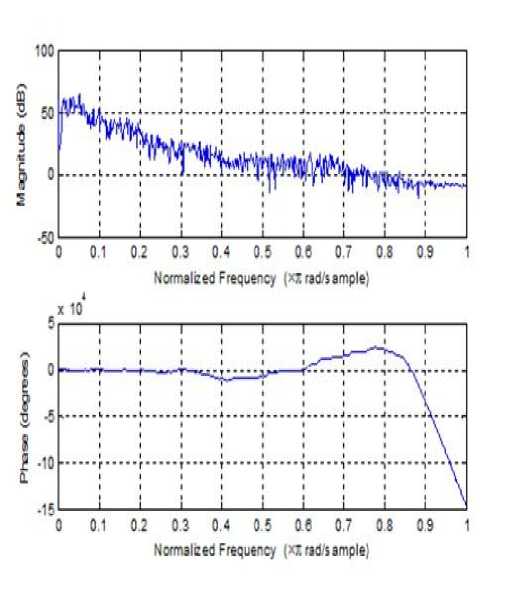
Fig. 5: Magnitude and frequency response of acoustic path

The stochastic optimization algorithm called APSO Algorithm is used to determine the weights of the adaptive filter W ( z ) .The input noisy signals are segmented into frames of 20ms. Each frame consists of 320 samples. The simulation parameters chosen for APSO and SPSO are shown in Table 1 and Table 2 respectively. The effect of different acceleration coefficients on convergence of APSO is shown in Fig.4. From this figure it is observed that acceleration coefficients of a = 0.3 and в = 0.5 gives the better solutions for our problem. Magnitude response of acoustic path is shown in Fig.5.The SNR levels of the input noisy signal for babble and factory type noise is set at -10, 0 and 5dB. Results are averaged over 10 trail runs. Table 3 gives the comparison for the SPSO algorithm and APSO using an objective measure called improved SNR (SNRI) in babble noise condition. Results show that SNRI is significantly improved for

Table 3: Improved SNR of APSO and SPSO

Input SNR for babble Noise(dB)	Algorithm	Improvement in SNR (dB)
5	SPSO	6.06
	APSO	9.31
0	SPSO	8.02
	APSO	12.17
-10	SPSO	22.26
	APSO	25.25

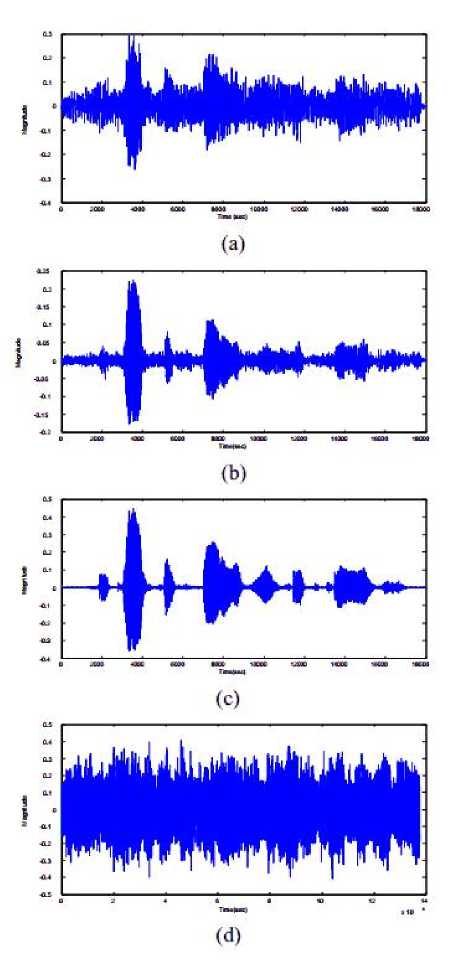
Fig.

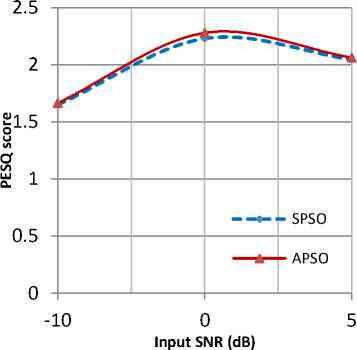
Fig. 8: Graphical representation of improvement in PESQ score for babble noise input

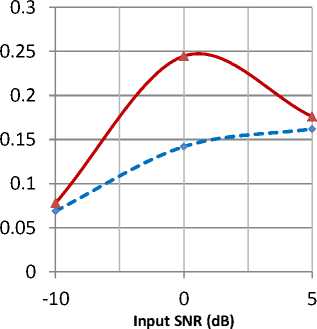
Fig. 9: Graphical representation of improvement in FAI measure for babble input noise

Improved SNR(dB)

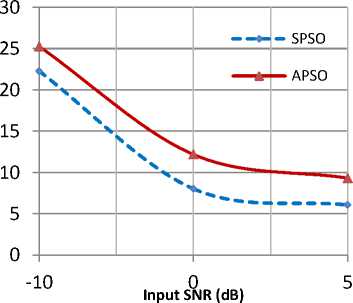
Fig. 7: Graphical representation of improved SNR under babble noise condition

Table 4: Evaluation of algorithms in factory noise condition

Input SNR for Factory Noise(dB)	Algorithm	SNR	FAI value	PESQ score
	SPSO	3.8736	0.1213	1.8815
5	APSO	4.0353	0.1315	1.9205
	SPSO	2.8716	0.0773	1.6687
0	APSO	3.8654	0.0833	2.1307
	SPSO	-3.6818	0.0280	1.6999
-10	APSO	-2.8266	0.0313	1.7628

Iterations

• Fig. 10: Convergence of MSE for APSO and SPSO

  

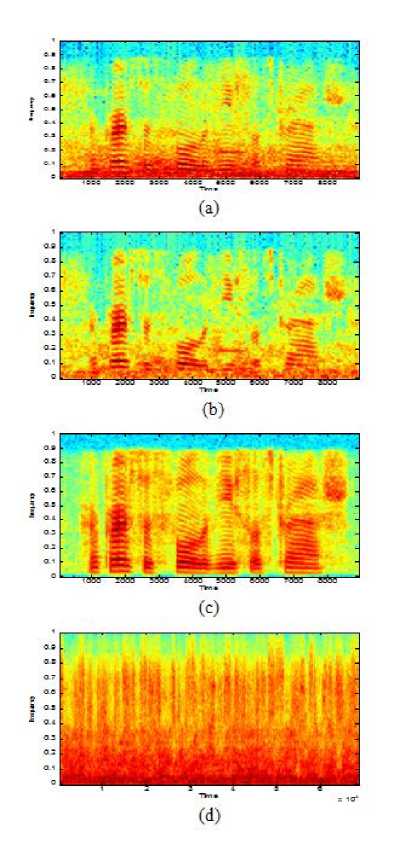
  Fig. 11: Spectrograms of (a) signal enhanced by SPSO (b) Enhanced signal of APSO (c) Clean speech and (d) Babble noise reference signal

  
  

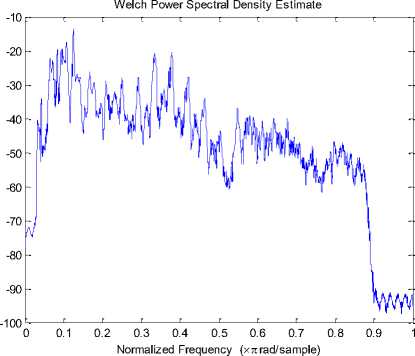
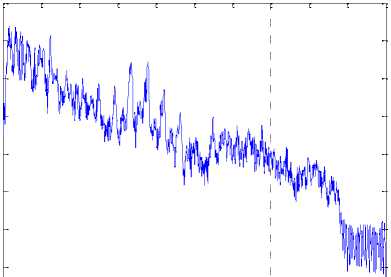
The objective measures are computed by segmenting the sentences using 30-ms duration Hamming window with 75% overlap between adjacent frames. The convergence of SPSO and APSO algorithm is shown in Fig 10. From this figure, it can be clearly noticed that APSO finds more qualitative solution than SPSO with minimum fitness value (minimum mean square error for APSO). The spectrograms for speech signals are shown in Fig.11. The power spectral densities of the signals enhanced by APSO and SPSO are compared in Fig.12. From this figure it can be inferred that the signal estimated with APSO based approach is close to clean speech when compared with the SPSO based approach. Table 4 shows the performance evaluation of both the algorithms under factory noise condition. From this table it can be clearly observed that APSO speech enhancement algorithm outperforms than the SPSO based enhancement algorithm.

• VI. Concluding Remarks

This paper deals with the problem of adaptive noise cancellation in speech enhancement using stochastic and heuristic optimization strategies. In this present work, a recently developed stochastic and heuristic optimization algorithm called Accelerated particle Swarm Optimization (APSO) is introduced to speech enhancement application. Its performance is compared with another approach which is based on the well known heuristic algorithm called Standard PSO algorithm. From the simulation results (Tables 3 and 4) it can be concluded that the performance of APSO algorithm is better when compared to SPSO with respect to the speech quality and intelligibility, as there is an improvement in the corresponding objective measures SNR, PESQ and FAI values.

Power/frequency (dB/rad/sample)                                                  Power/frequency (dB/rad/sample)

(a) Clean

From the convergence analysis of SPSO and APSO (Fig.10) it is noticed that APSO has faster convergence than SPSO and could find the best quality solution for adaptive filter coefficients in our problem of active noise control. Hence, APSO may effectively enhance the noisy speech by improving the quality of speech compared to the existing SPSO based speech enhancement. It can also be concluded that APSO could reduce the back ground noise distortion more effectively than SPSO, as it has improved intelligibility and PESQ scores.

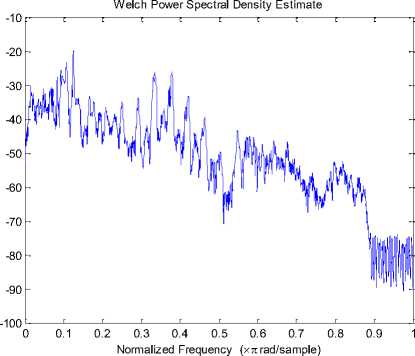
(b) APSO

Welch Power Spectral Density Estimate

-10

-20

-30

-40

-50

-60

-70

-80

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Normalized Frequency ( хп rad/sample)

-90

(c ) SPSO

Fig. 12: Comparison for the power spectral densities of (a) the clean speech, signals enhanced by (a) APSO and (b) SPSO at -10dB input SNR

• [1]    B. Widrow, and S. Stearns, Adaptive Signal Processing , Englewood Cliffs, NJ: Prentice Hall, 1985

• [2]    T.Ueda, H suzuki, Performance of Equalizers Employing a Re-training RLS Algorithm for digital mobile radio communications , 40 th IEEE Vehicular Technology Conference, 1990, pp 553558

• [3]    P.Mars, J.R.Chen, and R. Nambiar, Learning algorithms: theory and applications in signal processing, control and communications, CRC Press, Boca Raton, FL, 1996

• [4]    R.C.Eberhart, and J.Kennady, A new optimizer using particles swarm theory,Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, IEEE Press, Piscataway,NJ,1995, pp.39-43.

• [5]    Krusicnski, D.J. and Jenkins, W.K., Adaptive Filtering Via Particle Swarm Optimization,” Proceedings of 37^th Asilomar Conf on Signals, Systems, and Computers, November 2003.

• [6]    D. J. Krusienski and W. K. Jenkins, Design and Performance of Adaptive Systems Based on Structured Stochastic Optimization Strategies, Circuits and Systems Magazine, Vol. 5, No. 1, 2005, pp 8 –20.

• [7]    Laleh Badri Asl and Vahid Majid Nezhad, Speech enhancement using Particle swarm optimization Techniques, International conference on Measuring Technology and Mechatronics Automation, 2010, pp 441-444.

• [8]    Laleh Badri Asl and Vahid Mjid Nezhad, “Improved Particle Swarm Optimization for DualChannel Speech Enhancement”, International Conference on Signal Acquisition and Processing, 2010, pp 13-17.

• [9]    L.Badri Asl and M.Geravanchizadeh, Asexual Reproduction based adaptive quantum particle swarm optimization algorithm for dual channel speech enhancement , International conference on

  Information science, Signal Processing and their Applications, ISSPA, 2010 , pp 129-132.

• [10]    Sina Ghalami Osgouei, and Masoud Geravan Chizadeh, Dual –Channel Speech Enhancement based on a Hybrid Particle Swarm Optimization Algorithm, 5th International Symposium on Telecommunications (IST’ 2010), pp.873-877.

• [11]    White, M.S. and Flockton,S.J., Chapter in Evolutionary Algorithms in Engineering applications, Springer Verlog, 1997, pp.361-376

• [12]    Kumon, T.Iwasaki, M.,Suzuki, T.Hashiyama, T.;Matsui,N., Okuma,S., Nonlinear system identification using Genetic Algorithm Industrial Electronics Society, IECON 2000. 26^th Annual conference of the IEEE- volume 4, 22-28 Oct. 2000, pp. 2485- 2491 Vol.4.

• [13]    X.S.Yang, Nature-Inspired         Metaheuristic

  Algorithms, Luniver Press, 2nd edition, 2010.

• [14]    Yang, X. S., Deb, S., and Fong, S., Accelerated Particle Swarm Optimization and Support Vector Machine for Business Optimization and Applications, in:   NDT2011, CCIS 136,

  Springer,2011, pp. 53-66

• [15]    A.Rix, J. Beerens,M.Hollier and A. Hekstra, Perceptual evaluation of speech quality (PESQ) -A new method for speech quality assessment of telephone networks and codecs , in Proc. IEEE, Int. Conf. Acoustics Speech, Signal processing, 2001;vol.2, pp 749-752.

• [16]    Philipos C.Loizou, Speech Enhancement Theory and Practice, CRC press.2007

• [17]    Y.Hu and P.Loizou, Subjective comparison of speech enhancement algorithms, ICASSP Proceedings. Toulouse, Franc., 2006, pp 153-156.

• [18]    Philipos C. Loizou and Jianfen Ma, Extending the articulation index to account for non-linear distortions introduced by noise- suppression algorithms, J. Acoustic Society of America, 2011, pp 986-995.

• [19]     http://www.utdallas.edu/~loizou/speech/noizeus

• [20]     http://www.speech.cs.cmu.edu/comp.speech/Sectio n1/Data/noisex.html

  Authors Profiles

  
  
  

  K.Prajna received the B.Tech degree in ECE from Pragati Engineering College and M.Tech degree in Radar and Microwave Engineering from Andhra University in 2009. She is currently pursing Ph.D in the Department of ECE Andhra University, Visakhapatnam, India.

Her area of research interests includes signal processing, speech processing and intelligent systems.

Dr. G. Sasi Bhushana Rao is presently working as a Professor and Head of the Department in Dept. of Electronics and Communication Engineering, Andhra University College of Engineering. He has 28 years of experience in Industry, Research and Teaching. He has 290 research publications in National and International Conferences and Journals. He is a recipient of “Dr. Survepalli Radhakrishnan Best Academician” of the year 2008, and best researcher award in the year of 2007 from Andhra University, Visakhapatnam.

Dr. K.V.V.S. Reddy is a former Professor of Electronics and Communication Engineering in Andhra University College of Engineering. He has published more than 70 journal and conference papers. He has 33 years of experience in teaching and research besides possessing 3 years of industrial experience. He is a

Fellow of Institute of Electronics and

Vignan’s Institute

R.Uma Maheswari received the B.Tech degree in ECE from MVGR college of Engineering and the M.Tech degree in VLSI System Design from Avanthi Institute of Engineering & Technology, in 2012. Presently Working as Assistant Professor in of Information Technology,

Visakhapatnam. Previously, she worked as Assistant Professor in Avanthi College of Engineering, which is affiliated to JNTU. She worked as IT- Associate in IEG