A New Dynamic Data Cleaning Technique for Improving Incomplete Dataset Consistency

Data cleaning is a pre-processing technique to improve the accuracy of the data analysis system by identifying, removing and reconstructing abnormal data objects in the existing dataset or database [1-3]. Typical data errors occur due to the misuse of abbreviations, data entry mistakes, duplicate records, missing values, spelling errors and outdated codes which can directly affect the data analysis results in various field applications like Data Mining, Data Warehousing, Image Processing, Machine Learning, Bioinformatics and Biomedical [4]. Presently the trend in the data cleaning research includes duplicate detection, missing attribute value detection, missing value modification, outlier detection, logical confusion detection and redundant data processing [5].

Identifying and reconstructing the missed attribute value in the inconsistent data objects or records in incomplete dataset is an important task in the data cleaning technique [6]. Generally, the missing data problem in incomplete dataset is classified into three classes: Missing Completely At Random (MCAR), missing At Random (MAR) and Missing Not At Random (MNAR). Many authors have suggested major that the issue in existing data cleaning techniques is that they follow an approximation statistical procedure to reconstruct the missed data value in the inconsistent data object by randomly selecting neighborhood object or randomly defining the missed data value through the user. To overcome this, in this paper, a new Dynamic Data Cleaning scheme is proposed to improve the dataset consistency through following steps:

• 1)    Identifying normal objects and outliers (abnormal object) based on the degree of missing attributes

• 2)    Removing outliers and reconstructing missed attributes in normal objects by closest objects based on the distance metric without user input

• 3)    Estimating the dataset quality based on object consistency and inconsistency measures.

This paper is organized as follows: related work is discussed in Section II. Section III contains details of the proposed approach. The dataset quality measure and complexity analysis are discussed in sections IV and V respectively. Finally, the Experimental results and performance measures are discussed in Section VI. Conclusions and scope for further research are drawn in Section VII.

• II.    Related Work

Several data cleaning techniques have been reported in the past [7-11] namely Imputation, Partial Imputation, Partial Deletion, Full Analysis and interpolation which used to handle missing data problem in inconsistent dataset or incomplete database. The two standard techniques like Expectoration Maximization (EM) and likelihood optimization with gradient method were described in [12-14]. These two techniques are intended for estimating the parameters of Bayesian network and subsequently they solve the data missing at random (MAR) problem in inconsistent dataset or incomplete dataset. The performance of these techniques is limited by many factors: (i) they are following iterative procedure, (ii) they need inference of a Bayesian network to estimate parameters and (iii) they are immovable in local optima. Mohan et al. [15] designed a non-iterative with closed form approach to estimate consistent parameters for missing data errors like MCAR, MAR and MNAR in incomplete dataset without inference of a Bayesian network.

Another technique called Multiple Imputation (MI) was discussed in [16-18] to reconstruct the single missed value by multiple values with multiple times in incomplete dataset. This technique follows three phases to reconstruct the missed value in inconsistent object or instance in incomplete dataset. First phase, it replaces each missing value with a set of m reasonable values that represent the improbability nearly the right value to impute and subsequently it generates m imputed complete datasets, where m denotes the number of times. In the next phase, it analysis m imputed complete datasets by using standard statistical procedures. Finally, the results of m analysis from the m imputed complete datasets are combined to produce inferential results without missed data.

The authors Mirkes et al. in [21] have designed a data preprocessing system of non-stationary Markov models which used to handle missed data in inconsistent healthcare dataset. Another method called Full Information Maximum Likelihood was reported by many authors in [19-20]. This FIML method is aimed to reconstruct the missed data in incomplete dataset by statistical model such as structured equation model or growth model without the misleading resulting from the imputed values. The FIML method could estimate the population parameters to construct the analysis model based on the available information in incomplete dataset, where finding the parameter values that exploit the possibility of making the available information given the parameters. In [23], the authors Melissa et al. were presented an imputation scheme called Multiple Imputation Chained Equation (MICE). The MICE scheme is intended to reconstruct the missing data in the incomplete dataset. The authors suggested that the MICE scheme could not have same theoretical justification compare to other existing imputation techniques.

Bukola et al. (2017) [24] presented another preprocessing scheme to improve the data quality in web server log file. This scheme is aimed to reconstruct the data quality over the university web server log file by identifying and removing the intrusion data from file. They suggested the pre-processing scheme is processing the log file through four stages including Data Conversion, Session Identification, Data Cleaning and Data Discretization. Another pre-processing scheme was reported by Sameer and Navjot in [25] to improve the quality of small dataset. This pre-processing scheme uses the improved fuzzy technique that used to reconstruct the inconsistent small dataset into consistent dataset. The authors claimed that the pre-processing scheme is well supported to improve the data classifier accuracy.

In [26] the authors Kavithakumar and chadrasekaran presented two different algorithms namely Context Dependent Attribute Correction and Context Independent Attribute Correction to reconstruct the attribute quality in inconsistent dataset without user input. The first method Context Dependent Correction is used to reconstruct the inconsistent attribute value in record based on association rules. Similarly, the Context Independent Correction method aimed to correct the unreliable attribute value in inconsistent record based on clustering technique. They suggested that the Context Dependent Correction is produced better result than Context Independent Correction without external reference data point. Anosh et al. (2017) [27] reported a survey of data preprocessing techniques and tools. They estimated the performance of many data pre-processing techniques and tools (YALE, ALTERYX and WEKA) through testing over the different datasets. The authors suggested and determined through the experimentation results, that the pre-processing technique is better suitable to improve the data consistency in data warehouse by cleansing, standardizing, correction, matching and transformation respectively. A brief discussion of the steps involved in the proposed DDC technique is presented in the next section.

• III.    Proposed Dynamic Data Cleaning

In this section, detail of the proposed Dynamic Data Cleaning approach is presented. The proposed approach contains three stages. In the first stage, the INO process divides a dataset into normal objects and irregular objects based on degree of missing attributes in each individual object in the dataset. In the second stage, the proposed approach removes the abnormal objects (outlier) with high degree of missing attributes and reconstructs the normal objects with lesser number of missing attributes based on the RNO method. Finally, the proposed DDC approach estimates the object consistency and inconsistency over the improved dataset, based on the DQM scheme. The stages are involved in the DDC approach is illustrated in Fig. 1 and the methods are described in the subsections below.

• A.    Identify Normal Object

INO identifies normal and abnormal objects over incomplete dataset by tracing the degree of missing attribute values in each individual object. It consists of three steps. The first step, it computes the degree of missing attributes ( DM ) over each individual object in the incomplete dataset X = x _i for i = 0,1,2,.., n , where n denotes the size of the dataset X and is defined in the equation (1) as:

nN

DM _i

=EZ xj

i = 0 j = 0

V x ij e x i , V x i e X

[          [ 1     Y.. ■

,  I             I 1     xij and < x» = < „

[ ^j    [ 0   X ij *

D r ( C 1 k , C 1 )

m N EZ d Cw ' r = 0 j = 0

V C 1 rj e C 1 r , C 1 r e C i ,

^V C i kj ^e C i k ^and C i ^{e X}

where x _ij denotes the j ^th attribute value in the i ^th object belonging to the dataset X , N describes the number of attributes in the object for j = 0,1,.., N , x ij = ? represents the condition which describes that the j ^th attribute value is missed in the i ^th object of incomplete dataset X , x ij * ? denotes the condition of j^tth attribute value in the i ^th object is not missed and n represents the size of the dataset X for i = 0,1,.., n . In the second step, it confirms if the object is consistent or inconsistent through the degree of missing attributes of each object DM _i in the three cases:

• 1)    If the degree of missing attributes in the i ^th object does not exceed the threshold value zero ( DM i = 0) it then confirms that the i ^th object is normal with a high consistency.

• 2)    If the degree of missing attributes in the i ^th object DM _i is not equal to zero and does not exceed the threshold ( DM i >  0&& DM i <  3) then it means that the i ^th object is normal and needs to be reconstructed with its missing attributes values.

• 3)    If the degree of missing attributes of the object DM i exceeds the threshold ( DM i >  3) it then confirms that the i ^th object is an abnormal (outlier) and it has to be ignored.

Based on the above three cases, the incomplete dataset X is partitioned into two clusters namely C 1 , and C 2 through degree of missed attributes or data in the objects. The first cluster C₁ contains consistent objects with 0 to 2 degree missed attributes data. The second cluster C₂ contains inconsistent objects (outliers) with above three degree missed attributes values. However, the threshold (limited number of missed attributes data) range is not constant in the proposed DDC approach and it disagrees among the incomplete datasets based on the number of attributes.

• B.    Reconstruct Normal Object

The RNO method aims to reconstruct the missed attribute values in normal objects based on its closest object. It consists of three steps. In the first step, it identifies the object with missed attributes data. In the next step, it finds the closest object with a higher similarity of object with the missed attributes in the same cluster based on the Euclidean distance metric D _{( C , C )} as defined in the equation (2) given below:

where m represents the number of normal objects or size of the cluster C ₁ for r = 0,1,2,.., m , r describes the r^th object in C ₁ , d ( C _{1 kj} , C _{1 rj} ) denotes the Euclidean distance between k^th and r^th objects in C ₁ and is defined in the equation (3) as:

d ( C i _kj , C i rj ) = [ ( C i k - C i rj ) 2 ]/2                (3)

where, C _{1 kj} denotes the j^th attribute value in k^th object that belongs to the C ₁ , C _{1 rj} represents the j^th attribute value in r^th object in C . In the last step, it reconstructs the objects with missed attributes by its closest object with a higher similarity that belongs to the C ₁ cluster in X and the algorithm is described hereunder.

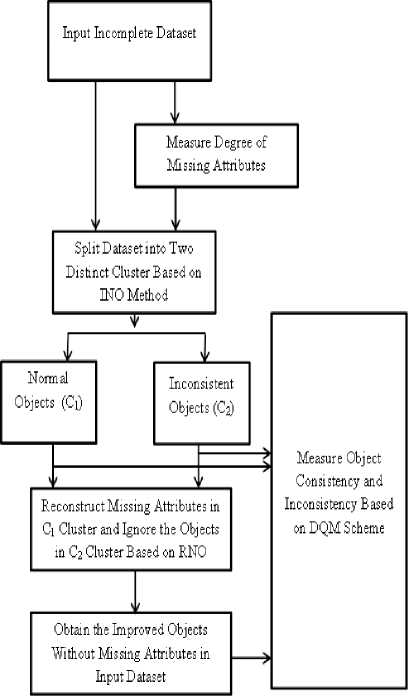
Fig.1. Functional Diagram of DDC Approach

• C.    Algorithm

Input: Incomplete Dataset X Containing n Objects { x ₀, x ₁,.., x _n }

Output: Complete Dataset X Containing m Objects Begin

• 1.    Measure the degree of missed attributes DM _i over each individual data object in   X = x ij for

• 2.    Split the dataset X into two clusters C ₁ (normal objects) and C ₂ (outliers) based on the degree of missed attributes as described in subsection III.A.

• 3.    Reconstruct the normal data objects with missed attributes in cluster C ₁ by its closest data object within the same cluster for r = 0,1,2,.., m as expressed in subsection III.B.

• 4.    Remove the incomplete data objects with higher degree of missed attributes values in C ₂ and update the dataset X

• 5.    Modify the dataset X with reconstructed normal objects results.

i = 1,2,.., n , j = 1,2,.., N as described in Equation (1)

End attributes in the ith object in dataset X , x represents the jth attribute in ith object that belongs to X , N denotes the number of attributes, n describes the size of dataset X and

Zxi ^ 1 describes the condition of sum of number of missed attributes values in ith object which is higher or equal to one.

• B. Object Consistency Measure

The OCM method measures the objects consistency over the dataset X through the process of tracing the missed attributes in each individual object for i = 0,1,..,n , where X denotes the dataset and n represents the size of the dataset X and is defined in the equation (6) as:

Г NCO

OCM ( X ) = ^ NCO x 100

I n

where, NCO denotes the number of inconsistency objects which belong to the dataset X . The notation NCO is computed by tracing the objects without the missing attributes over the dataset X and is computed by

• IV.    Dataset Quality Measure Stage

This stage presents a new technique called Dataset Quality Measure (DQM). The proposed technique aims to estimate the quality of the dataset by measuring the consistency and inconsistency over objects in the dataset. It consists of two measures: Object Inconsistency Measure (OIM) and Object Consistency Measure (OCM). The measures are described in the subsections below.

NCO = ^

N where Z Xij

nN

ZZ Xj

i = 0 j = 0

where <  0

y..    9

x j * .

x ij =

Z x = ^N.

denotes the count of non-missed attributes

• A. Object Inconsistency Measure

This OIM method measures the inconsistency over dataset X by tracing the missing attributes in each individual object for i = 0,1,..,n , where X denotes the data set, n represents the size of the dataset X and is defined in the equation (4) as:

in the i^th object in the dataset X , x represents the j^th

attribute in i^th object that belongs to the X ,

Z x i = ^N

OIM ( X ) = ] NO x 100 I n

describes the condition of sum of number of non-missed attributes values in i^th object which is equal to N , n denotes the size of the dataset X and N represents the number of attributes.

where NIO denotes the number of inconsistency objects in the dataset X . Next, the notation NIO is computed through tracing the missed attributes over the each individual object in X and is defined in the equation (5) as:

NIO = ^

nN

ZZx.

i = 0 j = 0

where <  1

x j * ?

x ij = ? l

2 x ^ 1

where

N

Z x ij

denotes the sum of number of missed

• V.    Complexity Analysis

This section discusses in detail the computational complexity of the proposed DDC scheme. The INO method requires time O ( nN + n ) to measure the degree of missed attributes over each individual object in dataset X and split the dataset into two groups normal objects and outliers respectively, where n represents the number of objects in dataset X = x i for i = 0,1,2,.., n and N denotes the number of attributes in object x _i = x _ij for j = 0,1,2,.., N . The RNO method in the proposed scheme consumes time O ( kmN ) to reconstruct normal objects with missed attributes values by its closest normal object, where k represents the number of normal objects with missed attributes values have been reconstructed, m denotes the number of normal objects in the dataset X .

Next, the DQM scheme requires time O ( mN ) and O ( nN ) to estimate the consistency and inconsistency over the dataset without and with outliers, respectively. Overall, the proposed DDC technique requires time O ( nN + n + kmN + mN) to trace inconsistent data objects and to improve the dataset consistency.

• VI.    Results and Discussions

The proposed Dynamic Data Cleaning (DDC) approach is experimented on 100 incomplete UCI datasets with different size as presented in this section. A subset of the inconsistent dataset containing six UCI sample incomplete datasets [22] including Mamographics_Masses, Deematology, Heart_dises1, Heart_dises2, Heart_dises3 and Horse_Colic including its size and number of attributes are presented in Table1.

Table 1. Sample Incomplete UCI Datasets

UCI dataset ( x )	Dataset Size ( n )	Number of Attributes ( N )
Mamographics Masses	961	06
Deematology	366	35
Heart_dises1	304	14
Heart_dises2	294	14
Heart_dises3	123	14
Horse_Colic	306	28

Initially, the proposed DDC approach estimates the level of consistency (OCM) and inconsistency (OIM) in % among the objects in the incomplete dataset based on DQM scheme as described in section IV. The count of objects with missing attributes (NIO) and objects without missing attributes (NCO) are estimated on seven UCI datasets Mamographics_Masses, Deematology, Heart_dises1, Heart_dises2, Heart_dises3 and Horse_Colic, respectively and the results are presented in Table 2. Then, the level of consistency OCM and inconsistency OIM are measured in % on the UCI datasets and the results are 83.36, 97.81, 98.01, 0.340, 2.0, 2.0 and 13.63, 2.187, 1.98, 99.65, 99.18, 98.0 respectively. The measured results are incorporated in Table 3. It is clearly noticed from Table 3, that the first three UCI datasets associate with higher consistency and lesser inconsistency objects; likewise, the second three datasets also associate with lower consistency and higher inconsistency objects. Fig 2 shows the level of consistency and inconsistency of the incomplete UCI datasets which presented in Table 3.

Next, the proposed DDC approach is traced the normal objects and outliers on datasets as described in the subsection III.A and similarly the process of reconstruction of normal objects with missing attributes on datasets as defined in subsection III.B. The experiment on seven UCI datasets including Mamographics_Masses, Deematology, Heart_dises1, Heart_dises2, Heart_dises3 and Horse_Colic are described below.

Mamographics_Masses: This dataset contains 961 objects with six attributes. First, the INO method identified 830 normal objects with zero degree missed attribute, 101 normal objects with lesser degree of missed attributes and 30 abnormal objects with a higher degree of missing attributes data respectively over the dataset and these results are presented in Table 4. Subsequently, the RNO method reassembled the missed attributes in the 101 normal objects by its closest objects and this modified dataset is given in Table 5.

Table 2. Results of Objects with Missed Data and Objects without Missed Data on UCI Incomplete Dataset

UCI Dataset ( X )	Number  of  Objects with Missed Data ( nio )	Number of Objects without missed data ( NCO )
Mamographics_ Masses	131	830
Deematology	08	358
Heart_dises1	06	297
Heart_dises2	293	01
Heart_dises3	122	01
Horse_Colic	294	06

Table 3. Result of Object Consistency and Object Inconsistent Measures on the UCI Incomplete Dataset

UCI Datasets ( X )	Dataset Size ( n )	Dataset Inconsistent Level OIM ( X ) in %	Dataset Consistent Level OCM ( X ) in %
Mamographics_Masses	961	13.63	86.36
Deematology	366	2.187	97.81
Heart_dises1	304	1.9801	98.01
Heart_dises2	294	99.659	0.340
Heart_dises3	123	99.186	0.82
Horse_Colic	306	98.0	2.0

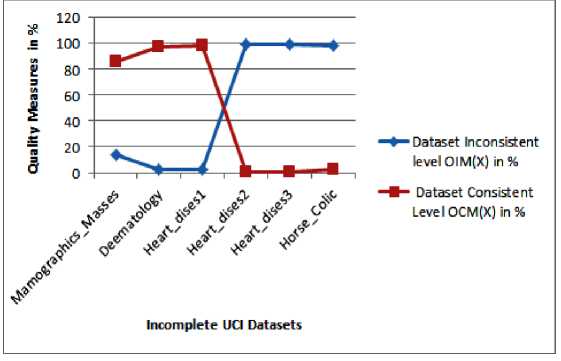
Fig.2. Result of Consistency and Inconsistency Measures on Incomplete UCI Dataset

Deematology: The proposed DDC scheme was tested on this dataset with 366 objects. First, it identified the 358 normal objects with zero degree of missing data, 08 normal objects with lesser degree of missing attributes and 0 outliers based on the INO method. The results are incorporated in Table 4. Then, the RNO method reconstructed the missed attributes in the 8 normal objects based on flanking objects and the improved dataset is presented in Table 5.

Heart_dises1: The INO identifies 297 normal objects without missing data, 06 normal objects with lesser degree of missing attributes values and 0 outliers over the dataset and the results are given in Table 4. The process of RNO reconstructed the missing attributes in 6 normal objects through its closest objects and correspondingly this modified dataset is presented in Table 5.

Heart_dises2: In this dataset, the INO method identified 01 normal object with zero degree missing data, 271 normal objects with lesser degree of missing attributes and 22 abnormal objects respectively. The result of this dataset indicated in Table 4. Next, the RNO scheme restored the missing attributes values over 271 normal objects by its closest object and the improved dataset with 272 normal objects is incorporated in Table 5.

Heart_dises3: The INO identifies 01 normal object with zero degree missing data, 116 normal objects with lesser degree of missing attributes and 06 outliers over this dataset with the results being presented in Table 4. Similarly, the RNO method recreated the missed attributes values in 116 normal objects through its closest objects and this modified dataset with 117 objects is presented in Table 5.

Horse_Colic: This dataset contains 306 objects with six attributes. The INO method identifies 06 complete objects with zero degree missing data, 125 normal objects with lesser degree of missing attributes and 175 irregular objects with a higher degree of missing attributes values. These measurements are presented in Table 4. Similarly, the RNO method is reconstructed 125 normal objects with missed attributes by its closest objects and the result is presented in Table 5.

Table 4. Result of DDC Approach Tested on UCI Incomplete Dataset

UCI Datasets ( X )	Normal Objects ( C 1 )		Abnormal Objects ( C 2 )
	Number of Objects Without Missed Data ( m - k )	Number of Objects with Lesser Degree Missed Data ( k )	Number of Objects with Higher Degree Missed Data ( n - m )
Mamographics_Masses	830	101	30
Deematology	358	08	00
Heart_dises1	297	06	00
Heart_dises2	01	271	22
Heart_dises3	01	116	06
Horse_Colic	06	125	175

Table 5. Result of Object Consistency and Object Inconsistency Measures Obtained DQM Scheme on Improved Dataset with Outlier

UCI Dataset ( X )	After the Reconstruction Process
	Number of Complete Objects ( m )	Number of Incomplete Objects ( n - m )	Dataset Consistency Level OCM ( X ) in %	Dataset Inconsistency Level OIM ( X ) in %
Mamographics_Masses	931	30	96.87	3.121
Deematology	366	00	100	0.0
Heart_dises1	303	00	100	0.0
Heart_dises2	272	22	92.51	7.48
Heart_dises3	117	06	95.121	4.87
Horse_Colic	125	175	41.66	58.33

Table 6. Result of Object Consistency and Object Inconsistency Measures Obtained with DQM Scheme on Improved Dataset without Outlier

UCI Dataset	Incomplete Dataset Size ( n )	Improved Dataset Without Outliers
		Dataset Size ( m )	Dataset Consistency OCM ( X ) in %	Dataset Inconsistency OIM ( X ) in %
Mamographics_Masses	961	931	100	0.0
Deematology	366	366	100	0.0
Heart_dises1	303	303	100	0.0
Heart_dises2	294	272	100	0.0
Heart_dises3	123	117	100	0.0
Horse_Colic	306	125	100	0.0

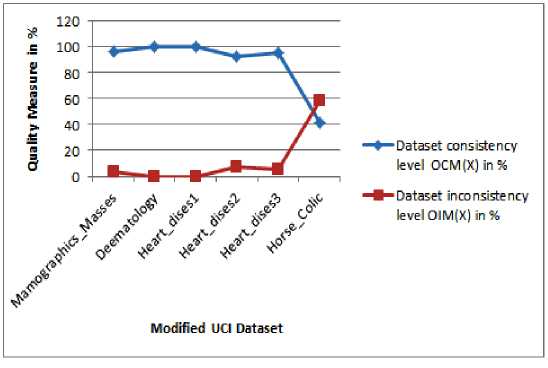
Fig.3. Results of Consistency and Inconsistency Measures on Improved UCI Dataset with Outliers

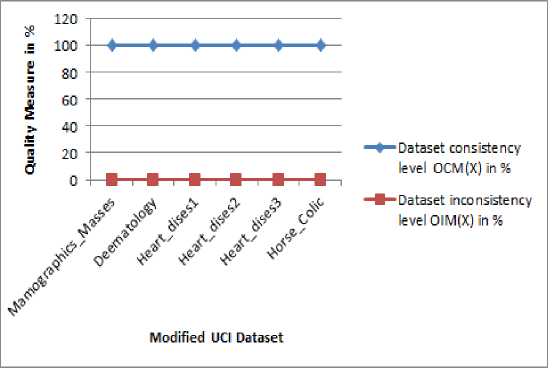
Fig.4. Results of Consistency and Inconsistency Measures on UCI Improved Dataset without Outliers

Finally, the Data Quality Measure (DQM) estimates the consistency and inconsistency of objects in % over the improved UCI datasets with and without abnormal objects as presented in Table 4. First, the DQM is calculated the consistency and inconsistency among the objects in improved UCI datasets with abnormal data in % and obtained as 96.87, 100, 100, 92.51, 95.121, 41.66 and 3.12, 0.0, 0.0 7.48, 4.87, 58.33 respectively. The results are incorporated in Table 5. Similarly, the same measures were carried out on improved UCI datasets without outliers as presented in Table 4 and the estimated results are given as 100, 100, 100, 100, 100, 100 and 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 respectively. The quality measured results are incorporated in Table 6. Fig. 3 shows the consistency measures on improved UCI datasets with outliers and similarly the Fig. 4 is illustrated the inconsistency measure of improved UCI datasets without abnormal objects. Experimental results show that the proposed DDC approach is simple and effective for improving incomplete dataset consistency from lower level to higher level through identifying normal objects and abnormal objects (outliers) over the incomplete dataset based on the degree of missing attributes without user input. All these techniques are experimented on the Dell/ T4500 machine with 2 GB RAM running windows7.

• VII.    Conclusion

In this paper, a new approach called Dynamic Data Cleaning (DDC) is presented. This approach aims to reduce inconsistency and improve dataset consistency by identifying, reconstructing and removing the incomplete data objects with missed data. The proposed (DDC) approach consists of three methods: Identify Normal Object (INO), Reconstruct Normal Object (RNO) and Dataset Quality Measure (DQM). The INO method divides the dataset into normal objects and abnormal objects (outliers) based on the degree of missing attributes data over each individual object. Similarly, the RNO method reconstructs the missed attributes values in the normal object by its closest object based on the distance metric. Finally, the DQM method intends to measure the consistency and inconsistency of the objects in the improved dataset with and without outliers. For the experimental purpose, the proposed DDC approach is tested on six bench mark UCI incomplete datasets with a lower consistency. It is found that the proposed DDC approach perfectly identified the normal objects and irregular objects (outliers) over the UCI incomplete datasets based on the IRO method. Then, subsequently, it improves the normal objects consistency from lower to higher levels by reconstructing missed attributes data in the normal objects and removing the abnormal objects based on RNO method. Experimental results show that the proposed DDC scheme is better suitable to improve the incomplete dataset consistency from a lower to higher level by reconstructing the missed data in normal data objects in the incomplete dataset without user involvement. Future work can be extended the DDC approach with a slight modification to process the incomplete big dataset.

• [1]    Mohammed A. AlGhamdi, “Pre-Processing Methods of Data Mining,” IEEE/ACM 7th International Conference on Utility and Cloud Computing, pp. 452-456, 2014.

• [2]    I. Ahmed and A. Aziz, “Dynamic approach for data scrubbing process,” International Journal on Computer Science and Engineering, ISSN: 0975-3397, 2010.

• [3]    B. Everett, Cluster Analysis, John Wiley and Sons, Inc., 1993.

• [4]    W. Kim, B.J. Choi, E.K. Hong, S.K. Kim, and D. Lee, “A taxonomy of dirty data”, Data mining and knowledge discovery, vol. 7, no. 1, 2003, pp. 81–99.

• [5]    Edwin-de-Jonge and Mark-van-der-loo, “An introduction to data cleaning with R,” Statistics Netherland, 2013.

• [6]    R. J. A. Little, “Missing-data adjustments in large surveys,” Journal of Business and Economic Statistics, vol.

• 6,    no. 3, pp. 287-296, 1988.

• [22]    http://www.ics.uci/mamographicsmasses     /     ML

Repository .html