A New EEG Acquisition Protocol for Biometric Identification Using Eye Blinking Signals

Since, today, it becomes very important to verify the identity of an individual in many applications. Traditional biometric traits currently include the finger-print, voice, face. The limitations using these traits is that they are not confidential and neither secret to an individual (less secure). For example, the finger-print is one of the most popular biometrics that is easy to collect and applicable to real time applications. However, it is vulnerable to injuries while it can also be easily falsified using artificial fingers made of silicone gel known as “ gummy fingers ” [1]. Furthermore, people leave their physical prints of finger on everything they touch. Faces are visible and can be captured at a distance, so, they can be easily disguised or forged [2]. Furthermore, face image is a two dimensional signal which requires high computational costs. Also, voices are being recorded and can be imitated easily.

To solve these problems, the research in the field of biometrics is directed to investigate the potential of bioelectrical signals as new biometric traits for human authentication. The most prominent bio-electrical signal for biometric applications is the Electro-Encephalo-Gram (EEG). EEG has some advantages, which are not shared by the traditional biometrics. One of these advantages is that EEG signals show more security since they are not exposed and therefore cannot be captured at a distance.

Also, they are less likely to be artificially generated and fed to a sensor to spoof it. In the next paragraph, a brief description of EEG signal is provided.

EEG is the electrical recording of brain activity, represented as voltage fluctuations resulting from ionic current flows within the neurons of the brain [3]. EEG can be recorded by electrodes placed on the scalp over the brain (non-invasive). The amplitude of the EEG signals ranges between 10 - 200 (Л V with a frequency falling in the range 0.5 - 40Hz. EEG waveform is classified into five different frequency bands (alpha, beta, theta, delta, and gamma bands) [4]. Delta ( 6 ) waves (0.5 -4Hz) are the slowest EEG waves, normally detected during the deep and unconscious sleep. Theta ( 6 ) waves (4 - 8Hz) are observed during some states of sleep and quiet focus. Alpha ( a ) band (8 - 14Hz) originates during periods of relaxation with eyes closed but still awake. Beta ( P ) band (14 - 30Hz) originates during normal consciousness and active concentration. Finally, Gamma ( Y ) waves (over 30Hz) are known to have stronger electrical signals in response to visual stimulation. Fig. 1 shows the five frequency bands of EEG signal. Different acquisition protocols have been tested for human recognition tasks such as relaxation with eye closed, EEG recordings based on visual stimuli, and performing mental tasks. In this paper, a new EEG acquisition protocol based on eye blinking is adopted for human recognition tasks. In the next paragraph, the origin of eye blinking signal is briefly explained.

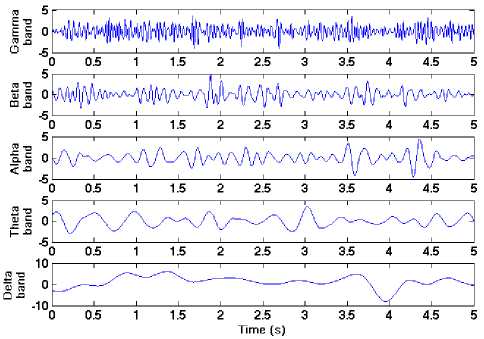
Fig. 1. The five frequency bands of EEG signal

The eyeball acts as a dipole with a positive pole oriented anteriorly (cornea) and a negative pole oriented posteriorly (retina) [5]. When the eyeball rotates about its axis, it generates a large amplitude electric signal, which is detectable by any electrodes near the eye known as Electro-Oculo-Gram (EOG) [6]. As shown in Fig. 2, when the eyeball rotates upwards, the positive pole (cornea) becomes closer to Fp1 electrode and produces a positive deflection. Similarly, when the eyeball rotates downwards, the positive pole (cornea) becomes far away from Fp1 (closer to the reference electrode) producing a negative deflection. This is similar to what happens when the eye blinks. When the eyelid closes, the cornea becomes closer to Fp1 and a positive deflection is produced. But, when the eyelid opens the cornea rotate away from Fp1 and a negative deflection is produced as shown in Fig. 3. The eye blinking signal is a very low frequency signal of range 1 - 13Hz as shown in Fig. 4.

The rest of the paper is organized as follows. Section II presents a literature review of the previous proposed algorithms for biometric authentication systems based on EEG signals. Section III describes in details the proposed eye blinking identification system. The optimal system parameters are illustrated in section IV by experiments. Finally, section V summarizes the main conclusions and future directions.

• II.    Literature Review

The work done in this field can be grouped into three categories according to the type of EEG acquisition protocol used in the authentication task.

• A.    EEG Recordings While Relaxation with Eyes Closed

  The usage of EEG signals for biometric recognition was started first by Poulos et al. (1999) [7]. The a band was represented by Auto-Regressive (AR) model and classified using Linear Vector Quantization (LVQ) and achieved a correct classification between 72% and 84% over a database of 4 genuine subjects and 71 imposters. Riera et al. (2008) collected data from 51 subjects and 36

intruders [8]. Using five different types of features, an Equal Error Rate (EER) of 3.4% in verification mode and accuracy between 87.5% and 98.1% in identification mode were achieved. Campisi et al. (2011) compared AR coefficients and burg’s reflection coefficients as features for EEG signals over a database of 48 subjects [9]. The best achieved accuracy for biometric identification system was 96.08% using burg’s reflection coefficients.

• B.    EEG Recordings While Exposed to Visual Stimuli

  This type of EEG is known as Visual Evoked Potentials (VEPs). Palaniappan et al. (2007) investigated the performance of EEG VEPs over a database of 40 subjects [10]. The energy of gamma band from 61 channel electrodes was computed as features, then, classified using Elman Neural Network (ENN). The best achieved accuracy was 98.56%. S. Liu et al. (2014) compared between the two acquisition protocols; relaxation with EC and VEPs [11]. VEPs showed better performance with accuracy of 96.25% over a database of 20 subjects.

• C.    EEGRecordings While Performing Mental Tasks

  Marcel et al. (2007) investigated the use of brain activity for person authentication based on dataset of 9 subjects performing different mental tasks [12]. The mental tasks involved imagination of right and left hand movements and generation of words beginning with the same random letter. A Half Total Error Rate (HTER) of range 8.1 - 12.3% was achieved.

• III.    Proposed System

Any biometric identification system consists of four primary modules; data acquisition, pre-processing, feature extraction and classifier module. The implemented algorithms for these modules are described in this section.

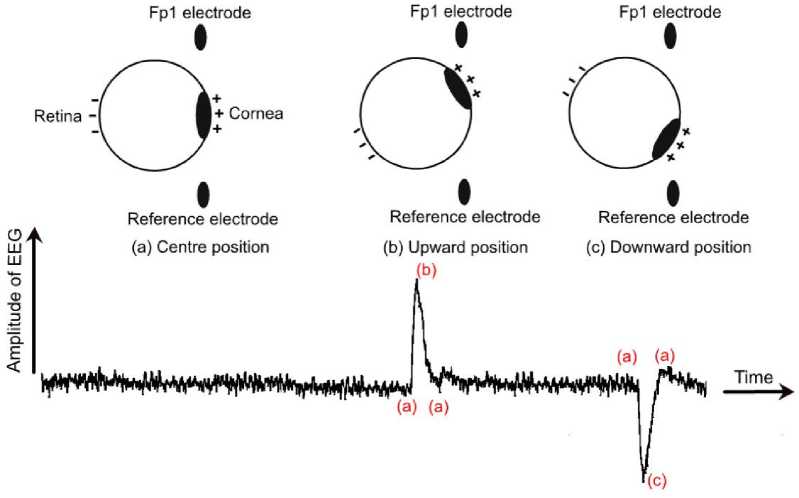
Fig. 2. The dipole model of eyeball with waveform of EEG signal when the cornea in the center (a), rotating upwards (b), and downwards (c)

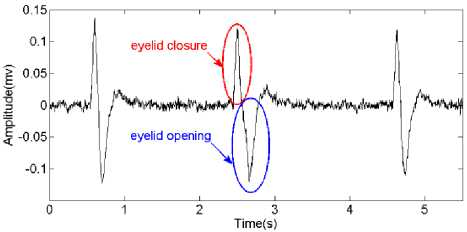
Fig. 3. The EEG signal with the waveform of eye blinking recorded using Neurosky Mindwave headset

instant of the positive peak to detect the onset of the eye blink and twice the interval dpn was added to the instant of the negative peak to detect the offset of the eye blink. This is illustrated in Fig. 6.

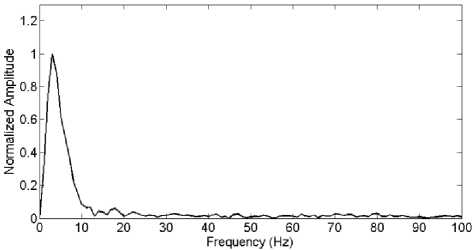
Fig. 4. The frequency response of eye blinking signal

• C. Feature Extraction Stage

In this paper, the features were extracted from the eye blinking using parametric modeling. Parametric modeling is a technique to represent the signal with a mathematical model of certain parameters [13]. The auto-regressive model is adopted in this paper. The AR model is a rational transfer function with all the parameters lies in the denominator (all-pole model). Assume we have a time sequence of length, N, s(1), s(2), ..., s(N), the current sample s(n) can be predicted as a linear weighted sum of the previous p samples where p is the order of the AR model. This can be expressed as follows

S (n) = -£a(i)s(n-i)

where the weight, a(i), represents the I^th coefficient of the AR model. The error between the predicted value, S (n), and the actual value, s (n) , is called the forward prediction error, e (n) , which is given by

• A.    Data Acquisition

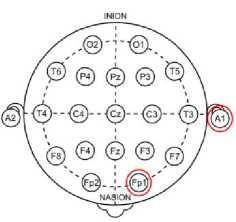
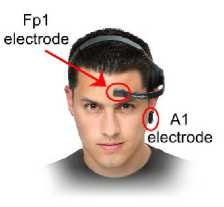
All EEG signals used in this paper were recorded using Neurosky Mindwave headset. The headset consists of an ear-clip and a sensor arm as shown in Fig. 5. The reference and ground electrodes are on the ear clip (A1 position) and the EEG electrode is on the sensor arm, resting on the forehead above the eye (Fp1 position). The sensor is made of dry electrode which does not require any skin preparation or conductive pastes. The sampling rate of the device is 512Hz. The raw EEG signal was collected from 10 subjects with age ranging between 21 -31 years in a quite environment. In one session, 6 - 8 trials of EEG signal was recorded of 20 seconds each. The volunteer was asked to make 8 - 12 eye blinks in each trial. The EEG signals of 6 subjects were recorded in two sessions with a separation of more than two weeks while the rest was in one session. MATLAB software was used for recording the EEG data from Neurosky headset and further processing.

• B.    Pre-processing Stage

The eye blinks were extracted form EEG using the following criterion. Eye blinking has the largest amplitude in EEG signal so it can be easily detected from its peaks. First of all, the EEG signal was normalized to have zero mean and maximum amplitude of one. Then, a certain threshold was adopted to detect the positive and negative peaks of the eye blink. By examining all the acquired EEG data, it was found that the positive peak of eye blink is always greater than 0.3 and the negative one is smaller than -0.3 (after normalization). The MATLAB function used for peak detection was “findpeaks” with a minimum peak height of value 0.3. Then the duration between the positive and negative peaks, d_pn , was calculated. Then, the interval d_pn was subtracted from the

e (n) = s(n) - S(n) p = s(n) + ^ a(i)s(n - i) 1=1

then, the mean squared error, E, is calculated as

_£=lV_e 2 (n)              (3)

N 4—к n=1

(a)

Fig. 5. The international 10-20 system for EEG electrodes with the electrodes of the Neurosky headset highlighted in red circles

(b)

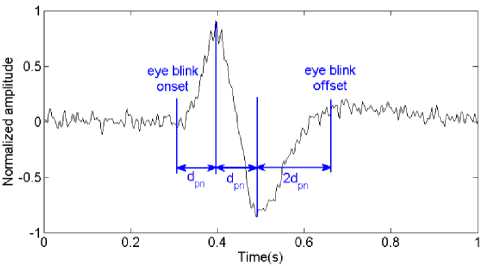
Fig. 6. Proposed algorithm for eye blinking extraction

1 N /          Р                 х ²

E = N У ( s ⁽ⁿ⁾ + У ^a(0s⁽ ™ - О )

п=1V        / = 1              /

The best fit of the AR model is to choose

the

coefficients, a(i), that minimizes E .This is called squares error algorithm which can be achieved by dE

—— = 0,for i = 1,2,^, p da (i)

this yields the following matrix

least-

[

r(0)

r ⁽ 1)

r ⁽ 1)

r(0)

... r(p)

... r(p - 1)

. ( (р - 1)

r(p - 2)

-

...     r(0)

"r (1)"

r (2)

a(1)l a(2) a(p)J

r (p )

where r(Z) is the auto-correlation function of the time sequence ( ) for the time shift, , which is given by

N

((Г) = 1У s(n)s(n - I) IN 4—к

n=l

The set of equations in Eq. (6) is known as YuleWalker which describes the unknown AR coefficients in terms of p + 1 autocorrelation coefficients. These equations can be solved recursively using Levinson-Durbin algorithm or Burg algorithm [13]. The difference between the two algorithms is that the former minimizes the forward prediction error while the later minimizes the forward and backward prediction errors. In backward prediction, the value of sample (  -  ) is predicted as a weighted sum of the future samples as following

p

s (n - p) = - У a(i)s(n - p + I)

i=l and the backward prediction error is

b (n) = s(n - p) - S(n - p)

p

= s(n - p) + У ct(i)s(n - p + I)

i=l

In this paper, a comparison between Levinson-Durbin and Burg algorithms is tested on the performance of our biometric identification system. The Levinson-Durbin algorithm is implemented in MATLAB using the function “aryule” , while the Burg algorithm is implemented using the function “arburg” .

D. Classification Stage

In this paper, the Discriminant Analysis (DA) is adopted for the classifier stage of the proposed system. DA assumes that the features extracted from every class, c , have a multivariate Gaussian distribution as follows [14]

P c (%) =----¹---__е4(х-мс)^_с-Ч^а

(2я) 2 |£ с | 2

where p is the dimension of the feature vector x which is the order of the AR model as mentioned earlier. p_c and E_c are the mean and the covariance of the feature vectors of class c. The classifier decision is performed using the optimum Bayes rule which maximizes the posterior probability or its logarithm as shown in the following equation

G(x) = argmax [-1log|Ej c      2

-

- ⁽x-p_с)^т Е_с (Хх — c c )     ⁽¹¹⁾

+ iog(/ C )]

where is the prior probability of class which is assumed to be uniform (f_c = 1/c) and G(x) is the probability that the unknown feature vector, x, belongs to class c. Eq. (11) represents a Quadratic Discriminant Analysis (QDA) problem where the boundaries between the different classes are determined by a quadratic function. This is illustrated in Fig. 7. A simpler classifier assumes that all the classes have the same covariance, i.e., E_c = E for all values of c. Now the first term in Eq. (11) will be constant and can be discarded to obtain the following equation

G to = arg max [- ^{1 (} x - c ^)T E ^{1 (} x-p c ) ²       i                      (12)

+ logG C )]

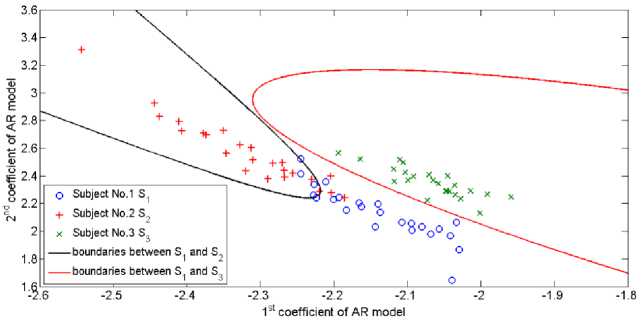
Fig. 7. Demonstration of QDA classification where the boundaries set between the three classes are represented by a quadratic function

This is a Linear Discriminant Analysis (LDA) problem where the boundaries between the different classes are determined by a straight line. This is illustrated in Fig. 8. In this paper the MATLAB function “classify” is used to implement QDA and LDA classifiers.

• IV.    Experimental Setup and Results

The experimental setup of the proposed identification system is divided into two phases; the training phase and testing phase. Every time the experiment is run, 62 eye blinking samples are selected randomly for each subject from the whole set of trials. Then, features are extracted to generate 62 feature vectors. After that, 38 samples out of 62 feature vectors are selected randomly for the training phase and the remaining 24 vectors are averaged to generate the test sample. The performance of the system is evaluated using the Correct Recognition Rate ( CRR_av ). CRR_av is the average number of times (probability) the system correctly identifies the subjects over a certain number of trials J which can be calculated as follows

CRR ( )

Number of correctly identified subjects b

Total number of subjects

J

CRR_av = ¹ ∑ CRR ( )

J i=i

The experiment is run for about 200 times ( J = 200), then, the average, minimum, and maximum CRR are obtained.

The proposed identification system using eye blinking signal is tested under different parameters. Namely, these parameters are; the order of the AR model and the number of testing samples. These parameters are tested using the two algorithms for AR modeling previously mentioned; Levinson-Durbin and Burg algorithms. Also, the performance of the system is evaluated using LDA and QDA classifiers. Fig. 9 shows the performance of the proposed system under different orders of AR model with the average, minimum, and maximum CRR . As shown, the CRRav increases as the order of AR model, p, increases until p=10 and then the CRRav remains approximately constant. We conclude that AR model of order 10 is sufficient for representation of eye blinking signal to obtain high CRRav . The best CRRav obtained in this test is 99.8% approximately. This test is performed using LDA classifiers and Burg algorithm for AR modeling and 24 testing samples.

The performance of the proposed system under different number of test samples is evaluated in Fig. 10. The CRRav increases as the number of test samples increases and becomes approximately constant when more than 15 testing samples are used. So for testing phase, only 15 samples, i.e. 15 eye blinking signals, are required. This test is performed using LDA classifiers and Burg algorithm for AR modeling and a model of order 20.

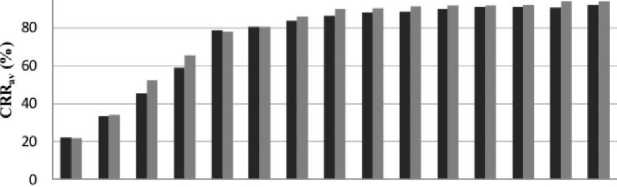
Fig. 11 shows a comparison between the system’s performance using LDA and QDA classifiers for different values of model order. From the achieved results, LDA shows a better performance than QDA classifier. This test is performed using Burg algorithm for AR modeling and a model of order 20 using 24 test samples. Fig. 12 shows a comparison between the two algorithms for AR modeling. Burg algorithm shows better performance than Levinson-Durbin algorithm. This is because Burg algorithm minimizes the forward and backward prediction errors while the Levinson-Durbin algorithm minimizes only the forward prediction error.

• V.    Conclusions and Future Directions

In this paper, a new acquisition protocol for EEG human recognition was proposed based on eye blinking recordings. AR modeling was adopted as a feature extraction technique for the eye blinks extracted from EEG signal. Two algorithms for AR modeling and two classification schemes were tested in this paper. Burg algorithm achieve better identification rate than Levinson-Durbin algorithm for the same order of AR model. Also, LDA performed better than QDA in the classification between subjects. Using Burg Algorithm and LDA classifier, we achieved best correct identification rate of 99.8%. This proves that eye blinking signals are unique and able to discriminate subjects.

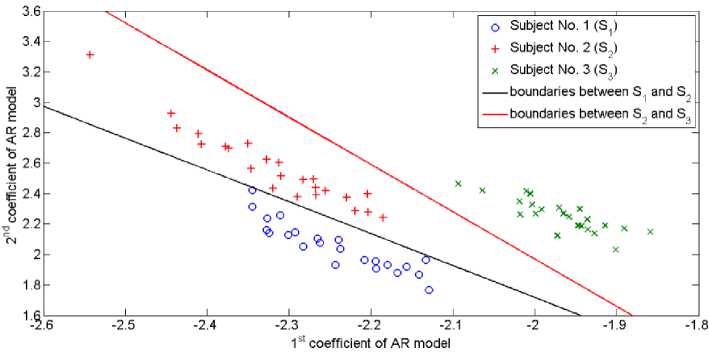
Fig. 8. Demonstration of LDA classification where the boundaries set between the three classes are represented by a straight line

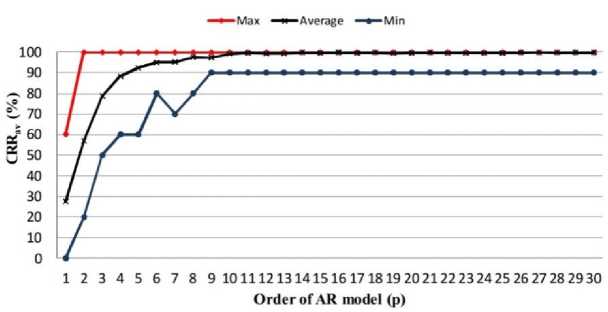
Fig. 9. Performance evaluation of the proposed system under different orders of AR model

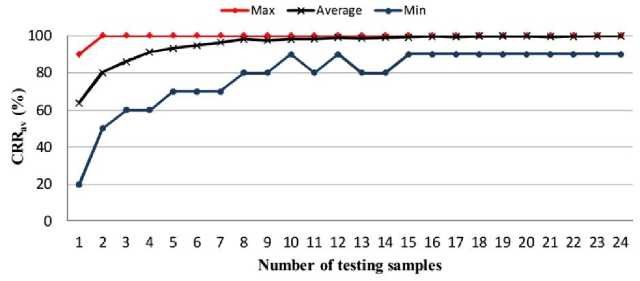
Fig. 10. Performance evaluation of the proposed system under different number of test samples

■ IDA classifier ■ QDA clasifier

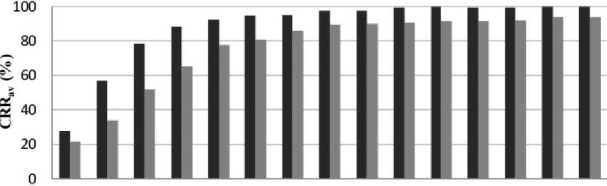
1    2    3    4    5    6    7    8    9    10 11 12 13   14 15

Order of AR model (p)

Fig. 11. A comparison between LDA and QDA classifiers for the first 15 orders of AR model

■ Levinson-Durbin algorithm ■ Burg Algorithm

1    2    3    4    5    6    7    8    9   10 11 12 13 14 15

Order of AR model (p)

Fig. 12. A comparison between Levinson-Durbin and Burg Algorithms for the first 15 orders of AR model

Although the work done in this paper shows the ability to discriminate between subjects using only the eye blink signal extracted from EEG recordings, the database used has a small scale (10 subjects only). So, a larger database has to be collected and tested. Also, different feature extraction and classification techniques can be tested. Fusion at feature and decision levels can also be adopted to enhance the performance of the system [15], [16]. A comparison between the proposed approach and EEG biometric systems based on different recordings such as:

EEG during relaxation; VEPs; and imagination of performing mental tasks may be conducted to find the best approach for authentication task.

• [16] S. Prabhakar and A. K. Jain, “Decision-level fusion in fingerprint verification,” Pattern Recognition , vol. 35, no. 4, pp. 861–874.