A New Entropy Weight for Sub-Criteria in Interval Type-2 Fuzzy TOPSIS and Its Application

Published Online January 2013 in MECS

One of the well known methods in multi criteria decision making (MCDM) is Technique for Order Preference by Similarly to Ideal Solution (TOPSIS). The technique was developed by Hwang and Yoon [1]. The basic concept of this method is the selected alternative should have the shortest distance from the positive-ideal solution and the farthest distance from the negative-ideal solution. There have been many research used this method in solving numerous decision making problems [2], [3], [4], [1]. However, the original fuzzy TOPSIS is not always suitable to represent uncertainties due to the usage of type-1 fuzzy set (T1FS). Therefore, type-2 fuzzy set (T2FS) was proposed by Zadeh [6] to handle uncertainty. This breakthrough came about ten years after he proposed

T1FS [7]. Unfortunately, T2FS is highly complicated computations, thereby difficult to use in real life applications. Thus, Liang and Mendel [8] developed with the new concepts of T2FS that make computations more manageable. In the new concepts, there are upper membership function and lower membership function that represented by T1FS membership function. The area between these two functions is footprint of uncertainty (FOU), which is used to characterize T2FS. Although T2FS have been widely applied in many areas, most researchers used interval T2FS (IT2FS) in practical fields because of the computational complexity involved in using T2FS [9]. Zhang [9] introduced interval type-2 rough fuzzy set as a combination of IT2FS and rough set theory. He also manage to get the relationship between IT2FS and interval type 2 fuzzy topology operators. Chen and Lee [10] have developed fuzzy TOPSIS based on IT2FS to choose the best candidate from a set of alternatives. They extended the TOPSIS method from Hwang and Yoon [1] using IT2FS instead of T1FS.

One of the important steps in fuzzy TOPSIS is defining weights. In fuzzy TOPSIS, weights can be divided into two types which are subjective weight and objective weight. Subjective weight can be obtained based on information of the attributes from the decision makers through questionnaires, interviews or trade-off interrogation directly [11]. This subjective weight can reflect the strength of decision makers’ judgment. On the other hand, objective weight can be obtained from the objective information such as decision matrix through mathematics models [1]. Wang and Lee [12] proposed these both weights into fuzzy TOPSIS. In their paper, the subjective weights that given by decision makers need to be normalized into comparable scale and adopted end-user rating as the objective weight based on Shannon’s entropy theory. Zamri and Abdullah [13] proposed a new weight based on Fuzzy Rasch Model and IT2FS. With this merger, they applied it into interval type-2 fuzzy TOPSIS. Then, a case study on road accident in Malaysia was performed to demonstrate the feasibility of the new method.

TOPSIS has become a favorable technique in solving MCDM problems because the concept is reasonable, easy to understand and it needs less computational effort. With these low computational risks, we propose some modifications on the interval type-2 fuzzy TOPSIS. In this paper, four level hierarchy problems are proposed instead of three level hierarchy problems. The first modification is made to obtain more details about goal, criteria, sub-criteria and alternatives. Many researchers have given little attentions on the four level hierarchies as they argued that the criteria and subcriteria are already included in decision factors. However, Shahanagi and Yazdian [14] insisted that these criteria and sub-criteria are indeed meaningful and the most important measures in MCDM. The criteria and sub-criteria have been indicated in many application papers such as in vendor selection [15], and supplier selection [16],[17]. Moreover, the existing method that used subjective weight has a weakness. The fuzziness and the vagueness of human judgment and preference make it difficult to be applied in practice [18]. Therefore, this paper proposes second modification by introducing objective weight in interval type-2 fuzzy TOPSIS. Specifically entropy weight is proposed to use as the method of finding weight for sub-criteria in interval type-2 fuzzy TOPSIS. The idea of entropy method that used by Cui [18] is employed in this proposed method.

The entropy method is basically used in rating the criteria but in this paper we apply the method in rating the sub-criteria. Besides, there have been cases where value of entropy is in crisp [19] ,[20]. As to overcome the limitation that crisp value unable to handle fuzziness and vagueness, we propose an equation that gives result in linguistic value. This paper aims to overcome the issues of sub-criteria and objective weight in interval type-2 fuzzy TOPSIS. Specifically, the objective of this paper is to propose a new entropy weight for sub-criteria in interval type-2 fuzzy TOPSIS. A case of supplier selection is chosen to illustrate of the proposed method. Decision making in supplier selection is important as inappropriate decision of supplier will affect the entire supply chain of the firm [21].

The rest of this paper is organized as follows. Section II briefly reviews the concept of IT2FS and entropy method. Section III presents the proposed new entropy in interval type-2 fuzzy TOPSIS. An example of the implementation of the proposed method for a case of supplier selection is described in Section IV. Finally, this paper is concluded in Section V.

• II.    Basic definitions and notation

• 2.1    Entropy weight.

The entropy is used to calculate the weight of subcriteria. Below are some reviews of the entropy:

• i.    Shannon and Weaver [22] employed the entropy to estimate uncertainty of object based on information theory using probability function. It can be represented by

q

H ⁽ P ⁽ x )) = - k ^ P ⁽ x ^{) ln} P ⁽ x )

k = 1                                        (1)

where, H is the level of entropy. It represents the p probability of j occurrence of event.

• ii.    The greater the value of the entropy, the smaller the entropy weight, then the smaller the different alternatives in this specific attribute, and the less information the specific attribute provides, and the less important this attribute becomes in decision making process. The entropy value can be calculated using the formula,

n ej = -k ^ Pj In Pj j=1

where ^k is a constant, let

k = —.

ln m

• iii.    De Luca and Termini [23] define non-probabilistic entropy of fuzzy set. It is a measure the degree of fuzziness of fuzzy set A ⁽ x ) . This definition uses the

,     , ■       „               u ~ ( x )

membership function ^A     to replace the

Shannon’s probability function ^{P (} x ^k ) by

H ⁽ ~ ^{( x} ) ) = - ^k ^ UA ⁽ x k ^{) ln} UA ⁽ x k )

^k = 1                                      (3)

where k is the normalized constant which equals to 1 lnq iv.

Szmidt and Kacprzyk [24] developed entropy method for intuitionistic fuzzy set (ITS). They proposed IF entropy as a ratio distances between the ⁽ F , F ear ) and , far^ as stated below:

E sk ( F ) =

, near

( F , F far )

• 2.2    Type -2 Fuzzy set [25].

~

Definition: A type-2 fuzzy set ^A in the universe of discourse X can be represented by a type-2

Ц ~ membership function A shown as follows

X = J J Ц х ( x ’ u )/( x ’ u )’ x е D ~ u е J_x c [ 0,1 ]

= J J   V (x, u )> xеD~ uе Jx c[0,1]

А =

^V х

< (( x u ) Ц ⁽ x u^

<

е X

^G J x ^ ^[Ь Ц ^{( х} u ) <

x ^е d x

J /(u) Iх

. и е J, ₌[ ]  J/

where, ^x called the primary variable , has domain

where, J x denotes an interval in ^[ 0^{,1 ]} . Besides, the

~ type-2 fuzzy set A also can be represented as follows:

D ~ ;u е [ 0,1 ]

called the secondary variable , has

J c[0,1]         x е D ~; Jr domain x , at each      X x

is also called the

~

A =

~

J  j ц ~ ( x , u )/( x , u )

support of the secondary MF, and the amplitude of

^{Ц х (} x ’ u ) , called a secondary grade of X , equals 1 for

x е X u е J_x

^V x ^е D X and ^{V u е J}x ⁽ [0- ^{l ]}

J      JJ where, x and      denotes the union over all admissible x andu .

~

Definition: An IT2FS ^X is characterized by its membership function (MF) ^{Ц х (} x ’ u ) , i.e.,

• 2.3    Trapezoidal membership function [26]

Definition: [26] The upper membership function and the lower membership function of an interval type-2 fuzzy set are type-1 membership functions, respectively.

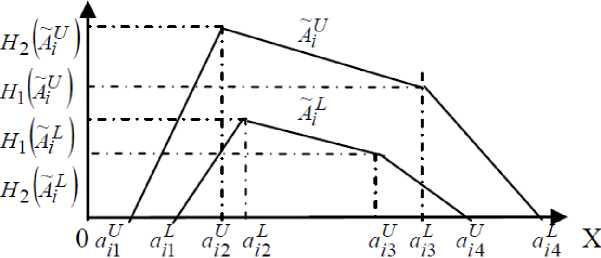
Fig. 1: The upper trapezoidal membership function

A~U i and the lower membership function

~

AL i of the interval type-2 fuzzy set

~

_~ A _i

III. The Proposed method

Step 1: Construct the decision-maker and create matrix defined as follows:

Y decision ^p of the p- t h the average decision ^Y

.~.

~

~

~

fij

where:

/ ~   ~~ \ r-~J ,        ~-- -~-- ,

~-1 ® ~ ф^ф ~

k

V7

is an interval

A ₁

Y = A 2

A m

	C 1	C 2     -		C n
S 11	S 12	S 21	S 22    '''	S ns
		z^	z^	z^
z^^	z^z	z^z	z^z	z^z
~ p f 111	~ p f 112	~ p f 121	~ p f 122	~ p f 1 ns
~	z^	z^	z^	z^
	z^	z^	z^z	z^z
~ p f 211	~ p f 212	~ p f 121	~ p f 222	~ p f 2 ns
~	z^	z^	z^	~
	z^	z^	z^z
~ p f m 11	~ p f m 12	~ p f m 21	~ p f m 22	~ p mns

¹ <  j <  n 1 <  l <  s

type-2 fuzzy set, ¹ <  i <  m , 1 <  p <  k and s denotes the

number of sub-criteria and k denotes the number of

decision makers.

~ ^u

Step 2: Calculate ^jl the weight of the decision maker, k with respect to the sub-criteria.

As mentioned before, we apply entropy method to avert subjectivity of human preference. This method is developed by Cui [18].

Construct entropy value for sub-criteria as follows:

—

^ejl =

fijl log fijl i=1_________________ logm

where M P ^{( A /)} = a P ⁺ a i l p +1 ) )/ ² ,1 <  P <  ³

q +

Sq(~j)=. 7X

a

—

1 q ⁺¹

² k = q

,

Calculate the weight of sub-criteria formula as follows:

_u ~ _jl

using

aiqj standard deviation for and

a jq + 1 ) 1 <  P <  3

,

.

~ ujl =

1  ~

^1—~ jl

ms j =1 l =1

For example,

Step 3: Calculate the weight of criteria

w_j

S4(~ )= 1X -

У k=q I

aikj

₁4 _j

4 X a ik k = q

2 is

ms

~ = XX S ji j = 1 1 = 1

ajajajaj standard deviations for   i1 , i2 , i3 , i4

.

denotes the membership value of the element

^hp ⁽ A i ) a ijP + 1 ) _in

Y

Step 4: Construct the weighted decision matrix ^w :

Since we used four level of hierarchy, there will be multiplication operation on the three fuzzy numbers wj which are weight of criteria, , weight of sub-criteria,

_A ~ _j the trapezoidal membership function ⁱ j e { U , L }

1 <  p <  3

,

,

.

Step 6: Determine the positive ideal solution negative ideal solution x ^- where:

x

⁺ and

~

u jl and fuzzy rating of each alternative,

~ ^f ijl

.

+    ( +   +        + xjl =(v11, v12,-, vns

У, =(~ )

w ij m )т г x n

A ₁

= A 2

A m

~ where, vijk

1 <  l <  s

.

~

S ₁₁ v ^~ _{111 ~} v 211

~ vm11

C 1

S ₂₁

~ v112

~ v212

~ vm12

~~

-

■s ns

_~

— ‘

_~

— ‘

~ vmns

w j ® ~ ji ® j 1 <  i <  m 1 <  j <  n

,

and

Step 5: Calculate the ranking values Rank (v ij ) of the interval type-2 fuzzy set (v ij ) , using the equation

Y W = ( ^{Rank I v}  ^ _x n

Where

1 <  i <  m ¹ <  ^j <  n , ,

Rank ^ A i j = M 1 ( A U ) + M 1 ( AL ) + M 2 ( A U ) + M 2 ( A L ) + M 3 ( A U ) + M 3 ( A L ) — 1 ( S 1 ( A U ) + S 1 ( A L ) + S 2 ( a U ) +

S 2 ( A L ) + S 3 ( ~ U ) + S 3 ( ~ L ) + S 4 ( A U ) + S 4 ( ~ L )) + H 1 ( ~ U ) + H 1 ( A L ) + H 2 ( A U ) + H 2 ( a l )

xjl =^{( v} 11^{, v} '2,-

, v_ns

| max { Rank ( v jl )} ^f min { Rank ⁽ ~ l ^{)} fi}

^e F i

^e F 2

min {Rank ( v j )} f i ^e F

)     |1s j <

max

1< j <  n

^Rankvjl )} f i - ^e F 2

Step 7: Calculate the distance between

each

alternative for the positive and negative ideal solution as shown as follows, where¹ <  ^j <  ⁿ ,1 <  ^l <  ^s :

n

d ⁺⁽ x^l ) = i X ( Rank ^{( v} j ^)— v + i ) .

n

d ⁽ x i ) = i X (Rankv j ^)— v j¹ ) .

j =1 (19)

Step 8: Calculate the relative degree of closeness between each alternative A i and the positive ideal solution x⁺ and negative ideal solution x^- we denote it by C(A i ) .

c ( a ) =— .^d / Ai )_z . ^{k ;}  d ⁺ ( a ) + d ^— ( a )

Step 9: Sort the values of C(A i ) in descending sequence. The larger value of C(A_i) , the higher preference of the alternatives A_i .

• IV.    Numerical Example

In this study, the numerical example from Shahanagi & Yazdian [14] is retrieved to illustrate the proposed method. Assume that a company intends to make decision on supplier selection. Three criteria, subcriteria and alternatives are identified. The hierarchical structure of the decision problem is shown in Figure II.

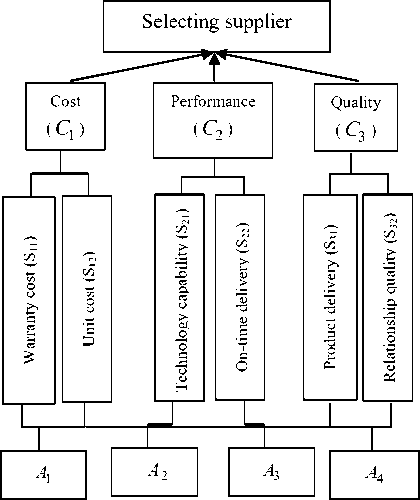
Fig. 2: The hierarchical structure of the decision problem

These linguistic variables that retrieved from [14] are trapezoidal fuzzy number. In this numerical example, the linguistic variables are presented as interval type-2 fuzzy set.

The three decision makers use the linguistic terms defined in Table I.

Implementation of the proposed method is presented in the step-wise as follows.

Step 1: Decision matrices Y ¹ , Y ² and Y ³ of the alternatives A ¹ , A ² , A ³ and A ⁴ are constructed respectively given in Table II, Table III and Table IV:

Table 2: Evaluating values of alternatives of the decision maker 1 with respect to different attributes

Criteria	C1		C2		C3
Sub-criteria	S11	S12	S21	S22	S31	S32
A1	G	VG	G	MG	G	G
A2	MG	G	VG	G	G	MG
A3	F	G	G	VG	VG	F
A4	F	F	VG	MG	MG	MG

Table 3: Evaluating values of alternatives of the decision maker 2 with respect to different attributes

Criteria	C1		C2		C3
Sub-criteria	S11	S12	S21	S22	S31	S32
A1	VG	VG	F	MG	MG	MG
A2	G	G	G	G	G	F
A3	MG	G	MG	VG	G	MP
A4	F	MG	G	MG	G	MG

Table 4: Evaluating values of alternatives of the decision maker 3 with respect to different attributes

Criteria	C1		C2		C3
Sub-criteria	S11	S12	S21	S22	S31	S32
A1	G	VG	G	G	G	VG
A2	VG	G	G	VG	G	MG
A3	G	VG	MG	VG	VG	MP
A4	MG	G	G	F	G	MG

Based on (9), the average decision matrix is constructed as follows:

Table 1: Linguistic terms and their corresponding interval type-2 fuzzy set

Linguistic Terms	Interval Type-2 Fuzzy Sets
Very Poor (VP)	((0,0,0.1,0.2;1,1), (0,0,0.1,0.2;1,1))
Poor (P)	((0.1,0.2,0.2,0.3;1,1), (0.1,0.2,0.2,0.3;1,1))
Medium Poor (MP)	((0.2,0.3,0.4,0.5;1,1), (0.2,0.3,0.4,0.5;1,1))
Fair (F)	((0.4,0.5,0.5,0.6;1,1), (0.4,0.5,0.5,0.6;1,1))
Medium Good (MG)	((0.5,0.6,0.7,0.8;1,1), (0.5,0.6,0.7,0.8;1,1))
Good (G)	((0.7,0.8,0.8,0.9;1,1), (0.7,0.8,0.8,0.9;1,1))
Very Good (VG)	((0.8,0.9,1,1;1,1), (0.8,0.9,1,1;1,1))

		C 1		C 2	C
	S 11	S 12	S 21	S 22	S 31	S 32
Y = A 2	/ .11 ~ f 211	~ f 112 ~ f 212	~ f 121 ~ f 221	~ f 122 ~ f 222	~ f 131 ~ f 231	~ f 132 ~~ f 232
A 3	~ f 311	~ f 312	~ f 321	~ f 322	~ f 331	~ f 332 ~
A 4	L f 411	~ f 412	~ f 421	~ f 422	~ f 431	f 432 J

For example, the elements of decision matrix is given as,

~ f1П = ((0.73,0.83,0.87,0.93;1,1), (0.73,0.83,0.87,0.93;1,1))

~

У ₂₁₁ = (( 0.67,0.77,0.83,0.90;1,1), ( 0.67,0.77,0.83,0.90;1,1 ))

~

У _П1 = (( 0.53,0.63,0.67,0.77;1,1) ( 0.53,0.63,0.67,0.77;1,1 ))

~ f411 = ((0.43,0.53,0.57,0.67;1,1), (0.43,0.53,0.57,0.67;1,1))

Step (12).

3: Calculate

W =

^C ~ ¹

^{[ w} 1

the

C ₂ w ₂

weight of criteria

— w3

]

w _j

~

using

_~ ^u

Step 2: Calculate ^jl the weight of the decision maker, k with respect to the sub-criteria.

Using (10), the entropy value for sub-criteria is given as,

~    ( ( 0.35742,0.35389,0.34759,0.33935;1,1 ) , )

W1 = I /                                                          \ I

• ¹   к ( 0.35742,0.35389,0.34759,0.33935;1,1 ) J

  ~    f ( 0.3892,0.37845,0.37338,0.36247;1,1 ) , )

W2 = I                                                      I

• ²   к ( 0.3892,0.37845,0.37338,0.36247;1,1 ) J

~ 11 =

к'

~ 12 =

к'

~ e 21 =

к

( 0.8623,0.7070,0.6262,0.4568;1,1 ), ( 0.8623,0.7070,0.6262,0.4568;1,1 )

( 0.7148,0.5154,0.4132,0.2618;1,1 ) , ( 0.7148,0.5154,0.4132,0.2618;1,1 )

( 0.7579,0.5634,0.5060,0.3111;1,1 ), ( 0.7579,0.5634,0.5060,0.3111;1,1 )

W 3 =

f ( 0.253 3 8,0.26766,0.27904,0.29818;1,1 ), ^

_к( 0.25338,0.26766,0.27904,0.29818;1,1 ) ^J

Step 4: From (13), we can get the weighted decision

Y

matrix as ^w as follows.

~ e 22 =

~ e31 =

к

( 0.7816,0.6052,0.4622,0.3201;1,1 ), ( 0.7816,0.6052,0.4622,0.3201;1,1 )

( 0.7444,0.5464,0.4691,0.2710;1,1 ) , ( 0.7444,0.5464,0.4691,0.2710;1,1 )

C 1			C 2		C 3
	S 11	S 12	S 21	S 22	S 31	S 32
	г ~					~ “I
		~	~	~	~	~
Y = A1	v 111	v 112	v 121	v 122	v 131	v 132
	~	~	~	~	~	~
A 2	v 211	v 212	v 221	v 222	v 231	v 232
	~	~	~	~	~	~
A 3	v 311	v 312	v 321	v 322	v 331	v 332
		~	~	~	~	~
A 4	L v 411	v 412	v 421	v 422	v 431	v 432 _

~ e32 =

.9558,0.8656,0.7598,0.6031;1,

.9558,0.8656,0.7598,0.6031;1,

~

1) The weight for sub-criteria ^jl is calculated using (11). It is shown as,

~    f ( 0.11638,0.13334,0.13526,0.14386;1,1 ), )

uw = I                                                       I

¹¹ к ( 0.11638,0.13334,0.13526,0.14386;1,1 ) J

~   _f ( 0.1846,0.17972,0.19461,0.18005;1,1 ) , 3

u ²² =к ( 0.1846,0.17972,0.19461,0.18005;1,1 ) )

~   _f ( 0.24104,0.22055,0.21233,0.19549;1,1 ), 3

u ¹² =к ( 0.24104,0.22055,0.21233,0.19549;1,1 ) ^J

~   _f ( 0.21602,0.20647,0.19211,0.193 06;1,1), 3

u ³¹ =к ( 0.21602,0.20647,0.19211,0.193 06;1,1 ) ^J

~     f ( 0.2046,0.19874,0.17877,0.18243;1,1 ), 3

u? = 1                                                                1

²¹ к ( 0.2046,0.19874,0.17877,0.18243;1,1 ) J

~   _f ( 0.03736,0.06119,0.08693,0.10511;1,1 ), 3

u ³² =к ( 0.03736,0.06119,0.08693,0.10511;1,1 ) )

For example:

~ _ f ( 0.0305,0.0393,0.0407,0.0456;1,1 ), ^ ⁴¹¹ =к ( 0.0305,0.0393,0.0407,0.0456;1,1 )^J

~    _ f ( 0.0277,0.0362,0.0392,0.0439;1,1 ), ^

v ²¹¹ =к ( 0.0277,0.0362,0.0392,0.0439 )    J

~    _ f ( 0.0222,0.0299,0.0313,0.0374;1,1 ),³

v ³¹¹ =к ( 0.0222,0.0299,0.0313,0.0374;1,1 ) ^

~ _f ( 0.0180,0.0252,0.0266,0.0325;1,1 ),³ v ⁴¹¹ = к ( 0.0180,0.0252,0.0266,0.0325; 1,1 ) _v

Step 5: Using (15), the ranking values of the interval type-2 fuzzy set can be calculated as follows, Rank ( ~_m ) = 0.0349 + 0.0349 + 0.04 + 0.04 + 0.04315 + 0.04315 - 1 ( 0.0044 + 0.0044 + 0.0007 + 0.0007 + 0.0024 + 0.0024 + 0.0054 + 0.0054 ) + 1 + 1 + 1 + 1 = 4.2297

Thus,

Rank

Rank

Rank

Rank

Rank

Rank

Rank

Rank

Rank

Rank

Rank

Rank

( ~₂₁₁ ) = 4.2154,Rank ( ~₃₁₁ ) = 4.1755,

⁽ ~ 411 ^):

⁽ ~ 212 ^):

⁽ ~ 412 ^):

⁽ ~ 221 ^):

⁽ ~ 421 ^):

( ~ 222 )

⁽ ~ 422 )

( ^~~v231 )

( ^~~v431 )

⁽ ~ 232 )

⁽ ~ 432 )

= 4.1480,Rankl

= 4.3608,Rankl

= 4.2918,Rankl

( ~ 112 ) : ( ~ 312 ) ^{; (}~ 121^):

= 4.4189,

= 4.3813,

= 4.2938,

= 4.3569,Rankl

= 4.3569,Rank

= 4.3478,Rankl

■ ⁽~ 321 ^):

■ ⁽~ 122 ^):

^:(~ 322 )

= 4.3153,

= 4.2861,

= 4.3820,

= 4.2440,Rank ( ~₁₃₁ ) = 4.2413,

= 4.2579,Rankl

= 4.2413,Rankl

= 4.0686,Rank

= 4.0745

⁽ ~ 331 ^{): (} ~ 132 ^):

^:(~ 332 )

= 4.2876,

= 4.0905,

= 4.0461,

Based on (14), the ranking weighted decision matrix is constructed as follows,

"4.2297 4.4189 4.2938 4.2861 4.2413 4.0905

4.2154 4.3608 4.3569 4.3478 4.2579 4.0686

Y = w 4.1755 4.3813 4.3153 4.3820 4.2876 4.0461

4.1480 4.2918 4.3569 4.2440 4.2413 4.0745

Step 9: Since C ⁽ A ¹ ) >  C ⁽ A ² ) >  C ⁽ A ³ ) >  C ⁽ A 4 ) , the preferred order of the alternatives is A ¹ >  A ² >  A ³ >  A ⁴ . Therefore, the best alternative is A ¹ .

This problem was tested by Shahanagi and Yazdian [14] and the ranking order was obtained as A ² >  A 1 >  A 3 >  A 4 . However, with the applications of interval type-2 in fuzzy TOPSIS and the new entropy for sub-criteria, the ranking order is obtained as A ¹ >  A ² >  A 3 >  A 4 . Interval type-2 fuzzy sets have successfully hybridized with TOPSIS and entropy weight in proposing a new result of ranking order.

V. Conclusions

This paper has presented a new approach of interval type-2 fuzzy TOPSIS by appending entropy weight for sub-criteria. A simple modification of entropy weight has been made as to accustom with interval type-2 fuzzy sets. A numerical example has been given to demonstrate the proposed method. The results show the effect of the modification to the ranking order in supplier selection problem. Validation of the method could be further strengthened with various decision making applications.

Step 6: Based on (16) and (17), we can get the positive ideal solution and the negative ideal solution respectively:

A ⁺ = lv⁺ vt vt vt v+ v+ I \^v1 ,^v 2 ,^v 3 ,^v 4 ,^v 5 ,^v 6/

= ( 4.2297,4.4189,4.3569,4.2876,42876,4.0905 )

A "   I v ^,v 2 ^,v 3 ^,v 4 ^,v 5 ^,v 6 )

= ( 4.1480,4.2918,4.2938,4.2413,4.2413,4.0461 )

Step 7: Based on (18) and (19), we can get the distance between each alternative and ideal solution.

Step 8: Using (20), we can get the relative degree of closeness of each alternative with the ideal solution. The results of distance and degree of closeness are presented in Table V

Table 5: Final evaluation of alternatives

	d i	d i	Ci = —d-i— d + i + d - i	Rank
A 1	0.0783	0.1638	0.6766	1
A 2	0.0926	0.1594	0.6325	2
A 3	0.1303	0.1766	0.5754	3
A 4	0.1647	0.0693	0.2960	4

Acknowledgment

This research is supported by the Fundamental Research Grant Scheme, Malaysian Ministry of Higher Education (no. 59243). This support is gratefully acknowledged.