A New Inaccuracy Measure for Fuzzy Sets and its Application in Multi-Criteria Decision Making

• I.    Introduction

  The concept of fuzzy sets proposed by Zadeh [1] in 1965 has gained wide applications in many areas of science and technology e.g. clustering, image processing, decision making etc. because of its capability to model non-statistical imprecision or vague concepts. Fuzziness, a feature of uncertainty, results from the lack of sharp distinction of being or not being a member of the set. The first attempt to quantify the fuzziness was made in 1968 by Zadeh [2], who introduced a probabilistic framework and defined the entropy of a fuzzy event as weighted Shannon entropy [3]. In 1972, De Luca and Termini [4] formulated axioms with which the fuzzy entropy measure should comply and defined a kind of entropy of a fuzzy set based on Shannon’s function.

In 1992, Bhandari and Pal [5] proposed a measure of fuzzy divergence between two fuzzy sets corresponding to Kullback-Leibler’s [6 and 7] measure of divergence. Afterwards, by using the idea of Lin [8], Shang and Jiang [9] introduced a modified version of fuzzy divergence measure proposed in [5].

In 1961, Karridge [10] firstly introduced the idea of inaccuracy measure in information theory as a generalization of Shannon’s entropy. It is normal for an observed (say) distribution to differ from a theoretical distribution of a random variable. Kerridge addressed to the problem of defining an (information theoretic) measure of inaccuracy of the distribution to the standard distribution under reference. According to Kerridge [10], the inaccuracy can be regarded as a measure of quantity of missing information. This has been the probabilistic approach. For uncertain phenomena, to cover non-probabilistic cases, Verma and Sharma [11] defined a measure of inaccuracy in the setting of fuzzy sets theory and studied its applications in multi-criteria decision making under fuzzy environment. There may be rather difficult or extreme cases in which our inaccuracy measure may not applied. In the present communication, to overcome this problem a new fuzzy inaccuracy measure of a fuzzy set with respect to another fuzzy set is proposed. This paper is organized as follows:

In Section 2 some basic definitions related to fuzzy set theory are presented. In Section 3 we introduce a new fuzzy inaccuracy measure of a fuzzy set with respect to another fuzzy set. In Section 4 we study some properties of the proposed fuzzy inaccuracy measure. A weighted fuzzy inaccuracy measure is also defined. In Section 5 a method to solve a multi-criteria decision making problem with the help of weighted fuzzy inaccuracy measure is discussed. Finally, a numerical example is presented to illustrate the procedure of proposed method to solve multi-criteria decision-making and our conclusions are presented in Section 6.

• II.    Preliminiries

In this section, we present some basic concepts related to fuzzy set theory which will be needed in the following analysis.

Definition 1. Fuzzy Set [1] : A fuzzy set A defined in a finite universe of discourse X = { x, , x ₂,..., x„ } is mathematically represented as

A = {( x , М л ( x )) l x ^G X ^}, ⁽¹⁾

where и ( x ) : X ^ [ 0,1 ] is measure of belongingness or degree of membership of an element x е X in A .

Definition 2. Set Operations on FSs [1] : Let FS ( X ) denote the family of all FSs in the universe X , and let A , B е FS ( X ) be two FSs, given by,

A = { x , H A ( x )) | x е X } ,

B = { x, Ив (x)) | x е X }, then following set operations are defined on FSs:

• ⁽ⁱ⁾    A C = {( x ,i - h a ⁽ x )) | x ^е X ^} ;

• (ii)    A A B = { x , И л ( x ) v И в ( x )) | x е X } ;

• (iii)    A U B = { x , и _л ( x ) л и _в ( x ))| x е X } ;

where v , л stand for max. and min. operators, respectively.

De Luca and Termini [4] defined fuzzy entropy for a fuzzy set A corresponding to Shannon [3] entropy as

n

H ( A ) = - ¹ Z n i = 1

И A ^{( x}i ^{) lo} g И A ⁽ x )

_   + ^{( 1 -} и A ⁽ x ^{)) lo} g ^{( 1 -} И A ⁽ x j) .

.  (2)

It may be noted that (5) has some problems. If H A ⁽ x i ) * ^{0 and} И в ^{( x}i ) = ^{0 or} H a ⁽ x i ) * ^{1 and} И в ⁽ x i ) = ¹ , for any x , then I ( A ; B ) becomes infinite.

For example: Let A = { x ,0.4^ } , B = { x ,0.0^ } and C = { x , ,1 } be three fuzzy sets, then

I ( A ; B ) = да and I ( A ; C ) = да .

To overcome above mentioned drawback of fuzzy inaccuracy, in the next section, we propose a new fuzzy inaccuracy measure of a fuzzy set with respect to another fuzzy set.

• III.    A New Fuzzy Inaccuracy Measure

We proceed with following formal definition:

Definition 3: Let A and B be two fuzzy sets defined 1n a finite universe of discourse X = { x , x ₂,..., x_n } having the membership values и ( x ) , i = 1,2,—, n and H ( x ) , i = 1,2,..., n respectively.

We define the measure of inaccuracy of fuzzy set B with respect to fuzzy set A , as

Corresponding to Kullback-Leibler’s [6 and 7] measure of divergence, Bhandari and Pal [5] proposed a fuzzy divergence measure between A and B given by

n k (A; в )=-1Z n i=1

n

D ( A | B ) = ¹ Z n i = 1

и A ⁽ x jlog ^ 4 x 1

И в ⁽ x i )

^{( 1 - И} A ^{( x , ))}

^{+ (1 - И} A ^{( x}i ^))log л------.   „

^{( 1 -} И ⁽ x ))

И л ( x jlog ( ^H A ⁽ x ^{)+ И} в ⁽ x ')

+ ( 1 - И л ( x , )) log ^ ² "  ^H A ⁽ x А ^И - ⁽ x i ¹ )

The K ( A ; B ) , is well defined and is independent of the values of и ( x ) and и ( x ) . From both the definitions of I ( A ; B ) and K ( A ; B ) , it is easy to see that K ( A ; в ) can be described in the terms of I ( A ; B ) as follows

Later, Shang and Jiang [9] pointed out that (3) has a drawback, i.e., when и_в ( x ) approaches 0 or 1, its value tends toward infinity. Therefore, they proposed a modified version of fuzzy divergence measure (3), given as

K ( A ; B ) = 1 1 A ;

A + B ^

2 J

И A ⁽ x jlog

И л ^{( x} J

И A ^{( x}i ^{) +} И в ^{( x} I J

n

J (AB )=Z l=1

^{+ ( 1 -} И л ⁽ x jjlog

^{( 1 -} И л ⁽ x i ))

( Ил ⁽ x i ^{) +} И в ⁽ x )

I        2

. (4)

Recently, Verma and Sharma [11] defined a measure of inaccuracy of fuzzy set B with respect to fuzzy set A , corresponding to Karridge [10] inaccuracy measure as

It is also interesting to note that when A = B , then (6) reduces to (2), the measure of fuzzy entropy given by De Luca and Termini in [4].

Now, again consider above example with measure (6), we get

K ( A ; B ) =1.0627 and K ( A ; C ) =0.9726.

The good part is that the new measure shares properties with measure (5).

n

I ( A ; в ) =- ¹ Z

П i = 1

H A ^{( x}i ^{) lo} g И в ⁽ x i )

_ ^{+ ( 1 -} H A ⁽ x i )) ^lo g ^{( 1 -} И в ⁽ x i )) _ .

IV. Properties of Fuzzy Inaccuracy Measure

K ( A ; B )

The measure of fuzzy inaccuracy defined in (6) has the following properties:

Theorem 1: For A, B e FS ( X ) ,

K ( A ; B ) < 1 [ I ( A ; B ) + H ( a )] .

Proof: Since m ( x. ) > 0and m ( x ) > 0for any x e X , by the inequality of the arithmetic and geometric mean, we have

M a ( x ) log ^{f M} A < + ^M ( ^x > )

+ ( 1 - m a ( x , )) log f ² ~ ^M A ⁽ x )   ^M - ^{( x )} ]

^ Avx^ l^ Blx l > ; m a ( x ) m ( x,)

2 ^, for any x_t e X

The above relation holds only when either

M a ^{( x}, ⁾ = M b ^{( x}, ) = ^{0 or} M a ^{( x}, ) = M b ^{( x}, ⁾ = ¹ for all ^V '' •

Conversely, let either     m ( x ) = M ( x ) = 0

or m ( x ) = Ms ( x ) = 1, this implies

and

2 - _P A ⁽ x )- ^{M (} x ) >^ - ^ A ( x ^ - M b ( x ) ) , (9) for any x_t e X

M ( x ) log ^{f M a (} x H ^{M b ( x , )} j

+ ( 1 - m ( x ) ) log ^f 2- ^M A^^x ) ^{— M} B I x l ^j

= 0, V ,

Thus,

K ( A ; B )

n

=- ¹ z

П , = 1

M a ^{( x}, ^{) lo}g ^f

—

M a ⁽ x )) ^log ^f

2       J

2 - Ma (x, ) — Mb (x,

1 У M a ^{( x}, ^{) lo} g ⁽7 M a ⁽ x ) M B ⁽ x ) )

n ^, = ¹ _ ^{+( 1 -} M a ^{( x}, ^{)) lo} g ⁽7 ^{( 1 -} M a ^{( x}, ^{))( 1 -} M b ^{( x}, )) )_

n

=-—z

2 n ff

M a ⁽ x jlog ⁽ M A ^{( x} M ⁽ x )) _ ^{+( 1 -} M a ^{( x}, ^{)) lo} g ^{(( 1 -} M a ^{( x},

))( 1 — M b ( x J)) J

n

-—z

2 n ^z

(1 - Ma (xJ)

" log ( ^{1 -} M a ( x )) ' _V ⁺ log ( ^{1 -} M b ( x ) ) .

= 1 [ I ( A ; B ) + H ( A )] .

This proves the theorem.

Theorem 2: K ( A ; B ) = 0 if and only if either M a ⁽ x , ) = M b ⁽ x , ) = ^{0 or} M a ⁽ x ) = M b ⁽ x ) = ¹ V , = 1,2,..., n .

Proof: First let K ( A ; B ) = 0 , then

Ma (x, )+ Mb (x,

n

-1 z n ,=1

+ (1 - Ma (x,

2       J

Vl- f ^{2 -} M a ^{( x}, ^)- M b ^{( x},

= 0 (10)

or

K ( A ; B ) = 0.

This proves the theorem.

To prove results given in Theorems ahead, we will consider separation of X into two parts X and X , such that

X , =^{ x I ^{x e} X , M a ^{( x} ) > M b ^{( x} , ) ^} ,                 ⁽¹²⁾

X 2 = { x I x e X , M b ( x ) < M a ( x , )} .                 ⁽¹³⁾

Theorem 3: For A , B , C e FS ( X ) ,

• (i)    K ( A U B ; C ) < K ( A ; C ) + K ( B ; C ) ;

• (ii)    K ( A П B ; C ) < K ( A ; C ) + K ( B ; C ) .

Proof: In the following, we prove only (i), proof of (ii) can be formulated analogously.

(i) Let us consider the following expression

K ( A ; C ) + K ( B ; C ) - K ( A U B ; C )

—

n

¹ z n , = 1

M a ^{( x}, ^{) lo}g ^f

Ma (x)+ Mc (x)

+ (1 - MA (x I

²        J

,f ^{2 -} M a ^{( x}, ^)- M e ^{( x},

n

- ¹ z n , = 1

n

+1 z n ,=1

M b ^{( x}, ) log ^f

M b ^{( x}, ^{) +} M e ^{( x}, )

+ (1 - Mb (x.))logf

( M a ( ^x, )^v M B ( ^x, )) log

(^1-( M a ( ^x, )v M b ( ^x, ))) log

+ Me ( x,) J f 2-( Ma (x, )v Mb (x, )f

_____________ ^- M e ( ^x, )

V

J.

x i E X ₂

M a ( ^xi ) ^log ^r

м Ы+ М Ы

a

n

> 0

⁺

V

r

x i ^{E X} 1

( 1 ^- M a ( x i )i ^log|

2      7

^{2 -} M a ^{( x}i -)^- M c ^{( x}, -)

M b ⁽ x i A'g ^

M b ^{( x}i ⁾⁺ M c ^{( x}i

^{+ ( 1 -} M b ^{( x}, ^{)) lo}g| '

VV

^{2 -} M b ^{( x}i ^)- M c ^{( x}i

Adding (15) and (16) we get the result.

• Theorem 5: For A , B e FS ( X ) ,

• (i)    K ( A ; A U B ) + K ( A ; A П B ) = H ( A ) + K ( A ; B ) ;

• (ii)    K ( B ; A U B ) + K ( B ; Л П B ) = H ( B ) + K ( B ; a ) .

Proof: In the following, we prove only (i), proof of (ii) can be formulated analogously.

(i) Using definition in (6), we first have

K ( A ; л и в )

This proves the theorem.

Theorem 4: For A , B , C e FS ( X ) ,

K ( A U B ; C ) + K ( A П B ; C ) = K ( A ; B ) + K ( A ; C ) .

n n i=1

Proof: From definition in (6), we have

K ( A U B ; C )

⁽ М л ^{( x}i ^{) v} M b ^{( x}i ^{)) lo}g ^r

⁽ M a ⁽ x , ) v M b ⁽ x , )) ⁺ M c ( x i )

M a ( x i ) ^lo g

M a ( ^x. ) ⁺ ( M a ( x i ) ^v M b ( x i ) )

⁺ ( 1 ^- M a ( x i ) ) ^lo g

^{2 -} M a ( ^x i )

^- ( M a ( ^x i ) ^v M b ( ^x, ) )

n

=-1X n  i=1

2            7

Г ^{2 - (} M a ^{( x}i ) ^v M b ⁽ x )) )

M a ( x i ) ^log

M a ( X ) ⁺ M a ( x i )

X xiEX1

—

n

and

^{+ ( 1 -(} M a ⁽ x i ^{) v} M b ⁽ x i ^{))) lo}g

M a ⁽ x, ^{) lo}g l

M A ⁽ x i ) ⁺ M c ⁽ x )

^{+ ( 1 -} M A ⁽ x .

—

V

+X xi E X2

K ( A П B ; C )

n n i=1

n

V

M b ⁽ x i ^{) lo}g [

V

M c ⁽ x i )

A

1 n

X xiE X1

' 2 - M a ( x i P

( 1 ^- M a ( x ) ) ^log

-

M a ( ^xi )

. (17)

)) ^lo g^-

² - M A ⁽ x i ^{) -} M c ⁽ x ,

M в ⁽ x > ■ M c ⁽ x )

^{+ ( 1 -} M b ⁽ x Wop

A

. (15)

+X xi E X2

^{2 -} M в ⁽ x ) ^- M c ^{( x} i

( Ц , ( x. ) л M b (. x i il og SAFXyM B lbb C i xl j

^{Г 2 -(} M a ^{( x}. ^)л M b ^{( x} i )) )

^{+ ( 1 -(} M a ^{( x} i ) ^A M b ^{( x} i )) ^{) lo}g

X xiE X1

Г / V

M b ^{( x}i ^{) lo}g

—

M c ^{( x} i )

V

M a ( x i ) ^log

M a ( x i ) ⁺ M b ( x )

2        7

^{r 2 -} M a ( x , )⁴

⁺ ( 1 ^- M a ( x ) ) ^log

-

M b ( x i )

Next, again from definition in (6), we have

K ( A ; A П в )

M a ( ^x, ) ^log

M a ( ^xi ) ⁺ ( M a ( ^xi P M b ( ^x, ) )

M b ^{( x}i ^{) +} M c ^{( x}i )

_Г ^{+ ( 1 -} M b ^{( x}i ^{)) lo}g[' VV

^{2 -} M b ^{( x}i ) ^- M c ^{( x}i

A

+ X x ^ X 2

Г

M a ( x i ^{) lo}g

²         77

M a ^{( x}i ) ⁺ M c ^{( x}i )

A

. (16)

n

=-1X n i=1

n

⁺ ( 1 ^- M a ( ^xi ) ) ^log

²             J

" ^{2 -} M a ( ^xi )

^- ( M a ( ^xi ) ^A M b ( ^x, ) )

X xiE X1

г

M a

V

M a ⁽ x i ) ⁺ M b ( x i )

V 2

^{+ ( 1 -} M a ( x N

^{2 -} M a ^{( x}i ) ^- M b ^{( x}i

+

V

' ^{2 -} M a ⁽ x i ^{) -} M c ^{( x},

+ X xi E X2

Г Z X. Г M a ^{( x}i ) ^lo g('

M a ^{( x}i ^{) +} M a ^{( x} J

.  (18)

Г

^{+ ( 1 -} M a ( x i ^{)) lo} g| ■

VV

^{2 -} M a ^{( x} J^- M a ^{( x}i

Adding (17) and (18) we get the result.

Theorem 6: For A, B e FS ( X ) , then

Proof: Let us separate X into two parts X and X , such that

K ( A U B ; A A B ) + K ( A A B ; A U B )

= K ( A ; B ) + K ( B ; A ) = 2 H f A + B j "

X , =^{ x | x ^e X , w . ^{( x} ) ^ W c ^{( x} i ) ^} ,                 ⁽²¹⁾

X 2 = { x I x e X , w . ( x ) < W c ( x , )} .               ⁽²²⁾

Proof: By using definition in (6), we first have

K ( A U B ; A A B )

We then have,

K ( A ; B U C )

I " ⁽ x i ^)v W B ⁽ x i ))   '

⁽ W A ⁽ x , ^)v W . ⁽ x i

)) _log ^{+ (} W A ⁽ x , ^)л w . ⁽ x ))

n

=—1 z n i=1

V

^{f 2 — (} W A ⁽ x i ^)v W B ⁽ x JH

n

=—1 z n ITT

W ( x_ ) log ^{f W} A ⁽ x i ^{)+( W} B }x i ^{)v W} C ⁽ x i

^{+ ( 1 — (} W A ⁽ x i ^)v W . ⁽ x i ^{))) lo}g

—

I " ⁽ x , ^)л w . ⁽ x i ))

^{+ ( 1 —} W a ⁽ x i Il log ^

^{2 —} W a ⁽ x i ^{)— (} W b ⁽ x ) ^v W c ⁽ x i

1 n

' W a ( x )_{b s} ( ^W A ⁽ x i ) + ^W B ⁽ x i ) ^j         '

¹ + ( 1 — W a ( X . )) log f ^{2 — W} " ⁽ x^ ^W B ^{( X l} 1

V                V         ^{2         J} J

' W B ( . ^W B ^{( W} A ^{( X ) j}         '

+ ( 1 — W . ( » W ² "  ^W B ⁽ x j' ^W - ⁽ x ) 1

V                   ^{V           2           J}J.

Next, again from definition in (6), we have K ( A A B ; A U B )

⁽ W A ⁽ x i ^)л W b ⁽ x , ^{)) lo}g

⁽ W A ⁽ x i ^)л W b ⁽ x i ))  "

^{+ (} W A ⁽ x i ^)v W b ⁽ x i ))

—

¹ z n i = i

n

^{( 1 — (} W A ⁽ x i ^)л W b ⁽ x i ^{))) lo}g

' W , (_ , .)log [ ^W A ⁽ x i ^{) + W} B ⁽ x i ) ¹            '

¹ + ( 1 — W . ( ! i )) log f ^{2 — W} A ⁽ "^{i )— W} B ^{( x )} 1 V               ^{V         2}         yy

. (23)

n

. (19)

^{2 — (} W A ⁽ x i ^)л W b ⁽ x i F I " ⁽ x i ^)v W b ⁽ x i ))

+ z

x * e X 2

W a ⁽ x i ^{) lo}g^f-

W a ⁽ x i ^{) +} W c ⁽ x i )

^{+ ( 1 —} W a ⁽ x i ^{)) lo}g|- VV

2       J

^{2 —} W a ⁽ x i ^)— W c ⁽ x i )

y

z xie X1

f          f W ( x ,) + Wa ( x , ) 1

W b ⁽ x jlog l    B^v 2 A^v I

+ ( 1 — W b ( X i )) log ^{f 2   W} B ⁽ x )   ^W A ⁽ x* ) ¹

^{V         2         7} J

. (20)

+z xi e X 2

W a ⁽ X ^{) lo}g^f-

W a ^{( x}i ⁾⁺ W b ^{( x}i )

V

^{+ ( 1 —} W a ⁽ X ^{)) lo}g^f-

^{2 —} W a ^{( x}i ^)— W b ^{( x}i )

J

Finally, adding (19) and (20) we get the result.

Theorem 7: For A , B , C e FS ( X ) ,

K ( A ; B U C ) + K ( A ; B A C ) = K ( A ; B ) + K ( A ; C ) .

And

K ( A ; B A C )

—

1 z n i=1

—

n

n

„         f W a ⁽ x i ⁾⁺⁽ W b ⁽ x i ^)л W c ⁽ x i )) 1

^W A ⁽ x i ^{) log}l                  2                  I

+ ( 1 — Wa ( x , )) log f ^{2 — W a (} x i ^{)—( W i (} x i^ ^W C ⁽ x i ))

(

z x, e X!

V

+z xi e X2

W A ⁽ x i ⁾⁺ W c ⁽ x i ) j

2       J

F     ^{f 2 — W} A ⁽ x , ^{)— w} c ⁽ x )

A A      2

^f w . ( x , ) log [ ^W - ^{( x}i ) + ^W B ⁽ x i ) |

V

^{+ ( 1 —} W a ⁽ x i i ^{) lo}g

J

. (24)

^{2 —} W a ⁽ x i ^)— W b ⁽ x i )

J

Adding (23) and (24) we obtain,

K ( A ; B U C ) + K ( A ; B A C ) = K ( A ; B ) + K ( A ; C ) .

This proves the theorem.

Corollary : Let A , B , C e FS ( X ) , then

K ( A ; B U C ) + K ( A ; B A C )

= K ( A U B ; C ) + K ( A A B ; C )            (25)

= K ( A ; B ) + K ( A ; C ) .

Proof: It obvious follows from Theorems 4 and 7.

• Theorem 8: For two fuzzy sets A and B ,

H ( A ) < K ( A ; B ) ,                             (26)

Note: If w = [ —, — ,—,— | , then formula (28) is ( n n n J reduced to formula (6).

with equality if and only if A = B ,  i.e.,

B a ⁽ x ) = B b ⁽ x j ^V x e X .

Proof: Let us consider the following expression

K ( A ; B ) - H ( A ) .

After putting the value of K ( A ; B ) and H ( A ) in (27), we get

B a ⁽ x j log

n

=12

n , = 1

B a ⁽ x )

B a ⁽ x ^{) +} В в ⁽ x )

^{+ ( 1 -} B a ⁽ x )) log

^{( 1 -} B a ⁽ x , )

^{2 -} B a ⁽ x ^)- B b ⁽ x )

= J ( A | B ) .

From [8], we know that J ( A | B ) > 0 with equality if and only if A = B , i.e., в ( x ) = В ( x ) V x e X .

Hence

K (A; B )- H (A )> 0, with equality if and only if A = B ,  i.e.,

B a ⁽ x. ) = B b ⁽ x ) ^V x ^e X .

This proves the theorem. •

Considering that the elements in the universe of discourse X = { x, , x ₂,..., x^ } may have different importance, we define the weighted fuzzy inaccuracy measure of fuzzy set B with respect to fuzzy set A , as

Definition 4: Given two fuzzy sets A and B defined in a finite universe of discourse X = { x, , x ₂,..., x„ } with membership values в ( x ,) and в ( x ) , ^z ' = 1,²,—, n , with weight     vector w = ( w , w ₂,..., w_n ) T    of    the

n elements x , г’ =1,2,...,n , such that w > 0 and 2w = 1, i=1

the weighted fuzzy inaccuracy of fuzzy set B with respect to fuzzy set A , is defined as

K ( A ; B , w )

V. Application to Multi-criteria Decision Making

In many real-life cases, decision makers usually cannot choose but provide their preferences in the form of fuzzy information as a result of vague knowledge about the preference of alternatives. Therefore, a lot of fuzzy multicriteria decision making approaches have been developed and applied to diverse fields, such as engineering, management, economics, and so on. In this section, we present a method to solve multi-criteria decision making problems with the help of weighted fuzzy inaccuracy measure proposed by us.

Let M = { М ,, M ₂,..., M_m } be a set of options, C = { C , C ₂,..., C„ } be a set of criteria with weight vector w = ( w , w ,..., w ) T , where w >  0, ( j = 1,2,..., n )

n and 2 w. = 1. The characteristics of the option M. in j=1

terms of criteria C are represented by the following FSs:

M, ={Cj,В,^ Cj e C}, , = 1,2,...,m and j = 1,2,..., n , where в indicates the degree that the option M satisfies the criterion C .

Using the measure defined by (28), we introduce the following approach to solve the above multi-criteria fuzzy decision making problem:

Step 1: Find out the positive-ideal solution M ⁺ and negative-ideal solution M ^- :

^{M +} = ^{ В 1 + ), ( b _{2 +} ),...,( B n +) ^} ,

M " ={ В1- \ Вв2-),...,(Bn -)}, where, for each j = 1,2,...,n ,

^B bj+}= (max Bj) (Bj -) = (^m i ⁿ Bj)

n

=-2 w i=1

B a ( x , ) log ^ ^{B a (} x - ⁾ + ^B b ⁽^ J

+ ( 1 - B a ( x , )) log ^ ² - ^{B a (} x ₂ ^{)- B} b ^{( x )} J

Step 2: Calculate K ( M ⁺ ; M_ , w ) and K ( M ; M_ , w ) given respectively by the following:

K ( M ⁺ ; M, , w )

. (28)

n

=-2 w j=1

B j + ⁽ x jlog

( B j + ⁺ B j )

I 2 J

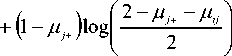
, (30)

And

K ( M, ; M ^- , w )

n

=-E wj j=1

(^ j - + ^ j )

^ j - ⁽ X i ^{) lo}g I j ₂ j I

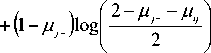
Step 3: Calculate the relative weighted fuzzy inaccuracy measure K ( M , w ) of option M, with respect to M ⁺ and M ^- , where

K ( M + ; M ,., w )

K (M, w) =                  ------Г v i ’  K (M +;M, w) + K (M-;M, w), (32)

i = 1,2,..., m

Step 4: Select the option M_k with smallest K ( M_k , w ) .

• VI.    A Numerical Example

In order to demonstrate the applicability of the proposed method to multi-criteria decision making, we consider below an investment company decision-making problem.

Example: Suppose that an investment company wants to invest a certain amount of money in the best option out of five options: A car company M , a food company M , a computer company M , an arms company M and a TV company M . The investment company needs to take a decision according to the following four criteria: (1) G is the risk analysis (2) G is the growth analysis (3) G is the social-political impact analysis (4) G is the environmental impact analysis. Let w = (0.20,0.18,0.32,0.30)T be the criteria weight vector. The five possible options M (i = 1,2,...,m) are to be evaluated by the decision maker under the above four criteria in the following form:

M 1 = { G 1 ,0.5\( G 2 ,0.6), ( G 3 ,0.3), G 4 4 ,0.2) } ,

M 2 = { G ₁,0.7), G 2 ,0.7), ( G 3 ,0.7), ( G 4 ,0.4) } ,

M 3 = { G 1 ,0.6), ( G 2 ,0.5), ( G , ,0.5), ( G 4 ,0.6) } ,

M 4 = { G 1 ,0.8), ( G 2 ,0.6), ( G 3 ,0.3), G 4 ,0.2) } ,

M ₅ = { G 1 ,0.6), G 2 ,0.4), ^,0.7), ( G 4 ,0.5) } .

By step 1, we obtain the positive-ideal solution M ⁺ and the negative ideal solution M ^- :

M⁺ = { G 1 ,0.8), ( G 2 ,0.7), G 3 ,0.7), ( G 4 ,0.6) } ,

M - = { G 1 ,0.5), ( G ₂,0.4), G 3 ,0.3), G 4 ,0.2) } .

By step 2, we use formulas (30) and (31) to measure K ( M ⁺ ; M_t , w ) and K ( M ^- ; M_t , w ) , respectively, we get the following tables:

Table 1: Values of K ( M ⁺ ; M_t , w )

K ( M +; M ,, w )	0.8662
K ( M +; M 2, w )	0.7457
K ( M +; M 3, w )	0.7685
K ( M +; M 4 , w )	0.8407
K ( M +; M 5, w )	0.7642

Table 2: Values of K ( M ; M_t , w )

K ( M ~; M ,, w )	0.7557
K ( M ~; M 2, w )	0.7547
K ( M ~; M 3, w )	0.7569
K ( M - ; M 4, w )	0.7535
K ( M ~; M 5, w )	0.7620

By step 3, we obtain the relative weighted fuzzy inaccuracy measure K ( M , w ) of option M, with respect to M ⁺ and M ^- by using the formula (32). We get the following table:

Table 3: Values of K ( M_t , w )

K ( M„ w )	0.5341
K ( M 2 , w )	0.4970
K ( M 3 , w )	0.5038
K ( M 4 , w )	0.5273
K ( M 5 , w )	0.5007

Table 3 shows that the ranking order of five options is:

M ₂ ^ M ₅ ^ M ₃ ^ M ₄ ^ M ,.

Thus M is the most desirable option.

• VII.    Conclusions

In this work we have proposed a new fuzzy inaccuracy measure to measure the inaccuracy of a fuzzy set with respect to another fuzzy set. This measure is a modified version of fuzzy inaccuracy proposed by Verma and Sharma [11]. Some properties of the new fuzzy inaccuracy measure are investigated in detail. Furthermore, based on the weighted fuzzy inaccuracy, an approach to deal with multi-criteria decision-making problems under fuzzy environments is developed. Finally, an example is provided to illustrate the multicriteria decision-making process.