A New Joint Possibility Data Association Algorithm Avoiding Track Coalescence

Published Online March 2011 in MECS

Joint Probabilistic Data Association (JPDA) algorithm [1] is usually used to solve the problem of tracking multiple targets under the environment of heavy clutter. But the traditional JPDA algorithm will cause track coalescence when the targets are parallel neighboring or small-angle crossing. The adjacent tracks will be attracted by each other and gradually change to be coalescent in above scenarios. The main reason of this phenomenon is that the adjacent targets may share the same measurement as their main measurement in the JPDA algorithm.

The Exact Nearest Neighbor Probabilistic Data Association (EN-NPDA) algorithm has shown that associated events pruning may be an effective way to prevent track coalescence. EN-NPDA [2] involves the enumeration of all peak-to-target association hypotheses as JPDA, but only the most likely hypothesis is retained. While this approach inhibits compound coalescence, it was found to lead to track over commitment and an increased incidence of track divergence in the presence of clutter and absent target detections. Most of the modified

The work of Song-lin Chen was sponsored by Natural Science Foundation of Shanxi Province: S2011JC5766.

JPDA algorithms avoiding track coalescence by means of appropriately pruning associated events or using a scaling factor to produce a new algorithm whose effect ranging between EN-NPDA and JPDA algorithm. The paper [3] proposed a Scaled JPDA (SJPDA) algorithm which introduced a scale factor. When the scale factor value is infinity, the algorithm is equivalent to the EN-NPDA algorithm. And when the scale factor value is one, the algorithm is equivalent to the JPDA algorithm. So when the scale factor value is an appropriate intermediate value, the SPDA algorithm not only can avoid track coalescence, but also can control track divergence in the presence of clutter and absent target detections. But the scale factor comes from the experience.

In this paper, a K Nearest Neighbor Joint Probabilistic Data Association (KNNJPDA) algorithm is proposed. Through the Monte Carlo simulations, track coalescence is avoided and significantly improved efficiency is shown when the KNNJPDA algorithm is used to track targets.

The paper is organized as follows. Target and measurement models are described in Section II, and the steps of the JPDA algorithm are described in Section III, the Principle and Steps of the Modified JPDA Algorithm are described in Section IV. Section V presents simulations that demonstrate the effectiveness of this approach, and conclusions are given in Section VI.

• II.    T ARGET AND M EASUREMENT M ODELS

We consider c targets in single sensor system, the target states and measurements in the next time interval can be predicted by x (k) = F* (k -1)x (k -1) + V (k -1),      (1)

z j ( k ) = H ( k ) x * ( k ) + w ( k ),             ⁽²⁾

Where xt (k) is the n-dimensional state of the target at time k; F* (k -1) is state transition matrix; V (k -1)is a process noise vector which follows the multivariate normal distribution, N(0; Q) , where N denotes Gaussian distribution, and Q is the covariance matrix of the process noise vector, H(k) is the measurement matrix, w(k) is the measurement noise vector which is assumed to follow the multivariate normal distribution, N(0; R), where R is the covariance matrix of the measurement noise vector.

Let Z ( k ) be the set of measurement vectors at frame k :

Z ( k ) = { Z , ( k ), Z 2 ( k ),..., Zm_t ( к )} ,        (3)

m _k is the number of measurement vectors at time k .

• III.    S TEPS OF THE JPDA A LGORITHM

JPDA is a multi-target extension of Probabilistic Data Association [4-6] which considers each track in isolation. It takes into account the fact that a measurement may fall inside the intersection of two or more validation gates of several different targets and so could have originated from any of these targets or from clutter.

Step 1: Target state initialization :

x ˆ ^t (00) ， P^t (00)are the initial state vector and covariance, which are given by system.

Step 2: Computing the state and covariance prediction : x * ( k\k - 1) = F* ( k - 1) x * ( k - 1| k - 1),       (4)

P ( kk -1) = F * ( k -1) P ( k -1 k -1)[ F t ( k - 1)] ^T + Q ( k -1), (5)

Step 3: Affirming validation measurements :

Z_k ^t is the set of validation measurements which originate from target t at time k [7]. It follows

Zk={zj(k) dk ^ Y, j=u., mk}

• ²_ j,i                 Л"]^-1-.

dk = vt(k) LS (k)] v* (k),

Where y is the gating size, v * ( k ) is the measurement residual and S_t^j ( k ) is the residual covariance.

v/ (k) = zj (k) - H (k) x* (k|k -1),(8)

S*(k) = H(k)P*(k\k -1)H(k)T,(9)

Step 4: Generating the validation matrix and the feasible matrix :

The validation matrix which is defined as follows:

Q = L^j*],i = 1,2,...,mk;* = 1,2,...,c,(10)

Where to j* is binary element, and to j* = 1 stands for the measurement j lies in the validation gate of the target t . Index * = 0 stands for “no target.” and the corresponding column of Q has all units-each measurement could have originated from clutter or false alarm. m _k is the number of the validation measurements and c is the number of the targets.

After generating validation matrix, we will split validation matrix to generate feasible matrices, which must follow two principles:

• a)    There is only one nonzero element in every row of feasible matrix after splitting validation matrix;

• b)    There is not more than one nonzero element in every column of feasible except the first column.

Each joint event 0 i can be represented by a feasible matrix.

Q (9P = [ to, ( 3 )] ,            (11)

It consists of the units in Q corresponding to the associations assumed in event 0 i .

Step 5: Computing association probabilities :

n _k

P j* = Z P {⁰\z^k to ( 3 ),         ⁽¹²⁾

i = 1

Where p { 0i| z k } is the probability of the joint feasible event, Z ^k is the set of all validation measurements.

• 1    ^„ c 3

« > ,* ( 3 i ) = ² j* i ,            ⁽¹³⁾

[ 0 o*herwise

Where 3 j* stands for the association event that Z j ( k ) originate from target t .

Step 6: State estimate :

The state vectors x ˆ ^t ( kk ) and the covariance matrices P^t ( kk ) of the targets are updated as

5c * ( k\k ) = x * ( k\k - 1) + K ( k ) ^ p j*" v *j ( k ) , (14) ^j

P ( k\k ) = P ( k| k - 1) - (1 - p _{0 1} " ) K * ( k ) S * ( k ) K * ( k ) ^T

+ K ( k ){ ^ в _у*" vv j ( k ) vv j ( k ) ^T - Z P j*' v j ( k )L Z P j*" v j ( k )] ^T } K * ( k ) T , j    jj

K * ( k ) = P * ( k\k - 1) H ( k )[ S * ( k )] ^{- 1},        (16)

Set k=k+1 , and go to Step 2.

• IV.    P RINCIPLE AND S TEPS OF THE M ODIFIED JPDA A LGORITHM

• A. Principle of the Modified JPDA Algorithm

The association possibilities of the target with every measurement will be computed in the KNNJPDA algorithm, but only the first K measurements whose association probabilities with the target are larger than others’ are used to estimate target’s state. When K=1, the new algorithm is equivalent to the EN-NPDA algorithm. And when K is given a large value, the algorithm is equivalent to the JPDA algorithm. So when K is given an appropriate intermediate value, the new algorithm not only can avoid track coalescence, but also can prevent track divergence in the presence of clutter and absent target detections.

In SJPDA algorithm, an arbitrary positive scaling factor is introduced to multiply the maximum probabilities of every target associated with measurements. The scaling factor ranges from one to infinity. When the scale factor value is infinity, the algorithm is equivalent to the EN-NPDA algorithm. And when the scale factor value is one, the algorithm is equivalent to the JPDA algorithm. When the scale factor value is an appropriate intermediate value, the SJPDA algorithm can avoid track coalescence, and track divergence can be controlled slightly too.

B. Steps of the Modified JPDA Algorithm

Comparing with the traditional JPDA algorithm, the KNNJPDA algorithm adds one step: Association event pruning.

Step: Association event pruning

Comparing the association probabilities of a target with every measurement, the first K measurements whose association probabilities with the target are larger than others’ are looked as the last validation measurements of

factor must come from the experience. Through simulation test, the best tracking performance can be won when 300 s factor S 800.

V. S IMULATION T EST

A. S mulat on Scenar o Sett ngs

the target. For example, assuming that P_1v в ₂₁,..., в 1 is the association probabilities of target 1 with every measurement and в , >  в .. > ...> в ,       ,

11       21               m_k 1

Z i ( k ), z ₂( k ),..., Z k ( k ) corresponding в _п, P zp-» P k i ^wil l be looked as the last validation measurements of target 1 and P ( K ₊ 1)1 , P ( K + 2)1 ,..., P m_k 1 will be set at 0.

After pruning the association events, the association probabilities of each target with measurements are normalized.

In case of two targets, we respectively use the JPDA algorithm and the KNNJPDA algorithm to track flight target a and target b in the cluttered environment. Two targets stay at constant velocity. Sampling cycle T is 1 second, and gating size γ is 10, 60 sampling points for each target. There are 6 clutters coming into the targets’ associated gates at a sample on the average.

F ( T ) =

T

T

Q ( t ) =

Д> ' = - j •           (17)

Z в , j = 1

This step will be added before the sixth step in the JPDA algorithm.

Comparing with the traditional JPDA algorithm, the SJPDA algorithm also adds one step: Multiplying the Scaled factor.

Step: Multiplying the Scaled factor

Finding out the maximum probability measurement associated with the target.

Assuming that p r 1 = max в , p r 2 = _max p  v,

¹       1 S j S m k               ²       1S j s m k j

Pc = max в , so zri (k) , z (k) ,^, zr (k) are c      1S j s mk j                    1                 2                        c respectively the exclusive measurements of target 1, target 2,…,target c.

A factor is used to multiply the maximum probabilities of every target associated with measurements. The value of the factor ranges from one to infinity.

в _г 1 = factor x P _{t 1} , i = 1,2,..., c ,1S factor S+да ,(18)

This step will be added before the sixth step in the JPDA algorithm too. In Scaled JPDA algorithm, the scale

H (k) =

Г ^T 2/2

T

_ 0

°!

,

°

T ² 2

T

,

Parallel neighboring scenario (scenario 1) : Target a and b flight from southwest to northeast in parallel. The initial positions are (0,0) and (0,600), x velocities of two targets are 300 m/s , the mean error of measurement is 300 meters, y velocities of two targets are 100 m/s , the mean error of measurement is 100 meters.

Small-angle crossing scenario (scenario 2) : The initial positions of target a and b are respectively (0,0) and (0,600), x velocity of a target is 300 m/s , the mean error of measurement is 300 meters, y velocity of a target is 0 m/s , the mean error of measurement is 100 meters. The x velocity of b target is 300 m/s, the mean error of measurement is 300 meters, y velocity of b target is -50 m/s , the mean error of measurement is 100 meters.

B. S mulat on Results and Analys s Compar son Results and D scuss on

We use the JPDA algorithm to track flight targets for 50 Monte Carlo runs in scenario 1 and 2, the simulation results as follows:

x/m

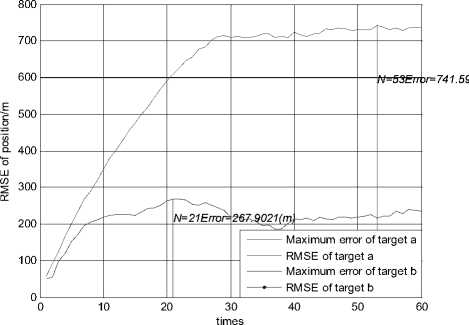
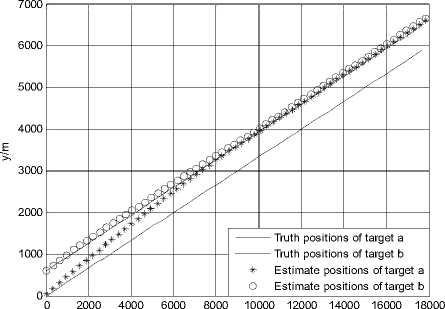
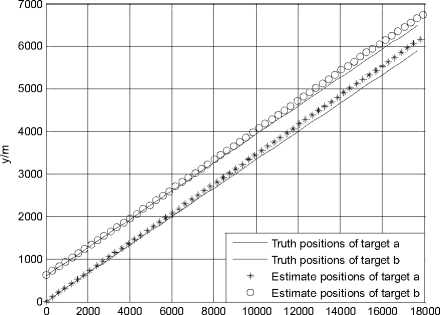
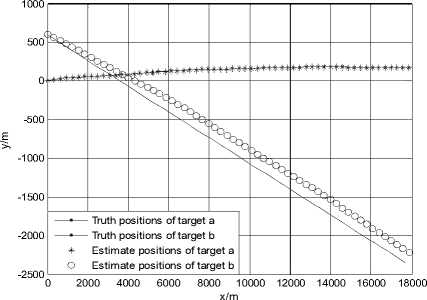
Figure 1.Trajectories of two targets using JPDA in scenario 1

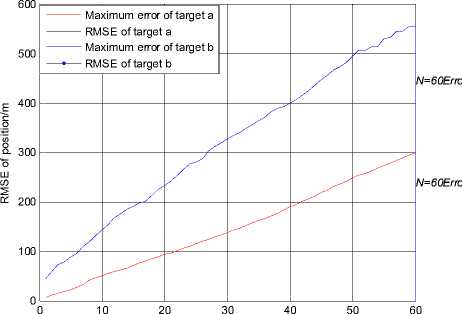
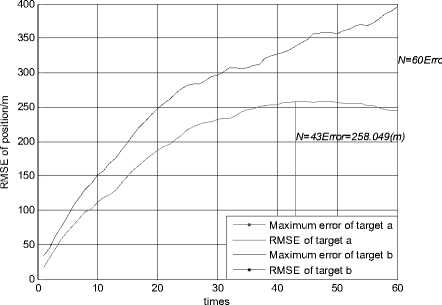
Figure 2.RMSE of position using JPDA in scenario 1

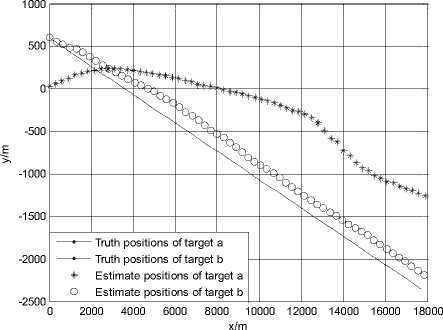
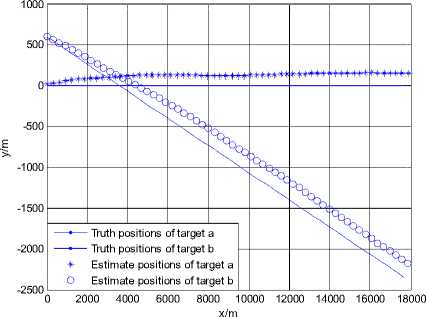
Figure 3.Trajectories of two targets using JPDA in scenario 2

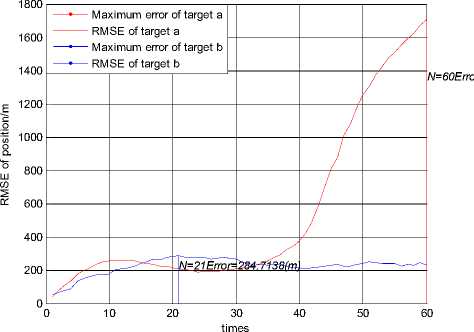
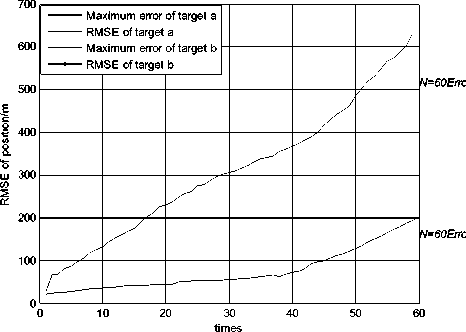
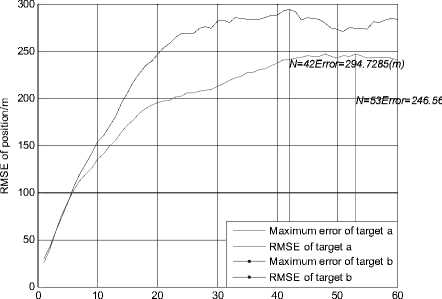
Figure 4.RMSE of position using JPDA in scenario 2

Fig. 3 and Fig. 4 show the simulation result using the JPDA algorithm in scenario 2. In Fig. 3, the trajectory of target a always tends to close with the trajectory of target b . The position RMSE of target a gradually changes to be very large after the 30 seconds. It is shown that track coalescence will be caused using the JPDA algorithm in the small-angle crossing scenario.

Fig. 1 and Fig. 2 show the trajectories of two targets and the root mean squared error (RMSE) of position using the JPDA algorithm in scenario 1. The tracks of two targets gradually merge together and serious track coalescence happens in Fig. 1. The position RMSE of target a is very large in Fig. 2 and the maximum position error of target a is close to 800 m. So we can see that track coalescence will be caused using the JPDA algorithm in the parallel neighboring scenario.

times

Figure 5.Trajectories of two targets using SJPDA in scenario 1( f _{actor =}

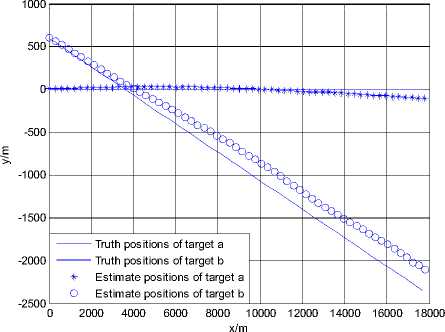
Figure 6.RMSE of position using SJPDA in scenario 1( factor ₌ 300 )

f igure 7.t rajectories of two targets using sjpda in scenario 2( f _{actor =} 300 ) f igure 8.rmse of position using sjpda in scenario 2( factor ₌ 300 )

Then, we use the SJPDA algorithm to track flight targets for 50 Monte Carlo runs in scenario 1 and 2. Fig. 5 and Fig. 6 respectively show the trajectories of two targets and the root mean squared error (RMSE) of position using the SJPDA algorithm in scenario 1( factor = 300). Comparing Fig. 5 with Fig. 1, we can see that the track coalescence is controlled in Fig. 5. At the same time, the position RMSE of target a is very small, but the position RMSE of target b is very large in Fig. 6. It is shown that the SJPDA algorithm can avoid track coalescence, but track divergence can’t be totally prevented using the SJPDA algorithm in the small-angle crossing scenario.

Fig. 7 and Fig. 8 respectively show the trajectories of two targets and the root mean squared error (RMSE) of position using the SJPDA algorithm in scenario 2( factor = 300). In this case, we can see that the track coalescence can be also avoided by the SJPDA algorithm, but the trajectory of target b deviates from the real track and the tracking error is large.

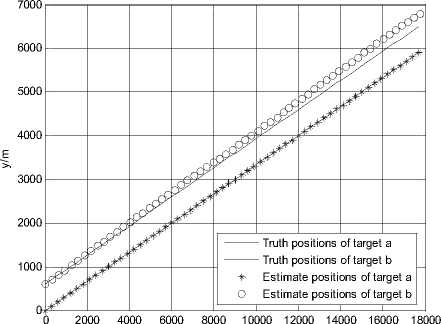
x/m

Figure 9.Trajectories of two targets using KNNJPDA in scenario 1(K=1)

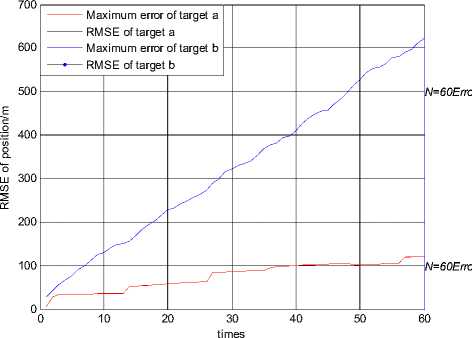
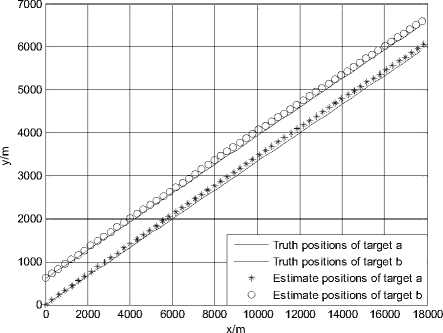
Figure 11.Trajectories of two targets using KNNJPDA in scenario 1(K=2)

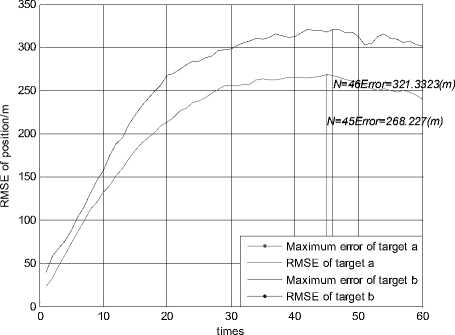
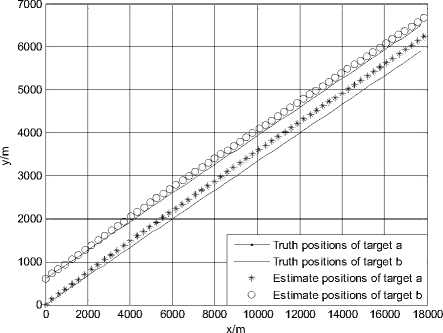
Figure 13.Trajectories of two targets using KNNJPDA in scenario 1(K=3)

times

Fig. 9 and Fig. 10 show the trajectories of two targets and the root mean squared error (RMSE) of position using the KNNJPDA algorithm (K=1) in scenario 1. It is shown that track coalescence is avoided in this case but the trajectory of target b deviates severely from the real track. This simulation result is similar to the simulation result of ENNPDA.

When K=2, the simulation result of the KNNJPDA algorithm is shown in Fig 11 and Fig 12. The tracks don’t merge together in Fig. 11. In Fig. 12 the estimated position errors of two targets are small. It can be confirmed that the KNNJPDA algorithm (K=2) can avoid track coalescence, and ensure very good track precision in scenario 1.

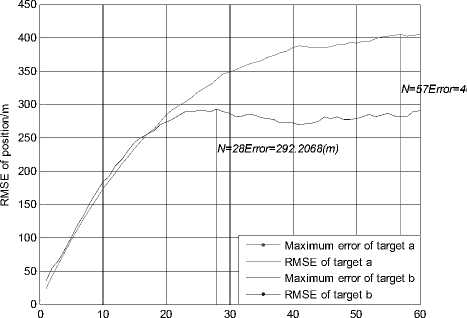
When K=3, the simulation result of the KNNJPDA algorithm is shown in Fig. 13 and Fig. 14. Slight track coalescence appears in Fig. 13 and the RMSE of target a in Fig. 14 is larger than it’s in Fig. 12. In fact, if K is given bigger value, track coalescence will be more serious and the RMSE of target a will be larger. When K ≥ 5, the simulation result of the KNNJPDA algorithm will be similar to JPDA’s.

Comparing Fig. 11 and Fig. 12 with Fig. 5 and Fig. 6, we can see that the tracking precision of KNNJPDA is better than SJPDA’s in the parallel neighboring scenario.

x/m

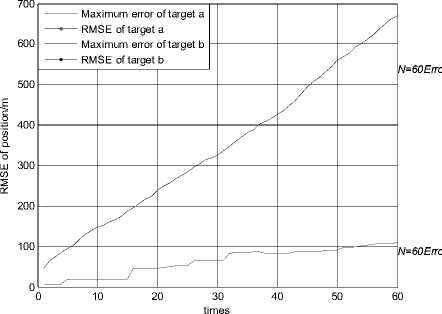
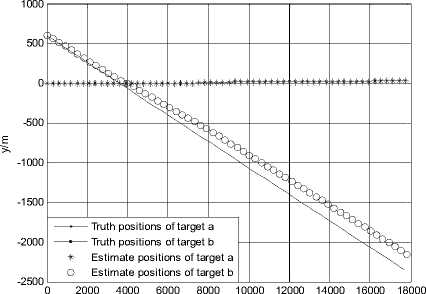
Figure 15.Trajectories of two targets using KNNJPDA in scenario 2(K=1)

times

The simulation results of the KNNJPDA algorithm in scenario 2 are shown in Fig. 15-20. When K=1, the simulation result of the KNNJPDA algorithm is shown in Fig. 15 and Fig. 16. It can be seen that track coalescence is avoided in this case but the trajectory of target b deviates severely from the real track and track divergence is caused.

When K=2, the simulation result of the new algorithm is shown in Fig. 17 and Fig. 18. Comparing Fig. 16 with Fig. 18, the position RMSE of target b in Fig. 18 is smaller than the position RMSE of target b in Fig. 16. It is confirmed that track divergence is controlled by the KNNJPDA algorithm when K=2.

When K=3, the simulation result in the same case is shown in Fig. 19 and Fig. 20. It’s shown that track coalescence is avoided and the new algorithm ensures very good track precision in this case. In fact, when K=4,5,6, the simulation result of the KNNJPDA algorithm is similar to the simulation result when K=3. When K ≥ 7, the simulation result of the KNNJPDA algorithm will be similar to JPDA’s.

Comparing Fig. 19 and Fig. 20 with Fig. 7 and Fig. 8, we can see that the tracking precision of KNNJPDA is also better than JPDA’s in the small-angle crossing scenario.

In addition, the time of the SJPDA algorithm for 50 Monte Carlo simulation runs is approximately 34.38s in scenario 1, and the time of the KNNJPDA algorithm for 50 MC simulation runs is approximately 27.66s in the same case. Thus we can see that the computation of SJPDA is bigger than KNNJPDA’s.

• V.    C ONCLUSIONS

In this paper, a KNNJPDA algorithm has been proposed and implemented. The association possibilities of the target with every measurement will be computed in the new algorithm, but only the first K measurements whose association probabilities with the target are larger than others’ are used to estimate target’s state. The results of simulation test show that, when K=2 or K=3, the new algorithm can avoid track coalescence and ensure good precision in all scenarios. When K=1, the new algorithm is equivalent to the ENNPDA algorithm and track divergence can’t be avoided in the presence of clutter. In parallel neighboring scenario, the best track precision can be achieved using the new algorithm when K=2, and the track effect of the new algorithm is similar to JPDA’s when K ≥ 5. In small-angle crossing scenario, the best track precision can be achieved using the new algorithm when K=3,4,5,6, and the track effect of the new algorithm is similar to JPDA’s when K ≥ 7.

In addition, the simulation results of SJPDA have been predicted in this paper. Through comparing the SJPDA’s simulation results with the KNNJPDA’s, it has been confirmed that two algorithms all can avoid track coalescence but the performances of the KNNJPDA algorithm in tracking precision and computation are better than SJPDA’s.