A new quantum tunneling particle swarm optimization algorithm for training feedforward neural networks

Published Online November 2018 in MECS

Artificial Neural Networks (ANNs) are computational models inspired by the human brain and have been successfully applied to a wide range of pattern recognition, function approximation, classification and nonlinear regression problems [1]. A feedforward neural network is an inter connection of neurons arranged in layers. It consists of an input layer, an output layer and zero or more hidden layers. The input layers and the subsequent layers are connected by links with weights. The strength of the link depends on the weight of the link. The performance of the neural network depends on the number of neurons in each layer and also the weights [1].

Training a neural network involves using an optimization algorithm to compute the weights thereby minimizing the mean squared error between the targets and actual network outputs [2]. Traditionally gradient descent based optimization schemes have been used to train neural networks. Due to the local and deterministic nature of the search performed by gradient based schemes the problem of convergence to a local minima near the initial random starting point is always an issue. Further the ANN error function is nonconvex and highly multimodal and finding the global minimum is a NP complete problem and exact solution is not practical [3]. Thus heuristic global optimization algorithms that compute a good local minimum for neural network training are of interest.

• II.    R elated W ork

In “Iris recognition using artificial neural networks” [4] the authors trained a feedforward neural network with Backpropagation (BP) algorithm for iris recognition. Backpropogation algorithm is a deterministic local search algorithm that converges to a local minimum close to the randomly chosen initial solution. The cost function is the average of the difference between the target and the neural network’s output over all the training samples. BP works in two phases. In the first phase, a forward pass calculates the network’s output for the randomly chosen weights. The error function then determines the error obtained by the network for the chosen weights and biases. The calculated error is then propagated backwards from the output layer to the hidden layers in the second phase. The weights are then adjusted to reduce the error [5, 6]. Since BP uses simple gradient descent to train ANNs it is very efficient but suffers from two fundamental limitations. The learning time taken by the neural network increases with the increase in the size of the data. Since the weight update is proportional to the gradient in BP it does not perform well in the flat regions of the search space where the gradient is almost zero [7]. Biologically inspired optimization algorithms like Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) on the other hand perform a random search and have the ability to escape from local minimum and locate a good approximation to the global minimum [8]. Thus training ANNs with stochastic global optimization algorithms which explore multiple local minima like GA and PSO can be advantageous because of the possibility of locating deep local minima compared to deterministic gradient based algorithms.

GA is inspired by natural evolution and employs selection, crossover and mutation operations to refine an initial random population [9]. It is stochastic and derivative free and can be applied to both continuous and discrete optimization problems [10]. Different variants of the GA have been used to calculate the weights of the feedforward neural network. GA with crossover was used to train ANN in “Improvement of Real-valued Genetic Algorithm and Performance Study” by [11]. A new distributed GA reinforced by perceptron learning rule was used in “Design architectures and training of neural networks with a distributed genetic algorithm” [12], whereas a variation of GA known as soft algorithm which combines GA with backpropogation was used to train ANNs by Adawy et.al., in “A SOFT-backpropagation algorithm for training neural networks”[6]. Application of a parallel implementation of the GA for training feedforward neural networks was explored in [13]. The limitations of GA include slow convergence to the optimum solution; use of complex constructs such as crossover, mutation and selection and the use of large number of adjustable parameters that determine the performance of the algorithm.

The PSO algorithm which is inspired by the social behaviour of a flock of birds was used for training neural networks by Gudise et al. in “Comparison of particle swarm optimization and backpropagation as training algorithms for neural networks” [14]. PSO algorithm is stochastic and derivative free algorithm like GA. However, it does not use complex constructs such as crossover, selection and mutation. It involves interactions between a population of agents with their environment as well as each other [15]. The interaction of agents are constrained using very simple rules. The interaction between the particles results in complex behaviour and emergence of a collective intelligence and problem solving ability.

The performance of the PSO algorithm was compared with the backpropogation algorithm on benchmark nonlinear function approximation tasks by Gudise et.al. It was found that the PSO was the faster of the two algorithms for function approximation tasks as it required smaller computational effort to attain the same error goal. PSO algorithm itself has certain limits in terms of convergence, precision and parameter selection [14]. The algorithm converges prematurely to a local minimum thereby produced lower precision. Therefore in “A novel hybrid Evolutionary Algorithm based on PSO and AFSA for feedforward neural network training” [16] Chen proposed an algorithm called Artificial Fish Swarm Algorithm (AFSA) - PSO parallel hybrid evolutionary algorithm (APPHE) for training feedforward neural networks. The authors tested the performance of the proposed APPHE algorithm with the Levenberg-Marquardt Back propagation (LMBP) algorithm by training the neural network for iris data classification. The neural network trained using the APPHE algorithm did better than LMBP in terms of faster convergence to the good local minimum and accuracy of the result [17].

The explorative ability of the classical particle swarm optimization (PSO) algorithm is reduced because the value of the cost function at the location of the personal best solution found by each particle cannot increase. In this paper a new PSO algorithm inspired by the quantum tunneling in which the personal best solution of each particle is allowed to tunnel through hills in the cost function analogous to the quantum tunneling effect in Quantum Physics is proposed. The introduction of the quantum tunneling effect increases the explorative ability of the PSO algorithm and prevents premature convergence to local minima.

The paper is organized as follows: first the mathematical formulation of the problem is presented, secondly heuristic algorithms for global nonlinear optimization are discussed, thirdly a new PSO algorithm with enhanced exploration ability inspired by the tunneling phenomenon in Quantum Physics is proposed and finally the performance of the proposed algorithm is compared to three state-of-the-art PSO algorithms on benchmark neural network function approximation problems.

• III.    P roblem F ormulation

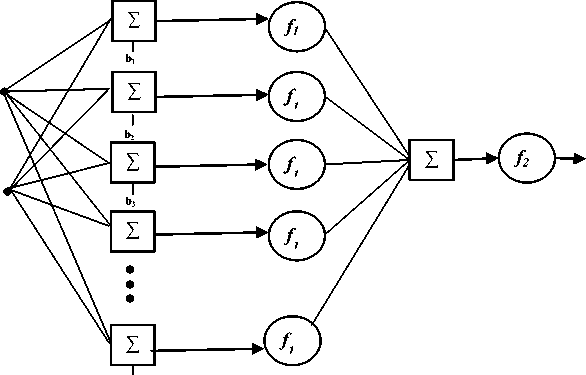
A feedforward neural network is a biologically inspired computation model that consists of a large number of processing nodes called neurons which are interconnected in layers [1, 2]. In a feedforward neural network, the information flows in one direction and does not support feedback. Therefore it is referred to as a feedforward neural network. Every neuron in a layer is connected with all the neurons in the previous layer. These interconnections have different strengths called weights. The weights help in encoding the knowledge of the neural network. The weights of these interconnections can be adjusted by a learning algorithm in order to match the desired output (target). A multi- layer perceptron with adequate number of neurons and one hidden layer can approximate any nonlinear function [1]. Fig. 1 shows the architecture of a feedforward neural network with one hidden layer, two inputs and one output neuron.In supervised learning the input pattern is given to the neurons in the input layer along with the expected output [2]. Each neuron computes the product of the interconnection weights and the input and adds it with the bias and presents the output to a transfer function. The the target output. output generated by the neural network is compared with

X

Y

Z b10

Fig.1. A feedforward ANN with one hidden layer, two inputs and one output neuron. f1 and f2 are tansig and purelin activation functions respectively.

In supervised learning, the learning is done with input and output pairs in the form of (X ⁱ , Yⁱ ) , Where i = 1 to N, ‘N’ the number of training samples, X ⁱ is the input vector X for the i^th training sample and Y ⁱ is the target output for the i^th training sample. Let h ( Xⁱ ) be the neural network output for an input X ⁱ and Ɵ is the activation function. The network’s output is presented in (1)

k h (X ⁱ ) = θ ( ∑ W ij X j + b j )            (1)

i = 1

where W is the weight of the interconnection between i^th neuron and the j^th neuron; b j is the bias of the j^th neuron. The mean square error can be calculated as follows

N

∑ ( Yⁱ - h ( Xⁱ ))²

E ( W ) = ^{i = 1}                             (2)

Equation (2) defines the cost function that measures the difference between the ANN outputs and targets for a given data set. The weights of the ANN are determined by minimizing the cost function with respect to the weights. Because each neuron applies a nonlinear function to its weighted input to calculate its output the overall function h (x) calculated by the neural network and hence the error function E (W) are highly nonlinear. Thus the problem of training the weights of an ANN is a nonlinear global optimization problem of great importance. In this paper a new heuristic global optimization algorithm is proposed and applied to the problem of training feedforward neural networks.

• IV.    G lobal O ptimization

The goal in optimization is to minimize or maximize a real valued function by choosing the best solution from an available set of candidate solutions [18]. Solutions that satisfy the constraints are termed as feasible solutions. In the case of minimization of the ANN cost function the goal is to determine the value of the variables (weights) which minimizes the function [11, 19]. An optimization problem can be formulated as follows min f(x)

Subject to x ∈Ω

Where f : Rⁿ → R is the function that is to be minimized and n is the dimensionality of the vector x . The set Ω is a subset of Rⁿ . The optimization problem above can be viewed as finding the vector x ^* from the domain Ω such that that f ( x ^*) ≤ f ( x ) . A point x ^* ∈Ω is a local minimum of f over Ω if there exists ε > 0 such that f ( x ^* ) ≤ f ( x ) for all x ∈Ω \ { x ^* } and II x - x ^*II < ε .On the other hand a point A point x ^* ∈Ω is a global minimum of f over Ω if f ( x ^*) ≤ f ( x ) for all x ∈Ω . In general, it is only practical to compute a good local minimum as the problem of nonlinear global optimization is known to be NP-complete.

Optimization problems can be unimodal or multimodal [20]. A function is unimodal if it has one local minimum which is also the global minimum. Multimodal functions on the other hand may contain numerous local minima which makes the problem of locating the global minimum either very difficult or impossible. In many instances optimization algorithms get stuck in local minima without converging to the global minimum. Thus only good local minimum can be computed in general. However a majority of important problems like training a neural network involves multimodal global optimization. Hence, heuristic random search algorithms inspired by biology like PSO and GA which can compute approximate optimal solutions are of interest [3].

• V.    P article S warm O ptimization A lgorithm

Eberhart and Kennedy proposed the PSO algorithm inspired by the swarm behavior of a flock of birds and a school of fishes [15]. It has been shown to outperform other global optimization algorithms like the GAs [15, 16]. PSO algorithms starts with a randomly generated population referred to as a swarm which move around the search space [21, 22]. Each generated particle computes its best solution. The particle moves in the direction of the best solution found by it and also the best solution found by the entire swarm of particles. The personal best solution is referred to as pbest and the best solution determined by the swarm is termed as gbest.

In the PSO algorithm every generated particle moves towards the best position found by that particle so far and the best position found by the entire group swarm of particles [15]. The formula for the PSO algorithm is given in (3) and (4).

Vel ( j + 1) = Vel‘ ( j ) + ф ( P ( j ) - X ( j )) +

Ф 2 d ( G d ( j ) - X i 'j j )) (3)

X i ( j + 1) = X( j ) = Vel(j + 1) (4)

where Vel = [Vel ' , Vel i ...Vel‘_N ] denotes the velocity of the particle i; X i = [X ' , X ' ... X *_N ] denotes the position of particle i ; Ф_ы and Ф_м are random numbers which are uniformly distributed P i = [ P i , P i ... P ' ] is the best position determined by the particle i, G = [ G_x , G₂...G_N ] is the best position discovered by the whole group of particles. Dimension of the search space is denoted by N and j is the iteration number. The global best solution of the swarm is updated with the position X if the value of f ( X ) <  f ( G ) [23, 24].

Numerous variants of the classical PSO algorithm have been proposed and applied to various problems. A variant of the PSO called CLPSO (Comprehensive Learning Particle Swarm Optimization Algorithm) was proposed by Liang et al [25]. In CLPSO a particle not only learns from its own experience but also on the best experiences of all the particles which helps the swarm from premature convergence to a local minimum [26]. Although the algorithm performed well in multi modal problems, it did not provide good solutions for unimodal problems. Another variant of the PSO algorithm is the Dynamic Neighbourhood Learning Particle Swarm Optimizer (DNLPSO) proposed by Nasi et al. In this variant each particle learns from its experience and also from the experience of a dynamically changing neighbourhood. Learning from a dynamically changing neighbourhood helps in diversifying the learning experience of each particle and prevents premature convergence [27]. However, since the particles learn from the neighbourhood which is chosen at random, the particles might not be guided correctly. The DNLPSO algorithm is used for comparison in this paper.

• A.    Improving accuracy with local search

Stochastic algorithms like PSO are computationally expensive because they perform a random walk in the search space to explore multiple local minima and hence tend to converge slowly. On the other hand deterministic local search algorithms are computationally efficient but perform a local search [8]. Thus approaches that combine the advantages of global and local search algorithms are of interest [3]. The Nelder Mead Simplex method is a derivative free local optimization technique used to minimize or maximize an objective function in an unconstrained multidimensional space [28]. In the case of a bi-variable function, the simplex forms a triangle and the technique performs a pattern search which computes function values at every vertex. The vertex which has the largest value in the case of a minimizing problem will reinstated by a new vertex. A new triangle is formed and the search continues. The method results in a series of triangles, for which the values of the function at every vertex progressively reduces. The triangle size is then progressively decreased and the coordinates of the least points are determined. The NM-Simplex method is computationally efficient and robust [28, 29]. In this paper Nelder-Mead Simplex method is used to refine the solution found by the PSO for the ANN training problem.

• VI. A N ew Q uantum T unneling P article S warm O ptimization A lgorithm (Q tpso )

The global exploration ability of the classical PSO algorithm is limited because the personal best solution found by each particle always moves down the surface of the cost function towards smaller values resulting in a greedy search heuristic. Since the personal best solution always moves downhill it will always converge towards a nearby local minima. In this paper the personal best solution of each particle is allowed to tunnel through peaks in the cost function surface analogous to tunneling of quantum mechanical particles.

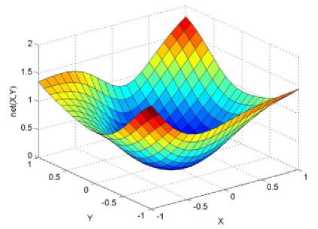
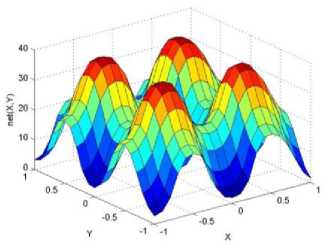
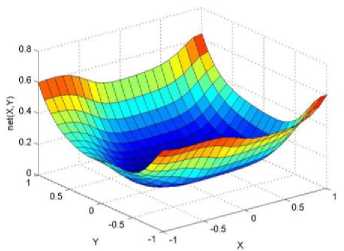
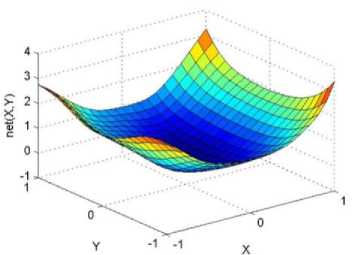
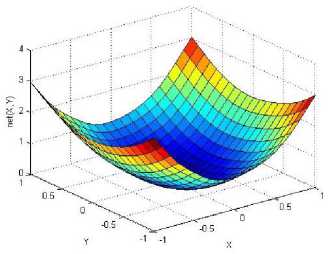
In classical mechanics a particle cannot cross a potential barrier if its total energy is less than that of the barrier. However, in quantum mechanics a particle without sufficient energy can still cross the potential barrier with a small probability. Fig. 2 depicts the quantum tunneling effect in QTPSO. The particle is allowed to tunnel through the peaks in the cost function surface. Thus the personal best solution can tunnel through peaks in the cost function to reach even lower values and avoid getting trapped in local minima. If the cost C(x) at the newly computed position x is less than C(x), the cost at the current position x , the new position is accepted with a probability 1. However, if C(x) is greater than C(x) the new position is not discarded but accepted with a probability that depends on the difference between the costs and distance between the two positions. Analogous to quantum tunneling it is proposed that the tunneling probability decrease with respect to barrier height and length. The probability of accepting the new position x is given in (5).

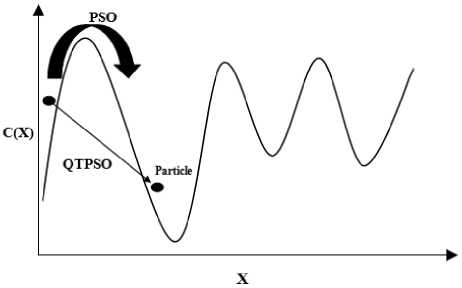
Fig.2 The quantum tunneling effect in QTPSO. The particle tunnels through the peaks in the cost function surface.

T he P roposed Q uantum T unneling P article S warm O ptimization A lgorithm (Q tpso )

Fori = 1 toN

Initialize x⁰⁾ in [x_mm_r x _mcT ]D randomly with uniform probability

Let i16'" = arg min, C(x')

LetE = E-„

For r = 1 tol^

Forp = 1 toN

-

Ap)

“Z^.v + ^x^, -х^сд^* -x®))

iv := maxfx" jw )

7 max /

r/o

AP)

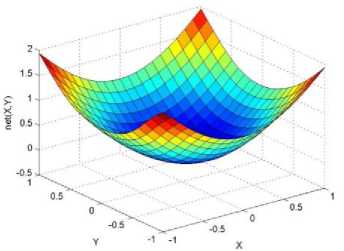
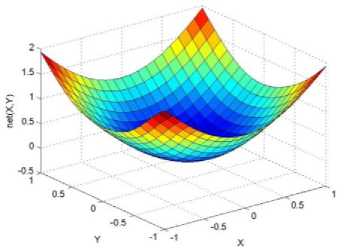
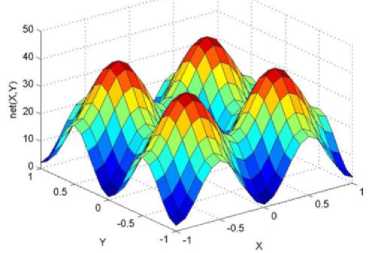
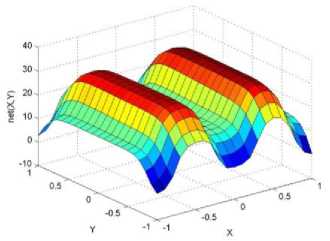
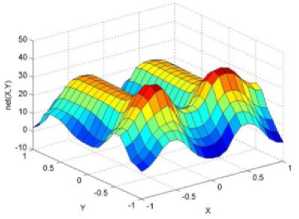
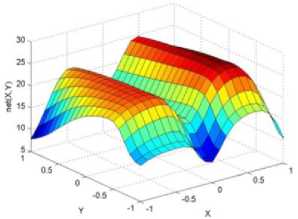
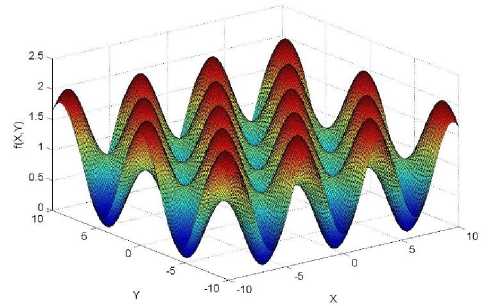
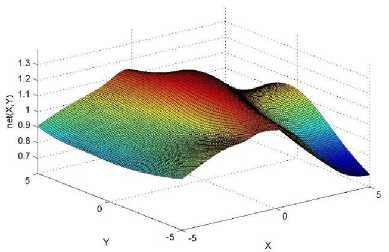
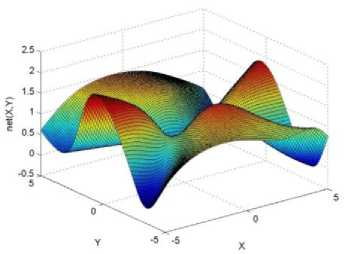
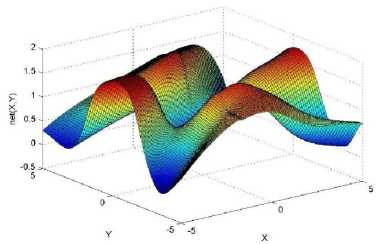
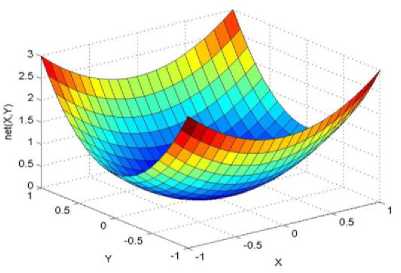
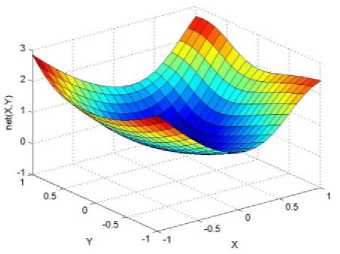
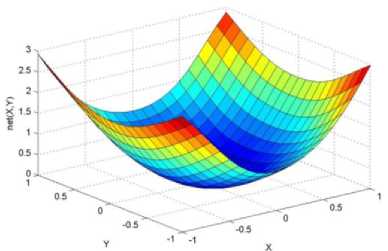
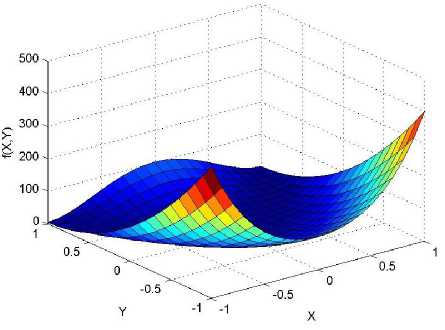
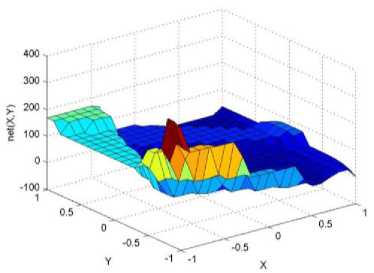
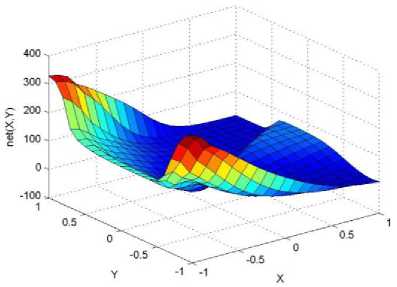
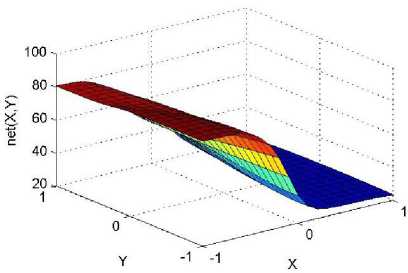
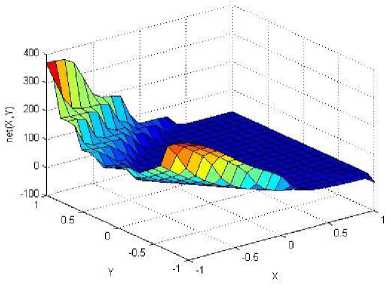
Ap) ._ _Y(p),,. _y

If C(^>)

' pbest " Else

Pt^-x^-e

Decrease E

E\=E ---

^ (l-^max)

Perform Nelder Mead Simplex with x° as the initial point and store the result in. Return x

If C (X⁽p)) < C (X^Ppbe_St )

^{P (X} ^ ^Xp ) = ¹

Else

• -((^C (Xp) - C (x ))||Xp - X

P⁽x ^ Xp) = e--------------⁽⁵⁾

E

Where P is the probability that the x will be accepted as the new position; x is the current position and x is the new position computed by PSO algorithm; C(x) is the cost function evaluated at x ; E is the Tunneling field.

Table 1. Nomenclature used in QTPSO

Symbol	Description
N	Size of the swarm
x(i)	Position of the ithparticle in the swarm
D	Dimension of the search space
vel(i)	Velocity of the ithparticle
pbest(i)	Personal best solution of the ithparticle
gbest	Global best solution

VII. Results and Discussion

The performance of the QTPSO algorithm was compared with three heuristic global optimization algorithms on benchmark feedforward neural network function approximation tasks. The architecture of the feedforward network consisted of two inputs, 10 hidden tansigmoidal hidden layer neurons and one linear output neuron. This feedforward network was trained to learn the 2D De Jong test suite of functions using different heuristic global optimization algorithms and the proposed

QTPSO algorithm. The De Jong test suite of benchmark functions that are used to compare the performance of the proposed QTPSO and the PSO variants are listed in Table 2. The De Jong test suite provides common challenges that the global optimization algorithms face, such as multiple local minima, flat regions and narrow ridge [5]. The performance of the QTPSO algorithm was compared with the classical PSO algorithm and hybrid PSO algorithms such as Nelder Mead Particle Swarm Optimization Algorithm (NMPSO), Dynamic Multi Swarm Particle Swarm Optimization Algorithm (DNLPSO). The mean square error obtained between the neural network’s output trained using the various algorithms and the ideal output was chosen as the performance metric in this paper.

Fig.3. Plot of the ideal Sphere Test Function

Fig.4. Approximation of sphere function learnt by an ANN trained with classical PSO algorithm.

Fig.5. Approximation of sphere function learnt by an ANN trained with NMPSO algorithm.

Table 2. De Jong’s test suite of functions

Function	Definition
Sphere	f(x, y) = x2 + y2
Rastrigin	f (x, y) = 20 + x2+ y2— 10(cos 2nx + cos 2ny)
Griewangk	fз(x,y) = (X4o+oy )  (COS(x)*cos(^)) +1
Ellipsoid	f,(x, y) = x2 + 2* y2
Rosenbrock	f5( x, y) = 100*(y - x2)2+ (x — 1)2

Fig.6. Approximation of sphere function learnt by an ANN trained with QTPSO algorithm.

Fig.7. Approximation of sphere function learnt by an ANN trained with classical DNLPSO algorithm.

• B.    BENCHMARK PROBLEM 2

f₂ (x, y) = 20 + x²+ y²-10(cos 2nx + cos 2ny)

Benchmark problem 2 considers approximating the Rastrigin function. Rastrigin function is highly multimodal and tests the ability of the global optimization algorithm to escape from local minima. A plot of the ideal Rastrigin function is in fig. 8. Fig. 9 indicates that the approximation of the Rastrigin function learnt by an ANN trained with the QTPSO algorithm is superior to the other algorithms.

Fig.8. Plot of the ideal Rastrigin Test Function

Fig.9. Approximation of rastrigin function learnt by an ANN trained with QTPSO algorithm

Fig.10. Approximation of rastrigin function learnt by an ANN trained with classical PSO algorithm

Fig.11. Approximation of rastrigin function learnt by an ANN trained with NMPSO algorithm

Fig.12. Approximation of rastrigin function learnt by an ANN trained with classical DNLPSO algorithm

• C.    BENCHMARK PROBLEM 3

f, (x, y) = ⁽x⁺y ) - (cos(x) * cos(-y)) + 1

3         4000                 2

Benchmark problem 3 considers the approximating the Griewangk function. The function is highly multimodal and tests the algorithm’s ability to explore the search space and escape local minima.

A plot of the ideal Griewangk test function is shown in fig. 13. The approximation of the Griewangk test function learnt by the neural networks trained with different global optimization algorithms is in figs.14 to 17. Fig. 16 indicates that the approximation of the Griewangk function learnt by an ANN trained with the QTPSO algorithm is superior to the approximation learnt with PSO, NMPSO and DLNPSO algorithms.

Fig.13. Plot of the ideal Griewangk Test Function

Fig.14. Approximation of Griewangk function learnt by an ANN trained with classical PSO algorithm

Fig.15. Approximation of Griewangk function learnt by an ANN trained with NMPSO algorithm

Fig.16. Approximation of Griewangk function learnt by an ANN trained with QTPSO algorithm

Fig.17. Approximation of Griewangk function learnt by an ANN trained with DNLPSO algorithm

• D.    BENCHMARK PROBLEM 4

f₍(x, y) = x²+ 2* y²

Benchmark problem 4 considers approximating the Ellipsoid function. The function is continuous and unimodal. A plot of the ideal Ellipsoid function is shown in fig. 18. The approximation of the Ellipsoid test function learnt by the neural networks trained with different global optimization algorithms is in figs. 19 to 22. Fig. 22 indicates that the approximation of the Ellipsoid function learnt by an ANN trained with the QTPSO algorithm is superior to the approximation learnt with PSO, NMPSO and DLNPSO algorithms.

Fig.18. Plot of the ideal Ellipsoid Test Function

Fig.19. Approximation of Ellipsoid function learnt by an ANN trained with classical PSO algorithm

Fig.20. Approximation of Ellipsoid function learnt by an ANN trained with NMPSO algorithm

Fig.21. Approximation of Ellipsoid function learnt by an ANN trained with DNLPSO algorithm

Fig.22. Approximation of Ellipsoid function learnt by an ANN trained with QTPSO algorithm

• E.    BENCHMARK PROBLEM 5

f_;(x, y) = 100*(y - x 2)2 + (x-1)2

Benchmark problem 5 considers the approximating the Rosenbrock’s function. Rosenbrock function has a very narrow ridge. Algorithms that are not able to discover good directions underperform in this problem. An ideal plot of the function is shown in Fig. 23. The approximation of the Rosenbrock’s test function learnt by the neural networks trained with different global optimization algorithms is in figs. 24 to 27. Fig. 27 indicates that the approximation of the Rosenbrock’s function learnt by an ANN trained with the QTPSO algorithm is superior to the approximation learnt with PSO, NMPSO and DLNPSO algorithms.

Fig.23. Plot of the ideal Rosenbrock’s Test Function

Fig.24. Approximation of Rosenbrock’s function learnt by an ANN trained with classical PSO algorithm

Fig.25. Approximation of Rosenbrock’s function learnt by an ANN trained with NMPSO algorithm

Fig.26. Approximation of Rosenbrock’s function learnt by an ANN trained with DNLPSO algorithm

Fig.27. Approximation of Rosenbrock’s function learnt by an ANN trained with QTPSO algorithm

Table 3 presents the mean square function approximation error for a feedforward ANN trained with different PSO variants. Table 3 clearly indicates that the QTPSO algorithm proposed in this paper significantly outperforms the classical PSO and state-of-the-art PSO algorithm variants on benchmark ANN training problems.

Table 3. Comparison of Mean Square Function Approximation Errors

Test Function	PSO	NMPSO	DNLPSO	QTSPO
Sphere	0.006	0.001	0.0035	1.68e-04
Rastrigin	0.094	0.005	34.5732	9.89e-04
Griewangk	0.237	0.055	9.25e-04	2.29e-04
Ellipsoid	0.016	0.001	0.0090	1.70e-03
Rosenbrock	1.4e+03	967.6	4.11e+03	468.24

• VIII. Conclusion

In this paper a new quantum tunneling PSO algorithm was proposed and applied to the problem of training feedforward neural networks to learn the challenging De Jong’s suite of benchmark functions. The problem of the personal best solution in the PSO algorithm getting trapped in local minima is overcome by allowing the personal best solution to tunnel through peaks in the cost function analogous to the tunneling phenomenon in Quantum Mechanics. In this paper the final solution is also refined with local search to avoid wasting computational effort performing stochastic search once the global minimum is approximately located. Thus inclusion of the quantum tunneling effect allows many local minima to be explored and local search allows each local minimum to be accurately calculated. Simulation results on benchmark feedforward ANN function approximation problems indicate that the QTPSO algorithm proposed in this paper outperforms the three state-of-the-art heuristic global optimization algorithms. Future work can explore the effect of allowing the individual particles to also tunnel or take random jumps according to different probability distributions to further improve the explorative ability of the QTPSO algorithm. The use of low cost GPU hardware to reduce execution time of different PSO algorithms can also be explored.