A Note on Determinant and Adjoint of Fuzzy Square Matrix

Published Online April 2013 in MECS

• I.    Introduction

  Matrices with entries in [0, 1] and matrix operation defined by fuzzy logical operations are called fuzzy matrices. All fuzzy matrices are matrices but every matrix is not a fuzzy matrix. Fuzzy matrices play a fundamental role in fuzzy set theory. They provide us with a rich framework within which many problems of practical applications of the theory can be formulated. Fuzzy matrices can be successfully used when fuzzy uncertainty occurs in a problem. These results are extensively used for cluster analysis and classification problem of static patterns under subjective measure of similarity. On the other hand, fuzzy matrices are generalized Boolean matrices which have been studied for fruitful results. And the theory of Boolean matrices can be back to the theory of matrices with non negative contents, for which most famous classical results were obtained 1907 to 1912 by Parren and Frobenius. So the theory of fuzzy matrices is interesting in its own right. An important connection between fuzzy sets and fuzzy matrices has been recognized and this has led us to define fuzzy matrices in a quite different way.

Fuzzy matrix has been proposed to represent fuzzy relation in a system based on fuzzy set theory [1]. Fuzzy matrices were introduced first time by Thomson [2], who discussed the convergence of powers of fuzzy matrices. Several authors had presented a number of results on the covergence of power sequences of fuzzy matrices. Several authors have presented a number of results on the convergence of power sequence of fuzzy matrices [3, 4, 5]. Fuzzy matrices play an important role inscience and technology. Kim [6,7] represented some important result on the determinant of a square matrix. He defined the determinant of a square fuzzy matrix and contributed with very research works [6, 7,8, 9] a lot to the study of determinant theory of square fuzzy matrices. The adjoint of square fuzzy matrix was defined by Thomson [2] and Kim[6].

The properties of a square fuzzy matrix are somewhere analogus to the crisp case for determinant of a square fuzzy matrix and also for adjoint of square fuzzy matrices. Since for finding determinant and adjoint of square fuzzy matrices first thing we need is the definition of square fuzzy matrix. Let us have a look at it.

Square Fuzzy Matrices

A fuzzy matrix is a matrix which has its elements from the interval [0, 1], called the unit fuzzy interval. A m x n fuzzy matrix for which m=n (i.e the number of rows is equal to the number of columns) and whose elements belong to the unit interval [0, 1] is called a fuzzy square matrix of order n.

A fuzzy square matrix of order two is expressed in the following way

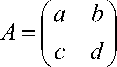
where the entries a,b,c,d all belongs to the interval [0,1].

In accordance with the process of defining complementation of a fuzzy set as defined by Baruah [10,11, 12], a fuzzy set

A = {x, ^(x), x G X} would be defined in this way as

A = {x, д(x), 0, x g X} so that the complement would become

A^c = { x , 1, д ( x ), x e X }

A = [ a„U

Thus a square fuzzy matrix       j nxn would be represented according to the new definition as

A = [( a . ,0)]

' ^j     n ^x n and similarly the complement matrix

A^c = [(1, a . )]

of the matrix A would be       1  ’ j ]nnxn . The following example will make it clear.

The matrix A would be defined according to our way as

' ( a ,0)   ( b ,0)"

_v ( c ,0)  ( d ,0) ,

Because we are interested in defining fuzzy sets with the help of reference function.

Similarly the complement of the matrix A would take the form

• II.    Determinant of a Square Fuzzy Matrix

The determinant of the fuzzy matrix A would be denoted by

( a ,0)  ( b ,0)

( c ,0)  ( d ,0)

and we would like to expand the above determinant in the following way

I A =

( a ,0)  ( b ,0)

( c ,0)  ( d ,0)

=[max{min(a,d),min(b,c)}, min{max(0,0),max(0,0)}]

Now for the a square fuzzy matrix of order 3

' ( a . ,0)

B = ( a ₂,0)

( b 1 ,0)

( b 2 ,0)

( c 1 ,0)

( c 2 ,0)

' (1, a )   (1, b )"

. (1, c )   (1, d ) ,

( ( a 3 ,0)  ( b „0)  ( c 3 ,0)

The determinant would be denoted by

It is important to mention here the fact that for finding the adjoint of a square fuzzy matrix, we need the help of determinant of the matrix. It is for this reason; we would like to show the way in which the determinant of a square fuzzy matrix should be expanded in order to keep pace with the representation of fuzzy matrices in terms of reference function. It is seen the representation of fuzzy sets with the help of reference function is very essential in getting logical result which in turn has led the foundation of representing fuzzy matrices with the help of reference function. In the next section, we shall deal with the determinant theory of square fuzzy matrices and some of its properties.

Before proceeding further, let us define two operations which are mostly required in case of finding the determinant of fuzzy matrices

( a ,b) + (c, d)={max(a,c),min(b,d)}

(a,b) (c ,d)= {min (a, c), max (b, d)}

The paper is organized as follows: Section II describes the definition of determinant ofsquare fuzzy matrices which is followed by some numerical examples along with the properties of square fuzzy matrices which are discussed in the subsections considered. Section III introduces the new definition of adjoint of square fuzzy matrices which is again followed by some numerical examples and the various properties of square fuzzy matrices are discussed in the subsections of this section. Finally, Section VI presents our conclusions.

(a1,0) (b1,0) (c1, 0) (a2,0) (b2,0) (c2,0) (a3,0) (b3,0) (c3,0) and this would be defined as

= ( a 1 ,0)

( b 2 ,0)

( b 3 ,0)

( c 2 ,0)          ( a 2 ,0)  ( c 2 ,0)

+ ( b , 0)

( c 3 ,0)      ¹      ( a 3 ,0)   ( c 3 ,0)

( a 2 ,0)  ( b 2 ,0)

( a 3 ,0)  ( b 3 ,0)

= (a1,0) [max{min( b2 , c3 )  , min( b3 , c2 )}, min{max(0,0), max(0,0)} + ( 1, ) [max{min( a2 , c3 )

min( a ³ , c ² )}, min{max(0,0), max(0,0)}+ ( c ¹ , ) [max{min( a ² , ³ ) min( a ³ , ² )}, min{max(0,0), max(0,0)}.

It would be easy to proceed with the usual fuzzy matrices whose reference functions are taken as zero and it is due to this reason we would like to focus on the complementation of fuzzy matrices.

Taking into consideration of the above mentioned procedure for representing fuzzy matrices along with the definition of complementation of fuzzy sets, the complement of the above fuzzy matrix B can be written as

( (1, a j   (1, a 2 )   (1, a 3 ) ^

(1, b i )   (1, b 2 )   (1, Ь з )

( (1, C 1 )   (1, c 2 )   (1, C 3 ) J

Then the determinat of the above complement matrix would be evaluated as

(1, b 2 )   (1, c 2 )           (1, a 2 )   (1, c 2 )

(1, b 3 )   (1, c 3 )   ^{(, 1 )}(1, a 3 )   (1, c 3 )

(1, a 2 )   (1, b 2 )

(1, a 3 )   (1, b 3 )

= ( , a ¹ ) [max{min(1,1),min(1,1)},min{max( ² , c ³ ), max( ³ , c ² )}] + ( , ¹ ) [max{min(1,1),min(1,1)}, min{max ( a ² , c ³ ), max ( a ³ , c ² )}+ (1 c ) a b

, ¹ [max{min(1,1), min(1,1)}, min{max( ² , ³ ), max( a ³ , ² )}

It is to be noted here that the above determinant is expanded along the first row. But it can be easily observed that the value of the determinant remains unchanged if it is expanded along any row or columns.

• 2.1    Numerical Examples

Here we shall put a numerical example to find the determinant of a fuzzy matrix in the way described above.

Ac

^z (1,0.5)  (1,0.3)  (1,0.8)'

(1,0.6)  (1,0.2)  (1,0.9)

_v (1,0)   (1,0.7)  (1,0.4) j

Then the determinant of the above matrix when expanded along the first row would give us the following result

I A^c\ = (1,0.5)

(1,0.2)

(1,0.9)

(1,0.7)

(1,0.4)

+ (1,0.6)

(1,0.3)

(1,0.8)

(1,0.7)

(1,0.4)

(1,0.3)  (1,0.2)

(1,0.8)  (1,0.9)

= (1,0.5)[max(1,1), min(0.4,0.9)] + (1,0.3) [max(1,1), min(0.6,1)] + (1,0.8)[max(1,1), min(0.2,0.7)]

=(1,0.5) (1,0.4)+ (1,0.3) (1,0.6)+ (1,0.8) (1,0.2)

=[max{min(1,1)},min{max(0.5,0.4)}]+ max{min(1,1)}, min{max(0.3,0.6)}] + [max{min(1,1)}, min{max(0.8, 0.2)}]

= (1, 0.5) + (1, 0.6) + (1, 0.8)

= {max (1, 1), min (0.5, 0.6)} + (1, 0.8)

= (1, 0.5) + (1, 0.8)

= {max (1, 1), min (0.5, 0.8)}

= (1, 0.5)

• 2.2    Some Properties of Determinant of Square Fuzzy Matrix

• 2.2.1    Property1

This section would deal with some of the properties of the determinant of square fuzzy matrices when the reference function is taken into consideration for representing fuzzy matrices.

The value of the determinant remains unchanged when any two rows or columns are interchanged.

Let us consider the determinant of the above matrix with 1st and 2nd columns interchanged.

	(1,0.3) (1,0.2) (1,0.7)		(1,0.5) (1,0.6) (1,0)	(1,0.8) (1,0.9) (1,0.4)
	(1,0.3)	(1,0.6)		(1,0.9)
			(1,0)	(1,0.4)
+ (1,0.5)			(1,0.2)	(1,0.9)
			(1,0.7)	(1,0.4)
+ (1,0.8)			(1,0.2)	(1,0.6)
			(1,0.7)	(1,0)

=(1,0.3) [max(1,1), min(0.6, 0.9)] + (1,0.5) [max(1,1), min(0.4, 0.9)] + (1,0.8) [max(1,1), min(0.2, 0.7)]

=(1,0.3) (1,0.6) + (1,0.5) (1,0.4)+(1,0.8) (1,0.2)

=[max{min(1,1)}, min{max(0.3,    0.6)}]    +

[max{min(1,1)},     min{max(0.5,     0.4)}]     +

[max{min(1,1)}, min{max(0.8, 0.2)}]

=(1,0.6)+(1,0.5)+(1,0.8)

= {max (1, 1), min (0.6, 0.5)} + (1, 0.8)

= (1, 0.5) + (1, 0.8)

= {max (1, 1), min (0.5, 0.8)

= (1, 0.5)

Thus the values of the determinant remain unchanged if the rows and columns are interchanged.

• 2.2.2    Propery2

The values of the determinant of fuzzy square matrix remain unchanged when rows and columns are interchanged.

Let us consider the following matrix which is obtained by interchanging the rows and columns of the above matrix A^c

Г (1, a 1 )   (1, a 2 )   (1, a 3 ) ^

(1, b_x)   (1, b 2 )   (1, Ь з )

( (1, c 1 )   (1, c 2 )   (1, c 3 ) J

(1, b 2 )   (1, b 3 )           (1, a 2 )   (1, a 3 )

(1, c 2 )   (1, c 3 )   ^{(, 1 )}(1, c 2 )   (1, c 3 )

= (1,0.5)	(1,0.2)	(1,0.7)
	(1,0.9)	(1,0.4)
+ (1,0.6)	(1,0.3)	(1,0.7)
	(1,0.8)	(1,0.4)

(1,0.3)  (1,0.2)

(1,0.8)  (1,0.9)

=(1,0.5)[max(1,1), min(0.4,0.9)] + (1,0.6)[max(1,1), min(0.4,0.8)]+(1,0.8)[max(1,1), min(0.9, 0.8)]

=(1,0.5)(1,0.4)+(1,0.6)(1,0.4)+(1,0.8)(1,0.8)

=(1,0.5)+(1,0.6)+(1,0.8)

= (1, 0.5) + (1, 0.8)

= (1, 0.5)

• 2.2.3    Property3

If Ac and Bc be two square fuzzy matrices then the following property will hold det( AcBc) * det Ac det Bc

Bc

Г (1,0.3)    (1,1)    (1,0.7) "

(1,1)    (1,0.9)    (1,0)

, (1,0.8)  (1,0.2)  (1,0.3) j

+ (1, C 1 )

(1, a 2 )

(1, b 2 )

(1, a 3 )

(1, b 3 )

Proceeding in the similar manner we would get the value of the determinant of B^c as (1, 0.9).

Hence we get

Then the determinant of the above complement matrix would be evaluated as det(ACB) = (1,0.5)(1,0.9)

(1, b 2 )   (1, b 3 )           (1, a 2 )   (1, a 3 )

(1, c 2 )   (1, c 3 ) + ^{(, 1 )}(1, c 2 )   (1, c 3 )

= (1, 0.9)

det( A^cB^c )

Now in order to find we would have to

+ (1, c j

(1, a 2 )

(1, b 2 )

(1, a 3 )

(1, b 3 )

see whether the product of the two fuzzy matrices A^c and B^c is defined. So we should first define the multiplication of two fuzzy matrices when represented with the help of reference function.

Numerical Example

With the help of this numerical example, it is expected that the property which is stated to hold true would be clear

Let us consider thefollowing determinant

(1,0.5)  (1,0.6)   (1,0)

(1, 0.3) (1,0.2)  (1, 0.7)

(1,0.8) (1,0.9)  (1,0.4)

Before proceeding further let us define the multiplication of two fuzzy matrices for illustration purposes.

• 2.2.4    Multiplication of Two Square Fuzzy Matrices

Now after finding addition of fuzzy matrices, we shall try to find the multiplication of two fuzzy matrices .The product of two fuzzy matrices under usual matrix multiplication is not a fuzzy matrix. It is due to this reason; a conformable operation analogus to the product which again happens to be a fuzzy matrix was introduced by many researchers which can be found in fuzzy literature which can be found in the reference [1]. However, even for this operation the product AB to be defined if the number of columns of the first fuzzy matrix A is equal to the number of rows of the second fuzzy matrix B. In the process of finding multiplication of fuzzy matrices, if this condition is satisfied then the multiplication of two fuzzy matrices A and B, will be defined and can be represented in the following form:

AB = {max min( a^ , b _t ), min max( r^ , r ‘ ) }

square fuzzy matrix of order (n-1) obtained from a square fuzzy matrix A of order n by deleting row and column i. Then the matrix B is defined as the adjoint of the matrix A. It is to be noted here that the adjoint of a matrix is of the same order as that of the given matrix.

Here in this article, we would like to represent a

fuzzy matrix        ij in the form after considering reference function to serve our purpose. Then the

adjoint will take the form

B = [( b j ,0)]

The

Where

A = ^K a j , r )]  a nd   ^B = [( b j , r i ' )]

1 < i < n , 1 < j < n and j , stands for the membership function of the fuzzy matrix A and the

r corresponding reference function is ij whereas b ij stands for the membership function of the fuzzy

r matrix B with the corresponding reference function ji .

membership value matrix which can be obtained from this representation would coincide with that of usual matrix representation. But before proceeding further let us have a look at the way in which the adjoint of fuzzy matrices are to be defined in our way.

Now if we consider two fuzzy square matrices Ac and Bc as described previously then we have the product AcBc as ' (1,0.5)  (1,0.3)  (1,0.8) ^ ' (1,0.3)    (1,1)    (1,0.7)" (1,0.6)  (1,0.2)  (1,0.9) (1,1)    (1,0.9)   (1,0) , (1,0)   (1,0.7)  (1,0.4), v (1,0.8)  (1,0.2)  (1.0.3) ? Which when calculated with our method of multiplication would give us the following result

A c | = (1,0.5)	(1,0.2)	(1,0.7)
	(1,0.9)	(1,0.4)
+ (1,0.6)	(1,0.3)	(1,0.7)
	(1,0.8)	(1,0.4)
+ (1,0)	(1,0.3)	(1,0.2)
	(1,0.8)	(1,0.9)

^b 11 = I ^A 111 =

( b 2 ,0)

( b 3 ,0)

( c 2 ,0)

( c 3 ,0)

=[max{min( ² , c ³ ),min( ³ , c ² )},min{max(0,0),max (0,0)}]

^z (1,0.5)  (1,0.8)  (1,0.3)'

(1,0.6)  (1,0.9)  (1,0.2)

_v (1,0.3)  (1,0.4)  (1.0.4) ,

^b 12   I A 21I

( a ₂,0) ( a ,0)

( c 2 ,0)

( c 3 ,0)

=[max{min( a ² , c ³ ),min( a ³ , c ² )},min{max(0,0),ma x(0,0)}]

Now the determinant of the above fuzzy square matrix is (1, 0.5) which states the fact that det(AcBc) * det Ac det Bc

^b 13    | ^A 31|

( a 2 ,0)

( a 3 ,0)

( b 2 ,0)

( b 3 ,0)

In the above section, we have gone through the new method of defining the determinant of square fuzzy matrices and thereafter some properties of the determinant are studied. The next section is contributed to deal with the adjoint theory of square fuzzy matrices.

=[max{min( a ² , ³ ),min( a ³ , ² )},min{max(0,0),ma

x(0,0)}]

Similarly we are to find the others.

Then the adjoint of the matrix B would symbolically be represented as

III. Adjoint of Square Fuzzy Matrix

Let A = ^[ a j ^]   be any matrix. Then B = ^[ b j ^] n ^x n

.   bj =1 Al KI . „ where           and       is the determinant of the

' ( b 11 ,0) adjB = ( b _{2 n}0)

. ( b 31 ,0)

( b 12 ,0)   ( b 13 ,0)^л

( b 22 ,0)  ( b 23 ,0)

( b 32 ,0)  ( Ь зз ,0) _V

3.1 Numerical Example

To illustrate the introduced concept we want to cite the following numerical example. Let us consider a square fuzzy matrix of order 3 as

Ac

^ (1,0.5)  (1,0.3)  (1,0.8)'

(1,0.6)  (1,0.2)  (1,0.9)

_v (1,0)   (1,0.7)  (1,0.4) ,

Then we have

(1,0.2)  (1,0.9)

=

¹¹    (1,0.7)  (1,0.4)

= [max {min (1, 1), min (1, 1)

min {max(0.2, 0.4), max(0.7,0.9)}]

= [max (1, 1), min (0.4, 0.9)]

= (1, 0.4)

(1,0.6)  (1, 0.9)

(1,0)   (1,0.4)

= [max {min (1, 1), min (1, 1)

min {max(0.6, 0.4), max(0,0.9)}]

= [max (1, 1), min (0.6, 0.9)]

= (1, 0.6)

(1,0.6)  (1,0.2)

(1,0)   (1, 0.7)

= [max {min (1, 1), min (1, 1)

min {max(0.6, 0.7), max(0,0.2)}]

= [max (1, 1), min (0.7, 0.2)]

= (1, 0.2)

Similarly b21 = (1,0.4), b22 = (1,0.5), b . = (1,0.3)

b ₃₁ = (1,0.8), b ₃₂ = (1,0.8), b ₃₃ = (1,0.5)

Hence the adjont of the matrix A^c will become

' (1,0.4)

adjA = (1,0.4)

. (1,0.8)

(1,0.6)  (1,0.2) "

(1,0.5)  (1,0.3)

(1,0.8)  (1,0.5) _v

• 3.2 Property

• 3.2.1    Property1

If A^c be a fuzzy square matrix, then we get

Ac (adjAc) * (adjA) Ac

Now let us find the following

Ac(adjAc)

' (1,0.5)  (1,0.3)  (1,0.8) '

=   (1,0.6)  (1,0.2)  (1,0.9)

₄ (1,0)   (1,0.7)  (1,0.4) ,

' (1,0.4)  (1,0.6)  (1,0.2) ^

(1,0.4)  (1,0.5)  (1,0.3)

. (1,0.8)  (1,0.8)  (1,0.5) ,

A c ( adjA c ) = [ C j J (say)

Where

= [max {min (1, 1), min (1, 1), min (1, 1)}, min {max(0.5,0.6), max(0.3,0.2), max(0.8,0.4)}]

= {max (1, 1, and 1), min (0.6, 0.3, and 0.8)}

= (1, 0.3)

= [max {min (1, 1), min (1, 1), min (1, 1)}, min {max(0.5,0.4), max(0.3,0.5), max(0.8,0.3)}]

= {max (1, 1, and 1), min (0.5, 0.5, and 0.8)}

= (1, 0.5)

= [max {min (1, 1), min (1, 1), min (1, 1)}, min {max(0.5,0.8), max(0.3,0.8), max(0.8,0.5)}]

= {max (1, 1, and 1), min (0.8, 0.8, and 0.8)}

= (1, 0.8)

Similar calculation would give us the following results

C 21 = (1,0.2), C 22 = (1,0.5), C 23 = (1,0.8)

C 31 = (1,0.4), C 32 = (1,0.4), C 33 = (1,0.5)

Thus we see that

	(1,0.4)  (1,0.5)  (1,0.3)	Hence the following result is obtained
AadjA =	(1,0.4)  (1,0.5)  (1,0.3)	det ( adjAc ) = det Ac
	(1,0.4)  (1,0.6)  (1,0.2) v
Similarly we get		3.2.3 Property3
C31 = (1,0.4), C 32 = (1,0.4), C 33 = (1, 0.5)               If A be a fuzzy square matrix, we shall show that
	' (1,0.2)  (1,0.4)  (1,0.4)'	det A ( adj A ) = det Ac = det( adj A ) Ac
( adj A ) A =	(1,0.3)  (1,0.4)  (1,0.4)	Here
	v (1,0.5)  (1,0.7) (1,0.5)	det Ac ( adj A )

So here it is observed that in case of fuzzy square matrices

Ac (adj A) * (adj A) Ac

• 3.2.2    Property2

If Ac be a fuzzy square matrix, then det (adjAc) = det Ac

We have already found the adjoint of the fuzzy matrix adjA and so we would like to calculate the determinant of this matrix

adjA\ = (1,0.4)	(1,0.5)	(1,0.3)
	(1,0.8)	(1,0.5)
+ (1,0.6)	(1,0.4)	(1,0.3)
	(1,0.8)	(1,0.5)
+ (1,0.2)	(1,0.4)	(1,0.5)
	(1,0.8)	(1,0.8)

=(1,0.4)[max{min(1,1),min(1,1)}, min{max(0.5, 0.5),max(0.3,0.8)}]

+(1,0.6)[max{min(1,1),min(1,1)}, min{max(0.4,0.5),max(0.8, 0.3)}]

+(1,0.2)[max{min(1,1),min (1, 1)}, min{max (0.4, 0.8), max (0.5, 0.8)}]

=(1,0.4)(1,0.5)+(1,0.6)(1,0.5)+(1,0.2)(1,0.8)

=(1,0.5)+(1,0.6)+(1,0.8)

= (1, 0.5) + (1, 0.8)

= (1, 0.5)

Similarly, we get detAc=(1,0.5)

= (1,0.4)	(1,0.5) (1,0.6)	(1,0.3) (1,0.2)
+ (1,0.5)	(1,0.4)	(1,0.3)
	(1,0.4)	(1,0.2)
+ (1,0.3)	(1,0.4)	(1,0.5)
	(1,0.4)	(1,0.6)

=(1,0.4)[max{min(1,1),min(1,1)}, min{max(0.5, 0.2),max(0.3,0.6)}]

+(1,0.5) [max{min(1,1),min(1,1)}, min{max(0.4,0.2),max(0.4, 0.3)}]

+(1,0.3)[max{min(1,1),min (1, 1)}, min{max (0.4, 0.6), max (0.5, 0.4)}] =(1,0.4)(1,0.5)+(1,0.5)(1,0.4)+(1,0.3)(1,0.5) =(1,0.5)+(1,0.5)+(1,0.5)

= (1, 0.5) + (1, 0.5)

= (1, 0.5)

det(adjAc)Ac

= (1,0.2)	(1,0.4) (1,0.7)	(1,0.4) (1,0.5)
+ (1,0.4)	(1,0.3)	(1,0.4)
	(1,0.5)	(1,0.5)
+ (1,0.4)	(1,0.3)	(1,0.4)
	(1,0.5)	(1,0.7)

=(1,0.2)[max{min(1,1),min(1,1)}, min{max(0.4, 0.5), max(0.4,0.7)}]

+(1,0.4) [max{min(1,1),min(1,1)}, min{max(0.3,0.5), max(0.4, 0.5)}]

+(1,0.4)[max{min(1,1), min (1, 1)}, min{max (0.3, 0.7), max (0.4, 0.5)}]

=(1,0.2)(1,0.5)+(1,0.5)(1,0.4)+(1,0.3)(1,0.5)

=(1,0.5)+(1,0.5)+(1,0.5)

= (1, 0.5) + (1, 0.5)

= (1, 0.5)

det A^c =(1,0.5)

Thus we arrive at the result

• 3.2.4    Property4

If A^c and B^c be fuzzy square matrices then adj ( A^cB^c ) = adjA^cadjB^c

Let us consider the fuzzy square matrix B^c such that it is conformable for multiplication with previously cited fuzzy matrix A^c .

Let

	Bc =	^ (1,0.3) (1,0.1) v (1,0.8)	(1,1) (1,0.9) (1,0.2)	(1,0.7) "  (1,0) (1,0.3) ,
Let us calculate the product
AcBc
	' (1,0.5)	(1,0.3)	(1,0.8) л
=	(1,0.6)	(1,0.2)	(1,0.9)
	. (1,0)	(1,0.7)	(1,0.4) ,
	' (1,0.3)	(1,1)	(1,0.7) "
	(1,1)	(1,0.9)	(1,0)
	. (1,0.8)	(1,0.2)	(1,0.3) v
	' (1,0.5)	(1, 0.8)	(1,0.3)
=	(1,0.6)	(1,0.9)	(1,0.2)
	4 (1,0.3)	(1,0.4)	(1,0.4))
		' (1,0.4)	(1,0.3)	(1,0.6) "
adj ( AB ) =		(1,0.4)	(1,0.3)	(1,0.5)
		. (1,0.8)	(1,0.5)	(1,0.8) ,

Then proceeding in the same manner we get

' (1,0.2)

adjB = (1,0.8)

. (1,0.9)

(1,0.7) (1,0.3) (1, 0.2)

(1,0.9)

(1,0.3)

(1,0.9)

Thus we get

adjAcadjBc

' (1,0.4)  (1,0.6)  (1,0.2)

=   (1,0.4)  (1,0.5)  (1,0.3)

v (1,0.8)  (1,0.8)  (1,0.5)

л (1,0.2)  (1,0.8)  (1,0.9)

(1,0.7)  (1,0.3)  (1,0.2)

v (1,0.9)  (1,0.3) (1,0.9)

" (1,0.4)  (1,0.3)  (1,0.6)

=   (1,0.4)  (1,0.3)  (1,0.5)

v (1,0.8) (1,0.5)  (1,0.8)

Hence the result adj (AcBc) = adj A adjB is verified.

• 3.2.5    Property5

If A^c be fuzzy square matrices then

( adjA^c ) ‘ = adj ( A^c' )

Proof:

adj A = [(1, bj )]

Then

( adjA c ) ‘ = [(1, b j )]

Again adj A ’ = [(1, bj)]

In this way, we can claim that

( adj A ) ‘ = adj ( A^c' )

To make the matter clear and simple, we have put forward an example in support of the claim.

Numerical Example:

We have adjAc

' (1,0.4)  (1,0.6)  (1,0.2) "

(1,0.4)  (1,0.5)  (1,0.3)

_v (1,0.8)  (1,0.8)  (1,0.5) _v

And so

' (1,0.4)(adjAc)' = (1,0.6)

v (1,0.2)

(1.0.4)  (1,0.8)'

(1,0.5)  (1,0.8)

(1,0.3) (1,0.5) ,

Again	' (1,0.5)	(1,0.6)	(1,0) "
( A c ) ‘ =	(1,0.3)	(1,0.2)	(1,0.7)
	4 (1,0.8)	(1,0.9)	(1,0.4) ,

And

( (1,0.4)  (1,0.4)

(adjAc )‘= (1,0.6)  (1,0.5)

(1,0.8) "

(1,0.8)

(1,0.5),

( (1,0.2)  (1,0.3)

Hence we get

adj ( Ac )‘ = ( adj A)

These are some of the properties which are found to hold for the determinant of square fuzzy matrices represented with the help of reference function.

• IV. Conclusions

In this article, our main intention was to represent fuzzy matrices according to reference function and then to define the determinant and adjoint of square fuzzy matrices accordingly. We think that the representation of fuzzy sets with the help of reference function is very essential to have logical frameworks. Again while defining the determinant and adjoint of square fuzzy matrices with the help of reference function, some of the properties of the determinant as well as the adjoint of square fuzzy matrices were studied. In the process, it is found that the properties of the determinat and adjoint of square fuzzy matrices are somewhere analogus with the crisp cases.