A Note on Group Authentication Schemes

Published Online May 2016 in MECS

In order to ensure secure communication, before communicating the main protocol messages, a key establishment protocol will distribute session keys to all participants. This needs to provide confidentiality and authentication for the session keys. Confidentiality ensures the sender that the message can be read only by an intended receiver and authentication ensures the receiver that the message is sent by a specified sender and the message is not altered by another party.

There are different definition for authentication in literature. Gollmann [1] has put forward a number of different options for what could be meant by authentication.

Syverson and van Oorschot [2], identify what they term six `Generic Formal Goals'. They stated that, it is not intended as a 'definitive list of the goals that a key agreement or key distribution protocol should meet'.

Menezes et al . [3] give a more comprehensive definition as follows: “Entity authentication is the process whereby one party is assured (through acquisition of corroborative evidence) of the identity of a second party involved in a protocol, and that the second has actually participated (i.e., is active at, or immediately prior to, the time the evidence is acquired).”

In 1997 [4], Lowe suggested that the appropriate authentication requirement will depend upon the use to which the protocol is put, and proposed an

“authentication hierarchy”.

In this paper, we aim to discuss group authentication in conference (group) key establishment protocols involving more than two party, where a group key is needed to be shared for all group members. Group key establishment protocols fall in to two main categories: Key transfer protocols and Key agreement protocols [5].

Most group key agreement protocols are generalization of the Diffie-Hellman [6] key agreement protocol, such as, Ingemarsson et al . [7], Steer et al . [8], Burmester and Desmedt [9], and Steiner et al . [10]. In

• 1996,    Steiner et al . [10], proposed an extension of DH and in 2001, an authenticated version of it was proposed and has proved to be secure [11]. In 2007, Bresson et al . [12] constructed a generic authenticated group DH Key exchange. Also, in 2007, Katz and Yung [13] proposed the first constant-round and fully scalable group DH protocol.

The generalization of what authentication is in a group key agreement protocol is different from two party protocols. The potential problem is that in a two-party protocol, authentication means that the intended communication partner are assured about each other identity. But in a group it may be quite difficult to know who the communication partners in the group are.

Saeednia and Safavi-Naini [14] suggest that for a key establishment protocol every principal should be sure that either the same key is shared with all other principals or that no two principals share the same key. In particular they consider that a situation in which a session key is established by a subset of the intended set of principles, but is not known to other members of the set, which is a major threat. In contrast Ateniese et al . [15], [16] note that key confirmation for all users requires' at the very least, one round of simultaneous broadcasts', implying that it may be too costly to justify.

In [17], key confirmation is also defined as “Let U be a set of principals with Щ, Uj E Uк Key confirmation of Uj to Ui is provided if Uh has assurance that key К is a good key to communicate with every principal in , and principal Uj has received К . Complete key confirmation is provided to if key confirmation of is provided to U_t for all Uj E U \{UJ.”

In this paper we informally introduce a hierarchy of different group authentication schemes and also provide examples for each of these schemes. We also improve the key establishment protocol proposed in [10] to an authenticated version.

The rest of this paper is organized as follows: First, in section II we define different group authentication schemes. In section III , we review “The Skinny TRee

(STR)” protocol proposed by Steer et al . After that in section IV we propose an authenticated version of STR group key establishment protocol, and in section V we prove its correctness using Scyther. Finally, the conclusion is drawn is section VI .

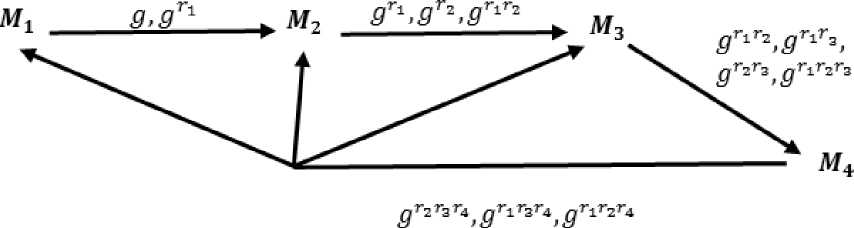
Fig.1. Group Diffie-Hellman (GDH.2)

We assume that M_n shares with eadi M( a distinct secret Kj

Round i: Mi-1                                 Mi rt e z; (r™1            )                                                  ( г"1)

^hi-i l./^¹»^4-^Jfr hf-i=S^ri "^r‘^-1                          p/ l^[l,i]|, 1ц=д^г1""^Tl

Round n:

MnM\Mj

ТЧ e z;

\Z^r‘ ^K* |ie[l,n] I

M_t calculates Z = fjZ^7-' "‘j

Fig.2. Authenticated GDH.2 Protocol.

• II.    Different Group Authentication Schemes

There exist many forms of group authentication schemes in the literature. In general in two partyprotocols, authentication means to assure the receiver that the message is sent by a specified sender and the message is not altered by a third party. In its most basic form, authentication is a simple statement about the existence of communication partners. We can roughly say that group authentication means that to assure every legal party that there exists no illegal party in the group, and all expected legal parties are alive in the group, and agree on some specific values.

In this section we propose a hierarchy of group authentication schemes and also provide some examples for each scheme.

• 1)    Authentication based on the Server

These types of protocols are based on a trusted server. The role of the server is authenticating and verifying the identity of each group member. In this way, everyone in the group would believe that there is no illegal principal in the group. Ateniese proposed a method to extend Group Diffie-Hellman key agreement. They proposed three version of it namely GDH.1, GDH.2, and GDH.3 [19]. After that they proposed an authenticated version of GDH.2 [15], [16] protocol to provide authenticated group key agreement. At the first we illustrate GDH.2 protocol, then explain the authenticated version of this protocol, AGDH.2.

Initialization : Let p be a prime and q a prime divisor of P -1. Let G be the unique cyclic subgroup of ℤ ^∗ of order Q , and let g be generator of G . Let = { M 1, M 2,…, Mn } be the set of users who want to share a key Z .

The protocol consists of two phase. In the first phase Mt receives i values from ^l-l. one of these values is the principal value ℎI_2_ =     …    while the remaining i-1 values consist ofmi-l with one of the exponents ^*1 , ^*2 ,…,T^_2. `missing'. Initially M^ starts Phase 1 by sending gT^ and g to A^?2 . On receiving this message M^ raises all received values to its exponent Ti to form i new message components and also includes the principal value ℎ£_in the message sent on to Mi+i .

The second phase of GDH.2 consists of a single message broadcast by Mn , which includes all the partial calculations necessary for each other M^ to find z with a single exponentiation using ri . On receiving the final message in the first phase, M„ can calculate the shared secret from the principal value hn_ г as Z = h„_ t — gT1T2 -rn. The final broadcast message can be calculated by Mb by raising each of the other n — 1 components of its received message to its secret exponent rn . An example of GDH.2 for four users is shown in fig 1.

In Authenticated GDH.2 protocol fig 2, M„ is assumed as a trusted server. Ms shares a unique secret with each member. In this way, only     authenticates other members of the group, and every other principal Mte{ 1,2 „_ц believes that there is no illegal member in the group based on his trust on .

• 2)    Authentication all Member of the Group

In this scheme, every group member verifies the identity of all other members in the group at once. In other words, every user can verify the whole group and if there are some illegal users in the group we cannot find them; and the only thing we know is that there are some other users in the group. For example, Klein [20] proposed a protocol which is based on this type of authentication. In their protocol each message protected by digital signature of the sender, which also include a unique identifier for the protocol run. Also each intermediate value is calculated multiple times with the aim of detecting and recovering from errors caused by principals deviating from the protocols. Their protocol is as follow:

Suppose M = [M₁, M₂ , — , M „ ) be the set of users who want to share a key K. There are n — 1 rounds to the protocol during which messages are broadcast, via a write-only bulletin board, to all other principals. Messages all consist of triples of the form (M ,, A,Sig_M (PID,g^A)), where PID is an identifier, A is a set of users in , and is the set of exponent input by the users in A. For example, a particular message sent by M 2 , might be (M 2 ,{ M₃ ,M 2 }, Sig m₂ (PID, g^ ^r9).

Round 1: Mc chooses random ephemeral input xt and broadcasts the triple (M_t, [MJ, S ig_M1(PID,g^Х1)У

Round (2 <  j <  n — 1) : The following steps are taken.

• a)   Mc collects all messages from round j — 1 that

exclude in the exponents. For each of these , raises the value to the exponent , and form a new message triple (adding its identity to the set A ) and broadcasts the result.

• b)    Each message with the same user set A is then compared. If there are any differences then the recovery process is invoked.

• c)    Once these are resolved, all duplicates are deleted and is incremented.

The recovery protocol has as input a set of principals and a set of message triples using set but with differing values of . All principals belonging to are required to reveal their secret input which allows checking against the signed inputs from the previous round.

Principals found to have been cheated by a majority of the other principals are expelled from the conference. Those principals who have not cheated choose new values and reconstruct their inputs for the current round.

For another example, propose a protocol based on the RSA cryptography. Suppose that N — pq ( p, q are tow distinct prime numbers) be an RSA modulo. Let M — [M₁, M₂ , . , M „ } be the set of users who want to share a key К . and ( e , , d) be public-private key of M_t and similar to GDH.2 M „ is assumed as a trusted server.

In this protocol Fig. 3, look like to process of GDH.2 users shared key with using their private key, , instead of their random value, . Therefore a shared key K — gdid ₂ . d „ , in which g is the generator of group G.

Round i (0 < i < n): Mt                 «M

• 5    ^di |/e[l«]L ^V*.

Round n:

M_n                                All M_t

Г dy-d,,         1

я “i |!е(1л]

• Fig.3. Protocol based on RSA

For authentication every user can easily check that .  — and deduce that the other parties are the intended communication partners.

• 3)    Authentication with dynamic trust

In this scheme, at first, it is assumed that the first member of the group is a trusted party, then he/she authenticates the second member of the group. If the first member of the group authenticates the second member, then the second member authenticates the third member of the group, and the protocol proceeds in this way.

In the next section we propose an authenticated version of STR protocol that meets this authentication scheme.

• 4)    Complete Authentication:

In both above aforementioned schemes, the authentication is obtained based on having a trusted party. But in practice, it is a very ideal assumption to have a trusted party. In complete authentication schemes, each two member of the group authenticates each other. In comparison to authentication all member of the group scheme, in this case if there are some illegal users in the group we can detect them since, we are authenticating each member one by one.

Let [M1, M2 , . , M„} be the group who are about to share a secret key. This group satisfies complete authentication if every pair (  ,   )       of the group members authenticate each other.

Ateniese et al. [15] proposed group Diffie-Hellman with complete key authentication (SA-GDH.2).

• 5)    Common Authentication:

In complete authentication everyone authenticates separately all members of the group, but he/she has no information about the process of authentication of other members of the group. Common authentication satisfies this property. In other words, if M — [ M ■, ,M₂ ,... , M „ } is the group, then every member ME M, knows that the M — [MJ group has complete authentication.

The group key can be calculated recursively as:

k_t — (bk_t_ ₁) ^{r i} mod p

Where, is the blinded group key. All blinded keys are assumed to be public.

In this protocol, adversary can easily masquerade as a member of the group to the other members, since the identity of group members are not checked in the protocol.

• III.    STR Protocol

The Skinny TRee (STR) protocol, proposed by Steer et al. [4] and undertaken by Kim et al. [18], is a contributive protocol using a tree structure. The notations used to describe this STR tree are shown in Table 1.

Table 1. Notation

Symbol	Definition
p	Large Prime number
9	Exponentiation Base
Mt	Member of the group
IN,	Internal node at level j
ri	Mt ’s session random
bk(	Mt ’s blinded key (that is gT* mod p )
kj	Secret key of internal node INj

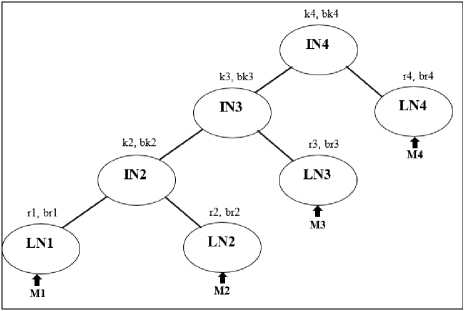
Fig.4. An example of STR

An example of STR protocol tree is shown in Fig. 4. where, to    are member nodes and    to    are internal nodes in tree structure. is the initiator of the group which is responsible for creating a new group. All internal nodes always have two children: one right leaf node and one left internal node. Each leaf node chose same large prime number and exponentiation base . Each leaf node has a session random chosen and kept secret by Mt The blinded version of this secret key is calculated as     —            .

The session random of first member acts as its secret key. In single node tree structure this session random acts as that is group key of single node group. The basic key agreement protocol is as follows:

Whenever    is the only member in the group it generates its own session random and calculates the blinded key. When new node joins the group, both members and calculate the group key as:

M₁ calculates: k₂ — (bIinded key of M₂ У¹ mod p

M₂ calculates: k₂ — (bIinded key оf М^У² mod p

Both of these calculate the same group key, and set the as their root secret key. This group key is used for the further group communication. Both members calculate the blinded group key and store in their root's blinded key field. In this tree structure any member can calculate the group key if it knows:

• IV.    Proposed Scheme

We propose an authentication protocol and add this to STR protocol to build Authenticated STR (ASTR) protocol which authentication is obtained with dynamic trust schema defined in previous section. Our proposed protocol is shown in Fig. 5.

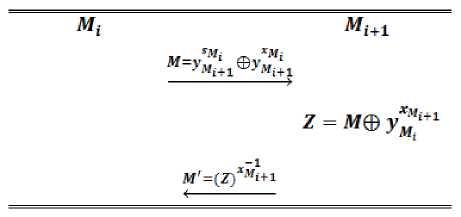
Fig.5. The Proposed Protocol

The notations that used to describe ASTR protocol expressed in previous section, in addition the symbol is the set of trust members in the group.

Our idea for authentication is to authenticate every one by previous user and then he/she add to the set of . With this notations blinded key of every user is used for generate secret key if and only if this user is a member of the set .

Suppose that, [M1, _,Mn} be the group that want to share a secret key, and suppose is trusted, therefore

— . At the first runs authentication protocol with M₂. If this run was successful, then M₁ add M₂ to the set

, afterward run STR protocol between and to generate k2 and bk2 (look at Fig. 4.), and then M2 similarly runs this protocol with and this protocol execute sequential between every Mt and Mi+i , for 1≤i≤n (if all run of authentication protocol be successful).

If identity of M₂ not verified for My (authentication protocol failed), then My ejects M₂ from the group, and continue this protocol with next member of the group M₃ . In other words My pending to the first Mj for 2≤ j ≤ n that Mj 's identity to be verified for him/her, then My adds Mj to the set T and then protocol will be continued with Mj similarly.

When the last member of the group authenticates (successful or failed), protocol ends, then the set T consist of all trust member in the group. And secret key shared with all member of the set T, in other word shared secret key calculated by all blinded key of users that they … are member of the set T (i.e к=    =         …     if and only if T=   ={M1 ,M2 ,… ,Mm}).

Therefore T , the set of trust member in the group, is dynamic, as we say in the Section II in the case 3, authentication with dynamic trust.

According to the above description is sufficient to propose our authentication protocol for M_t and M[₊₁ .

Authentication Protocol : Suppose that G be a group with high order p that solving discrete logarithm problem is hard in G , and g be a generator of G .

Let ( xMt , Ум^ =      ) and (XM^,, VMi+1 ) be private public key of Mt and ^i+1 . Mt choose random number s^ ∈ ℤ∗ and send M=     ⨁      to M[+1 , then

M_l+1 calculate z =   ⨁       and send back to M_t ,

M' =( z ) ^Mt₊₁ .

Therefore, M_t can easily check that M’ =      or not.

• V.    Security Analysis

In this section, we model and analyze our proposed protocol in the group with five users, by the Scyther verification tool [20].

Due to some limitations of Scyther, we had to impose some level of abstraction on our protocol. We have analyzed the correctness of our protocol in the case that five users are participating in the protocol.

Since, every two users M_t and Mj , can calculate the value of gX^j (by using his own secret key and the other parties public key), in order to simplify the protocol we consider this value can a shared key k ( M_t , Mj ) between M_t and Mj . Since, Scyther does not provide exponentiation we abstracted the term У^¹ by simply replacing this value by a freshly random number ^si-j .

If the other party is the claimed agent (i.e. he is user j ), then he can extract ^Si-j form k ( M_t , Mj ) ⨁ ^Si-j and sends it back to the users i .

The Scyther code of our protocol is given in Appendix A.

The results of running Scyther for five users is shown in Fig. 6. It shows that the aliveness, Ni-synchronisation, Ni-agreement, and the secrecy of the value Si-j are verified for three users and no attack is found within the two runs, in our protocol.

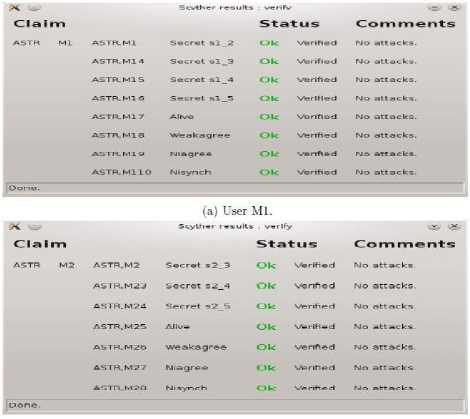
(b) User М2.

Verified

Verified

verified

no attacks.

Nisynch

Verified

Verified

Verified

(c) User М3.

Scythei

ASTR M4

Ok

ASTR.M41

Ok

Comments

No attacks within bounds.

No attacks within bounds.

ASTR.M43

ASTR.M44

Claim

Ok

No attacks within bounds.

Nlagree

Nisynch

Ok

ASTR.M51

A5TR.M52

A5TR.M53

ASTR M5 ASTR.M5

(d) User M4.
Scyther	results : verify
	Status	Comments
Alive	Ok	No attacks within bounds.
Weakagree	Ok	No attacks within bounds.
Niagree	Ok	No attacks within bounds.
Nisynch	Ok	No attacks within bounds.

(e) User M5.

Fig.6. Setup: Maximum number of runs = 2, Matching type = typed matching, Search pruning = Find all attacks.

• VI.    Conclusion

  Authentication is one the most important concepts in design and verification of security protocols. There are different types of authentication in literature. In 1997, Lowe suggested an “authentication hierarchy” and identified several possible definitions of “authentication”.

In this paper we informally categorized different schemes for group authentication in conference (group) key establishment protocols involving more than two party, and provided some examples for each category. We also proposed an authenticated version of “The Skinny TRee” (STR) protocol which falls into the “Authentication with dynamic trust” category of our hierarchy and proved it's correctness via Scyther.