A Novel and Improved Firefly Algorithm Based on Two-order Oscillation

Published Online May 2017 in MECS

• I.    Introduction

  Originated by bioluminescence, a new heuristic intelligence algorithm— firefly algorithm (FA), was developed by Dr. Xin-She Yang at Cambridge University in 2008 [1], with many similarities with other algorithms which are based on the so-called swarm intelligence, such as the famous Particle Swarm Optimization (PSO)[2], Artificial Bee Colony optimization (ABC), and Bacterial Foraging (BFA) algorithms, it is indeed much simpler both in concept and implementation. Due to its excellent performances, FA has been widely applied to many optimization fields, including optimization [3-4], data mining [5] and digital image processing [6] and so on.

However, one of the major drawbacks of FA is its premature convergence, especially when to handle problems with more local optima. Several attempts have been made to improve the performance of the basic FA to solve many optimization problems in different fields. Such as Luleseged and Hong Choon Ong et al. [7] modified the random movement of the brightest firefly that in some generations, when the current best position does not improve, may decreases its brightness. The proposed modification tries to improve the brightest firefly position generating the m-uniform random vectors and moves it in the direction of the best performance. In 2013, by replacing absorption coefficient and randomization parameter with modulo function of Gaussian distribution, Leandro dos Santos Coelhoa et al. proposed a method to avoid fireflies into local optimal locations, which has improved performance of firefly algorithm in chiller loading for energy conservation [8]. In 2014, Adil Baykasoglu et al.[9] has proposed an improved firefly algorithm with partial random restarts and an adaptive move procedure to solve dynamic multidimensional knapsack problems. For improvement of power quality in active power conditioner, Masoud Farhoodnea et al.[10] proposed a modified firefly algorithm with a tangent hyperbolic sigmoid function to update locations of fireflies; Similar to particle swarm optimization, global optimal location and individual optimal location ware drawn into firefly algorithm by M. Gnana Sundari for adjustable DC sources in 2015 [11]. In 2016, M. Gnana Sundari et al.[12] has proposed a self-adaptive firefly algorithm through improving the random parameter α to optimize the angle of multilevel inverter with adjustable DC sources. Although those proposed methods could avoid fireflies into local optimal locations in a way, however, more parameters have to be set and controlled in proposed method, which increase complexity of algorithm. In addition, related mathematic derivations weren’t given in most of literatures. So in this paper, an improved firefly algorithm will be explained with the stable theory of dynamic system and six typical functions will be used to verify performance. The simulative results indicate this modified firefly algorithm has excellent performance than standard one.

So the construction of the paper is: a vast literature survey has been conducted to review the state of the previous developed methods in section I; and in section II and section III, the basic theory of standard firefly algorithm is introduced by mathematical derivation. The stability of that will be proved. And the improved firefly algorithm will also be proved and deduced with two-order oscillation.

• II.    Firefly Algorithm

In this section, the basic theory of firefly algorithm will be introduced in detail.

In the process of optimization in firefly algorithm, the optimized result can be got via the progress of the position update, respective attraction and lightness of the fireflies [13-14]. The process of finding optimal solution is presented by the process of the fireflies searching the better locations in the solution space. Two important parameters are mentioned: the light intensity and the attractiveness. For simplicity, the following three idealized rules should be observed [15]:

• 1:    All fireflies will be attracted to other regardless of their sex;

• 2:    Attractiveness is proportional to their brightness, thus for any two flashing fireflies, the less bright one will move towards the brighter one.

• 3:    The brightness of a firefly is affected or determined by the objective function.

In the simplest form, the light intensity I varies according to the inverse square law:

i = I 2                         (1)

^rij ²

Where I is the intensity at the source. In order to avoid the singularity at r = 0 in the expression (1), the combined effect of both the inverse square law and absorption can be approximated as the following Gaussian form:

I = I o * e -' r ij                       (2)

Where I_o is the original light intensity ( r = 0 ) and у is the light absorption coefficient, у e [0. » ] .As a firefly’s attractiveness is proportional to the light intensity seen by adjacent fireflies, we can now define the attractiveness ^в of a firefly by:

в = в о * e ² ij                     (3)

Where в is the attractiveness at r = 0 . The distance between any two firefly i and j at x_i and x , respectively. The Cartesian distance is defined as:

d rj = lr -rA = A ^(Xi’k -xj,k)2           (4)

• V k = 1

Where x_{i , k} is the k -th component of the spatial coordinate x of i -th firefly.

The movement of thei -th firefly is attracted to another more attractive (brighter) the j -th firefly is defined by:

x i ( t + 1) = x i ( t ) + в ( X j ( t ) - x i ( t )) + a (rand - ^)   (5)

Where x, ( t + 1) represents the position of the firefly i after t + 1th movement; On the equal mark right, the second term is due to the attraction, while the third term is randomization with a being the randomization parameter, a e [0,1]. For most problems, rand is random number which are drawn from a Gaussian distribution.

• III.    The Design of Firefly Algorithm Based on Two-Order Oscillation

In this section, the improved firefly algorithm based on two-order oscillation will be described.

In the process of optimization, fireflies will move to brighter those, according to two important parameters: the light intensity and the attractiveness. The updated formula of locations is showed as following:

x i ( t + 1) = x i ( t ) + в ( X j ( t ) - x i ( t )) + a ( rand - ^)   (6)

Assuming that the j -th firefly with the t -th iteration is brighter than that i -th firefly, random is added to avoid fireflies into local optimal locations, it can be regarded as a bias in iterative systems. So the formula (6) could be rewrote as following:

xi(t+ 1) - xi(t) = e(xj(t) - xi(t))

The above could be regarded as difference formula of Euler for x_i ( t ) and x ( t ). So, its differential formula is:

dx^(t) = -ex (t) + ex,(t)(8)

dt

So it could be rewrote with Laplace transformation: sx, ( s ) + e x, ( s ) = e ^j ( s ) , and is also explained:

^v) = Л(9)

xj(s)

As is showed above, it could be regarded as a one-order inertial system, and x(s) and x(s) are the import and export of that, respectively. Since the iteration increasing, the export x(s) will converge towards to x(s), which means the conventional firefly algorithm has convergence in a way. However, this method just with inertial convergence couldn’t balance searching step and searching accuracy, which may lead fireflies into local optimal locations. Hence, the convergent method is replaced with two-order oscillation in our paper. The proposed method is showed as:

xi ⁽ t + 1) = x i ⁽ t ) + P ⁽ x j ⁽ t ) ^{- (1} + Ф ) x i ⁽ t ) ^- № ⁽ t ^- D)' ^s

Where s = a (Rand - 0.5); x, ( t - 1) is location of the i -th firefly at ( t - 1) -th iteration. And ф is defined as balanced coefficient. At former period of iterations, ф could be selected in (0, 2^ —¹ )for big searching step;

and it could be set: ( 2 —1, ³⁽² —1)) at later period of iteration.

balanced coefficient could be selected in (0 2—1) at ’ в former period of iterations. At later period, this system should be in over damping state for small searching step and high precision: (вф +1)2 - 4 в > 0 and -(вф +1) < 0. After numerous experiments, it can be set

• ² jp -1 3(2 y e -1) .

n(             ,                  ).

в     2в

Derivation and Proof:

In a similar way, the formula (5) can be rewrote:

x i ⁽ t ⁺ 1) ^- x i ⁽ t ) ^{- (} x i ⁽ t ) ^- x i ⁽ t ^- 1))

= ^{в (} x j ⁽ t ) ^{- (1 +} Ф ) x i ⁽ t ) ^- Ф Х ⁽ t ^- 1)) ^{- (} x i ⁽ t ) ^- x i ⁽ t ^- 1))

• IV. The Simulation And Experiment

In this section, the original firefly algorithm proposed by Xin-She Yang will be regarded as standard method to test with six different functions and compare with our improved firefly algorithm using MATLAB/Simulink. And we could explain and verify the feasibility and effectiveness of our proposed method.

• A. Six Tested Functions

The efficiency and performance of the proposed method with the following six nonlinear functions (11-16) are evaluated:

So, xi (t +1) - 2xi(t) + xi (t -1)

= - в ( ф + 1) X i ( t ) - X i ( t ) + фP X i ( t - 1) + x i ( t - 1) + ф X j ( t )

= ^- Mxi ⁽ t ) ^- xi ⁽ t ^- 1)) ^- ( xi ⁽ t ) ^- xi ⁽ t ^- 1» ^- Pv ⁽ t ) ⁺ ^ xj ⁽ t )

So the differential formula of above is:

d ² x_i ( t )                dx _i ( t )

—~2— = ^{-( вф +}1) —--- ^{в x}i ⁽ t )⁺ P ^xj ⁽ t )

dt ²                  dt

The Laplace transformation of that is:

s ² Xi ( s ) + ( вф + 1) SX i ( s ) + e x i ( s ) = e x j ( s )

That is:

f(x , y ) = e^{x - 4)} 2 ^{- (} у ^{- 4)} + e - ^{x + 4)} 2 ^{- (} у ^{- 4)} 2 + 2[ e ^{- x 2 - y 2} + e ^{- x 2 - ( y + 4)} 2 ]

Where ( x , y ) e [ - 5,5] x [ - 5,5]

sin( Jx ² + y ² ) ^cos(2 " ^{x ) + cos(2} " ^y ) f ( x , y ) = — 7    ^{7 2} + e     ²       - 2.71289

²       4*+У7

Where ( x , y ) e [ - 2,2] x [ - 2,2]

22    2

f з ( x , y ) = e"^{sm x - cos y} + 2 e "^cos

x - sin ²

y

Where ( x , y ) e [ - 2,2] x [ - 2,2]

xi( s) =        в xj (s)  s2 + (вф + 1) s + в

The above formula could be regarded as a two-order Oscillational system.

So when s ² + ( вф + 1) s + в = 0 , two solutions are:

^f 4 ^{( x} , y ) = 0.5 -

sin ² «Jx ² + y ² - 0.5

(1 + 0.001( x ² + y ² )) ²

Where ( x , y ) e [ - 200,200] x [ - 200,200]

_ - ( вф + 1) ± V ( вф + 1) ² - 4 в

A ¹’² =                2

For big searching step and fast convergent speed, the system could be underdamping state and be convergent. So, ( вф + 1) 2 - 4 в <  0 and - ( вф + 1) <  0 , that is, the

n f =^( x2-10cos (2nx8) +10)        (15)

i =1

Where - 5 <  x^ <  5 .

n f6 =JX xi

V i =1

Where - 4 <  Xg <  4 .

Function f is the four-peak function as illustrated in Fig.1(a), which has two local peaks with f = 1 at ( - 4,4) and (4,4) , and two global peaks with ^_ж = 2 at (0,0) and (0, - 4). Function f is showed in Fig.1(b), which has many local maximum and one global maximum f =1 at ( x , y ) ^ (0,0) .Function f has two local maximum and two global peaks with f_mж = 2.135 at (1.6,0) and ( - 1.6,0), which is showed in Fig.1(c). Function f ₄ is the Schaffer’s function as illustrated in Fig. 1(d), which has infinite local maximum and one global maximum at (0, 0) , and f = 1 . Opposing to f , f , named Rastrigin, has same innumerable local maximum and minimum points, and one global minimum point is (0,0), that is, f_Smin = 0; The sixth functions is Sphere function, liking a bowl, has one global minimum location at (0,0) . When function lies this point, the global minimum value could be got, that is, f_6nin = 0, as is shown in Fig.1.(f).

• B.    Discussion and Analysis

Fig.2 has showed final locations of fireflies for different functions with stand and proposed method, and the relevant parameters are followed: In f~ f,the population size of firefly and the max iterations are 12 and 50, respectively;Tab.1 has presented optimal locations found by fireflies. As we can see from Fig. 2(a) and Fig. 2(b), all fireflies have moved to two global peaks oppose to six fireflies got in local maximum value, although the precision is similar to standard method. In function 2, all bodies have come to a local optimal location, unfortunately. However, the global optimal location can be easily found after several iterations. As for function 3, only one global point could be found and others have moved to local optimal point, mistakenly. Compared to it, our proposed method still has excellent ability to recognize and find two global max locations. Likewise, the optimal point could be found facing to function 4 with infinite local peaks. In Fig.2(i) and Fig.2(j), While the optimal point couldn’t be found in spite of several iterations, that point can be easily identified, that is, 0.1466, opposing to standard mothod with 5.0538. As we can see from Fig.1(k) and Fig.1(l), almost of all fireflies have moved to the only minimum location, no matter standard method or proposed that. Compared to 0.098 of former one, however, the latter minimum value 0.012 is more close to actual minimum value f ,min = 0.

• V. Conclusion

This paper has focused on an improved firefly algorithm based on two-order oscillation. Mathematical deduction of standard firefly algorithm indicates it has convergence performance in a way. A firefly will move to more lighter one with one order inertia process, which may lead to premature convergence, that is, local optimal locations. So the update method of one-order inertia is replaced with two-order oscillation, and range of balanced coefficient has been given to balance searching step and searching accuracy. The simulation results show that proposed method realizes more excellent performance to prevent individual into local optimal locations and obtain high accuracy than conventional method.

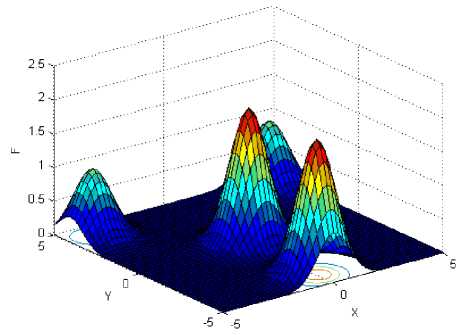
(a) f 1

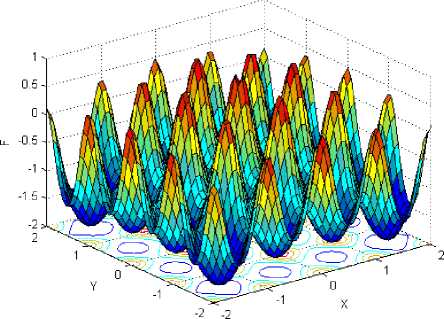
(b) f 2

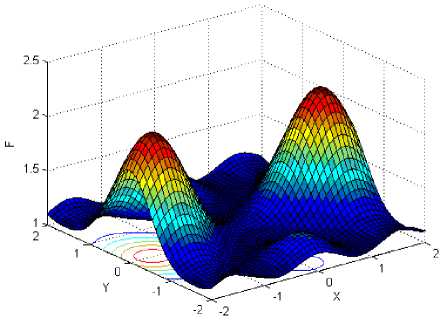
(c) f 3

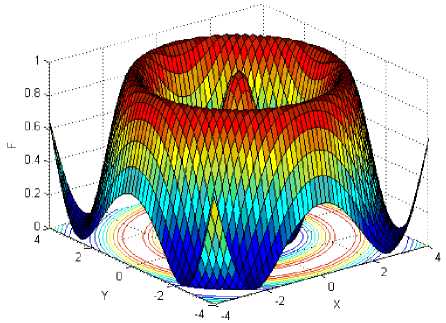
(d) f 4

(e) f 5

(f) f 6

Fig.1. Six Tested Functions

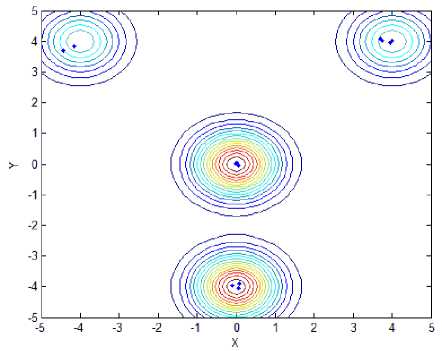
(a) Locations of fireflies for f 1 with standard metho

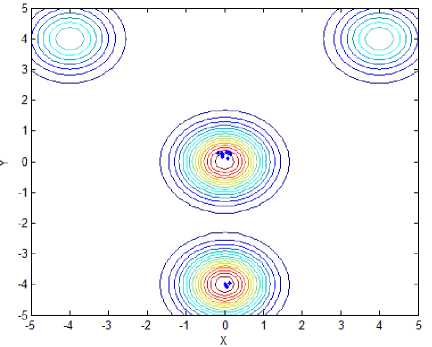
(b) Locations of fireflies for f 1 with proposed method

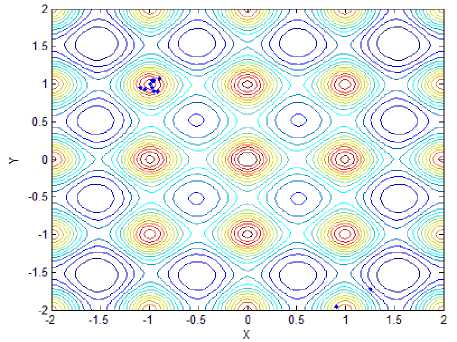
(c) Locations of fireflies for f 2 with standard method

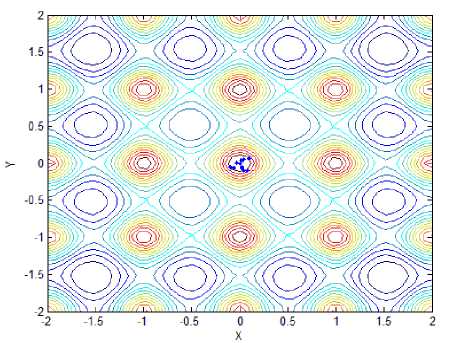
(d) Locations of fireflies for f 2 with proposed method

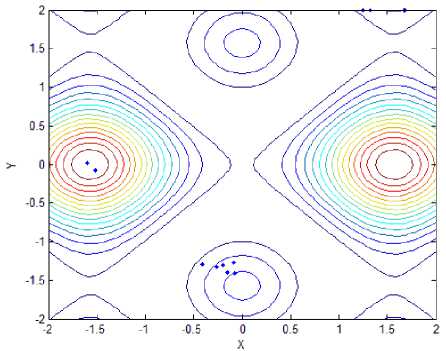
(e) Locations of fireflies for f 3 with standard method

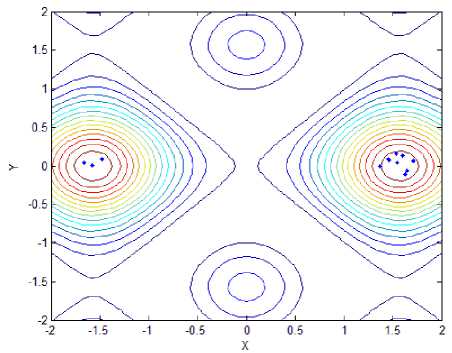
(f) Locations of fireflies for f 3 with proposed method

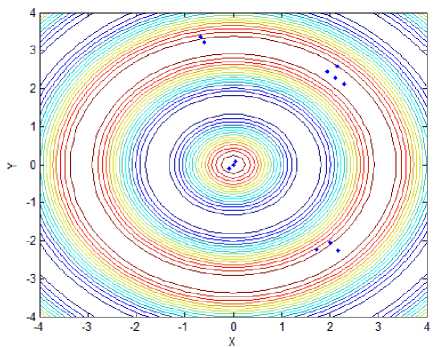
(g) Locations of fireflies for f 4 with standard meth

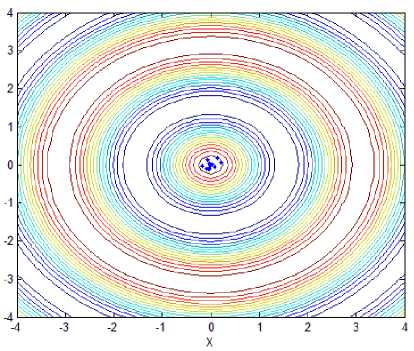
(h) Locations of fireflies for f 4 with proposed method

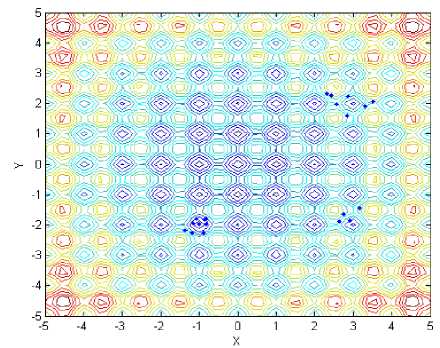
(i) Locations of fireflies for f 5 with standard method

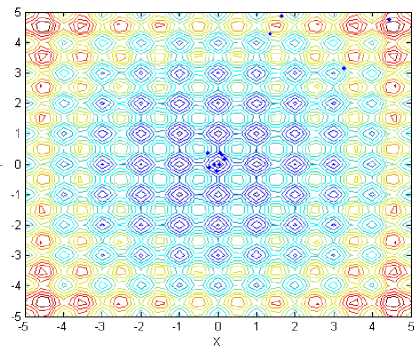
Locations of fireflies for f 5 with proposed method

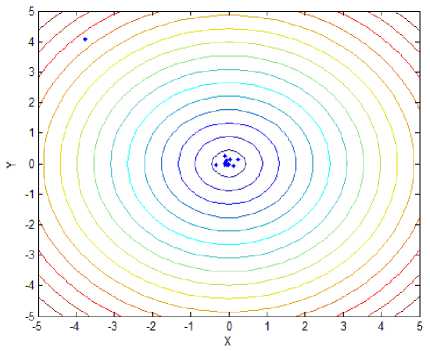
(k) Locations of fireflies for f ₆ with standard method

(j)

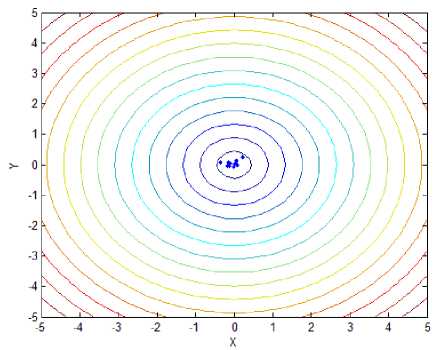
Locations of fireflies for f ₆ with proposed method

Fig.2. Locations of fireflies for f 1 ~ f 6 with standard method and proposed method

Table 1. Global max/min value for different functions with standard and proposed method

Functions	Methods	Global Max coordinate	Global Max/ Min Value
f 1	Standard method	(-0.0060, 0.0109),( 0.0580, - 4.0509)	1.9997, 1.9881
	Proposed method	(0.0778,0.0920),( 0.0051, -3.9995)	1.9712,1.9999
f 2	Standard method	(-0.9920,0.9978)	0.7048
	Proposed method	(0.0152,0.0016)	0.9991
f 3	Standard method	(-1.5955,0.0141)	2.1338
	Proposed method	(1.5464,0.0460),(1.5782,0.0051)	2.1303,2.1352
f 4	Standard method	(0.0157,-0.0030)	0.9997
	Proposed method	(-0.0081,-0.0043)	0.9999
f 5	Standard method	(-1.0125, -1.9803)	5.0538
	Proposed method	( 0.0262, -0.0073)	0.1466
f 6	Standard method	( -0.0027, -0.0094)	0.0098
	Proposed method	( 0.0011, 0.0006)	0.0012

Acknowledgment

This work was supported by the National Natural Science Foundation of China (61572416), Shenzhen significant strategy layout project (JCYJ20160429112213 821), and Hunan province Natural science Zhuzhou United foundation (2016JJ5033). HuNan University of Science and Technology Doctor Startup Fund Grant No.E51664 ， Hunan Provincial Department of Education Science Research Project Grant No.16C0639.