A Novel Approach for Effective Emotion Recognition Using Double Truncated Gaussian Mixture Model and EEG

Published Online June 2017 in MECS

Human-computer interaction is possible area of interest since the birth of computer era. The strides of computer interaction can be witnessed over the years from punch cards systems to keyboards and mouse. These developments in the human-computer interaction are mainly focused towards the design of a user-friendly and ergonomic system which is most efficient, and communication can be done with at most comfort [1]. These technologies are embedded with interfaces such as voice recognition, face recognition.

Technological updates help to offer a direct humancomputer interaction employing signals which are generated from the brain. These methodologies contribute to serve the people having Neuro-muscular disabilities, thereby helping them in recognition the people. These technologies, as it is known as braincomputer interaction, facilitate to control the application of the equipment using the signals generated by the brain during the thought process [2] [3].

The developments in the area of cognitive neuro– science have been instigated latest advancements in the field of brain-computer interaction in particular to brain image technology. The Electroencephalography (EEG) [4], functional magnetic imaging (fMRI), Magneto Encephalography (MEG) are mainly used for brain analysis among these technologies EEG, can be acquired cheaply and it is noninvasive which helps to identify the functional correlations in the brain. The EEG plays a critical as well as a vital role in recognition of the ideas actually from the immobilized persons. These thoughts (or) emotions play a fundamental or major role in understanding the inherent feelings of the other person. Emotions act as a stimulus that evaluates the other persons based on the experiences. The emotions generated from the mobilized persons can be easily interpreted and various methodologies exist in the literature to identify the emotions of the individual [8].

However, these emotions that are generated from mobilized persons are from acting sequences, where as in order to have the exact emotions of the individual, it is necessary to understand and interpret the thoughts using the brain signals for which EEG will be more effective.

The emotion recognition models that are presented in the earlier chapter may be restricted to mobilized persons only. To interact the emotions of immobilized individuals it necessary to estimate and evaluate the brain signals actually. This interpretation of the signal may be very much useful to understand the feelings of immobilized persons [6]. In particular brain disease, where the effectiveness of drug during the treatment can be identified by reading the brain emotions. The emotions are categorized into four major groups as in the case of mobilized persons viz, happy, sad, angry and neutral. If the brain signals from the EEG are interpreted as happy, in case of immobilized during the treatment in hospital, implies that he/ she is responding to the drug, and comfort level can be expressed via happy emotions. Therefore to interpret these signals, it is very much necessary to identify the brain signals effectively [7]. Hence in this paper we propose a novel approach using Truncated Gaussian Mixture Model to identify the brain signals whereby the emotions can be classified and the treatment can be addressed.

Outline of the remaining paper, section -2 gives a brief review on research work so far done for emotion recognition using EEG. Section -3 presents the gap observed in the research area based on the previous section. Section -4 presents the proposed novel approach. Section -5 presents the proposed system. Section-6 gives details on experimentation and results obtained. Section -7 presents the conclusion.

• II.    R elated W orks on E motion R ecognition U sing EEG

  Shuang Liu et al. (2016) used Power spectral density (PSD) and brain asymmetry (BAY) from EEG features and Support vector machine classifier. They were able to achieve 93.31% of accuracy rate for PSD and 85.39% with BAY. Tanfang Chen et.al. (2016) tried to recognize the emotions using DRBM by building the hidden relationship among the user profiles, EEG and emotion labels. Aravind E. Vijayan et.al (2015) used statistically weighed autoregressive modeling of Electroencephalogram (EEG) signals for emotion recognition and were able to achieve an accuracy of 94.097%.

Priyanka Abhang et al. (2011) have proposed a paper which specifies the used EEG brain signals and speech in various languages to recognize human emotions. Methods used are Emotion tracking and Higher Order crossings and Empirical Mode Decomposition. Techniques used for feature extraction are Independent Component Analysis (ICA), Mel frequency cepstral coefficient (MFCC), KNN method, and wavelet. Panagiotis C. et al (2010) have proposed a paper in which they have concentrated on recognizing the emotion based on EEG feature extraction and the basic concept neuron system was introduced. Here they consider a feature extraction scheme like higher order crossings analysis is active as well as robust classification method, it call as HOC-emotion classifier (HOC-EC),it was achieve testing four different classifiers in order to accomplish efficient emotion identification. Results include QDA has obtained 62.3% mean successful rate, for the mixture channel case, best results are obtained by SVM (83.33% mean classification rate).

Murugappan el at (2010) in their paper identified the human emotions with the help of wavelet transform using EEG signals. Here they are considering five different emotions namely natural, happy, fear, disgust, and surprise. 10-10 system which is having 64 electrodes is taken to collect EEG signals. Preprocessing is done with the help of SL filter. They are classifying the emotions with the help of DTW. KNN and LDA are utilized for performance evaluation and emotional state classification. The accuracy rate is 83.26%. Reza Khosrowabadi et al (2010) proposed a paper focuses on classification of EEG have shown a relationship on emotions with the help of features extracted GM of EEG spectrogram. Fractional dimension of EEG signal is compared with three feature extraction methods, for features extraction they are using KNN and SVM .In this paper they have investigated four different emotions, which include positive, negative calm and excited. Finally the features are extracted by using the Gaussian mixtures of EEG spectrogram. Ali S. AlMejrad (2010) has proposed a paper proposed a real time system to recognize the emotions with the help of EEG and they have discussed sensitivity activities in point of EEG measurement and noise removal and artifacts. They have extracted features with the help of wavelet transform and they have used different classification methods like SVM, Radial basis Function, Genetic Algorithm, Linear Discriminant Analysis.

M Murugappan et al (2010) proposed a paper focusing mainly on the people who are physically immobilized. They tried to establish a new communication medium for the immobilized people. Here they have adopted international standard video clips for identifying human emotions like happy disgust, fear and surprise. With the help of wavelet functions they extracted the statistical features of human brain signals (EEG). “Fuzzy C-Means (FCM) clustering” was used for the classification of emotion. The conclusion in this paper shows an encouraging result for detection of emotion. Murugappan.M et al (2009) in his paper anticipated a competent gaining protocol for gathering the EEG signals. For the pre-processing AMR method was used. For experimentation, they are taken six healthy people and 63 biosensors system is utilized. EEG parameters are extracted from discrete wavelet transform before we need to pre-process the signals. Using Fuzzy C-Means (FCM) clustering for the emotional classification purpose they derived Statistical features named as discrete emotions.

After a brief study of literature we come to a conclusion that very sparse research is done towards emotion recognition from EEG for immobilized persons. Hence in this paper an attempt is made to identify the emotional state of brain diseased persons.

shown in figure 1, figure 2 and figure 3.

• III.    G ap O bserved

The emotions are to be extracted from the immobilize persons, Nero Scans will be much useful, for which Electroencephalography (EEG) will be more useful, which refers to the measures of brain electric activity [9] [10]. The measurement of the brain electrical activity can be obtained by the placing the EEG electrode on the brain scalp. Several works have been reported in literature based on the physiological signals such as EEG, ECG, Skin conductivity, EMG and Heart Rate. Most of the literature available regarding the brain diseased persons / immobilized persons is subjected to the movement of the arm position or eye movements and no research is driven to understand the emotions of the immobilized persons, hence this paper is further extended to study the emotions by developing two different models and extracting the brain signals using the EEG [11]. The initial estimates of the model parameters of the Doubly Truncated Gaussian Mixture Model are updated using the EM algorithm. The emotions that are generated by the human brain are interpreted from the EEG signals using the limbic system. Various regions in the brain, that contribute in assessing the emotions include,

• 1.    Left Temporal areas: sadness.

• 2.    Right Prefrontal Cortex area: sadness, happiness and disgust.

• 3.    Bilateral Temporal activation: fear.

Apart from the above, all emotions share the areas viz., prefrontal cortex, cingulated gyrus and temporal cortex. In order to obtain the EEG signals, the subjects are to be trained, if mentally fit, then explained about the system positioning of the electrodes. Time duration should have a significant role in the extraction process; process should be done in the processes of trained technician. Fp1, FpZ, Fp2, F7, F3, F2, F4 and F8 electrodes are utilized to recognize the emotions. The brain signals from the diseased persons are extracted using the EEG, and the signals are preprocessed to minimize the noise and the amplitude signals are extracted which are normalized into different ranges basing on the rhythm, for the dimensionality reduction [13] [14]. These features extracted are modeled using the Doubly Truncated Gaussian Mixture Model and the Probability Density function of each rhythm is extracted, for each of the emotions that are exhibited the subject, the Probability density functions are calculated and basing on the Maximum likelihood estimate of each signal, the emotions are classified [15] [16].

• IV.    P roposed M odel : D ouble T runcated G aussian M ixture M odel

Using Doubly Truncated Gaussian Distribution Model is that, the infinite range of the EEG samples can be truncated between a certain limits and the recognition of the emotions can be carried out using the finite range as

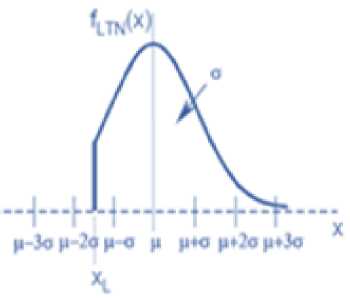
Fig.1. Left Truncated Normal Distribution

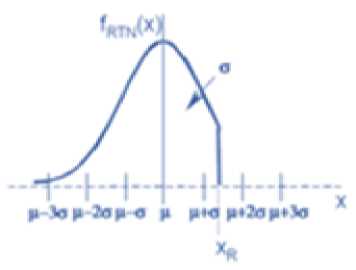
Fig.2. Right Truncated Normal Distribution

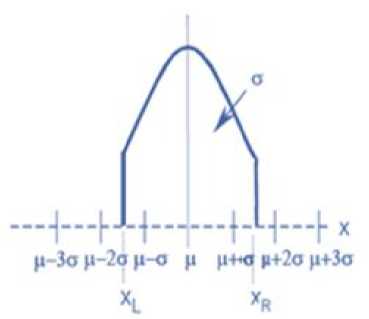
Fig.3. Doubly-Truncated Normal Distribution

• A.    The Probability Density Function (PDF) of GMM

The PDF of GMM is given by equation (1)

f ( z ) 2E^

-н z - p. I e 2 l a ) ; -ОТ < z < +OT, 0 < CT

The value of Z below some Z L and above some Z M cannot be possible to exist. Then the resulting distribution is a Doubly Truncated Gaussian Distribution and the PDF is given by equation (2)

, x        g ( z )

g ( z ) = -Z--------- , -to <  z < to

J V(z) dz

ZM

k h (Zs ;6 ^Zag (Zs ,6)

i = 1

Where Z_L <  Z <  Z M and Z M <  Z < to

N

This implies g ( z )

f ( z )

-1 [ Z - M , 1

V"¹   2 I ° J

/ ^a E— z    7

^= 1*   л/2 П° ( B - A )

B - A

, Z L <  Z <  Z,

Where,

The conditional probability of any observation Z j to belong to the segment k as

Z L

A =1

-to

e

ZM

dz and B = J

-to

e

dz

t k ( Z s ;6 ) =

« k g * ( Z s , 6 ¹ ) _    a k g k ( Z s , 6 )

^h ( Z s ; ⁶ ) Z ‘^g^ ( Z s , 6 )

Therefore,

g ( ^z ) = у

Z

У 2 n° e

k

Since h ( Z_s ; 6 ¹ ) = Z “ k g_k ( Z_s , 6 ) from equation i =1

-to

-to

1        - 1 f z - ^ '1 2

² 1 ° J dz

_ V var ( z ) c = ^E ( ^Z )

The lower and upper truncation points are Z L and Z M respectively.

• B.    Estimation of the model parameter using ExpectationMaximization Algorithm

The likelihood function  of  sample observation

{ Z j, Z ₂,..., Z _n} drawn with the  Probability Density

Function h ( z, 6 ) = Zag, ( z_s, 6 ) is given in equation (5)

Evaluating the expectation value L(0) is

Q ( в^ ¹ ) = E ₆ { log L ( 6 ) }

Following the heuristic arguments of Jeff. A Bilmes (1997) we get kN

Q ( 6;6 l ) = ZZ E l { t - ( Z6 ) (log g * ( Z , 6 ) + loga , ) } ⁽¹¹⁾

L ( 6 ) = n N

(

Z a g ( z s ^{, 6} )

N

k

Z a       e

-i = 1   У 2 n° ( B - A )

2?

But we have g i ( z; 6 ) =

M. z^,6 )

B - A

Since here the distribution is truncated.

^Where f ( z , ⁶ ) =       e

Where A and B are given above.

Therefore,

log ( ⁶ ) = log ^ « , g , ( z s ^{, 6} )

kN

^Q ( ^{6 , 6 ( 1} ) ) = ZZ ^{E ( 1} ) { t - ( ^{z, 6} ) ^(log g - ( ^z ; ⁶ )^{+ 1o}g“ - ) }

N    <  k

= Z ^log Z ^a - g i ( z s , ⁶ )

Substitute the value of log g _z ( z ; 6 ) we have

E step:

Q(6,6(0)) = E^ {logL(6)/z} sN

ZZ E ^{( 1} ) { t* ( z ’ 6 ) (log f ( z ; 6 ) - log ( B - A ) ) + loga i }

Given the initial parameters 0^;, one cam computes the density of any observation Z _s as

M- Step: The problem of calculating the maximum likelihood estimation of the segment weight a^, under the additional condition

k

Eg = 1 can be solved by i=1

applying the standard solution for constrained maximum. We construct the first order Lagrange-type function.

E ^ ( t_k ( z , , 9 ) ) = Xa _k       (20)

- = 1

L = E ^{( l} )

k log L (9) + X(1 -^al i=1

Taking sum all over k=1,2,3…k and considering that for every z_s, the sum over all t_k ( z_s, 9 ) must be equal to ONE, due to the probability character of t_k ( z_s,9 ) we

get

Where λ is a Lagrangian multiplier combining constraints with log likelihood function to be maximized. The derivative of L kN

EE t . ( z , 9 ) - X = — i = 1 - = 1

JL = о >  E ( ^l )

8a _k         da k I

log L ( 9 ) + X (1 - У ^L^

1=1 0« k

= 0

Therefore a ^ ^{+ 1}

N

= — E ^E { t k ( Z , ^ ) }

- = 1

This implies

We have

N

E

- = 1

У ^k E ^{( l} )

Z—i i = 1

d

^da k

ZM

E^l { t k ( Z - , 9 ) } = J a k

Z L

Ф

Multiplying

E - (  )

k

E E ^{1 1 1}

I = 1

g k ( ^z- , ⁹ ) ) h ( z - , 9 )

- X = 0

- X = 0

and dividing by a we

J_ ^, E^la k g k ( z - ,9 )) ^a k ^E    h ( z . , 9^l )

- X = 0

have

This implies

N

— \e ( t k ( z , , 9 ) ) - X = 0 ^a y - : r

gk (Z-,9)  h(Z-,9)dz h (Z-, 9)  \MMh (Z. ,9 ) dz

Z L      ^s

Therefore _a ^ + 1 = _L У________ a k_________

^{N E} H ( Z_M , ^ ) - H ( Zl , ^ )

where         H ( Z_M,^ )   J a i g i ( Z . ,^ ) dz        and

-X

Z L

H ( Z l , 0 ^l ) = J a i g i ( Z - ,^ ) dz

-X

For updating ц : for updating the parameters, ^ , k=1,2,^ k. we consider the derivation of Q ( d , 0^l ) with respect to ^ equated to zero.

⁵ Q ( » , ^{e l} ) ₌₀

5 ^ k

Where

To update the estimates of a ^ we have to go next level, i.e, a ^ ^{+ 1} we have,

N

— E E^l ( tk ( z_s , 9 ^l )) = X ^a k s = 1

to the

kN

^        E E e ^{( l} ) { t i ( z . , ^ ) (log g i ( z ; ^ ) ) + log a. } = 0 (23)

° ^ k *= r : = r

By taking expectations from equation (10)

I.1

УE(l) j ti (z-, yl       (log gi (z; 9)) [ = 0(24)

,=1    I        /5^kJ

This implies

But we have

(log g k ( z ⁹ ) ) = log

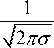
- 1

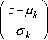
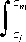
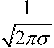
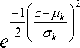
dz

J " ^ fk ( ^{z - 9} ) ^dz " zl ^ak ________________

J "fk (z,9)dz zl

Therefore

H k ak ²

And г^(log gk (z9)) =

в dHk

-log 22--log m -1iHk)2 -log J k 2 a kz

_ ^J' ^ak² f k ⁽ z ’ ⁹ ) dz    \ H k o_ I ^{f ( z}" ^{)- f ( z}i ) L H k If ^{f ( z}" ^{)- f ( z}i ) )

fzf (z,9) dz        L at2 at2 [ В - A j at2 ] [    В - Aj

The equation becomes

⁸ л      (          1 /            ^f ( z " ) - ^f ( z l ) )

— (log gk ( Z;9 )) =—( z - Hk ) + | ---— I dHk             ak         к   B - AJ

This implies

This implies that

Ф

(log g k ( ^z ; ⁹ ) ) =

( ^{z -} H k )

f ^f ( ^z" ^{)- f} ( z l ) ) _a 2 к в - A J k

a k ²

J "      fk ( ^{z - 9} ) ^dz

— (log gk (z ;9)) = — (z - Hk) —"k--------- ak2            f^ (z,9)dz zl

There from equation 24, we have

V N E ( l ). ^ s = 1

tk

( ^zs , ⁹ l ) ( ^{z -} H k ) ^-

f ^{f ( z}" ^{)- f (} z l ) ) _ 2 к В - A J ^k

^a k

We have —— ⁸ H k

This implies

This implies

= 0

a k² ^Tf ^fk ( z ^ ) = z^f k ( z ^ ) — ^Ц к f k ( z , 9 )

X S = 1 E ( ^l ’ {[ t k ( z s , 9 l ) z ]+ E N = 1 t k ( z s 9 ^l ) [ f ^ zf j a _t 2 } X N = 1 E ( ^l ) t k ( z .^{- 9} )

This implies

The first term of the equation is zfk (z-9) = Hkfk (z,9) + a2 2^ fk (z,9)

zm

El'[tk (z.-9 )z] = f zl

^z « k^l g k ( z s ^{, 9} l )

dz f h(zs,9)dz

The second part of the equation

J "  f z-^ к fk ^{( z} , ⁹ ) ^dz    V^'zifk ( z - 9 ) dz J " ^fk ( z , 9 ) dz

1 zi к ak   JJ z, ak 2                J z, ak f "f (z,9) dz                 f "fk (z,9) dz         f "fk (z,9) dz z,                                     [       z,                                   z,

^a k

=>--

2 f ^f ( ^z " )^{- f} ( ^z l ) ^: I       В - A

J z " ^{h (} z . , ⁹ ) ^dz

The second term of equation is

Since

zm

I zfk Iz-9)dz(

"____________= H + a2I f (z") f (zl) I and z"                       f     B — A fk (z,9)dz           кJ zl

2 I f (ZM )- f (ZL ) j ZM akgk (Zs ,9 )dz k к     B - A     J ZL JZMh (Zs ,9 ) dz l2

^{f (} ZM ) ^{f (} ZL ) j_______ 1_______

B - A     J J ZMh ( Z_s , 9 ) dz

The denominator of the equation (35) can be simplified as

J " z^r fk ^{( z} ; ⁹ k ) ^dz

^J zl ^dak _______________

E

« k

f "fk ( ^z ; ⁹ k ) ^dz z_l

Hence

“ k

A ⁺ 2 ° t'

A + 1

ZM h (Zs ,9) dz

Z L

f ( Z M ) - f ( Z l )

B - A

ZM jz h (Zs, 9) dz

ok

j Z M h ( Z , 9 ) dz

Therefore

f ( Z m ) — f ( Z l )

B - A

For updating ^ ² :

For updating ct^ ² we consider the derivative Q ( 9 . 9 ^l ) with respect to ct^ ² and equate it to zero.

of

2 Q ( ⁹⁹ ) ^d° k

kN

--yZ Z E д 0 k ² i = 1 s = 1

⁽ ' ⁾ ti i ( zs ^{, 9} ) ^(log ft ( ^{z 9} ) ^{) + l}og « i }

= N E ⁽ 'Ц4 ( z_s. 9 p^y(log f_k ( z; 9 ) ) >  s = 1      [ ^{У         2}                 ,

This implies

N ( l )

Z E 1

s = 1

^{- lo}g j fk ( ^{z 9} ) ^{dz + l}°g « k

. 2 I

z ; 9 k ) l      -I z-A II dz

V ^a k   V ^a k ))

J "fk (z ;9k)dz zl

*ZM     fk (z ,9k)dz

ZL, ^d a 2

* ZMfk (z ,9k)dz

- 1

——1- ( 1+ a ) B - A   ^{v k}'

fk ( zl . 9 ) - fk ( zm , 9 )

B - A

ZMfk ( Zm . 9 ) - ZLfk ( Zl ,9 )

B - A

Substitute equation (18) in equation (24) we get

d Q ( ef l ) ⁵ ° k

= N El f tx s = 1 ^V

Л 2 Z - a

[A z ^{2 a} k V ^a k J

11   1

T+

2 0 2 ² O 2 ² O 2 ( ^B - A )

1 + A k f fk ( ZL ⁹ ) - fk ( ZM , ⁹ )

B - A

1 fk ( Zl 9 ) - fk ( Zm 9 )_n

A      B - A     ¹

^kV^s .        2

I zl

Let

D = B - A [ ( ^{1 +} A k ) ( fk ( ^Z L ⁹ ) - fk ( ^Z M ⁹ ) J+f ZMfk ( ^Z M ⁹ ) - ZLfk ( ^Z L ⁹ ) J]

Implies

N

ZE (t. (z.9'))

s -1

Z - M I "04b )

D

= 0

N

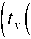
The second part of the equation i.e,

2 Z - M I 2 0 4 J

ф

_Т?¹ * ^{1 )}

X , ч E ( t > ( ^{Z , e} ) ) ( ^Z - - ^М + ) 2 D X N E l ( t x ( ^Z ^ ) )

By expanding and we have

Step -4 Extract the EEG Brain signals say Test database

Step -6 Find the PDFs of the Test data.

Step -7 Compare the Test data with the Train database and identify which emotion data does the EEG matches with the existing dataset.

Step -8 Displays the Emotion

=^alk Mkl+

f ( Zm el)-f (Zl e1)

M 21 I I 2l\ " ( "к^ak ^-ak^Mk^k )

VI. E xperimentation and R esults

We have considered 50 subjects for training and 25 subjects for testing purpose, emotions namely angry, sad, happy and neutral are considered for experimentation. A basic block diagram to analyze an EEG signal is shown in figure 4.

l 2 l ' k°k

" ZMfk ( Zm , e ^l ) - ZLfk ( Zl e¹ )' fk ( zm , e ) - fk ( zl e¹ )

^{- 2} Mk

"

^a k^k

-¹ ст ²¹ kk

f (Zm ,e)-f (Zl e1) f (Zm el)-f (Zl e1)

^l +i ) _}

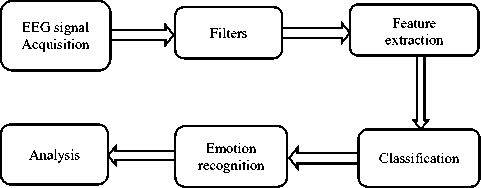
Fig.4. Basic block diagram to analyze the EEG signals

V. P roposed S ystem

After acquiring the brain signals, the frequency of each of the signals is identified [5]. A 10-20 electrode system was considered for experimentation. Each subject is first trained about the system and a test acquisition is conducted; after he / she get acquainted with the system, the actual readings generated and the frequencies generated are noted. The electrodes positions Fp1, FpZ, Fp2, F7, F3, F2, F4 and F8 electrodes are considered. This electrode position denotes the frontal positions and the emotions can be well interpreted from these potions. These frequencies are trained using DT-GMM. The process to be followed for the identification of the emotions is presented in algorithm in section A.

A. Algorithm for acquisition of brain signals using EEG

The steps to the followed for the acquisition of brain signals are given:

Step -1 Train the database

Step -3 Find the Probability Density function of each and every emotional dataset

B. Methodology of interpreting the brain signals based on Truncated Gaussian Mixture Model for mobilized and immobilized people

In order to record the brain signals, a scalp is fixed on the brain recorded EEG the neuronal electrical activity is recorded non-invasively, typically using small metal plate electrodes. The recordings are done using reference electrode(s) or bipolar linkages; the number of the electrodes will be changes used from application to application, the electrodes are typically placed at specific scalp locations. The voltages, are of the order of microvolt's (µV), reading should be carefully recorded to avoid interference and digitized so that it can be stored and viewed on a computer.

The general frame work of an EEG acquisition model is presented in figure 5.

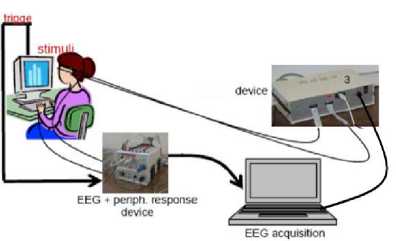
Fig.5. Hardware setup for signal acquisition

Prior to acquisition process, the electrodes will be in red color and when the electrodes are connected to the scalp using electro gel, these electrodes change their

color to green; and if the connectivity is not established properly, it can be visible in a color other than green, generally grey. The typical framework is shown in figure 6.

Fig.6. Participant wearing the EEG cap with 64 electrodes plugged

The basic EGG recording system consists of electrodes with conductive media, amplifiers with filters, an analog-to-digital (A/D) converter and finally a recording device to store the data. Electrodes, in conjunction with the electrode gel, sense the signal from the scalp surface; amplifiers bring the microvolt and often nano volt signals into a range where they can be digitized accurately; and the A/D converter changes signals from analog to digital form that can be finally stored or viewed on a computer. The various electrodes used and their locations are presented in following figure 7.

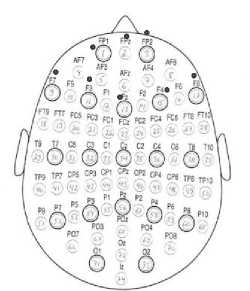
Fig.7. Top head view with the positions and names of the 64 electrodes used for EEG recording

For experimentation, eight electrodes configuration, only the BLUE electrodes were used. The electrode is placed with different positions such as 10-10 electrodes system, 10-20 electrode systems, 10-5 electrode systems according to the application. Dataset used for testing is SEED dataset and DEAP dataset. The experimentation with DT-GMM is carried out for immobilized persons and the results are tabulated in figure (8):

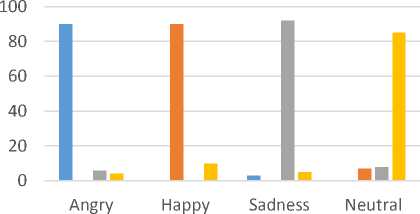
■ Recognition Emotion (%)/proposed model Angry

• ■    Recognition Emotion (%)/proposed model Happy

• ■    Recognition Emotion (%)/proposed model Sadness

• ■    Recognition Emotion (%)/proposed model Neutral

Fig.8. Recognition Rate (%) of Emotions in the case of immobilized persons Doubly Truncated Gaussian Mixture Model

Table 1 shows the results of the proposed classifiers when Electroencephalography (EEG) signals are used.

Table 1. emotion recognition rates

Name of the classifier	Double Truncated Gaussian Mixture Model
Data acquisition method: Electroencephalography	Happy	Sad	Angry	Neutral
	88	85	90	80

• VII. C onclusion

The emotion recognition system develops using Double Truncated Gaussian mixture model with the parameter of the distribution is updated using EM Algorithm. Using this updated equations, the Probability Density Function are estimated. Basing on the Maximum Likelihood Function the emotions are identified. The results of the proposed system surpassed the results of conventional models. The proposed method can further be enhanced if speech signal is also added for emotion recognition.