A Novel Circular Mapping Technique for Spectral Classification of Exons and Introns in Human DNA Sequences

Published Online March 2014 in MECS

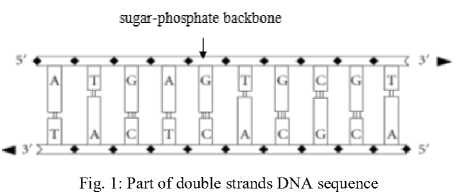
A single strand of DNA is a biomolecule consisting of many linked, smaller components called nucleotides. Each nucleotide is one of four possible types designated by the letters A, T, C, and G. The order of these bases in a gene determines the genetic variation, living, habits and nature of species. Moreover, DNA sequence has two distinct ends, the 5′ end and the 3′ end; as shown in Fig. 1. The 5′ end of a nucleotide is linked to the 3′ end of another nucleotide by a strong chemical bond, thus forming a long, one- dimensional chain (backbone) of a specific directionality ^[1]. Fig. 1 illustrates part of the DNA double strand DNA sequence.

A protein is also a biomolecule consisting of many linked, smaller components called amino acids. There are 20 possible types of amino acids in proteins and, just as the case in DNA single strands; they are connected with strong bonds, one after the other forming a long one-dimensional chain (backbone) of a specific directionality. Protein synthesis is governed by the genetic code which maps each of the 64 possible triplets (codons) of DNA characters into one of the 20 possible amino acids (or into a punctuation mark, like a stop codon, signaling termination of protein synthesis). As shown in Table 1, the 20 amino acids are indicated by both their one-letter and three-letters symbols. The codon ATG, serves as the START codon and it also codes for the M (methionine) amino acid; where methionine appears as the first amino acid of proteins, but it may also appear in other locations. The complete set of the 20 amino acids and the terminator codons (indicated by serial number 0 in the first row) are included in Table 2. It should be noticed that the first row (shaded row) in this table is not coded as amino acid, but it is a gene end terminator. Also, the thirteenth row (shaded row) represents the ATG amino acid or a gene start.

The DNA contains chromosomes that are blend of genic and intergenic regions as shown in figure 2. The exonic regions exhibit period three property that is not found in intergenic regions. This periodicity is a result of repeated identical nucleotides in identical triplet (codon) positions in these regions. This can be indicated by considering the periodic sequence C - - C - - C - - C - - …, where the blanks ‘-’ can be filled randomly by any one of the four bases A, T, C or G. This sequence gives a periodicity of three due to the repetition of base C at position 1 in each codon. Due to this property of exons, protein coding regions can be predicted and this helps in better identification of these regions. In fact the genetic information is stored in DNA as symbolic sequence. If we properly map a character string into one or more numerical sequences, then DSP provides a set of tools for solving problems in genomic field and reflect the biological properties in a numerical domain which helps to detect three periodicity regions in DNA sequence.

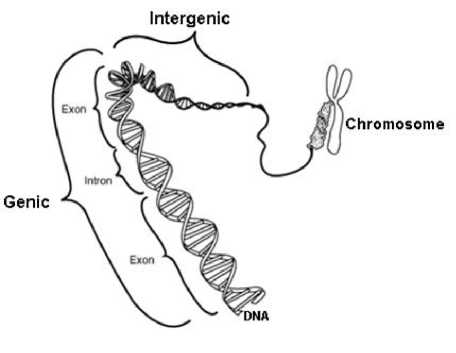
Fig. 2: Eukaryotic DNA consists of genic and intergenic regions

Table 1: Genetic code

Second position in codon

T

C

A

G

TTT

Phe

[F]

TCT

Ser

[S]

TAT

Tyr

[Y]

TGT

Cys

[C]

T

T

TTC

Phe

[F]

TCC

Ser

[S]

TAC

Tyr

[Y]

TGC

Cys

[C]

C

TTA

Leu

[L]

TCA

Ser

[S]

TAA

Ter

[stop]

TGA

Ter

[stop]

A

TTG

Leu

[L]

TCG

Ser

[S]

TAG

Ter

[stop]

TGG

Trp

[W]

G

CTT

Leu

[L]

CCT

Pro

[P]

CAT

His

[H]

CGT

Arg

[R]

T

й о "О о о б й .о о Рч

C

CTC CTA

Leu Leu

[L] [L]

CCC CCA

Pro Pro

[P] [P]

CAC CAA

His Gln

[H] [Q]

CGC CGA

Arg Arg

[R] [R]

C A

й "8 о о ,й й .о о Рч ^ н

CTG

Leu

[L]

CCG

Pro

[P]

CAG

Gln

[Q]

CGG

Arg

[R]

G

ATT

Ile

[I]

ACT

Thr

[T]

AAT

Asn

[N]

AGT

Ser

[S]

T

A

ATC

Ile

[I]

ACC

Thr

[T]

AAC

Asn

[N]

AGC

Ser

[S]

C

ATA

Ile

[I]

ACA

Thr

[T]

AAA

Lys

[K]

AGA

Arg

[R]

A

ATG

Met

[M]

ACG

Thr

[T]

AAG

Lys

[K]

AGG

Arg

[R]

G

GTT

Val

[V]

GCT

Ala

[A]

GAT

Asp

[D]

GGT

Gly

[G]

T

G

GTC

Val

[V]

GCC

Ala

[A]

GAC

Asp

[D]

GGC

Gly

[G]

C

GTA

Val

[V]

GCA

Ala

[A]

GAA

Glu

[E]

GGA

Gly

[G]

A

GTG

Val

[V]

GCG

Ala

[A]

GAG

Glu

[E]

GGG

Gly

[G]

G

The paper is organized as follows. Section I presents this introduction. Section II introduces the existing numerical representation methods of DNA sequences which are broadly classified into two major groups:

Fixed Mapping (FM) techniques and Physico-Chemical Property Based Mapping (PCPBM) techniques. Section III introduces the main applications of the existing numerical representation methods. Section IV introduces a new develop method called Circular Mapping to overcome the drawbacks of the existing methods for representing the nucleotide, where position of each nucleotide is taken in consideration. Sections V and VI describe the results and discussion of using CM for exons and introns classification in genomic sequences as compared with the existing methods. Finally, section VII concludes the paper.

Table 2: Codons and amino acids symbols

Serial number	Codons representation	Amino acid long name	Amino acid short name	Symbol
0	TAA, TAG, TGA	Terminator	Ter	[end]
1	TTT, TTC	Phenylalanine	Phe	[F]
2	TTA, TTG, CTT, CTC, CTA, CTG	Leucine	Leu	[L]
3	TCT, TCC, TCA, TCG, AGT, AGC	Serine	Ser	[S]
4	TAT, TAC	Tyrosine	Tyr	[Y]
5	TGT, TGC	Cysteine	Cys	[C]
6	TGG	Tryptophan	Trp	[W]
7	CCT, CCC, CCA, CCG	Proline	Pro	[P]
8	CAT, CAC	Histidine	His	[H]
9	CAA, CAG	Glutamine	Gln	[Q]
10	CGT, CGC, CGA, CGG, AGA, AGG	Arginine	Arg	[R]
11	ATT, ATC, ATA	Isoleucine	Ile	[I]
12	ATG	Methionine	Met	[M]
13	ACT, ACC, ACA, ACG	Thereonine	Thr	[T]
14	AAT, AAC	Asparagine	Asn	[N]
15	AAA, AAG	Lysine	Lys	[K]
16	GTT, GTC, GTA, GTG	Valine	Val	[V]
17	GCT, GCC, GCA, GCG	Alanine	Ala	[A]
18	GAT, GAC	Aspartic acid	Asp	[D]
19	GAA, GAG	Glutamic Acid	Glu	[E]
20	GGT, GGC, GGA, GGG	Glycine	Gly	[G]

• II.    Existing Mapping Techniques of DNA Sequence

• 2.1    Fixed Mapping Techniques

In literature [1] – [15], many different approaches have been proposed to address gene prediction as well as exons and introns classification problems. Existing numerical representation methods of DNA sequences can be broadly classified into two major groups: FM techniques [4] – [10] and PCPBM techniques [1], [11] – [15]

In FM techniques, the nucleotides of DNA data are transformed into a series of arbitrary numerical sequences. In general FM techniques include;

• • Voss representation technique ^[5]: It is an efficient method in detecting the coding and non-coding regions in a DNA sequences. Where, it maps the nucleotides A, C, T, and G into the four binary indicator sequences x_A(n) , x _c(n) ,  x _G(n) , and

xT(n)showing the presence (e.g., 1) or absence (e.g., 0) of the respective nucleotides as shown in the following example.

DNA Sequence :	…… T	T	G	T	C	A	C	T	C	G	G…
xл00 :	…… 0	0	0	0	0	1	0	0	0	0	0 …
x c 00 :	…… 0	0	0	0	1	0	1	0	1	0	0 …
x G 00 :	…… 0	0	1	0	0	0	0	0	0	1	1 …
xt (n) :	…… 1	1	0	1	0	0	0	1	0	0	0 …

• Tetrahedron representation technique [6]: It reduces         Voss mapping) to three in a manner symmetric to all the number of indicator sequences from four (i.e.         four components. In this method the four sequences

х_д(n), х c (n), x c (n), and x_T(n) are mapped to four 3- dimensional vectors pointing from the center to the vertices of a regular tetrahedron. Thus, the final tetrahedral sequences are calculated from (1) – (3).

The Voss and tetrahedron representations are equivalent representations for the purpose of power spectrum computation, but obtaining DNA spectrograms of bimolecular sequences is the main application of this method.

xr(n) = — (2xT(n) - xc(n) - x6(n))

• x, (n) = ^(xcW-xtO.))

,, 1,.......

xb(n) = 3 (3xA(n) - XT()) - xc(n)^

• - x gOO)

• •    Complex representation technique [6]: It reduces the dimensionality of the tetrahedral representation to two by projecting the basic tetrahedron on a complex plane. It reflects the complementary nature of A-T and C- G pairs as A= 1 + j , C = - 1 + j , G = - 1 - j , and T = 1 - j.

• •    Integer representation technique [7]: It is a onedimensional (1-D) mapping of the DNA bases which can be obtained by mapping numerals {0, 1, 2, 3} to the four nucleotides as: T=0, C=1, A=2, and G=3. This method has some mathematical properties which does not exist in a base sequence. Hence its DSP applications are limited suggesting that these integer mappings need to be used carefully for a given application.

• •    Real number technique [8]: It represents A by -1.5, T by 1.5, C by 0.5, and G by -0.5. The assignment of a real number to each of the four bases does not necessarily reflect the structure present in a DNA sequence. In the computation of correlations, real representations are preferred over complex representations.

• •    Quaternion technique [9]: It assigns pure quaternions to each base: A= i + j + к, C= i - j - к, G= -i - j + к , and T= -i + j - к . This method of mapping can be used to compute the 3-periodicity in DNA sequences. It has been often observed that the occurrence of repetitive structures (or tandem repeats) in genomic data is symptomatic of biological phenomena. Perhaps the best known example of this association is the 3-base repetition of codons, which is characteristic of protein coding regions in DNA sequences of eukaryotic cells.

• •    Inter-nucleotide distance technique [10]: It represents each DNA nucleotide (i.e., A, C, G, or T) with a number representing the distance between the current nucleotide and the next similar nucleotide. While scanning the sequence from left to right, if a similar

• 2.2 Physico Chemical Property Based Mapping Techniques

nucleotide is not found, the sequence value of the current nucleotide is the length of the remaining sequence. For example, for the DNA sequence x[n] = AGTTCTACCGAGC, the inter-nucleotide distance sequence would be:

ind [n] = {6,8, 1, 2, 3,7,4,1,4,2, 2, 1,0}.

In PCPBM techniques, biophysical and biochemical properties of DNA biomolecules are used for DNA sequence mapping [4]. So they can be used in searching for biological principles and structures in biomolecules. In general these techniques include:

• •    Electron-Ion Interaction Potential (EIIP) mapping techniqu e [11]: It represents the distribution of the free electrons’ energies along the DNA sequence. EIIP indicator sequence is formed by substituting the EIIP of the nucleotides A=0.1260, C=0.1340, G=0.0806, and T=0.1335 in a DNA sequence. This method may be used as a coding measure to detect probable coding regions in DNA sequences.

• •    Atomic number mapping technique [12]: In this method a single atomic number indicator sequence is formed by assigning the atomic number in each nucleotide as: A=70, C=58, G=78 and T=66 in a DNA sequence. Its DSP applications are also limited as integer representation.

• •    Paired numeric mapping technique [1]: In this technique nucleotides (A-T, C-G) are to be paired in a complementary manner and values of +1 and -1 are to be used respectively to denote A-T and C-G nucleotide pairs. This representation incorporates a very useful DNA structural property, in addition to reducing complexity.

• •    DNA walk mapping technique [13]: It is a graphical representation of DNA sequences that helps to study the scale-invariant long-range correlations of a DNA sequence, a step is taken upwards (+1) if the nucleotide is pyrimidine (C or T) or downwards (-1) if it is purine (A or G). The DNA walk allows one to visualize directly the fluctuations of the purine -pyrimidine content in DNA sequences. It is providing long range correlation information; sequence periodicities; changes in nucleotide composition; offering numerical and graphical visualization.

• •    Z-curve mapping technique [14]: It is a 3-D curve that provides a unique representation for visualization and analysis of a DNA sequence. This representation has been also employed for gene identification and DNA protein coding measure. It converts the DNA sequence into an equivalent three dimensional representation based on the symmetry of the regular tetrahedrons. In order to generate Z-curve sequences, the DNA sequence is first converted into four binary

  indicator sequences Хд (n), х_с (n), X_G (n ) , and Xy (n) by Voss mapping, then the cumulative numbers of the DNA bases for n samples are then calculated using:

  
  

  I

  
  

  ⁼

  
  

  n

  ∑ Xl [ i ],

  1=0

  
  

  I ∈ { A , C , G , T }

  
  
  
  

  analysis of DNA sequences using wavelet based time series approach for extracting statistical information from DNA sequences. The extracted information contains the variance information of amino/keto, purine/pyrimidine and weak/strong hydrogen bond distribution in a DNA sequence.

  
  

The four cumulative sequences A n,Cn, Gn, and T are in turn used to define three Z-curve sequences x n,yn , and z n as follow s [15]:

xn = 2[^n - ^n-1 + ^n - ^n-1]-1,

Уп = 2[^n - ^n-1 + Cn - Cn-1]-1,

Zn =2[ ■^n -     + ^n - ^n-1]-1.

• III.    Gene Prediction using Existing Mapping Techniques

Gene prediction which refers to locating the proteincoding regions (exons) of genes in a long DNA sequence is the main problem in genomic field. Many different approaches [16] ^- [20] have been developed to address this open problem but still a better optimized solution is essential. Kakumani and Devabhaktuni [16], presented a model-based exon detection approach using statistically optimal null filter. In [15] a model of the period-3 characteristic is employed to maximize signal-to-noise ratio, using least-squares optimization criteria to rapidly detect the presence of exons in DNA sequences. Akhtar et al^. [17], investigated the effect of window length on selected signal processing-based gene and exon prediction methods. They optimize these methods to improve the prediction accuracy by employing the best DNA representation, selecting a suitable window length, and boosting the output signals to enhance protein coding and suppress non-coding regions. Hota and Srivastavan [18] observed that complex indicator sequence provides strong spectral component compared to EIIP indicator sequence. They also observed that windowed Discrete Fourier Transform (DFT) considering complex indicator sequence provides better exon prediction compared to windowed DFT considering EIIP indicator sequence and digital filters methods. Computational overhead is reduced by 75% in complex indicator sequence compared to binary indicator sequence. Grandhi and Kumar [19], proposed a new lower dimensional mapping ( 2-simplex mapping method ) by assigning the nucleotides to the three corners and one center of a triangle which reduces the computational complexity by half, producing results nearly equal to those produced by a higher dimensional mapping. Gupta et al. [20], presented a novel and generic approach for the

• IV.    Proposed Circular Mapping Approach

In this section a new numerical representation technique for DNA sequence is introduced. In this technique each nucleotide (A, T, C, or G) is represented by a complex numerical value according to nucleotide’s type and its position in codons along the DNA sequence. All values that represent nucleotides are located on circle so that a Circular Mapping of the bases is obtained. This method has many applications but exons and introns classification problem is only considered here. The efficiency of this method in exons and introns classification depends on the correct choice of an angle (θ) between the three positions of nucleotides in codon and the correct arrangement of the four nucleotides around space as will be explained in details in the following paragraphs. All codons are represented on a circle with radius “r”. Although “r” can be any value, it will be considered here one for simplicity.

The space of the circle is divided into four regions; one quarter for each nucleotide. For example, the A, C, G, and T nucleotides are placed in the first, second, third and fourth quadrants respectively as shown in Fig. 3. In fact, this is one possible choice and other arrangements can be adopted by placing the four nucleotides in different quadrants. It should be noticed that, the nucleotides arrangement is the first parameter that affects the precision of exons and introns classification. After selecting the prober arrangement, each nucleotide is placed in one of the three possible positions inside the corresponding quadrant. Thus a total of 12 positions, three for each one of the four nucleotides (A, T, C, or G) are possible. For example, nucleotide “A” (it may be any other nucleotide depending on chosen arrangement) has the three possible positions separated by angle “θ” as shown in figure 4. Where the nucleotide “A” is located in the first position if the codon starts by “A”, in the third position if the codon ends by “A” and is located in the second position if it is in the middle of the codon. The angle (θ) is the second parameter that affects the precision of exons and introns classification. To facilitate understanding the CM method, an example of one codon (three nucleotides) is considered, the positions of the four nucleotides inside the four quarters for the codon “CAT” is shown in figure 5.

Referring to figure 5 it can be deduced that, the three positions only represent each codon on circle and the complex numerical values that represent the four nucleotides can be determined from the following equations.

A(m) = г {cos(^ - 9 + f) + i sin(^ - 9 + f}    (8)

C( m) = r {c ss(^ -9 )+f ) + i s in(^ - 9 + f] (9)

G( m) = r {cos(^ -9)+f ) + i s tn^ - 9) +

f )

T(m) = r {co s(y -9)+f) + i si n(y - 9) + f} (11)

Where, f = (m - 1) 9;

• "m" = 1, 2, 3 denotes the first, second, and third positions in codon;

• "9" is the angle between the vector directed from the circle origin to the second position and the two other vectors directed from the origin to the first and third positions of nucleotides in codon as shown in figure 4; and

• " r" is the radius of the circle (assumed constant value).

  

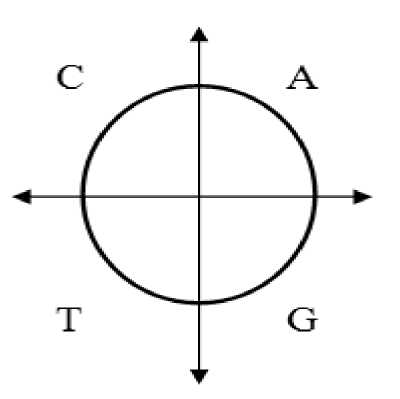
Fig. 3: Nucleotide placement on circle space

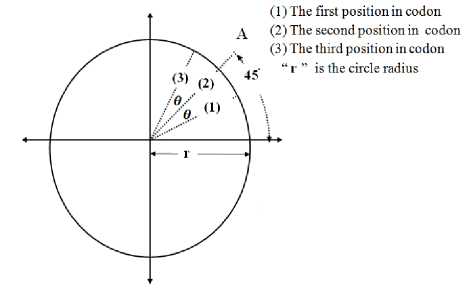
Fig. 4: The three possible positions of nucleotide “A” inside the first quadrant

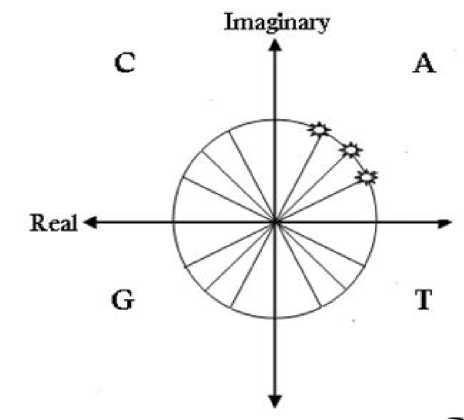
Fig. 5: Circular representation of the “AAA” codon

Representing any nucleotide by this method requires knowing the type of the nucleotide (A, T, C, or G) and its position inside the codon. The type of the nucleotide determines which quadrant the nucleotide belongs to and the choice of one of the three positions inside quadrants depends on the position of the nucleotide inside the codon. The same is applied to all nucleotides in the DNA sequence and the final numerical sequence can be used in exons and intron classification.

Table 3: The all possible 12 arrangements and their equivalents ( Qi denotes the ith Quadrant )

Arrangement number	Arrangement	Possible positions				Equivalent arrangement
		Q 1	Q 2	Q 3	Q 4
1	ACTG	A	C	T	G	TGAC
2	ACGT	A	C	G	T	GTAC
3	AGCT	A	G	C	T	CTAG
4	AGTC	A	G	T	C	TCAG
5	ATGC	A	T	G	C	GCAT
6	ATCG	A	T	C	G	CGAT
7	CATG	C	A	T	G	TGCA
8	CAGT	C	A	G	T	GTCA
9	CGTA	C	G	T	A	TACG
10	CTGA	C	T	G	A	GACT
11	TAGC	T	A	G	C	GCTA
12	TCGA	T	C	G	A	GATC

The best choice of the angle (9) and the selection of the proper arrangement of nucleotides for the circular mapping numerical representation are the most important parameters that have great effects on the precision of exons and introns classification. For the four quadrants and the three possible positions of the nucleotides, 24 possible arrangements exit as illustrated in Table 3. From (8) – (11), it should be noted that when the nucleotide position is rotated by 1800 (i.e., when a certain nucleotide rotated from the first, second, third, and fourth positions to third, fourth, first, second positions respectively) the same numerical mapping results. For example, the AGTC arrangement has the same numerical mapping as the TCAG arrangement. As a result, for each arrangement there exists an equivalent arrangement as shown in the last column of Table 3. So, the number of possible arrangements is reduced from 24 to 12 arrangements. In addition to the selection of the prober arrangement, the angle (θ) also has an effect on the exons and introns classification; where 0 < θ < 450.

• V.    Results and Discussions

To investigate the efficiency of the CM technique in exons and introns classification, the dependence of classification accuracy on the nucleotides arrangements and the value of the angle θ have been investigated. For this propose, θ is varied from 1o to 44o with 1o step and all the twelve possible arrangements are considered. As a result, 528 possible θ values will be considered. Moreover, the period-3 property for the DNA sequences has been adopted.

The period-3 property of the L- length DNA sequence implies that the discrete Fourier transform (DFT) coefficients corresponding to frequency L/3 is large. This property is related to the different statistical distributions of codons between protein-coding and non-coding DNA sections. So, 3-periodicty is used as a basis for identifying the coding and non-coding regions. The considered DNA sequence is first converted to numerical values using the proposed CM technique and then discrete Fourier transform (DFT) based approach is adopted to extract the period-3 value of DNA sequences. The finite-length DFT sequence, X[k] for k = 1 to N for a numerically represented DNA sequence x(n) for n =1 to N is defined by [21].

N

X [ к ]= ¹ ∑ x ( n ) W, ^{( и} )(  ⁾,

√

- ;2тг for 1≤к≤ N and И/jv =

Using the windowing approach with a rectangular window length of L bases and an overlap width of L-3 bases between two adjacent windows, the normalized sum (X т [k] ) of the DFT spectrum (X m[k]) of each of the windowed sequences (x m (n) for m = 1 to N ) gives

Nw

X_T [ к ]= ¹∑ ^m [ к ]          (13)

m=l

Where, N is the number of shifted windows. The spectral content measure can be obtained by calculating the power spectrum of (13) as

s[ к ] = | X_T [ к ]|²                    (14)

The period-3 spectral component (P3 ) can be obtained from the power spectral content measure of a numerically represented sequence as p, =[N⁄3 +1]               (15)

The statistics of the period-3 values determined from a training set of exon sequences and intron sequences can be used to classify an untrained sequence to be either an exon sequence or an intron sequence. For this purpose let meanPBe and sdPBe represent respectively the mean and standard deviation of the period-3 values obtained from the exon sequences of a training set; and meanP3 j and sdP3 j represent respectively the mean and standard deviation of the period-3 values obtained from the intron sequences of the same training set. Consequently, the threshold value for classification is defined as [21].

T3

sdP_3e ∗ meanP_3i + sdP_3i ∗ meanP_3e sdP_3e + sdP_3i

Using (16), if a test sequence has a period-3 value P3t greater than or equal toTз , the test sequence is classified as an exon sequence; otherwise it is classified as an intron sequence. Here the circular mapping is adopted for exons and introns classifications. The exons classification (EXCLASS), introns classification (INCLASS) and the precision value are evaluated by the following three equations [22];

EXCLASS

NCEC

:---------------------------------------------------------------

Exon number

100 %

INCLASS =          ×100 %

Intron number

_   . . NCEC+ NCIC лzi rw

Precision =          × 100%

TEIN

Where, NCEC, NCIC and TEIN are the number of correct exons and the number of correct introns classifications and the total number of exons and introns respectively.

Equations (13) - (19) are applied to training and testing sequences downloaded from USCS Assembly database: Feb. 2009 (GRCh37/hg19) (Clade: Mammal, Genome: Human, Assembly: Feb.2009 (GRCh37/hg19), Group: Genes and Gene rediction Tracks, Track: UCSC Genes, Table: knownGene) [23] – ^[26]. Sequences that are used for training and testing to determine the best angle and arrangement are consisted of a total of 4000 Exon sequences; sequences 1 to 3000 are used for training and sequences 3001 to 4000 are used for testing; and a total of 4000 Intron sequences; sequences 1 to 3000 are used for training and sequences 3001 to 4000 are used

A Novel Circular Mapping Technique for

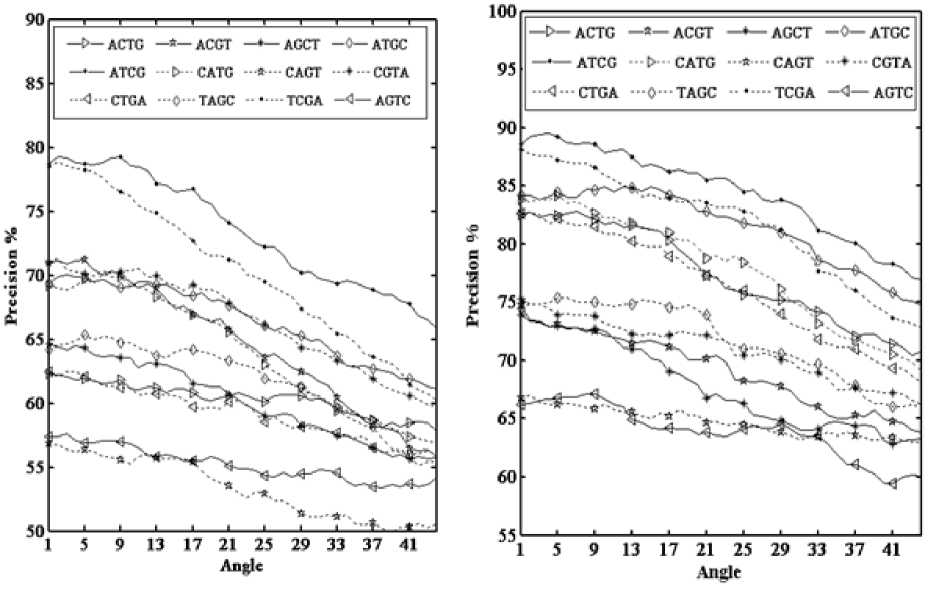
Spectral Classification of Exons and Introns in Human DNA Sequences for testing. Figure 6(a) and figure 6(b) show the precision of the twelve arrangements at 44 different angles with a window length of 15 bases and an overlap window length of 12 bases for DNA sequences with lengths 100 and 500 base pairs (bp). For best exon and intron recognition, the precision should be maximized by varying the angle (θ) for certain arrangement. For the ATCG arrangement, the maximum precision has been obtained at the angle (θop = 0.267o). This value has been determined using the Matlab optimization tool box. The resulting CM numerical representations for A, T, C, and G nucleotides are obtained from (1) – (4) with θ =0.267o and arrangement ATCG; as illustrated in Table 4. These values will be adopted in exon and intron recognition in the following section.

Table 4: The nucleotide values for circular mapping (α1, α 2, α3 denotes first, second, and third position in codon, α =A, C, G, or T.

Nucleotide ( α )	Values of nucleotide in numerical sequence
	Value of nucleotide in the first position in codon (α1)	Value of nucleotide in the second position in codon (α2)	Value of nucleotide in the third position in codon (α3)
A	0.7104 + 0.7038i	0.7071 + 0.7071i	0.7038 + 0.7104i
T	-0.7104 + 0.7038i	-0.7071 + 0.7071i	-0.7038 + 0.7104i
C	-0.7104 - 0.7038i	-0.7071 - 0.7071i	-0.7038 - 0.7104i
G	0.7104 - 0.7038i	0.7071 - 0.7071i	0.7038 - 0.7104i

(a)

(b)

Fig. 6: The precision of a DNA sequence with different sequence lengths. (a) 100 base pairs sequence length and (b) 500 base pairs sequence length

• VI.    Comparison between the Proposed CM Technique and the Existing Techniques

In this section seven existing DNA numerical representation techniques are compared with the proposed CM method [1], [6] - [8], [11] - [13]. The comparison is based on the period-3 property for the purpose of exons and introns classification. This has been carried out by applying (18) - (19) on training and testing sequences with different intron and exon lengths range from minimum length 50bp to maximum length 500bp. The base sequences are downloaded from USCS Assembly [23] - [26]. The sequences that are used for training and testing consist of 4000 sequence for each exon and inron sequences. By using 10-fold crossvalidation the data is first partitioned into 10 equally sized segments or folds (each group consist of 400 sequences). Subsequently 10 iterations of training and validation are performed such that within each iteration a different fold of the data is held-out for validation, while the remaining “9” folds are used for training. . The precision defined by (19) has been used as a performance measure. The final results of measuring classification performances of all the seven existing numerical representation and the proposed method are summarized in Table 5. Window length of 15 bases and an overlap window length of 12 bases are used to obtain these results.

Table 5: Exons and introns classification performance by different methods

Method	Representation	Precision (%) when using 10-fold cross validation										Average
		F1	F2	F3	F4	F5	F6	F7	F8	F9	F10
Intege r [7]	A=2, C=1, G=3, T=0	66.1	86.5	74.1	82.5	80.9	90.3	75.8	76.6	75.9	92.6	80.1
	A=0, C=1, G=3, T=2	72.9	84.4	71	74.1	79.5	91.9	76.6	79.9	77.4	91.1	79.9
Real [8]	A = -1.5, C = 0.5, G = -0.5, T = 1.5	62.1	75.6	58.8	70.6	78.9	83.5	79.8	75.3	65.1	97.8	74.7
Complex [6]	A =1+ j, C = -1+ j, G = -1- j, T = 1 - j	74.6	85.4	82	82.1	89.5	91.1	78	81.3	84.8	98	84.7
EII P [11]	A=0.1260, C=0.1340, G=0.0806, T=0.1335	72.3	81.9	75.4	72.8	84	93.5	81.9	85.9	80.3	96.1	82.4
Atomic numbe r [12]	A=70, C=58, G=78, T=66	67.5	73.4	69	70.5	75.5	79.6	73.4	73.4	59.5	93.4	73.5
Paired Numeric [1]	A or T = 1, C or G = -1	77.5	88.4	80.6	84.4	92.1	95.3	84.3	82	91.5	97.6	87.4
DNA wal k [13]	C or T = 1, Aor G = -1	62.5	76	63.9	75	79.1	82.8	79.3	73.5	62.9	97.8	75.3
Proposed CM	A, C, T and G are evaluated using (8) – (11).	80.6	90.4	81.4	85.3	93.8	91.9	89.5	81.8	87	98.4	88

• VII.    Conclusion

A novel CM method for exons and introns classification is introduced in this paper. It is a graphical representation for DNA sequence that maps each nucleotide by a complex numerical value depending not only on type but also on its position in codons. Therefore, it overcomes the drawbacks of the existing mapping methods. The proposed approach showed significant improvement in exons and introns classification as compared with the existing techniques.

The efficiency of this method in exons and introns classification depends on the right choice of angle (θ) between the vector directed from the circle origin to the second position and the two other vectors directed from the origin to the first and third positions of nucleotides in codon and also depends on the chosen arrangement of the four nucleotides around space as indicated by results from the power spectral analysis over human genome download from USCS Assembly: Feb. 2009 (GRCh37/hg19). The analysis revealed that ATCG arrangement gives the highest precision compared with other methods.