A Novel Distance Metric for Aligning Multiple Sequences Using DNA Hybridization Process
Автор: Jayapriya J, Michael Arock
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 6 vol.8, 2016 года.
Бесплатный доступ
This paper elucidates a new approach for aligning multiple sequences using DNA operations. A new distance measure using DNA hybridization melting temperature that gives approximate solutions for the multiple sequence alignment (MSA) problem is proposed. This paper provides proof for the proposed distance measure using the distance function properties. With this distance measure, a distance matrix is constructed that generates a guide tree for the alignment. Providing an accurate solution in less computational time is considered to be a challenging task for the MSA problem. Developing an algorithm for the MSA problem is essentially a trade-off between finding an accurate solution and that can be completed in less computational time. In order to reduce the time complexity, the Bio-inspired technique called the DNA computing is applied in calculating the distance between the sequences. The main application of this multiple sequence alignment (MSA) is to identify the sub-sequences for the functional study of the whole genome sequences. The detailed theoretical study of this approach is explained in this paper.
Multiple sequence alignment, DNA Hybridization, Sequence alignment, Distance matrix, DNA structure
Короткий адрес: https://sciup.org/15010830
IDR: 15010830
Текст научной статьи A Novel Distance Metric for Aligning Multiple Sequences Using DNA Hybridization Process
Multiple sequence alignment (MSA) is an important and challenging problem in Bio-informatics. These alignments are used for constructing profile and to cluster proteins, depending upon the sequences similarities. Proposing an efficient algorithm for the MSA problem with the accurate solution in less time is a key research topic in sequence analysis. In sequence analysis, aligning the sequence is the initial step. Aligning a sequence can be defined as finding column match for a set of sequences. Aligning two sequences are known as pair-wise alignment. The MSA is an extension of pair-wise alignment and can be defined as a process that finds the match along the columns among n sequences where n is the number of sequences and n>2. These alignments are shown in Figure 1.

Fig.1. Sequence Alignment
Finding the maximum similar residues between multiple sequences is given as SA=SS U {-}, where SA is the aligned sequences, SS is the sequence set with multiple sequences and ‘-‘ represents the gaps that are used to adjust the length of the sequences. There are two basic approaches like exhaustive and heuristic for the multiple sequence alignment problems. Exhaustive method handles all possible ways of sequence matching like Dynamic Programming (DP) sequence matching in pairwise alignment.
Basically, DP approach is good for aligning two sequences but for more sequences its complexity grows. The heuristic approach can be of three categories, namely the progressive type, iterative type and block-based type. The progressive alignment combines the most similar pair of sequences and continues with the distantly related one until all the sequences are aligned. Some of the most popular MSA program using progressive type alignment are ClustalW [1] used for medium length sequences, T-Coffee [2] used for distantly related sequence sets which is slower than ClustalW, and ProbCon [3] used especially for protein sequences. The second type is the iterative alignment that repeatedly aligns the initial sequences and adds the new sequences to the growing set. There are many programs based on iterative alignment like MAFFT [4] that incorporates different strategies like progressive and iterative methods. The third type is a local alignment based approach, used to find the conserved domains and motifs. The two most common web-based programs of block-based type are DIALIGN2 [5] and Match-Box [6].
Other efficient approaches are HHM [7], simulated annealing [8], evolutionary algorithms or Bio-inspired algorithms [9] for MSA problem. Finding the exact solution for all the biological issues are considered as NP-complete problems. Still, there is a need for an efficient algorithm considering both accuracy and computational time.
-
II. Related Work
For more than a decade, many algorithms have been proposed to solve the MSA problem. Other than these above-mentioned types the sequences are aligned by finding the distance between them. In general, distance can be defined as the number of variations found among the sequences. Fundamentally, some common distance measure like edit distance, Euclidian distance, Levenstein distance, Lempel-Ziv complexity [10] etc. are used for calculating the distance between sequences where each one has own merits and demerits. Jiang et al., [11] in 2002 proposed the notion of edit distance to measure the similarity between two RNA secondary and tertiary structures, by integrating various edit operations performed on both bases. Edgar et al., [12] in 2004 proposed a MUSCLE program that uses a two distance measure namely a k-mer distance (for an unaligned pair) and the Kimura distance (for an aligned pair).
In 2008, Eddy et al., [13] have proposed a probabilistic model of local sequence alignment that simplifies statistical significance estimation. In 2011, Zhang et al., [14] has proposed a new distance based on dinucleotide absolute frequency in large DNA sequences. In 2011, Xu Li and ZhenzhouJi [15] have proposed a parallel design for edit distance algorithm for DNA sequence alignment. Naznin et al., in 2011 [16] have proposed a Vertical Decomposition with Genetic Algorithm (VDGA) for MSA. In 2012, Garai et al., [17] have applied a new genetic approach for finding an optimized match between two DNA or protein sequences. Nguyen et al., [18] in 2013 have proposed Knowledge-based multiple sequence alignment (KBMSA) algorithms that utilize the existing knowledge databases. A common drawback of this algorithm is that it needs extra time for querying the databases.
In 2014, Sun et al., have developed [19] a new variant of PSO, called the random drift particle swarm optimization (RDPSO) algorithm, along with Hidden Markov Model (HMM) learning tasks in MSA problem. In 2014, Kaya et al., [20] have proposed multi-objective genetic algorithm with an affine gap for MSA problem. In Micha Modzelewski et al in 2014 [21] have proposed a new graph-clustering based algorithm for aligning sequences. The main disadvantage of this work is its high computational complexity.
In 2014, Arabi E. keshk [22] has proposed an enhancement of dynamic algorithm of genome sequence alignment, which called EDAGSA. This modification depends on ignoring the unused data of the comparison matrix and evaluates the only three main diagonals of that matrix. In 2015, Bodenhofer et al., [23] developed an R package for multiple sequence alignment. Jayapriya et al., in 2015 [24] proposed a parallel approach using Grey Wolf Optimizer technique for sequence alignment problem.
From the earlier different perceptions of the study, it is concluded that the above said approaches and distance measure are time-consuming ones. To overcome this in this paper, we developed a novel distance measure using the melting temperature in the DNA hybridization process. DNA hybridization is the process in DNA computing, a Bio-inspired technique for solving the MSA problem. The main advantage of Bio-inspired algorithms than others is that they reduces the computational time. The DNA computing approaches are used to solve many biological problems owing to its vast parallelism and high-density storage. The main contribution of this paper is to provide a novel distance measure for aligning multiple sequences and prove the proposed measure using the distance function properties.
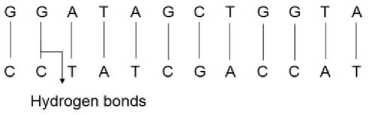
Fig.2. Structure of a DNA
-
A. Importance of MSA
The MSA has been chosen, as it reveals more biological information than the pair-wise alignment. Its applications are to identify and to represent the conserved features of DNA/protein sequences. It locates remotely homologous regions, motifs in protein families, disulfide bonds, and structural blocks like helices or sheets, construct a profile and to cluster proteins according to similar regions. These sub-sequences or patterns are also necessary for the study of the sequence's structure and functions. The important challenge in the MSA problem is to develop better methods for aligning larger data sets having both more and longer sequences in less computational time with accuracy.
The rest of the paper is organized as follows: Following the introduction and importance of MSA in above section, related work is given in Section II. The basics of DNA like DNA structure and its operations in Section III. The proof for proposed distance measure is given in Section IV. And in Section V, a theoretical approach of the proposed work is discussed. Eventually, Section VI concludes this paper.
-
III. Basics of Dna Computing
DNA computing can be defined as performs of computations using biological molecules, rather than traditional silicon chips. The main idea, that individual molecules (or even atoms) could be used for computation was presented in 1959 by American physicist Richard Feynman on nanotechnology.
The primary advantage offered by most proposed models of DNA based computation is the ability to handle millions of operations in parallel. The massively parallel processing capabilities of DNA computers may give them the potential to find tractable solutions to otherwise intractable problems, as well as potentially speeding up large, but otherwise solvable, polynomial time problems requiring relatively few operations. The ability to obtain tractable solutions to NP-complete and other hard computational problems has many implications to real life problems, particularly in business planning and management science. Many of the cost optimization problems faced by managers are in NP-complete and are currently solved using heuristic methods and other approximations. These problems include scheduling, routing, and optimal use of raw materials and correspond to problems already solved, either theoretically or experimentally, using DNA computation.
-
A. DNA structure & its operations
The genetic information of cellular organisms is encoded in Deoxyribonucleic acid (DNA). This consists of a polymer chain that is known as DNA strands. Each strand is viewed as a chain of nucleotides or bases. Adenine, Guanine, Cytosine, and Thymine are the four DNA nucleotides that are commonly abbreviated to A, G, C and T respectively. Two separate strands are bonded to form a double helix of DNA. Bonding occurs by the pairwise attraction of bases; A with T and G with C. A-T and G-C pairs are known as complementary base pairs. The base pairs are connected by hydrogen bonds. A hydrogen bond (HB) is a type of attractive interaction between an electronegative atom and a hydrogen atom bonded to another electronegative atom. The two strands of DNA are connected together by hydrogen bonds that occur between complementary nucleotide base pairs. The structure of a DNA is shown in Figure 2.
-
B. DNA operations
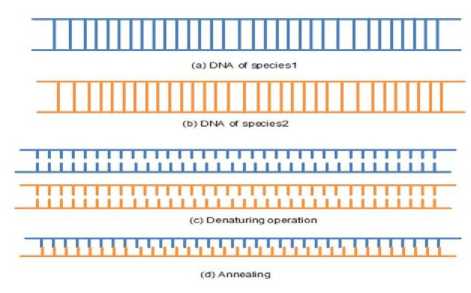
Fig.3. DNA Operations
The DNA hybridization is a process that has different operations like denaturing and annealing [24] in DNA computing. These operations are used in this work for distance calculation. Denaturing (melting) is an operation that breaks a double-stranded DNA into two single strands by heating it to a particular temperature. Basically, DNA strands are combined with their complementary base pairs. G-C pair is connected with three hydrogen bonds and A-T pair with two hydrogen bonds. From these bonding relationships, it is concluded that G-C pair take more energy than A-T pair. Depending upon the number of A-T and G-C base pairs in the sequence, the temperature required is defined. The next operation is the annealing, which joins two single DNA strands into a double strand DNA by the cooling process. If two species are close to each other then it has more hydrogen bonds between them and has less hydrogen bond when they differ. The DNA operations are shown in Figure 3.
-
IV. Proposed Work
To find the distance between the sequences, as a first step the double strand of two different species is denatured. Different temperatures, used in DNA operations are noted and their differences are given as distance measure to form a distance matrix. The following Algorithm 1 shows the approach to align multiple molecular sequences.
Algorithm 1
Input: Multiple Molecular Sequences set SS Output: Aligned Sequences SA
-
1. Lab process
-
a. Multiple sequences in a test tube
-
b. Allowed for DNA operations
-
c. Temperature variations are noted
-
2. Distance Matrix
-
a. Using the temperature variations Distance Matrix is formed
-
3. Construction of Guide tree by UPGMA method
-
4. Progressively sequences are aligned using Guide tree to obtain the final alignment.
Each and every step in the algorithm is explained in the following subsections.
-
A. Distance Calculation
The temperature applied for denaturing is noted as t 1 (s 1 ) and t 1 (s 2 ) for species1 (s 1 ) and species2 (s 2 ) respectively. In the next step, the two single strands DNA of different species are forced to bond with each other even they are unable to pair with its perfect base pairs. The last step is to denature the two different single strand bonding. Now the temperature is noted as t(hs) for the hybrid sequence (hs). When the hybrid DNA sequence is broken at minimum temperature, then it is concluded that the distance (difference) between them is high. This is because less hydrogen bond needs less temperature to split them. The distance measure of two species ∆T is calculated by finding the difference between the two temperatures. The following Figure 4 shows the overview of the alignment approach using a novel distance measure.
The equation (1) represents the difference of the species1 that is given in ∆T1.
A T 1 = t 1 ( s 1 ) - t(Ss) (1)
And in the equation (2), the difference of the species 2 is given in ∆T2.
AT = t(s) - ths) (2)
D(s, s) = max(AT, AT) (3)
where S is the set of sequences. D is the distance between species s1 and s2. In this equation, the maximum value among two temperatures ∆T 1 and ∆T2 of two species s1 and s2 are taken as the distance among them. The proposed distance measure is proved using the distance function properties. The steps to calculate the distance matrix in lab is shown in Figure 5.
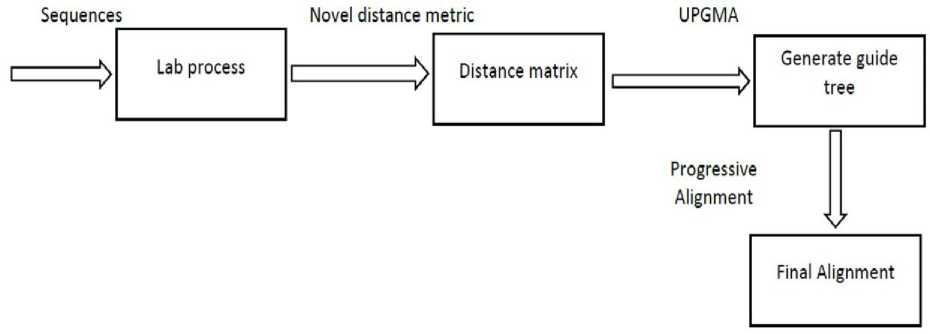
Fig.4. Overview of the Proposed Work
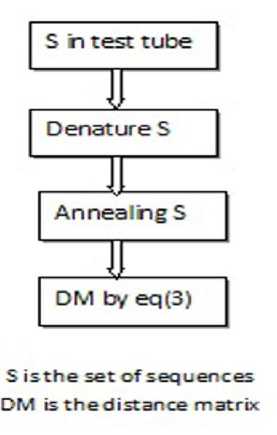
Fig.5. Steps to Calculate Distance Matrix
D ( x , x ) = 0 V x e X (6)
• Triangularity
D ( x , z ) < D ( x , y ) + D ( z , y ) V x , y , z e X (7)
In this proposed work, S is the sequence set same as X, x and y are sequences s x and s y respectively.
Theorem 1 The distance between two sequence s x and s y D(s x ,s y ) has the postiveness property.
Proof: When the two sequences are dissimilar there is no hydrogen bonds between them and it needs zero temperature for the denature process.
\ 0, if x , yareDsi ( noHB ) D ( x , y ) = <
[> 0, if x , yare si ( HB )
Distance function: Assuming X is a finite set of objects (bio-sequences), D is a distance function that should hold the following four properties [26]:
• Positiveness
D ( x , y ) > 0 V x , y e X (4)
• Symmetry
D ( x , y ) = D ( x , y ) V x , y e X (5)
-
• Reflexivity
where Dsi and si denote dissimilar, similar between sequence x and y respectively, HB is the hydrogen bond. From the above statement and the equation (8), it is concluded that the distance measure can have only positive values. Thus it is proved that the proposed distance measure holds the positiveness property.
Theorem 2 The distance between two sequences sx and s y , D(s x , s y ) has the symmetry property.
Proof The distance of the two sequences s 1 and s 2 is given in equation (3). To find the distance between sequences s 2 and s 1 , the same equation (3) is used. Because the same temperature is obtained among which the maximum is taken. And this can be given as equation (9).
D(s , s ) = max(A T , A T ) (9)
From the equation (3) and (9), it is concluded that the proposed distance measure satisfies the symmetry property of distance metric.
Theorem 3 The distance between two sequences s x and s y D(s x , s x ) has the reflexivity property.
Proof When the distance between the same sequences (s1) is calculated, it is equal to zero because when DNA operations are applied, the temperature used is same.
Here, the proof is as follows:
A T = ^ ( s ) - (Us) (10)
The equation (10) becomes zero as both t 1 (s 1 ); t(hs) values are same. Then D(s 1 ,s 1 )= 0. Thus it is proved that the proposed measure holds reflexivity property.
Theorem 4 The distance between two sequences s x and s y D(s x ,s y ) has the Triangularity property.
Proof Assuming three species s1, s2, s3, the distance between s1 and s2 is given in the equation (3). With the third species s3, the temperature equation is given as:
AT = t(s) - (Us)(11)
D(s, s) = max(AT, AT)
Similar to equations (11) and (12), the distance between species s 2 and s 3 is given in equation (13).
D(s, s) = max(AT, AT)
In distance based approach, less difference input sequences are used. As consequence of this, it is proved that
AT < AT + AT3
Using the distance measure between various sequences in the set of sequence S, the distance matrix is constructed as given in equation (15):
DM = D ( sx , sy ) V x , y g S & x < y (15)
where is DM is distance matrix.
-
B. Constructing Guide tree
After forming the distance matrix (equation 15), a tree is constructed as a guide to align the sequences which called as Guide tree. Applying Unweighted Pair Group Method with Arithmetic Mean (UPGMA) approach, the guide tree is constructed [27]. Due to its less complexity than Neighbor-Joining (NJ) method, in this paper
UPGMA method is employed for constructing the guide tree. The UPGMA algorithm was introduced by Sokal and Michener in 1958. Based on the sequences clustering, this algorithm builds the trees in simple and fast manner.
The steps of this method are as follows:
-
1. A distance matrix is constructed by finding the distance between each sequences using the equation (15).
-
2. The sequences with the closest distance are identified and connected ie.
-
3. The distance matrix is reconstructed counting sequence1 and 2 as a group: ie.initially GT = empty tree
-
4. Identify the next closest sequences and the matrix is again rebuilt ie.
-
5. Further the closest sequences are identified and the matrix is rebuilt till all the sequences are connected to a rooted tree ie.
mx = min( DM ( D ( s ^, sy )) V x , y g S (16)
where is the minimum distance value between x and y in the distance matrix.
GT = GT u ( mx ( x , y )) V x , y g S (17)
GT = GT и ( m 2 ( x , y )) V x , y g S (18)
where is the next minimum distance value in the reconstructed matrix.
GT = GT u ( m 1 ( x , y ).... mt ( x , y )) (19)
where is the last minimum distance value in the finally rebuilt distance matrix. The Figure 5 shows a sample tree constructed from the distance matrix. In this zeros represents the distance between the two same sequences and ‘-‘ sign represents there is no value as we are going to consider the triangular values of the matrix. This is because in distance matrix upper triangular values are same as lower triangular values.
-
C. Aligning multiple sequences
5. No.
1
2
3
4
5
1
0
D(l,2)
D(l,3)
D(l,4)
D(l,5)
2
-
0
0(2,3)
0(2,4)
0(2,5)
3
-
-
0
0(3,4)
0(3,5)
4
-
-
-
0
0(4,5)
5
-
-
-
-
0
Using the constructed guide tree, the sequences are aligned. To align the sequences, progressive alignment approach [23] is employed in this paper. In this process as a first step, the sequences that have a common connection in the tree are taken for the alignment. The two sequences are aligned to find the consequence. In the second step, next commonly connected sequences are obtained to find the consequence. Using the consequence of the sequences, the subsequent nearest sequence of that set is considered for the alignment until all the sequences are aligned. Here, one of the serious pitfalls of the progressive alignment caused by the greedy approach is avoided. This is because, the distance between the sequences in the distance matrix are more accurate than other measures. So, the alignment using the guide tree is in the correct order.

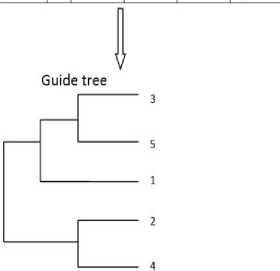
Fig.6. Guide Tree from Distance Matrix using UPGMA
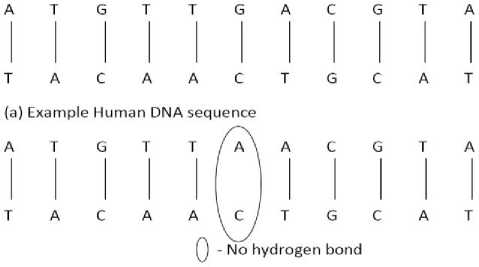
(b) Example Chimpanzees DNA sequence
Fig.7. Example DNA Sequence of Human and Chimpanzee
-
V. Discussion
In this paper, a theoretical study on a distance measure using melting temperature in DNA hybridization is discussed. Some of the sequence bonding is studied in detail and the melting temperature is assumed. Chimpanzee and Human DNA sequences are estimated that 95% of the base pairs are exactly shared between them [28].
The sample sequences for human and chimpanzee are represented in Figure 7. From the Figure 7, it is observed that the first three rows (human) are the sequence bonded strongly with the complementary base pairs and in the next set of three rows (chimpanzee) one unbounded base pair is seen. This shows that there is a small distance between these two sequences.
Table 1. Sample Data
|
S. No. |
Sequence Name |
|
1 |
European Human |
|
2 |
Mountain Gorilla Rwanda |
|
3 |
Chimp Troglodytes |
|
4 |
Easter lowland Gorilla |
|
5 |
Chimp verus |
Table 2. Denature Temperature
|
S. No. |
Denature T C |
|
1 |
98 |
|
2 |
95 |
|
3 |
92 |
|
4 |
94 |
|
5 |
93 |
Table 3. Denature Temperature T (deg. C) after Annealing with Different Species
|
S.No. |
2 |
3 |
4 |
5 |
|
1 |
94 |
95 |
94 |
93 |
|
2 |
92 |
94 |
93 |
|
|
3 |
93 |
92 |
||
|
4 |
93 |
Table 4. Distance Matrix using Melting Temperature
|
S.No. |
2 |
3 |
4 |
5 |
|
1 |
4 |
3 |
4 |
5 |
|
2 |
3 |
1 |
2 |
|
|
3 |
1 |
2 |
||
|
4 |
1 |
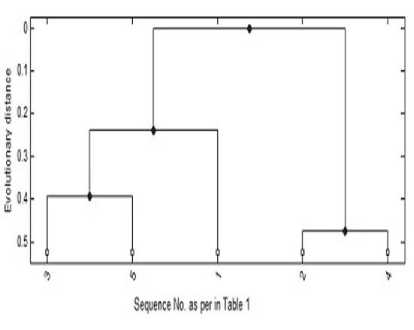
Fig.8. GT for Sample Data
In Table 1 sample data is specified. Starting with this assumption, the melting temperatures are calculated. In biology lab, DNA operations can be done by allowing a number of sequences inside a single test tube and heating it to a particular temperature. Each sequence denatures at different temperature should be noted. According to the study of the sample data sequences, denature temperature is assumed and given in Table 2. The values in Table 3 show the denature temperature after annealing with different species. Along with this temperature table and the equation (3), the distance matrix is constructed and given in Table 4. The guide tree constructed using this distance matrix that is shown in Figure 8 and the alignment in Figure 9.
The theoretical complexity of this process is O(1). In the worst case, if it is not correctly bonded with all the sequences, the complexity is assumed to be less than O(n). This approach is more efficient only for the dataset with long and large sequences.
European Human nCHTtoTGGGGMiGCAGaHTGGGTACCikCCCAAGTMTGACTTACCCMCAACAACCGCTATGTKnTCGTA:
Mountain Gorilla Rwanda TTCTTTCATGGGGAGACGAATTTGGGTGCCACCCAAGTATTAGTTAACCCACCAATAATTGTCATGTATGTCGTG:
Chinp_Troglodyces .........................GTACCACCTAAGTATTGGCCTAnCAT-TACAACCGCTATGTATnCGTA
Eastern Lowland Gorilla ncnTCATGGGGAGACGMATTTGGGTGCCACCTAAGTATTAGTTAACCCACCAATAATTGTCATGTATTTCGTG:
Chimp Verus .......................—GTACCACCTAAGTACTGGCTCATTCAT-TACAACCGGTATGTACTTCGTA
CATTACTGCCAGCCACCATGAATATTGCACGGTACCATAAATACTTGACCACCTGTAGIACATAAAAACCCAATCCACi CATTACTGCCAG2CACCATGAATAATGTACAGTACCACAAACACTCCCCCACCTATAATACATTAC2CCCCCTC---- CATTACTGCCAGCCACCATGAATATTGTACAGTACTATAACCACTCAACTACCTATAAIACATTAASCCCACCCCCACi CATTACTGCCAGCCACCATGAATAATGTACGGTACCATAAACACTCCCTCACCTATAATACATTACCCCCCOTC----- CATTACT GCCAGTCACCATGAATATT GT ACAGTACCATAATCACCCAACTACCTATAAIACATAAAATCCACTCCCACj
:atcaaaaccccctccccatgcttacaagcaagtacagcaatcaaccctcaactatcacacatcaactgcaactccaaa ------ACCCCCCATTCCCTGCTCAC----------------------------------------------------- :attacaacctccaccctatgcttacaagcacgcacaacaatcaacccccaactgtcacacataaaatgcaactccaaa ------ACCCCCCATCCCTTGCCCAC----------------------------------------------------- :accaaaaccttcaccccatgcttacaagcacgcacaacaatcaacctccaactgtcaaacataaaacacaactccaac
GCCACCCCTCACCCACTAGGATACCAACAAACCTACCCACCCTTAACAGTACATAGTACATAAAGCCATTTACCG" -----------CCCAA^GGCATACCAACCAACCTATCCCCTCACAAAAGTACATAATACATAAAATCATTTACCG' GACACCCCTCTCCCACCCCGATACCAACAAACCTATGCC2TTTTAACAGTACATAGTACATACAGCCGTACATCG------------CCCAACAGCATACCAACTAACCTACCCCTCTACAAAAGTACATAGTACATAAAATCATTTACCG-GACACCCCTCCCCCACCCCGATACCAACAGACCTA-CCCCCCTTGACAGAACATAGTACATACAATCATACACCG-
IACATAGCACATTACAGTCAAATCCCTTCTCGTCCCCATGGATGACCCCCCTCA---------------------- TCCATAGTACATTCCAGTTAAA-CCATCCTCGCCCCCACGGATGCCCCCCTTCAGATAGGGATCCCTTAAACACCA CACATAGCACAT - А^АСТСнллТ ^CAT CCT* GCCCC^A ■«- GGATGC ^-^CCCCTCA ^л i AGG™——————————————— TCCATAGCACATTCCAGTTAAA-CCATCCTCGCCCCCACGGATGCCCCCCCTCAGATAGGGGTCCCTTAAACACCA TACATAGCACATTACAGTCAAACTCTTCCTCGTCCCCACGGATGCCCCCCCTCAGATAGG----------------
Fig.9. Sample Data Alignment
-
VI. Conclusion
Aligning multiple molecular sequences, an NP-complete problem has been noted as a key research domain for more than a decade. As there is a trade-off between accuracy and computational time, there is a demand for different techniques for this MSA problem. Considering these points, an efficient technique is proposed in this paper. And, from the study of the traditional approaches, it is concluded that the distance measure based approaches yield better solution than others. This measure finds the distance among all the sequences to form a distance matrix. And according to this matrix the sequences are aligned. Here a novel distance measure is formed and proved using the distance function properties.
This paper discusses a theoretical study on a distance measure using the melting temperature in DNA hybridization for MSA problem, which is more suitable for a long and large dataset. The melting temperature during denaturing is used for the distance measure calculation.
Owing to its massive parallelism process the DNA operations are considered for this measure calculation. This approach uses less computational time and yields an approximate solution for the MSA problem.
As future work, the distance matrix can be formulated using the proposed distance measure using the laboratory temperature results.
Acknowledgment
This research has been supported and funded by the Ministry of Human Resource development (MHRD) under the government of India.
Список литературы A Novel Distance Metric for Aligning Multiple Sequences Using DNA Hybridization Process
- J. Thomopson, D.G. Higgins, T.J. Gibson, "ClustalW." Nucleic Acids Res 22, 4673 (1994).
- C. Notredame, D.G. Higgins, J. Heringa, "T-Coffee: A novel method for fast and accurate multiple sequence alignment." Journal of molecular biology 302(1), 205 (2000)
- C.B. Do, M.S. Mahabhashyam, M. Brudno, S. Batzoglou, “ProbCons: Probabilistic consistency-based multiple sequence alignment." Genome research 15(2), 330 (2005).
- K. Katoh, K. Misawa, K.i. Kuma, T. Miyata, "MUSCLE: multiple sequence alignment with high accuracy and high throughput." Nucleic acids research 30(14), 3059 (2002).
- B. Morgenstern, Bioinformatics “DIALIGN 2: improvement of the segment-to-segment approach to multiple sequence alignment." 15(3), 211 (1999).
- E. Depiereux, E. Feytmans, "MATCH-BOX: a fundamentally new algorithm for the simultaneous alignment of several protein sequences." Computer applications in the biosciences: CABIOS 8(5), 501 (1992).
- S.R. Eddy, "Profile hidden Markov models." Bioinformatics 14(9), 755 (1998).
- P.J. Van Laarhoven, E.H. Aarts, Simulated annealing (Springer, 1987).
- C. Notredame, D.G. Higgins, "SAGA: sequence alignment by genetic algorithm." Nucleic acids research 24(8), 1515 (1996).
- S. Hosangadi, “Distance measures for sequences” arXiv preprint arXiv: 1208.5713 (2012).
- T. Jiang, G. Lin, B. Ma, K. Zhang, “A general edit distance between RNA structures.” Journal of computational biology 9(2), 371 (2002).
- R.C. Edgar, "MUSCLE: multiple sequence alignment with high accuracy and high throughput." Nucleic acids research 32(5), 1792 (2004).
- Eddy, Sean R., and Burkhard Rost. "A probabilistic model of local sequence alignment that simplifies statistical significance estimation." PLoS Comput Biol4.5 (2008): e1000069.
- Y. Zhang, W. Chen, "A new measure for similarity searching in DNA sequences." MATCH Commun. Math. Comput. Chem 65, 477 (2011).
- Xu Li, ZhenzhouJi,"Efficient Parallel Design for Edit distance algorithm in DNA Sequence Alignment", IJEM, vol.1, no.4, pp.32-38, (2011).
- F. Naznin, R. Sarker, D. Essam, “Vertical decomposition with genetic algorithm for multiple sequence alignment." BMC bioinformatics 12(1), 353 (2011).
- G. Garai, B. Chowdhury, Journal of Biophysical Chemistry 3, 201 (2012).
- K.D. Nguyen, Y. Pan, “A Knowledge-Based Multiple-Sequence Alignment Algorithm." IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB) 10(4), 884 (2013).
- J. Sun, V. Palade, X. Wu, W. Fang, "Multiple sequence alignment with hidden Markov models learned by random drift particle swarm optimization." Computational Biology and Bioinformatics, IEEE/ACM Transactions on, Vol.11, no.1, pp: 243_257, (2014).
- M. Kaya, A. Sarhan, R. Alhajj, “Multiple sequence alignment with affine gap by using multi-objective genetic algorithm." Computer methods and programs in biomedicine 114(1), 38 (2014).
- Modzelewski, Michal, and Norbert Dojer. "MSARC: Multiple sequence alignment by residue clustering." Algorithms for Molecular Biology 9.1 (2014).
- Arabi E. keshk,"Enhanced Dynamic Algorithm of Genome Sequence Alignments", IJITCS, vol.6, no.6, pp.40-46, 2014. DOI: 10.5815/ijitcs.2014.06.06.
- Bodenhofer, Ulrich, et al. "msa: an R package for multiple sequence alignment." Bioinformatics (2015): btv494.
- Jayapriya, J., and Michael Arock. "A parallel GWO technique for aligning multiple molecular sequences." Advances in Computing, Communications and Informatics (ICACCI), 2015 International Conference on. IEEE, 2015.
- M. Amos, Theoretical and experimental DNA computation, vol. 4 (Springer, 2005).
- J.T. Wang, M.J. Zaki, H.T. Toivonen, D. Shasha, Introduction to data mining in bioinformatics (Springer, 2005).
- J. Xiong, Essential bioinformatics (Cambridge University Press, 2006).
- R.J. Britten, "Divergence between samples of chimpanzee and human DNA sequences is 5%, counting indels." Proceedings of the National Academy of Sciences 99(21), 13633 (2002).


