A novel evolutionary automatic data clustering algorithm using teaching-learning-based optimization

Published Online May 2018 in MECS

Evolutionary Algorithms (EA) are generic metaheuristic optimization algorithms that use techniques inspired by nature‘s evolutionary processes [1]. Instead of one single solution, EA maintain a whole set of solutions that are optimized at the same time. EA are able to provide a solution by approximation within adequately short time and have the ability to avoid getting stuck in local optima [2]. These algorithms searches input parameter values called solutions and results most favorable output parameter values [28].

TLBO proposed by R.V.Rao et.al. [3-9], in 2011, 2012 and 2013 is classified into this category. This nature-inspired meta-heuristic optimization algorithm is used in this work as an underlying psychometric model to automatically find optimal number of clusters for data clustering problem with less computational effort and high reliability.

Clustering, one a primitive theme in machine learning and data mining is an active research area and its applications are tremendously found in various in numerous fields such as pattern recognition, bioinformatics, data analysis, data mining and scientific data exploration [27]. Clustering also known as unsupervised classification is used to determine the intrinsic grouping in a set of unlabeled data, where the objects in each group are indistinguishable under some criterion of similarity [15]. Conventional clustering, needs input parameters to group and render best partitions in a given dataset, and supplemented with reliable guidelines to evaluate the clusters. The procedure of evaluating the results of a clustering algorithm is known under the term cluster validity [26]. CVIs are classified in to three categories: internal, external and relative, these CVIs are defined by combination of separability and compactness. Separability indicates how distinct the two clusters are, and compactness is used to recognize the closeness of cluster elements [27].

This work uses the following four external indexes Rand Index (RI) [10], Advanced Rand Index (ARI) [10], Hubert Index (HI) [11], Silhouettes (SI) [12], and two internal indexes Davies and Bouldin (DB) [13], Chou (CS) [14], measures to evaluate the clustering quality by the similarity of the pairs of data objects in different partitions.

The simple k-means conservative methods [24-25], has drawbacks in its key characteristics, i.e. the users need to have domain knowledge on the dataset to fix the number of clusters in advance, which is not always feasible in most of the cases, to the armature users, and data points assigned to a cluster cannot move to another cluster. Therefore, clustering became a mind-numbing trial-and-error work and its result are often not much promising especially when the number of natural partitions are large and not easy to guess. In few cases, these pitfalls may even fail to separate overlapping clusters due to lack of a priori information about the global shape or size of the clusters to armature users and hence they become computationally expensive. So, these challenges, compelled us to present a work in this direction to do automatic clustering, with a novel meta-heuristic find an optimal number of automatic clusters.

The anticipatory work in this paper proposes a novel evolutionary algorithm (AutoTLBO) with elitism to gain an effectual conservation towards performing automatic clustering. The proposed algorithm is appropriate in determining the optimal number of clusters in the data set automatically without any human intervention. This algorithm uses simple k-means to derive automatic clusters without any a priori initialization of number of clusters, and once the clusters are derived, they are endorsed with CVIs to estimate compact cluster structures in the given data set.

The rest of the paper is organized as follows: Section II presents related works taken up in this direction. Section III contains fine-tuned arrangement of TLBO. Section IV contains anticipated automatic clustering using TLBO. Section V presents the study comparative of results obtained and discussion on findings from benchmark and synthetic datasets. Finally, conclusion is drawn by epigrammatic involvement and further work.

• II.    Related Works

Automatic clustering had a passive on looking in the recent past and the number of publications are thwarted, by rendering clusters with panoramic cluster structures. The objective of any automatic algorithm is to discover the natural groupings in the given data. Choosing k is a nagging problem in cluster analysis, and there is no agreed upon solution. For this reason, clustering is a form of learning by observation, rather than learning by examples [20]. Reference [21] proposed automatic clustering loom with fitness functions for finding optimal number of centroids and clusters using evolutionary programming. Automatic Clustering using Differential Evolution (ACDE) algorithm proposed by [17] portray the applicability of Differential Evolution (DE) to partitioned clustering techniques, thereby automatically cluster, and produce optimal number of clusters from the unclassified objects in datasets. Differential Evolution has materialized as one of the quick, robust, and proficient global search heuristics in progress. It is easy to apply and requires a trifling quantity of parameter tuning to attain noticeably good search results [22]. The authors of reference [23] focused on a use of specific crossover and mutation operators in the computational steps of DE.

Similarly, to any existing population based algorithms, TLBO has a set of populations as inputs, learners are characterized using solution vectors and dimensions of each vector are expressed as subjects. The pragmatic outcome from TLBO is the unsurpassed learner is always the teacher. TLBO was first introduced and demonstrated by [3-4] to obtain better optimization performance in many fields of engineering, the constrained mechanical design optimization problems, unconstrained and constrained real-parameter optimization problems, continuous non-linear large-scale problems, and comparison with other evolutionary optimization algorithms, a number of improvements and applications concerning TLBO has been proposed sequentially [3-9] compared TLBO against classical K-means clustering and PSO clustering.

• III.    Teaching-Learning-Based Optimization

This algorithm mimics the teaching-learning ability of teacher and learners in a classroom. The principle idea involved in TLBO is the simulation of teaching process in the traditional classroom. The performance of TLBO ends in two basic stages: (1) “teacher phase” or learning from the teacher, and (2) “learner phase” or trade off information between learners. Teacher is the one who promotes students knowledge to the best of his or her current level.

The implementation of TLBO requires only the assertion of controlling parameters like population size, number of generations, and this causes the algorithm to be an algorithm-specific parameter-less algorithm. This embedded feature in TLBO attracted us to use this algorithm towards evolutionary automatic clustering automatic problems.

The outputs of TLBO algorithm are considered in terms of results of learners, implicitly estimating the quality of teacher. Since, teacher is usually considered as a highly learned person who trains learners. Moreover, learners also learn from the interaction among themselves that also helps in improving their results.

• A.    TLBO Methodology

Teacher phase: In this phase learners are trained under the teacher and the teacher tries to increase the mean result of the classroom from any value A 1 to his or her level F_A. Considered A j be the mean and F i be the teacher at any iteration i, F i will try to improve the existing mean A j towards the new mean, designated as A_new, and give the difference between the existing mean and new mean is shown as

Residue_Meani = ri(Anew - TfAj). (1)

where 7 is the teaching factor, which decides the value of mean to be changed, and ri is the random number in the range [0, 1]. Using 7 with a value 1 or 2 is a heuristic step used to decide equal probabilities randomly as:

Т у = round[1 + rand(0,1){2 - 1}].     (2)

The value in teaching factor, 1 indicates no change of knowledge and 2 indicates to complete transfer of knowledge to learner. The intermediate values indicate amount of transfer level of knowledge, depending on learner’s capabilities. Based on this Residue_Mean, the existing solution is updated as

L new,i = L oid,i + Residue_Mean i .      (3)

Learner phase: In this phase learners enhancing their knowledge level by interaction among themselves randomly. This phenomenon is expressed in form of iteration i, by considering two different learners L i and L j where i ^ j.

^Lnew,i = ^Lold,i ^{+ r}i⁽ L i - L j ) if ^f(Li ) < /(L j ).     ⁽⁴⁾

L new,i = L oid,i + r i (L j - L i ) if f(L j ) < /(L i ).   (5)

• B.    Elitist TLBO

Elitist TLBO algorithm proposed by R.V. Rao et al. [67] solved both constraint and unconstraint multi-objective optimization problems. This mechanism upholds the best individuals from iteration to iteration both in teacher and learner phases, so that the algorithm never loses the best individual in the optimization process [6-7]. In TLBO algorithm, after replacing the worst solutions with elite solutions it is necessary to modify the duplicate solutions in learner phase so that they are avoided from getting trapping in local optima. Duplicate solutions are modified on randomly selected dimensions of the duplicate solutions before executing the next iteration. So the total number of function evaluations in the elitist TLBO algorithm is equal to {(2 × population size × number of generations) + (function evaluations required for duplicate elimination)}.

• IV.    Evolutionary Automatic Data Clustering Algorithm using Tlbo

The proposed Automatic Clustering (AutoTLBO) implants k-means partitioned clustering algorithm and CVIs into TLBO algorithm with elitism. The proposed algorithm works in two folds. The first fold assumed as cluster configuration phase applies the core logic of k-means clustering using the teaching and learning phases of TLBO and finds optimal number of clusters automatically. The second fold assumed as cluster assessment phase simultaneously optimizes multiple CVIs as fitness function to appraise the generated clusters.

• A. AutoTLBO Algorithm

Cluster Configuration phase

Step 1: Initialize each learner randomly with Maxk number of selected cluster centers within the activation thresholds in [0, m] and population P randomly initialized to a dataset with n rows and d columns.

P i,j (0) = P™ⁱⁿ + rand(1) * (P j ^max - P™ⁱⁿ).     (6)

where P ij is a population of learners and i^th learner at current generation g with s subjects is shown as

Step 2: Find active cluster centers > 0.5, in each learner and keep them an elite solution using (1)

Step 3: For 5 = 1 to g _max do

• a.    Compute Euclidean distance for each data vector P _g from all active cluster centers.

• b.    Consign P _g to nearby cluster

• c.    Recalculate the location of k-centroids, when one the objects are allotted

• d.    Repeat Step 2 and 3 until the centroids no longer move

• e.    Adjust duplicate solution before rolling to next iteration via randomly selected dimensions using (2) and (3)

Cluster Assessment phase

Step 4: Appraise each learner quality and find Teacher, as best Learner using Rand Index

Step 5: Revise learners using (4) and (5)

Step 6: Repeat step 2 through step 5 until stoppage condition is met. Display the attained final solution as global best learner at time g = g _max .

• V.    Experimental Analysis and Discussion

  The experiments are performed on Intel core i3CPU 530@2.93GHz desktop computer with 4 GB RAM memory on 32 bit windows operating system. The software is developed using mat lab R2011a. The benchmark datasets iris, wine and glass are extracted and preprocessed from UCI repository [16].

• A.    Experiment 1

In this experimental analysis, algorithms that support automatic initialization of initial seeds are used, and to evaluate its effectiveness the acquired results of proposed work over synthetic and benchmark data sets are compared along with CVIs after posteriori phase. The mean function evaluation of CVI, percentage of error rate and CPU time is wormed as criteria for these methods. The mean values of CVIs, i.e. ARI, RI, SIL, HIM, CS, DB after applying 50 independent runs over auto clustering algorithms ACDE [17], AutoGA [18] and AutoTLBO [19] is presented in Table 1. The number of automatic clusters engendered after posterior phase of each algorithm is moreover revealed in Table 1. The annotations from Table 1 speculate a thumbnail sketch of AutoTLBO supremacy in automatic clustering algorithms. The best entries and front-runners in Table 1, 2 and 3 are marked in boldface.

In case of Iris dataset, AutoTLBO has outperformed all the algorithms except for ACDE when pertained over the DB index, but convergence of error rate shown by ACDE is better than AutoTLBO. An important examination was AutoTLBO shows a paramount value in k while originating the optimal auto clustering and is even fortunate to put an optimal usage of 27.89 m.sec CPU time. Mixed fallout of AutoTLBO is observed in Wine dataset at both the error rate and number of optimal auto clusters shaped, accelerated performance is attained with CVIs like ARI, HIM, SIL and CS. A major deliberation was that the k value is not closer to actual number of clusters and ACDE attracts the advantage with k value as 3.26. This experiment shows that AutoTLBO is effective in terms of effort of CPU computational time effort, consistency and obtaining the splendid solutions in CVIs. The Preeminence of AutoTLBO is again noticed on the Wine dataset, since appropriate values are gained on the ARI, RI, CS and SIL CVIs. The minimal dispensation of CPU time, massive dips in percentage of error rate to 47.20 are affirmative indications to justify AutoTLBO is noteworthy.

Table 1. Mean values of automatic algorithms after completion of 50 independent runs

Datasets	Algorithm	No. of Auto Clusters	ARI	RI	SIL	HIM	CS	DB	% of Error Rate	CPU Time (M Sec)
Iris	AutoTLBO	3.02	0.9232	0.9737	0.0763	0.9473	0.7194	0.5178	6.00	27.89
	ACDE	3.06	0.9124	0.9613	0.0387	0.9226	0.7905	0.4373	2.67	397.86
	AutoGA	3.15	0.8144	0.9147	0.0219	0.8746	0.8358	0.6014	13.46	489.55
Wine	AutoTLBO	3.5	0.6932	0.6842	0.3158	0.5683	0.3955	0.7693	51.22	37.16
	ACDE	3.26	0.4107	0.7243	0.2757	0.4485	0.3842	0.8326	32.02	537.62
	AutoGA	4.2	0.5489	0.6779	0.1169	0.5631	0.3668	0.7136	70.22	1149.41
Glass	AutoTLBO	5.86	0.6553	0.7053	0.2947	0.4107	0.2991	1.3009	47.20	41.67
	ACDE	5.8	0.3266	0.7329	0.2671	0.4657	0.2745	1.2443	57.10	708.15
	AutoGA	5.4	0.4785	0.7234	0.2444	0.3999	0.2638	1.2847	68.78	963.25
Synthetic Dataset-1	AutoTLBO	2.5	0.5861	0.7926	0.0002	0.5853	0.4331	0.3748	16.20	82.50
	ACDE	2	0.9982	0.9991	0.0009	0.9982	0.8305	0.4647	0.00	827.57
	AutoGA	3.5	0.5669	0.7412	0.2010	0.8852	0.4178	0.5467	36.41	658.27
Synthetic Dataset-2	AutoTLBO	4.02	0.9896	0.9590	0.0110	0.9679	0.7777	0.4083	11.00	106.63
	ACDE	4.04	0.9481	0.9801	0.0199	0.9602	0.7778	0.5100	2.20	1620.50
	AutoGA	4.51	0.8896	0.9231	0.0445	0.9247	0.7041	0.5987	19.21	1836.56
Synthetic Dataset-3	AutoTLBO	3.16	0.7983	0.9968	0.0132	0.9937	0.8166	0.3290	6.00	55.57
	ACDE	3.02	0.9740	0.9885	0.0115	0.9769	0.8173	0.4822	1.00	841.36
	AutoGA	3.56	0.9425	0.9638	0.0147	0.9845	0.8236	0.6987	14.33	1295.33
Synthetic Dataset-4	AutoTLBO	6.7	0.9951	0.9986	0.0014	0.9973	0.9586	0.1434	0.00	170.95
	ACDE	6.84	1.0000	1.0000	0.0020	1.0000	0.9749	0.1620	0.00	2737.79
	AutoGA	6.90	0.9961	0.9426	0.0095	0.9923	0.9635	0.1688	0	3098.74
S-Shape	AutoTLBO	1.9	0.4343	0.6973	0.3070	0.2346	0.2379	2.2022	0.40	134.72
	ACDE	2	0.3765	0.6882	0.3118	0.3765	0.3204	1.8403	17.38	186.49
	AutoGA	1.7	0.2827	0.5876	0.3333	0.3632	0.4783	1.945	19.33	235.33
Nested Circles	AutoTLBO	3.02	0.2084	0.6470	0.4530	0.2940	0.3390	0.9527	81.71	69.66
	ACDE	3.48	0.1978	0.5899	0.4601	0.1797	0.3776	1.0970	37.56	109.58
	AutoGA	3.33	0.2001	0.5558	0.4781	0.2222	0.3441	1.00	44.28	149.74
Two close half-moons	AutoTLBO	1.8	0.2908	0.6439	0.2561	0.7877	0.3941	0.8836	51.44	160.55
	ACDE	2	0.4295	0.7149	0.2851	0.4298	0.6150	0.8959	18.33	220.88
	AutoGA	2.4	0.4112	0.7044	0.2744	0.5896	0.6247	0.9043	44.32	281.32
Two joint circles	AutoTLBO	2	0.4151	0.6926	0.3174	0.4051	0.1022	2.0639	47.60	63.05
	ACDE	2	0.3420	0.6728	0.3272	0.3457	0.2564	2.1621	30.80	85.14
	AutoGA	2.5	0.2259	0.5891	0.3301	0.4000	0.2478	0.2147	49.55	109.22
Two separate circles	AutoTLBO	1.76	0.7660	0.9701	0.3299	0.8402	0.2235	1.1660	23.33	84.73
	ACDE	2	0.7938	0.8984	0.1016	0.7969	0.4773	1.2457	3.00	118.77
	AutoGA	2.09	0.7111	0.9558	0.3348	0.8556	0.3478	1.1198	30.45	658.34
Two separate half-moons	AutoTLBO	2.0	0.6480	0.8741	0.3259	0.7482	0.1533	1.2067	10.50	129.79
	ACDE	1.98	0.5605	0.7802	0.2198	0.5605	0.3790	1.6246	11.00	186.28
	AutoGA	2.31	0.4874	0.5584	0.2214	0.5584	0.3694	2.2584	22.95	269.14

Table 2. Minimum and Maximum error rate of automatic clustering algorithms after 50 independent runs in special shaped datasets

Error Rate	Algorithms	Special shaped datasets
		S-Shape	Nested Circles	Two close half-moons	Two joint circles	Two separate circles	Two separate half-moons
Min	AutoTLBO	14.6300	0.2065	0.3096	0.3099	0.5199	0.6127
	ACDE	0.4250	0.3171	0.3669	0.3142	0.8817	0.6079
	AutoGA	20.2478	0.8471	0.8521	0.4112	0.6847	0.7841
Max	AutoTLBO	41.2108	0.8740	10.4710	11.3240	15.4752	21.000
	ACDE	14.3581	15.3201	12.3654	14.3654	21.3694	22.3140
	AutoGA	58.3654	21.3690	10.5419	10.2354	20.3200	22.3641

Table 3. Minimum and Maximum error rate of automatic clustering algorithms after 50 independent runs in synthetic and real-time datasets

Error Rate	Algorithms	Synthetic datasets				Real-time datasets
		1	2	3	4	Iris	Wine	Glass
Min	AutoTLBO	0.8330	0.8977	0.8330	1.000	0.8347	0.3629	0.3132
	ACDE	1.0000	0.9442	0.9703	1. 0 00	0.9222	0.4382	0.3270
	AutoGA	0.0000	1.0000	2.0000	0.000	3.3333	28.0898	39.7196
Max	AutoTLBO	47.218	58.774	80.100	37.74	53.911	67.1524	85.5743
	ACDE	0.2850	66.333	80.800	37.75	62.666	78.6516	88.7850
	AutoGA	52.570	62.333	82.200	37.75	56. 6 66	69.1011	86.9158

In the case of synthetic data set1, AutoTLBO produces the optimal clustering value for SIL, DB and near optimal mean value for RI and ARI and moderate mean value for HIM and CS CVIs. The error rate also drops relatively when AutoTLBO is compared with AutoGA but over headed by ACDE. The number of clusters generated by AutoTLBO automatically was 2.5 and may be rounded to 2. Hence sensible impact of AutoTLBO is observed on synthetic data set 1. The supremacy of AutoTLBO is exhibited evidently when penetrated through synthetic dataset 2. The CVIs ARI, SIL, HIM, DB produce optimal values towards its frontiers, the number of clusters automatically generated is 4.02. ACDE laterality is noticed only on percentage of error rate but it is expelled with the impact of AutoTLBO CPU time. Synthetic dataset 3 replicate the same tendency by exhibiting finest mean values of RI, HIM, CS, DB CVIs, optimal number of auto clusters may be rounded to 3. A fact to be assimilated was the error rate yet to be sorted and spur growth in CPU time always lauded. The goodness of clustering is hard-nosed especially in the case of synthetic dataset 4. Optimal number of clusters is consequent automatically to 7. The CVIs of SIL, CS and DB are optimal; RI, ARI, HIM are in close to proximity. The convergence in error rate and CPU time of AutoTLBO is comparatively low with other auto clustering methods.

The jumble of experiences farmed at optimal number of automatic clusters, error rate, CPU time and optimal convergence in ARI, RI, SIL, CS, CVIs persuade the golden chalice of AutoTLBO over S-shape dataset. Strong and resurgent automatic clusters, CPU time, discrimination in ARI, RI, SIL, HIM CVIs is perceived by AutoTLBO in nested circles dataset but with sycophancy in percentage of error rate. In the two close half-moons dataset AutoTLBO doldrums in conceding of automatic clusters and percentage of error, but forceful and consistent interventions of CVIs SIL, HI, CS, DB and CPU time allay AutoTLBO immensely as a challenger auto clustering method to AutoDE. The two joint circles dataset bring backs AutoTLBO as an organizational conundrum in the aspects of accurate number of automatic clusters, optimal mean values in all the CVIs and CPU time.

Ungrudging comfort was given by AutoTLBO in the two separate circles dataset in respect to the optimal number of automatic clusters, percentage of error rate and moderate performance in ARI and SIL. Perceptible CPU time and quickened performance in accomplishment of optimal clusters with CVIs like RI, HIM, DB and CS empowers AutoTLBO as a mediocrity mess towards automatic clustering algorithms. There were corroborating and colluding opportunities to AutoTLBO over the two separate half-moons dataset where it provoked exact number of automatic clusters, optimal mean value of CVIs, depression in error rate and CPU time. The plethora of automatic clustering algorithm ACDE, AutoGA and AutoTLBO over synthetic and real time data sets were manifested according to their significant value at CVIs. The depiction was AutoTLBO pats as a best performer in most of the cases and in few, it holds the equivalent performance as a front-runner with its competitors.

• B.    Experiment 2

In this experiment 2, the minimum and maximum error rates of each auto clustering algorithm after applying 50 independent runs on special shaped, synthetic and realtime datasets are considered and the same is revealed in Table 2 and Table 3. Interestingly, the minimum error rate of synthetic datasets 1, 2 and 4 is same with its contestant algorithms steeping towards the minimal rate. Similarly convincing low minimal error rate is observed in AutoTLBO when pertain with all the benchmark datasets. As far as maximum error rate is considered, AutoTLBO had made its smudge both in synthetic and real-time datasets exhibiting low minimal value in maximum error rate, except with a variation in synthetic dataset 1. The impression after conducting experiment 1

and 2 is that AutoTLBO dominates its competitor auto clustering algorithms in a statistically significant manner. Most of the entries in Table 1 and Table 2 and Table 3 confirm the fact that AutoTLBO algorithm remains clearly and consistently superior to the other competitors in terms of the accuracy in auto clustering. Substantial performance difference is documented during the runs and it verdicts that AutoTLBO abide with the promised endeavors. This experiment shows that AutoTLBO is effective in terms of computational effort, consistency and obtaining the optimum solutions.

• C.    Experiment 3

The panoramic rendering of cluster engendered in iris benchmark dataset and synthetic dataset 1-4, and special shaped datasets using AutoTLBO algorithm are visualized in as Fig. 1, Fig. 2, and Fig. 3. These holistic approaches commemorate AutoTLBO method with plethora of opportunities towards producing automatic clusters.

Fig. 1 upholds the clusters stimulated by automatic clustering methods with AutoTLBO, ACDE, and AutoGA in iris dataset. The clusters instigated by the adduced AutoTLBO were more precise to the real clusters when segregated with the divergent methods. Fig. 2 (a-d) envisages the clusters rendered by AutoTLBO over the Synthetic datasets 1-4.

The automatic clusters attained over these datasets are fair enough and transparent when compared to the tangible values. This opportunity leads to the resurrection of AutoTLBO and dominance over the automatic clustering algorithms. Fig. 3 (a-f) conceive of wide ranging auto clusters using AutoTLBO. All these prearranged fashioned clusters are time-tested and globally proven shapes practiced by early researcher’s regime and the present dispensation follow that precedent.

It is apparent from Fig. 3 (a-f) that the refitted version of TLBO is productive and substantive in producing the automatic clusters. Hence it is evident that all the experiments rationalize the proposed AutoTLBO is selfreliance and highly competitive in the arena of automatic clustering algorithms. Further, spur growth in CPU computational time, minimal error rate, in-bound CVIs values were the corroborating and colluding lay the way out to the AutoTLBO conundrum.

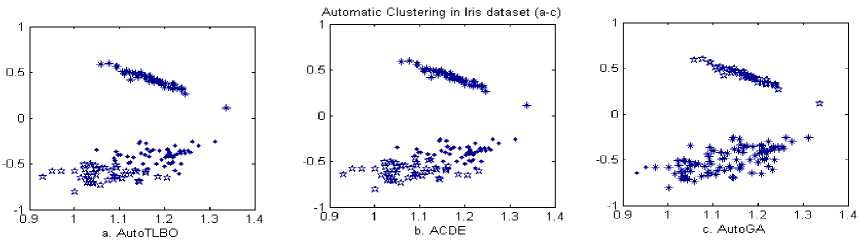
Fig.1. Panoramic rendering of automatic clustering algorithms in iris datasets

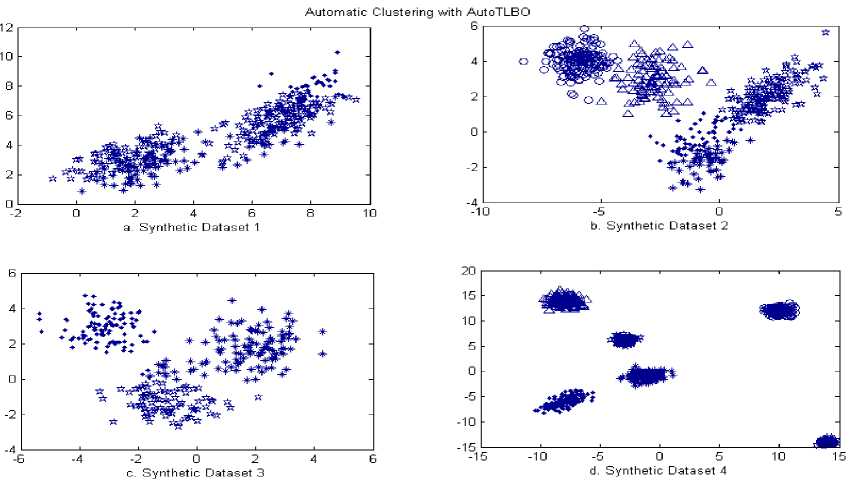
Fig.2. (a-d). Panoramic rendering of AutoTLBO in synthetic datasets 1-4

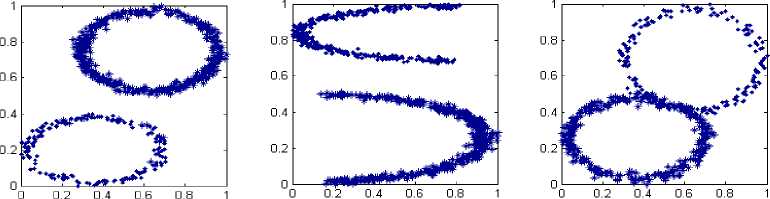
a. Two Seperate Circles                    b. Two Seperate Half Moons                      c. Two Joint Circles

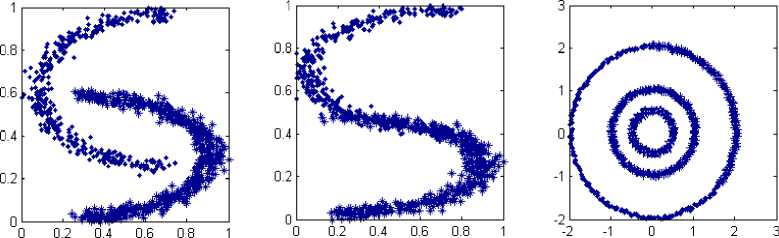
d Two Close Half Moons                            e S Shape                                f. Nested Circles

Fig.3. (a-f). Panoramic rendering in special shaped datasets using AutoTLBO

I.                            Frontiers of CVls                Frontiers of CVls                        .                                   .                                   .

Frontiers of CVls                   _                      _ _ _ _            Frontiers of CVls             Frontiers of CVls             Frontiers of CVls

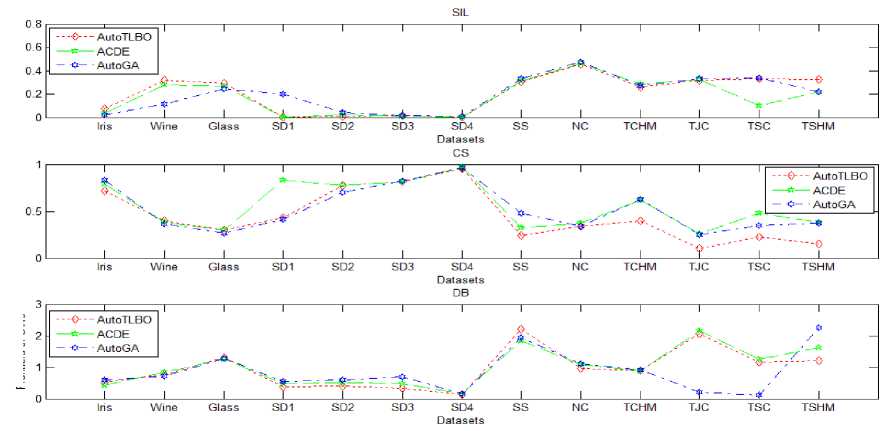
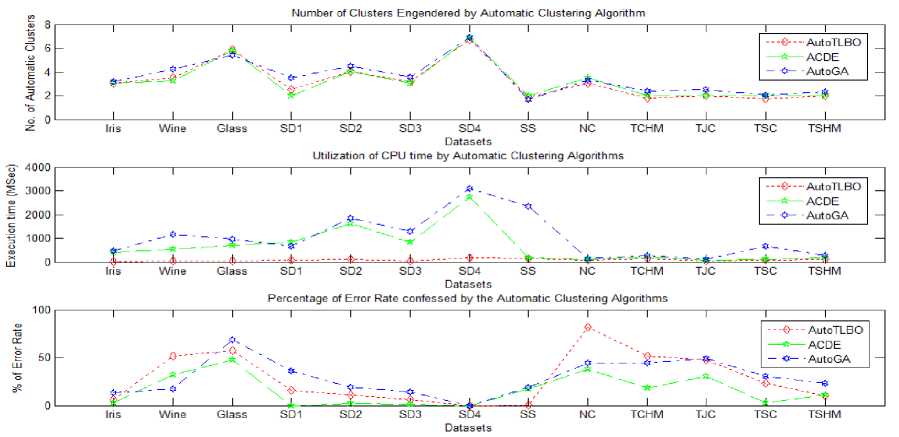
Fig.4. Reckoning values of automatic clustering algorithms in CVIs circumscriptions and other performance evaluation metrics

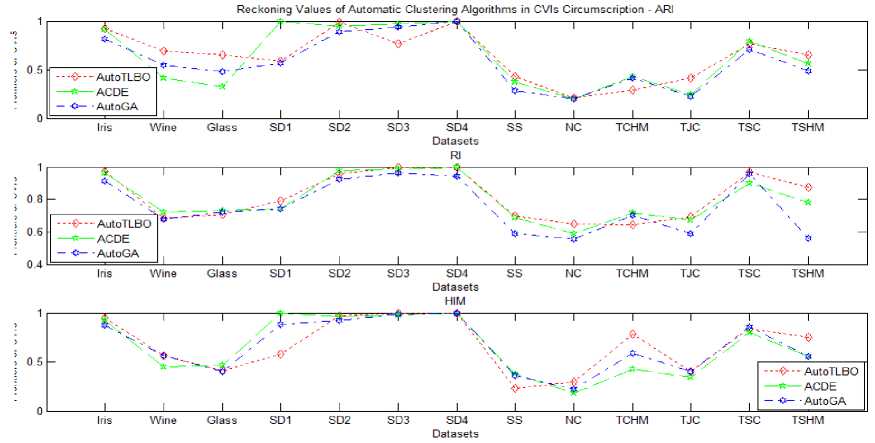
Fig. 4 persuades x-axis with all the 13 datasets mentioned in Table 1 and CVIs significance frontiers are sketched on y-axis. The plethora of automatic clustering algorithm AutoTLBO, ACDE and AutoGA over benchmark, synthetic and special shaped datasets is manifested according to their significant value at CVIs. An essential indulgence from Fig. 4 was AutoTLBO depose the contender algorithms in almost all the cases, by bolting optimal and close proximity CVIs values in its circumscription. The proposed AutoTLBO engender legitimate cluster fallout with accuracy and minimal error rate when collated with the serveralized algorithms. The proffered AutoTLBO provoke genuine clusters with veracity, low CPU time and nominal error rate.

The goodness of clustering is pragmatic by rendering optimal number of clusters automatically in most of the datasets. Similarly, the convergence in error rate and CPU time of AutoTLBO is comparatively low with other auto clustering methods. AutoTLBO had made its smudge in all datasets exhibiting low error rate, except with a variation in wine and nested circles datasets. Hence AutoTLBO has outperformed all the algorithms and these holistic approaches commemorate AutoTLBO method with plethora of opportunities towards producing automatic clusters.

• VI.    Conclusion

This paper elevated a novel AutoTLBO uses a population of solutions to proceed to the global solution. The effectiveness of AutoTLBO method is checked by means of different performance criteria like mean value of CVIs, convergence error rate, CPU time and number of automatic clusters. Ever since most of the clustering algorithms are arbitrary and very sensitive to their input parameters, it is very essential to evaluate the evaluating the righteousness of clusters dwelled. At the end the proposed AutoTLBO algorithm is able to outperform other automatic clustering algorithms in a meaningful way over a majority of artificial and benchmark data sets. The future research inclinations are to tailor the proposed algorithms with cluster applications in medical imaging, and image segmentation.

The insight gained from this paper is the proposed novel and integrated approach of merging simple k-means into TLBO is pragmatic. The two folds of proposed method are wide open and may encourage solicitations to one more fold embedded with preprocessing algorithms on of data set. Partitioned clustering algorithm in cluster configuration fold may be replaced with any hierarchical, density based, grid based, model based, hybrid, and evolutionary clustering algorithms. The cluster assessment fold may use any internal, external or relative CVIs according to the clustering application.