A Novel Image Encryption Scheme Based on Reversible Cellular Automata and Chaos

Published Online November 2019 in MECS DOI: 10.5815/ijitcs.2019.11.02

With development of communication, computer networks and digital multimedia, information security has become important. This development has some problems such as illegal copy and distribution of digital media. To solve this problem, some methods have been proposed [1,2].

Cryptography is one of the most common methods for information security. It derived from reversible mathematical operation and a set of rule-based calculations called algorithms for generating key of cryptography. Mathematical operations and keys are used to transform multimedia contents in ways that are hard to decryption. The encryption key is considered as the main element in cryptography, so that without the key, even with knowing the algorithm, decryption is impossible [3].

Digital images are greatly used in multimedia applications recently. These images contain private information in business, military, political, medical and the privacy of visual information is also important [2].

Text encryption algorithms are not suitable for images since these methods require a long computational time and power. Also, images are different from text due to dependency of its pixels. Therefore, special encryption methods are presented for image encryption [4].

Substitution and scrambling are main image encryption methods. Scrambling changes, the arrangement of pixels in the image. In this method, the position of the pixels changed and the encrypted image is obtained. At the destination, according to a recursive process, the initial arrangement of the pixels is obtained [5-7].

In substitution, the value of the pixels is changed by logical and computational operations and then in destination reverse encryption method is performed to retrieve pixel values [8-10].

Cellular Automata (CA) with its inherent characteristics such as the possibility of parallel processing, uniformity, unpredictability of behavior and simple implementation is suitable for image encryption. CA were introduced in 1940's by Von Newmann [11]. After introducing of CA, extensive studies have been done on it. In recent years, CA have been used in cryptography [12-14], image processing [15] and information security [16,17].

The disadvantage of CA includes that it is not inherently reversible, so that only a limited number of rules are reversible. So cryptography using these limited rules does not have the complement security [25,26]. Therefore, we propose a reversible CA in this study. In reversible CA, the new state of a cell is determined not only by the cell itself and its neighbors one step back but also by the cell itself two steps back.

In this paper, image cryptography is provided using both elementary CA and a reversible CA. In this method the combination of substitution and scrambling has been used. We use two reversible CA for substitution and an elementary CA for scrambling; so the proposed structure consists of three automata and image cryptography is performed in three steps. It should be noted that the proposed structure is reversible and by applying each step reversely, decryption is performed.

• II.    Related Work

  In 2008, Ruisong introduced a method for image encryption using CA. He first generated a sequence of random numbers using CA. Then, he scrambled the image using these [18].

In 2013, Fasel-Qadir et al. proposed digital image scrambling based on two dimensional cellular automata. He used CA for random number generator [19]. It should be noted that image scrambling techniques do not have high security due to the lack of histogram changes.

In 2012, Jin introduced a method for image cryptography using CA [20]. It was a simple image encryption method based on Elementary Cellular Automata (ECA). State attractors generated by ECAs under certain evolution rules perform the encryption function to transform pixel values of image, and the encrypted image is obtained. This method has a periodic behavior. Periodicity means a series of successive rules can be used in rotational way to achieve the original image.

In 2013, Abdo proposed a method based on pixel substitution. In this method, a linearly array of cells with a periodic behavior are generated by CA [21]. In this method loops of recursive rules are formed, and it used to encrypt and decrypt image periodically. In both of above methods, due to the periodicity of the algorithm, there is the possibility of attack and image decryption.

In 2013, Wang proposed a method based on pixel scrambling and substitution [22]. In the scrambling section, reversible CA were used. Substitution was performed only on low-value 4 bits. Therefore, the chance of randomness in this method is less and not suitable for encryption.

In 2014, Mohamed presented a blocking method for cryptography of the image using recursive CA [23]. In this method by using reversible CA, a pseudorandom permutation is first constructed, and then it injected into a parallelizable encryption schema that act on the different blocks of a digital image independently. This method performs well on multi-processor platforms and need powerful hardware implementation.

• III.    Cellular Automamta

CA is a mathematical model for discrete dynamic systems consisting of a number of cells. These cells form a network that can have different dimensions. CA has four components in the form of CA = {C, S, V, F}. The component C indicates the automata cell and S indicates the cell state. In most applications, the cells have two states of zero and one. The component V indicates the dimensions of the automata and the type of neighborhood. The component F indicates the rules for the transfer of CA [24].

A sample of CA including one-dimensional neighborhoods and a periodic boundary state with the transfer rule 30 is shown in Table 1. The first column shows eight possible states for cells with radius neighborhood 1 and second column shows the next state of each cell. The rule number 30 is placed binary in the second column.

Table 1. Elementary CA with Rule = 30

Q t —1 ft — 1 ft —1 S i , j — 1 S i , j S i , j + 1	S i t , j
000	0
001	1
010	1
011	1
100	1
101	0
110	0
111	0

In Table 2, the initial input vector of the automata is considered as [0 1 1 0 1 0 1 1]. To apply rule number 30 and 1-D neighborhood to determine the next state, the following procedure is applied. Given the 1-D neighborhood, the first three pixels [0 1 1] are selected. According to the rule 30, the next state is considered 1. Similarly, for the next three pixels, the rule [1 1 0] is applied and the next state of the cell becomes 0. This process continues for the other pixels. For the first and last pixels, the periodic boundary state is considered. The general trend up to 2 steps is shown in Table 2.

Table 2. Example of Elementary CA with Rule = 30

Input vector	01101011
1-d neighborhood	101	011	110	101	010	101	011	100
Next state	0	1	0	0	1	0	1	0
Output vector Of step 1	01101011 01001010
1-d neighborhood	001	010	100	001	010	101	010	100
Next state	1	1	1	1	1	0	1	1
Output vector Of step 2	01101011 01001010 11111011

• IV.    Reversible Cellular Automamta

CA are not inherently reversible, so that only a limited number of rules are reversible. In order to have a proper cryptography algorithm, the mathematical operation should be reversible. Cryptography using these limited rules does not have the complement security [25,26]. Therefore, we decided to use a reversible CA in this study.

In reversible CA, the new state of a cell is determined not only by the cell itself and its neighbors one step back but also by the cell itself two steps back (time(t-1) and (t-2)) [27,28].

For each cell of two step back (time (t-2)), there are two states of zero and one. In addition, for each cell and its neighbors one step back (time (t-1)) for 1-D neighborhoods, eight states can be defined. These two times are shown in Table 3. According to the rule number, we can determine the cell state for time t. In this method, two rules are considered for automata ( R 1 and R 2 = 2ⁿ-R 1 -1 ). This is shown in the second column of table 3 for two rules of 30 and 225.

Table 3. Reversible CA with R 1 = 30 and R 2= = 225

Q t —1   t— —1 t— —1 S i , j — 1 S i , j S i , j + 1	S i t , j
	S i— 2 =1 (R 1 =30)	S i— 2 = 0 (R 2 =225 )
000	0	1
001	1	0
010	1	0
011	0	1
100	1	0
101	0	1
110	0	1
111	0	1

□ □□□□□□□ЕН□□□□□□□□□□□□□□□□□□

Fig.1. Performance of Reversible CA

An example of reversible CA with rule 30 is shown in Fig. 1. The first row is the input vector and the second row is repetition of first row. As shown in Fig. 1, the next state of cells is determined with two rows above this state. For reversibility of automata, the row at time (t-2) can be placed after row at time (t-1) and the rules of the reversible automata are applied according to Table 3. The reversible operation is applied and then the initial states is obtained. In Fig. 1, the reversible steps are shown in gray color.

• V.    Proposed Image Cryptography

The proposed method for image cryptography is based on reversible CA. In this method, two one-dimensional reversible CA and one elementary CA are used. The cryptography algorithm is described below:

Step 1: Two rows of input image are read and m (determined by user) number of pixels are selected from two rows. (In Table 2 m is set 2).

Step 2: These pixels in each row are placed in binary way according to its values.

Step 3: According to K that was determined by user binary string in step 2 is divided into k parts. (In table 2 with k=2 the string is divided in 2 parts.)

Step 4: Two produced binary strings are considered as input of reversible CA, and cryptography of numbers is performed by the CA. The output of this step consists of numbers in two times of t and (t-1).

Step 5: In step 4 substituted procedure is performed. Then, in this step the scrambling procedure is applied on the output of previous step by elementary CA for random value generation. Binary strings are connected to each other as output.

Step 6: Generated data in step 5 feeds as input of another reversible CA and encryption is done.

Step 7: In last step, two outputs are generated for two times of (t) and (t-1), which are the encrypted values of pixels. These values are stored in the encrypted matrix, as shown in Table 4.

In the decryption step, the above steps are applied reversely. Using the encrypted image and the key given as encrypted matrix in time (t-1), the image can be decrypted reversely according to the algorithm. One example of an iteration of 7 steps is shown in Table 4.

Table 4. Values of the Correlation of Cameraman with Rule 98.

Correlation	diagonal	vertical	horizontal
Original image	0.9373	0.9546	0.9562
[20]	0.0114	-0.0383	-0.0369
[21]	-0.0178	0.0149	0.0122
[22]	0.0068	-0.0176	-0.0116
[23]	0.0113	0.0337	-0..204
Proposed method	-0.000067	-0.0015	0.0012

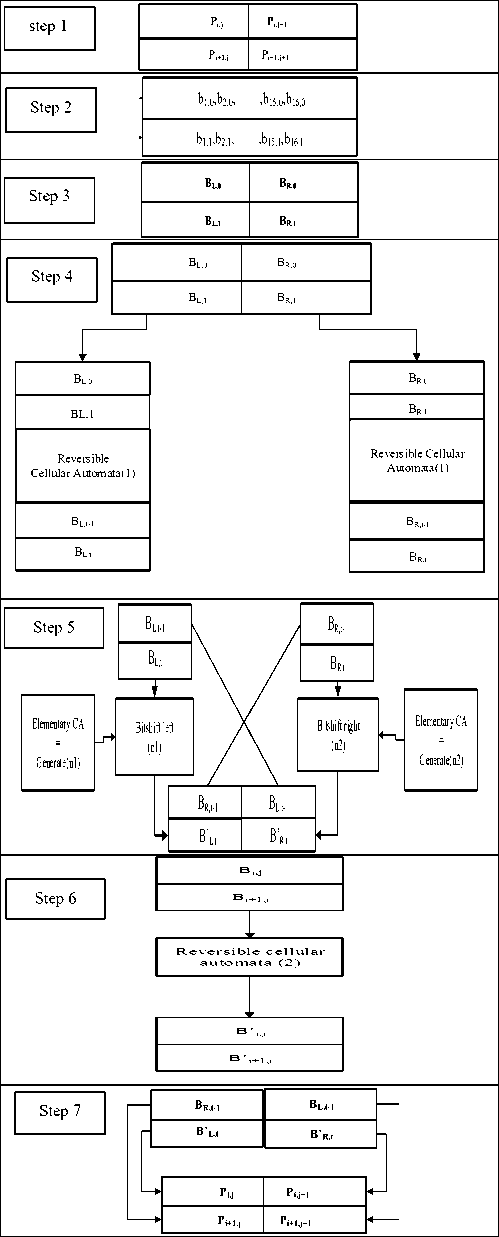
Fig.2. Proposed Method.

• VI.    Experimental Results

The results of implementation on cameraman and boats images at sizes of 256 × 256 with different keys are shown. Fig. 3 to 5 illustrate the original, encrypted and decrypted image of cameraman with rules 30, 98, and 153, respectively.

To illustrate the sensitivity of the algorithm to keys in Fig. 6, we tried to decrypt the encrypted image with rule 98 with another key. As it is seen, decryption was not done correctly and the image is completely inaccurate. In

Fig.7 to 9, this algorithm has been applied to the image of boats and the results are shown.

A. Original image.

B. Encrypted image.

C. Decrypted image.

• Fig.3.    Output Results of Proposed Algorithm With Rule 30.

  

  A. Original image

  
  
  

  B. Encrypted image.

  
  
  

  C. Decrypted image.

  
  

• Fig.4.    Output Results of Proposed Algorithm With Rule 98.

  

  A. Original image.

  
  
  

  B. Encrypted image.

  Fig.5. Output results of proposed algorithm with rule 153.

  
  
  

  C. Decrypted image.

  
  
  
  
  
  
  
  

• A.    Encrypted image with rule 98.

• B.    Decrypted image with rule 153.

  

  A. Original image.

  
  

  Fig.6. Output results of proposed algorithm with rule 98.

  

  B. Encrypted image.

  
  
  

  C. Decrypted image.

  
  
  

  A. Original image.

  
  

  Fig.7. Output results of proposed algorithm with rule 30.

  

  B. Encrypted image.

  
  
  

  C. Decrypted image.

  
  

• Fig.8.    Output results of proposed algorithm with rule 98.

  A. Original image.

  
  
  

  B. Encrypted image.

  
  
  

  C. Decrypted image.

  
  

• Fig.9.    Output results of proposed algorithm with rule 153.

• VII. Analysis and Evaluation of Proposed Method

In this paper, we examined the proposed scheme with [20-23]. In the following, you will see the evaluation of our method in comparison with those methods.

• A.    Statistical Analysis

According to Shannon's theory, attackers can decrypt encrypted image by using statistical analysis. The cryptography algorithm should be such that it will increase the difficulty of statistical analysis. Histogram analysis and correlation coefficients are used to evaluate statistical analysis [22].

A. Original image.

C. Encrypted image by rule 98.

D. Histogram.

0       50       100      150      200      250

F. Histogram.

C. Encrypted image by rule 153.

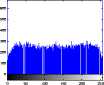
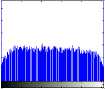
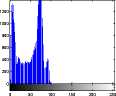
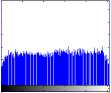
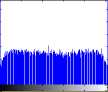
distribution of the pixels in the image by plotting the number of observations at brightness intensity.

Histogram of original and encrypted images of two cameraman and boats images is shown in Fig. 10 and Fig. 11, respectively. As seen in the figures, the histogram of the encrypted images is uniform and then it is suitable.

• 2.    Correlation coefficients analysis

Another evaluation criterion for statistical analysis is correlation. As the correlation of adjacent pixels in the encrypted image is less, the performance of the algorithm would be more suitable [22].

To evaluate the correlation of pixels in horizontal, vertical and diagonal direction, we use (1). In this equations, x and y are brightness of two adjacent pixels in image and N is the number of pixels selected from image. The values of the correlation in three vertical, horizontal and diagonal directions for the cameraman image and its encrypted images with rules 98 and 153 with four algorithms introduced by [20-23] and the proposed algorithm are shown in Tables 4 and 5, respectively. Based on values, as expected, the pixel correlation of the original image is high. In the encrypted images, this value is reduced and the pixels are less dependent on each other. In the proposed method, this value is less than the other methods, indicating that the proposed method has better performance than others.

cov( x , y )

D ( x ) D ( y )

Fig.10. Output Results of Proposed Algorithm with Rule 153.

1N cov(x, y) = — S(xj - E(x))(yj - E(y))      (2)

N j = 1

A. Original Image.

B. Histogram.

0        50       100      150      200      250

N

E ( x ) = ^ S x j              (3)

N j = 1

N

D ( x ) = n S ( x j - E ( x )) 2             (4)

N j = 1

C. Encrypted image by rule 98.

D. Histogram.

0        50       100      150      200      250

E. Encrypted image by rule 153.

F. Histogram.

Fig.11. Output Results of Proposed Algorithm With Rule 153.

1. Histogram analysis

A cryptography algorithm is suitable when the image is encrypted in a way that no information is seen from the original image. In other words, the image must not be visually recognizable in cryptography. As the result of the visual test varies from one viewer to another, a histogram analysis can be used. Histogram analysis describes the

Table 5. Values of the Correlation of Cameraman with Rule 153.

Correlation	diagonal	vertical	horizontal
Original image	0.9212	0.9536	0.9489
[20]	0.0410	-0.0641	-0.0632
[21]	0.0432	-0.0635	-0.0604
[22]	0.0017	-0.0227	-0.0219
[23]	0.1368	0.2562	0.1541
Proposed method	-0.0015	-0.0052	-0.0166

• B.    Sensitivity analysis

  An ideal property for an encrypted algorithm is sensitivity to small changes in the original image and keys. Three criteria of UACI, MAE, and NPCR are used to test the effect of changing an input pixel on the encrypted image. As these three criteria are higher, the cryptography algorithm would have more efficiency (Kanso and Ghebleh 2012).

Equation 5 introduced mean absolute error [1]. In this equation, C (i, j) and P (i, j) are the pixel values of the encrypted image and the original image, respectively.

Equation 6 shows the calculation of NPCR, which measures the percentage of different pixels between two cipher images whose plane images have only one pixel difference. C1 and C2 are two different cipher images whose corresponding plaintext images differ by only one bit [8,20].

The UACI is illustrated in 8. It measures the average intensity of differences between two cipher images.

Table 6 shows the values of the evaluation criteria for the algorithms introduced by [20-23] and proposed algorithm with rule 153. From table, we can see that the values for the proposed method have the highest value compared to others; that is, the tiny change of pixel in the original image causes great change in encrypted image.

Г 0 if C i ( i , j ) = C 2 ( i , j ) [ 1 if C i (i , j ) * C 2 ( i , j )

UACI =

NN

EE C i ( i , j ) - C ₂( i , j ) i       i = i j = i

M x N       255

Table 6. Values of the MAE, NPCR and UACI

Ref.	MAE	NPCR	UACI
[20]	39.572	49.3057	15.0151
[21]	38.6359	49.4232	13.8246
[22]	74.4251	49.2706	9.6542
[23]	40.8497	50.0253	15.0241
Proposed method	44.7147	50.2045	17.3348

C. Entropy analysis

Entropy is another important characteristics of the randomness of the algorithm. Entropy is calculated according to 9., where P(m i ) is the number of occurrences of m i . In an ideal state, for an encrypted image, which each pixel of it is 8 bits, this value should be about 8 [22]. Table 7 shows entropy values for mentioned methods.

NN

MAE = MN SEl C (i,j ) - P ( ' -Л-     (5)

i = 1 j = 1

2 ^N - 1

H ⁽ m ) = E ^{P (} m i ) ^X log 2

i = 0

1 P ( m_i )

NN

EE ^D ( i , J )

NPCR = — —----- .         (6)

M x N

Table 8. Key Sensitivity Analysis.

Original key		Slightly changed keys
Encrypted image	Histogram	Encrypted image	Histogram
	*■■		*111111
	i |MIII	SS8	*|i
	■B

Table 7. Values of Entropy.

Methods	Proposed method	[20]	[21]	[22]	[23]
Entropy	7.9892	7.9322	7.4259	7.2992	7.9253

• D.    Key sensitivity analysis

Key sensitivity is one of the essential characteristics for a cryptography algorithm. This means that changing a bit in the private key should produce a completely different encrypted image. The high sensitivity to the key guarantees the security of the cryptography system against Brute-force attack. To evaluate the characteristics of sensitivity to the key, the original image is encrypted with the one secret key, then, the key is slightly changed and the original image is re-encrypted. If the comparison of these two encrypted images is not possible visually, the encryption algorithm would have high sensitivity to the key.

Table 8 shows the result of the sensitivity to key test. In order to detect the difference of encrypted images, histogram of the images has been plotted to make their comparison easier.

• E.    Key space analysis

  In order to prevent brute-force attack, the key space of the cryptography algorithm should be large enough. The key space of the algorithm contains the total number of available keys in the cryptography algorithm. As the key space of cryptography is larger, the time to test all keys would increase, so it would be resistant to brute-force attack. In the proposed algorithm, four automata are used. Due to the fact that in each automaton, 2⁸ rules can be used, the key space is 2 8 x 2 8 x 2 8 x2⁸=2³ 2 =4294967296, so proposed structure is immune to brute-force attack.

• F.    Implementation analysis

The performance of a cryptography system is evaluated based on various factors such as reliability against various attacks, computational complexity and cryptography time. In the previous sections, it was observed that the proposed algorithm had a good performance against various attacks. In this section, computational complexity and algorithm implementation time are discussed. The proposed algorithm is performed in three steps and includes various operations, including production of random numbers, linear calculations of CA, shifting, and bit XOR. All of these operations have direct implementation. Therefore, the proposed algorithm is efficient computationally.

• VIII. Conclucion

CA is a useful tool for cryptography. Due to the randomness of the CA, the image can be encrypted with high quality. The reversible CA also has the capability to introduce reversible cryptography techniques on the image. The proposed method uses reversible CA to encrypt the image. In this article, a new structure for image cryptography is introduced, which encrypts the image in three steps. The results of the application of this algorithm on the image compared with the methods introduced in [20-23] by evaluation criteria such as UACI, MAE, and NPCR. The results show that this method has better performance.