A novel intelligent ARX-Laguerre distillation column estimation technique

Process industries, and the distillation column systems used within those industries, are significantly nonlinear which creates multiple challenges in system modeling, control, and fault detection. A block diagram of a distillation column, typical in the oil and gas industries, is shown in Fig. 1. In practical applications, the uncertain conditions surrounding distillation columns results in an increase in difficulty for system modeling, control, and fault identification. However, different types of modeling have been defined for nonlinear systems. These are usually divided into numerical-mathematical and physical-mathematical modeling [1-3], which are the two primary methods for mathematics-based system modeling [4, 5]. In practice, mathematical modeling of a distillation column is complicated due to its complexity and lack of information regarding various parameter values. To address mathematical modeling issues, a novel system identification technique is proposed.

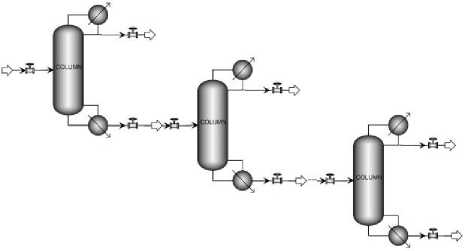
Fig.1. Continuous distillation column

There are a variety of techniques available for use in system identification, but they are primarily divided into two main groups: linear system identification techniques and nonlinear system identification techniques. Over the years, the availability of system identification techniques for modeling linear and nonlinear systems has increased. As shown in the literature [6, 7], linear and nonlinear identification techniques have been introduced for numerous types of systems. Linear modeling of linear and nonlinear systems by ARX techniques has been presented to reduce the complexity of operation parameters. The linear-ARX method has been used in various applications for system identification [6, 7] and fault detection [8]. While advantageous, drawbacks to the ARX method include difficulties modeling in the presence of a disturbance and/or external noise. In an attempt to solve this issue, the Laguerre filter has been used to reduce the effect of noise on the input and output [9]. As a result, the ARX-Laguerre method has been used for system identification in various applications including robot arms [10] and rolling bearing elements [11]. The primary drawback of this technique is system estimation in highly nonlinear and uncertain systems. To improve on these drawbacks, an intelligent ARX-Laguerre technique is recommended. For the first time, a nonlinear-ARX system identification method was introduced by Billings in 1980 for nonlinear-discrete system modeling [12]. Different techniques can be introduced for nonlinear-

ARX system modeling, such as block-structured system modeling [13], neural network-based system modeling [14], and Volterra series system modeling [15]. Nonlinear-ARX system modeling has been used for the modeling of several real systems, including an aluminum plate [16], wind turbine [17], and bearing systems [18, 19]. In real-world applications, the impact of noise plays a significant role in accurate system estimation. Several researchers have introduced methods for the removal of signal noising. The ARX-Laguerre technique is a dominant method for system identification in the presence of noise and unknown conditions, and is used to reduce the model estimation complexity despite unknown conditions [20].

An intelligent ARX-Laguerre system estimation is proposed in this paper to model a distillation column, based on adaptive techniques. In the proposed method, the ARX-Laguerre parameters are modified by an adaptive artificial intelligence technique. The accuracy of the system identification is verified by ARX and ARX-Laguerre techniques, with application to a distillation column. This paper has been divided into the following sections: Section two contains the related works, while the paper challenge and the proposed method objectives will be presented in Section 3. Section 4 provides the intelligent ARX-Laguerre estimation and analysis of the distillation column, results, and discussion. Section 5 concludes this paper.

• II.    Related Works

Modeling and estimation of industrial systems are significant topics of research in recent years. The distillation column is a nonlinear system, and its complexity increases when used in industry [21]. The subspace identification algorithm for distillation columns was introduced in [22]. This technique is linear, and can be useful for distillation columns with limited uncertainties. A comparative study between two types of linear system estimations, with application to the industrial electric motor, has been introduced in [6]. These two methods demonstrated acceptable performance for this system, but in the presence of noise, these two methods must be reevaluated. Li et al. [23] introduced a nonparametric method for modeling and estimation of nonlinear systems. The neural network method was recommended for analysis in that publication due to the robustness of the artificial neural network (ANN). There are various advantages to the conventional neural network technique, but the heavy computation load is a significant drawback to this technique. To improve on classical ANN, the gradient descent algorithm has been recommended to increase the system performance [24]. Further techniques, such as genetic algorithm (GA) and partial swarm optimization (PSO) have been introduced recently to improve the performance of ANN and reduce its computation load. The intelligent ARX technique has been introduced in [25], where the performance was improved by ANN and PSO. The main challenge in the use of this method is a lack of robustness. The ARX-

Laguerre method for fault identification and system estimation is introduced in [10, 11]. Here, the ARX-Laguerre method has been used for robot manipulator estimation [10] and bearing estimation [11]. However, these methods decrease the system performance in highly nonlinear systems.

• III.    Problem Statement

The distillation column is a nonlinear system with unknown parameters. Therefore, accurate mathematical modeling in this system in the presence of uncertainty and unknown inputs is complicated. Based on [20, 26], the system’s process information is listed in Table 1. Dynamic formulation of the distillation column in the presence of uncertainty is considered using the following formulations [1]:

Y 1 = [ Y 2 W V + U J W V

Y 2 = [ Y_XW V + U 2 W

V m

WiV

' wV v 0

W ^J

( )

W V '

0 ,

where Y , U , W are output, input, and state, respectively. In a distillation column, the system inputs are heat ( E ) , the rate of reflux ratio (e ) and the state, defined by ( M ) . Therefore, the system dynamics can be arranged as follows:

Y 1

Y 2

M_u M ₁₂ De .M 21 M 22 £ DE

Referring to [20], the transfer function for the proposed distillation column is presented below,

" -1248 140         " Y1 Y2 = 1 + 6.9 S -1590 (1 +1.26 S )(1 +1.58 S) 344 De DE (3) .1 + 2.9 S 1 +1.69 S      _ where Y ,Y are the differences in the two product temperatures, respectively. The frequency domain response of the distillation column is shown in Fig. 2. Based on Fig. 2, the primary harmonics in this system are

13.7( a ) and 15.7( a ) . However, based on [20], the sec            sec

system’s transfer function can be extracted from the distillation column but this scenario is very complicated. To reduce the complexity, we propose a new method.

Table 1. Distillation Column Specifications [26]

Specification	Value
Feed specifications
Feed flow rate	10 L/min
Feed composition	25 ethanol, 75 water, mol%
Reflux flow rate	0.6 L/min
Feed temperature	65 °C
Feed pressure	1 atm
Reflux ratio	2.5 molar
Column specifications
Column height	5.5 m
Distillate flow rate	2.5 L/min
Colum diameter	0.15 m
Type of tray	Bubble cap tray
No. of trays	15-plates
Tray spacing	Approx. 35 cm
Holdup	50% for 10 min
Top temperature	83.43 °C
Bottom temperature	92.75 °C
Reboiler duty	183.3 kW
Condenser duty	- 167.8 °C
Column pressure	1 atm
Distillate composition	85 ethanol, 16 water, mol%
Bottom composition	17 ethanol, 83 water, mol %

This paper introduces the following problems, as well as brief solutions.

Problem 1: Extracting the dynamic, accurate mathematical formulation of the distillation column is complicated.

Solution 1: The ARX identification technique is recommended for system estimation based on the input/output signals.

Problem 2: In the presence of external disturbances, the accuracy of the ARX estimation technique can be reduced.

Solution 2: The ARX-Laguerre technique is recommended for removing noise from the signal input and output.

Problem 3: System complexity is reduced using the ARX-Laguerre technique when compared to the ARX technique, but the system complexity is still high.

Solution 3: To solve this challenge, this research introduces an intelligence-based ARX-Laguerre method .

ARX System Estimation: An extensive variety of distillation columns can be specified using ARX techniques [27]:

Q ( к ) + ^ Q (к —1) + ^ Q ( к - 2) +... + Q( (к — n q ) =

£ 1 1 (к — 1) + 6 *2 1 (к — 2) +... + ^ i I (к — n i ) + e ( к )

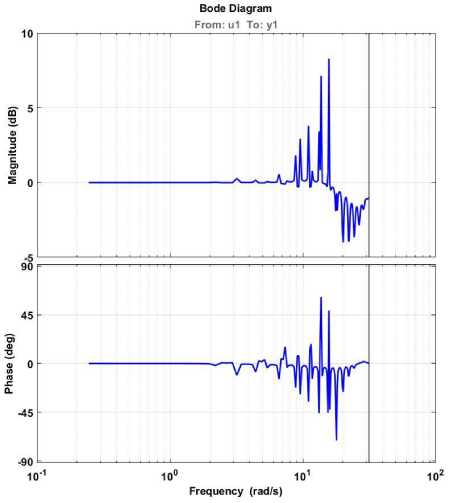
Fig.2. Frequency domain response

Based on (4), the future output can be predicted by using previous observation parameters,

Q ( к ) = —£ 1Q (к — 1) —... — £ qQ (к — n q ) + £ 1 1 (к — 1) + ... + £ i I (к — n i ) + e ( к )

where ( Q ( к — n_q ), I ( к — n i )), Q ( к ), I ( к ), (L, £ * ), е ( к ) are the systems lag, output, input, unknown parameters, and zero-mean noise, respectively. The state-space system is defined as follows:

Q ( к ) = — ^ ( к ). ^ + e ( к )

<_z = [^... q_q   £ 1 ...   6 ]                                         (6)

^ = [ — Q ( к — 1)...   — Q ( к — n _w )   I ( к — 1)...   I ( к — n i )]

Here, ^ is a regressor variable of ARX modeling and x is the unknown parameters matrix. According to (5) and (6) the ARX system estimation is defined as (7).

• IV.    Proposed Methodology

To effectively model the distillation column using a signal-based system identification technique, an adaptive intelligence-based ARX-Laguerre technique is recommended. In the first step, system modeling based on the ARX method is proposed.

Q ( к ) = 5 [ Q ( к —1), Q ( к —2),..., Q ( к — n_w ) , I ( к —1), I ( к —2),..., I ( к — n i )]

The least-squares technique has been defined to estimate and predict the best value for 5 .

О * = arg min у { f (0 , d)}

1 ^k

f ^{( 0} ,^{d )} =   2 ⁽ Q ^(к ) ^- ^ ^{( к )} X ^{) 2}

k ₀

Fig. 3 illustrates the estimation performance for the distillation column based on the ARX techniques. According to the figure, the fit criterion for ARX is about 74.2% for this system.

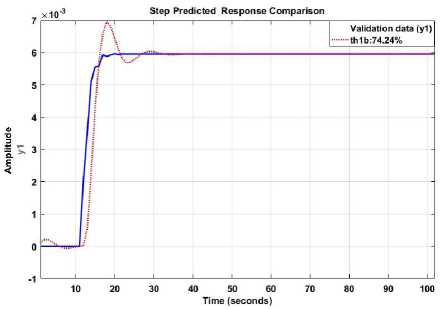
Fig.3. Fifth order ARX estimation with application to a distillation column

After system estimation using the ARX technique, an alternate technique can be used for system modeling, such as an IDPOLY, Z-transform, state-space, or transfer function. In this paper, transfer function system modeling is used for both modeling and analysis. The discrete time ARX model is calculated as follows:

A ( z ) F ( t ) = B ( z )U ( t ) + e ( t )

A ( z ) = 1 + Z ^{- 1} + 6 Z ^{- 2} + Z ^{- 3} - 3 Z - 4 - 7 Z "5        (9)

B ( z ) = -0.3 - 0.8 Z ^{- 1} - 3 Z "² - 6 Z ^{- 3} - 7 Z - 4

Based on Fig. 3 and (9), the transfer function of the ARX model is obtained by the following:

where S ( k ),( A , b i , a ), Q ( k ), I ( k ), A d ( k ) are the state of the system, unknown parameters, output, input, and system uncertainty, respectively. Regarding (10), the future state and current output of the system depend on two factors: current states and current input. To improve accuracy, performance, and to reduce the system’s estimation order, the ARX-Laguerre technique is proposed,

N a - ¹       ™   1 - Z

Q ( к ) = 2 K n , a ( 2 '   \ (^- ) ⁿ * Q ( к ))

0        j=1 Z Za Z Za у1 K /у V1 -Z ^-Tsiz*

. S n , q ^{( к} ) ⁺     K n , в ⁽     7       ⁽ 7        )

0        j = 1 Z ^- Ч р Z ^- 4 p

I ( к )). S n , I ( к )

where   ⁽ K n, a &  K n , p )   ,   ⁽ N a &  N e )   ’*’   ^S n , q ⁽ k )

17 ^ 2     2 n    1 - ^5 1 - £ >, zⁿ

S(k)  , ((a .  5“’  ),e / . —e—)) are the Fourier z - 5a z - 5a    z - 5p z - 5p coefficients, system order, convolution product, filterbased input signal, state signal, and Lagrange base function, respectively. According to (12), the state-space equation for the ARX-Laguerre system estimation is proposed as follows.

<

S ( к + 1) = [ AS ( к ) + bl ( к ) + b q Q ( к )] + A d ( к )]

i                q                    (13)

[ Q ( к ) = ( a ) T S ( к )

Based on (12), the future state in the ARX-Laguerre system estimation technique is related to the current state, input, and output. This technique reduces the system’s order estimation. Fig. 4 demonstrates the estimation accuracy for modeling based on the ARX-Laguerre method. Based on Fig. 4 and (13), the system estimation for the proposed system is calculated as follows:

| S ( к +1) = [ AS ( к ) + b i I ( к ) + b q Q ( к )] + A d (к )]

[ Q ( к ) = ( a ) T S ( к )

-0.3S4 - 0.8S3 - 3S2 - 6S - 7

S ⁵ + S ⁴ + 6 S ³ + S ² - 3 S - 7

A =

-1.87

-1

, ^bi =

1 ’

b_q = [ 0.015  0.26 ]

Based on (10), this system is modeled by a 5th order equation. The classical ARX technique has two significant drawbacks: the estimation accuracy (74.24%) and the high system estimation order (5th order), causing highly nonlinear behavior. To address these issues, the ARX-Laguerre method is introduced in the next step.

ARX-Laguerre System Estimation: The state-space function based on ARX system estimation is calculated as follows:

S ( к +1) = [ AS ( к ) + b i I ( к )] + A d ( к )] <

Q ( к ) = ( a ) T S ( к )

a = [ 0.025 0.26 ]

Based on (14), the transfer function for ARX-Laguerre distillation column estimation is calculated as follows:

0.2 S + 0.4

^H 9

S ² + 0.5 S + 0.4

Regarding Figure 4, the fit criterion for the ARX-Laguerre system is shown to be approximately 80%. To further improve the performance of ARX and ARX-Laguerre system estimations, the AI-ARX-Laguerre method is proposed.

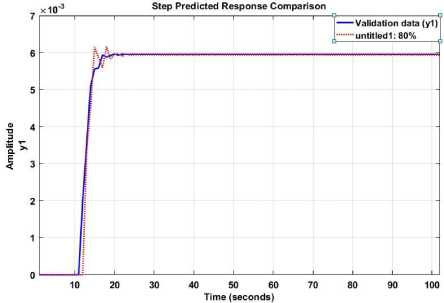
Fig.4. Second order ARX-Laguerre estimation with application to a distillation column

Q ( к ) = [Ф_ь Ф ₂ ,..., Ф, ] x [Ц, Q 2 ,..., Q ]       (20)

Therefore, based on (19) and (20), the Schmidt’s orthogonal formulation is expressed as

Q ( k ) = ФxQ = ^xn

9 =Ф»

( nn + rr )!  ^

(^" (Ф> ,9^ h = 1     (⁹rr ’ ⁹ rr)

_n = QQ 9

(9,9

AI ARX-Laguerre System Estimation: The ARX-Laguerre technique reduced the ARX system order from 5th to 2nd order, and increased the fit criterion from 74.24% to 80%. To increase the system’s modeling performance, the AI ARX-Laguerre technique is introduced here. The intelligent function is defined in the following equation, where 9,(nn, rr)n are the orthogonal matrix, function order, and coefficient term, respectively. The error value is given as

Err =

( n )² ( 9 , 9

r_LL1211J0% x100%

Q , Q

Q (к) = f_Ai [ Q (к -1), Q (к - 2),..., Q (к - n q )

, 1 ( к -1), 1 ( к - 2),..., 1 ( к - n )]                    ⁽¹⁶⁾

Therefore, based on (21), the model structure is satisfied if we introduce the following condition:

where f_AI is a nonlinear function for system estimation, defined by the intelligent technique. The nonlinear intelligent function, f_AI , is calculated using the following equation:

( nn + rr )! ( rr !)( nn !)

¹ -   £   ^{{ Err} }< ⁸

h = 1

n

Q (к) = Qo + ^Д(к) + it=1

nn

^Х^ЛЛЛ) V к +...

i г 1 = 1 г' i = 1

where 8 is a threshold value. Referring to (19) and (23), the orthogonal nonlinear ARX-Laguerre model is written as follows:

where   Q i is the coefficient for system modeling,

n = n_q + n i and S i ( к ) is:

( n' n '+ r ’r ')!

( r'r '!)( n' n ‘ !)

Q n ( к ) =   £   9 Ф. ( к ) ^

Й ‘ h '= 1

( n' n '+ r'r ')!

( r'r '!)( n' n '!)

^Qn ^{( к )} =   £   9^г ^{( к )}

Й ‘ h '= 1

S i ( к ) =

Q ( к -ii )

^{1 (к -} (ii ^- n q )

1 < ii < nn q nn +1 < 1 < nn + n,. q     qi

where,

Therefore, based on the (17) and (18) we have

( n' n '+ r 'r ')!

( r'r '!)( n' n '!)

^ = ^{Ф -} £

Й= rr +1

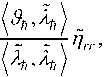
( nn + rr )!

( rr !)( nn !)

^{Q ( к )} =   £ X Ф ^{( к )} ,         (19)

К = 1

where x is the coefficient of system modeling, and Ф^, ( k ) is a regression term. The orthogonalization model is calculated as the follows:

To validate the model, different techniques have been used, such as the one step ahead method and model predicted output technique. Based on the one step ahead technique, the AI ARX-Laguerre technique is defined as follows:

Q ( к ) = aQ ( к -1) + a 2 Q ( к - 2) + ci (к -1) 1 ( к -1)

where a , a , and c are output/input system order coefficients. Thus, the model prediction is given as:

Q ^ˆ (3)= a 1 Q (2)+ a 2 Q (1)+ cI (2) Q (2)        (27)

The system prediction frequency response is illustrated in Fig. 5.

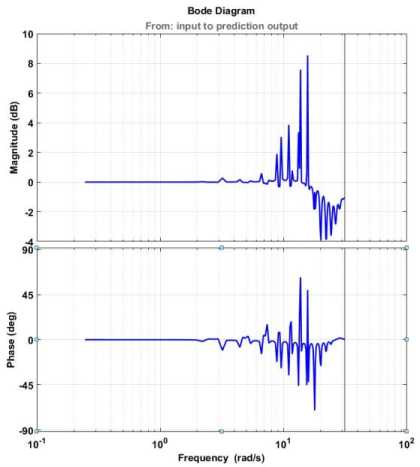
Fig.5. System prediction frequency domain response for the AI ARX-Laguerre technique

Based on Fig. 5, the primary harmonics in this system

Rad        Rad are 13.7(    ) and 15.7(    ) . Based on a comparison sec             sec

between Fig. 2 and Fig. 5, it is clear that one step can accurately predict the frequency response of the AI-ARX-Laguerre model ahead technique. The block diagram of system estimation based on the AI ARX Laguerre technique is illustrated in Fig.6.

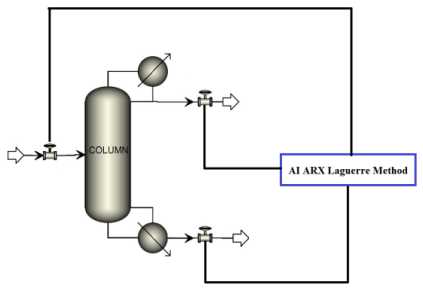
Fig.6. Block diagram of proposed AI ARX-Laguerre distillation column estimation

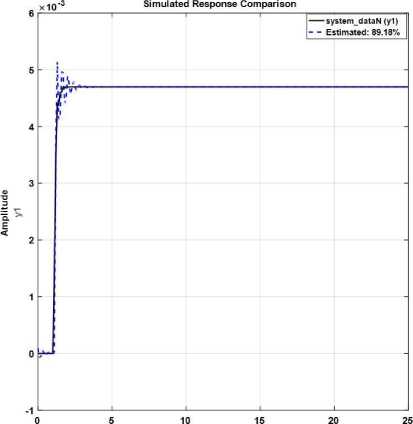
Fig. 7 illustrates the real step response and identified system response based on the AI ARX-Laguerre system identification technique. Regarding this figure, the system identification accuracy is approximately 89.2%. Based on this method, the discrete AI ARX-Laguerre model for the distillation column is identified as:

Γ( z ) Q ^ˆ ( κ )=Π( z ) I ( κ -1)+ e ( κ -1)

Γ( z )=1+0.1717 Z ^{- 1}+0.6374 Z ^{- 2}          (28)

Π( z ) = 1.449 Z ^{- 1}+0.3594 Z ^{- 2}

The root mean square error (RSME) is given as:

RMSE =

NN

∑ ( Q ˆ rr - Q rr )² rr = 1

NN

Based on (28) and (29), the root mean square error is 6.588 × 10 ^{- 9} .

Time (seconds)

Fig.7. AI ARX-Laguerre distillation column identification technique

The distillation column estimated by the AI ARX-Laguerre technique is modelled based on (30).

Q(κ)=∑χ ΦК (κ) → h ′=1

Q ( κ ) = 0.7986 Q ( κ -1)+0.232 Q ( κ -2)

+0.0127 Q ( κ -3)-0.0496 Q ( κ -6)-           (30)

3.14×10 ^{- 4} I ( κ -1)+7.517×10 ^{- 4} I ( κ -2)+

4.92×10 ^{- 4} I ( κ -5)+0.3947 Q ( κ -1) I ( κ -1)+

0.2564 Q ( κ -2) I ( κ -5)

Based on (30), the ARX-Laguerre transfer function is calculated as follows:

14.77 S +309.4

S ² +11.24 S +309.4

The transfer function identification accuracy is represented in Fig.8. Regarding this figure, the accuracy rate is more than 91%. Fig. 9 depicts the impulse response for distillation column identification by the AI ARX-Laguerre approach.

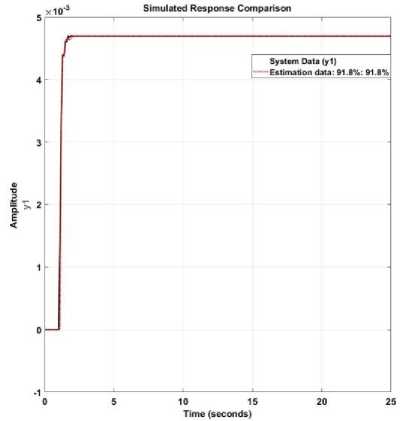
Fig.8. Continuous time identified transfer function by the AI-ARX-Laguerre distillation column identification technique

	" 0.8	0.2	0.01	0.05	0.06	- 0.05	- 0.01	0.006
	- 0.3	0.5	0.2	- 0.3	0.2	0.23	- 0.003	0.05
	- 0.2	0.2	0.1	- 0.7	- 0.1	- 0.2	- 0.02	- 0.04
h 11 =	0.04	0.2	0.9	0.3	- 0.4	0.05	0.03	- 0.02
	- 0.2	- 0.8	0.8	0.02	0.7	- 0.2	- 0.02	0
	0.1	- 0.5	0	0.3	- 0.6	- 0.08	- 0.3	0.2
	0.03	- 0.2	0.2	- 0.1	0.2	0.4	- 0.8	- 0.5
	- 0.3	0.2	- 0.4	0.3	- 0.4	0.5	0.15	0.02

⁽ h i2 + h 21 ) =

-3.14 x10 9 7.52 x10 9 -4.93 x10⁹ 9.74 x10⁹ 4.92 x10⁹ -9.35 x10⁹ 5.22 x10⁹ 1.12x10⁹

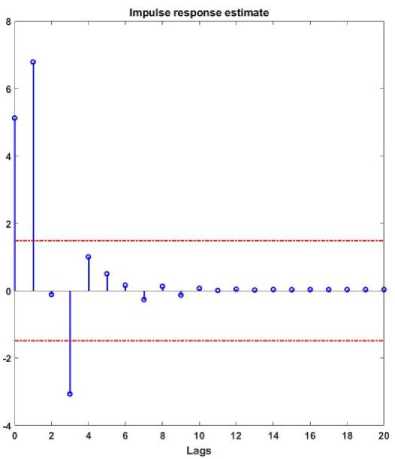
Fig.9. Estimated impulse response by the AI-ARX-Laguerre distillation column identification technique

The discrete time state-space model estimation based on the AI-ARX-Laguerre technique can be identified as

h = 22	-1.8 x10 " 10 5.6 x10 - 11 -4.4xl0 '' 1.5 x10 11	T
	-5.3 x10 - 12 8.1x10 12 -1.7 x10 - 12 3 x10 - 12 h 23 = [ 0 ] -9.53 x108 9.57 x108 -4.19 x108 1.3 x109	(35) (36)
K 11 =	-1.6 x109 5.75 x106 -3.83 x109 2.8 x109	(37)

5 ( t + T s ) = h_n. S ( t ) + h i2 . I ( t ) + h 21 Q ( t ) + K 11 . e ( t )

Q ( t ) = h 22 . S ( t ) + h 23 . I ( t ) + e ( t )                            ⁽   )

where   hn,( h12 + h21), K11, h2 2, h2 3  are calculated as follows, respectively.

• V.    Conclusion

Mathematical models are pivotal in the analysis and design of distillation columns, but accurate modeling of the physical system is complex. Therefore, in this research, the artificial intelligence based-ARX-Laguerre method was introduced for distillation column modeling. The results indicate that the proposed method can improve the performance and accuracy of nonlinear distillation column modeling. Compared with ARX and ARX-Laguerre system estimations, the proposed method demonstrated improved reliability in time and frequency response. Furthermore, this technique provides a reliable model for system control, system analysis, and fault diagnosis of the distillation column.

Acknowledgment

This work was supported by Research Fund of University of Ulsan.