A Novel Method for Grayscale Image Segmentation by Using GIT-PCANN

Image segmentation, which an image is partitioned into separate parts, normally two parts corresponding to the background and the foreground, is an important process for content analysis and image understanding [1]. Many researches have been done in creating different segmentation methods but there is so far no a method can be effective for all types of image segmentation problems.

Pulse-coupled Neural Network (PCNN)based on the phenomena of synchronous pulse firing in the visual cortex of cat, has been widely applied for image segmentation because of its biological vision advantages[2-12]. The existing segmentation algorithms based on PCNN exhibits some disadvantages: (1) some algorithms requires multiple PCNN parameters and a satisfactory result strongly depends on the parameters and there is so far no mathematical theory to explain the relations of segmentation results and parameters selections. (2) The segmentation result is closely related to the PCNN iteration times. And (3) traditional PCNN threshold is a time decaying value and it is not related to the grayscale statistics of the image, which is a significant factor for image segmentation.

In this paper, a new method, called grayscale iteration threshold pulse coupled neural network (GIT-PCNN), was proposed for image segmentation, which integrates grayscale iteration threshold with PCNN. PCNN has been widely used in image segmentation. However, satisfactory results are usually obtained at the expense of timeconsuming selection of PCNN parameters and the number of iterations. In this method, traditional PCNN is simplified so that there is only one parameter to be determined. Furthermore, the PCNN threshold is determined iteratively by the grayscale of the original image so the image is segmented through one time of firing process and no iteration or specific rule is needed as the iteration stop condition. So the PCNN threshold is related to the grayscale statistics of the original image. The method demonstrates better performance and faster processing speed compared to those PCNN based segmentation algorithms which require the number of iterations and image entropy as iteration stop condition. Experimental results show the effectiveness of the proposed method.

The remainder of this paper is organized as follows. Section II introduces the proposed GIT-PCNN model. Section III presents the detailed implementation of the GIT-PCNN, and chooses suitable parameters for the proposed PCNN. Section IV demonstrates experimental results and comparisons. Finally, some conclusions are drawn in Section V.

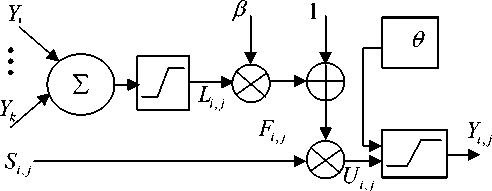
Figure 1 the simplified PCNN model of neuron N _{i , j}

Manuscript received April 25, 2011; revised June 23, 2011; accepted May 18, 2011.

• II.    Gray scale iteration PCNN Model and

Theory

• A. Simplified Pulse-coupled neural network

The simplified PCNN model of neuron ( i , j ) shows in Fig. 1.

where F ( i , j ) is the feeding, S ( i , j ) is the input impulse signal, в is the linking constant, L ( i , j ) is the linking, 9 (i , j ) is the dynamic threshold, Y ( i , j ) is the pulse output, and U ( i , j )is the internal activity.

The feeding accepts the original image grayscale:

F. j ( n ) = S ij                         (1)

Each neuron is connected with the linking neurons. The linking output is based on the status of the neurons in the linking field. The linking output is 1 if at least one neuron fire in the linking field or 0 if no neuron fires.

L i , j ( n ) = step ( £ WY ( ⁿ - 1)) = * k e G

1,

0,

if E WY ( n — 1)) >  0

keG else

where G is the linking matrix of neuron N_{i , j} , which can be 3 x 3 or 4 x 4 linking field. Fig 2 shows a 3 x 3 linking field.

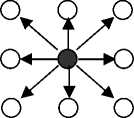
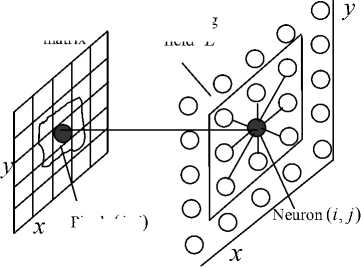
Figure 2. 3 x 3 linking field network when PCNN is used for segmentation purpose, shown in fig.3.

PCNN

Linking field L

Image pixel matrix

Pixel ( i , j )

Figure 3. PCNN segmentation model

When в = 0 , neurons are independent and without link. Assume the initial threshold 9 (0) = 0 , then the feeding input of neuron N i j is F j (0) = S i j , which is the grayscale value of the original image. According to definition of Equ. (5), U (0) - 9 (0) = S - 0 >  0 , indicating all the neurons fire at time 0. After neurons fire the threshold is added with V T , if V T >  S i j then all the neurons do not fire, the output Y (1) = 0 . The output of neuron N ij remains to be 0 until the threshold function is decayed to 9 _ij ( k ) <  S ij at time k , then neurons fire again. The natural firing process of neurons is periodic, shown in fig. 4. The PCNN output firing pulse Y_{i , j} ( n ) with fixed frequency, which higher intensity corresponds to higher firing frequency. Neurons with same intensity fire at the same time, in contrast neurons with different intensity fire has different firing time.

The linking inputs are biased and then multiplied with the feeding input to form the internal activity U ( i , j ).

U ,.j ( n ) = F i j n )(1 + p L ij ( n ))          (3)

The threshold of all neurons is the same, whose value is the iteration grayscale level of the original image.

• 9.A n ) = 9 .                           (4)

The pulse generator of the neuron consists of a stepfunction generator and a threshold signal generator. At each firing step, the neuron output Y ( i , j )is set to 1 when the internal activity U ( i , j )is greater than the threshold function 9 (i , j ) and then the threshold is updated consequently, otherwise the output Y ( i , j )is set to 0.

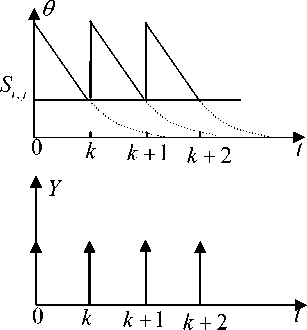
Figure 4. the natural firing process of neuron N_{i , j}

[ 1, u ( n ) >  9 ,( n )

Y j n ) = Step [ U ij ( n ) - 9 j ( n )] = j ¹ ,^л i , ^jV (5) [ 0, otherwise

When в * 0 , the neuron N i , j with highest intensity fires at time t , then the neuron N_{m , n} in the neighboring field of N_{i , j} is captured by N_{i , j} . Thus the internal status of N_{m , n} which is F_{m , n} is changed to F m (1 ⁺ P L mn ) . Assume F m , n <  ⁹ m , n but

^F m , n ⁽¹ + ^ L m , n ) >  ⁹ m , n then the unfired neuron ^N„ is captured by the fired neuron N_{i , j} and fires at time t prior to the natural firing time, shown as fig. 5.

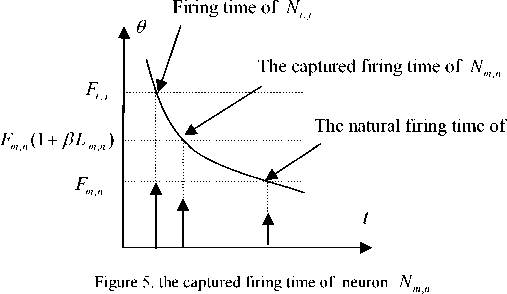
^{If F} mn <  ⁹ mn and ^F mn (1 ⁺ P ^L mn ) <  ^n it indicates that the intensity of neuron N_{m , n} greatly varies with that of neuron N_{i j} thus neuron N_{m n} can not be captured by neuron N_{i j} . Therefore t he pulse capture characteristics

9 = ( A 1 + A 2 )/2, k >  0

Segment the image with the new threshold until the iteration time reaches a predefined value.

During the firing procedure the neurons whose intensity value is greater than the threshold fire first. Simultaneously the firing neurons begin to communicate with their neighbors. The result is an auto-wave that extends from an active pixel to the whole region. So the output of every neuron affects the output of its neighbors affected by the others at the same time. The Nm n    y value of each pixel and the status of its neighbors or inactive) determine what time a neuron fires.

Neurons in the same region or with an approximate F value tend to fire at the same time. When there are pixels whose intensity value are approximate in its neighboring region the pulse output of one of them will fire the others in the specified neighboring region and then produce a pulse output sequence Y ( n ) . Obviously the firing matrix of PCNN contains two values 0 or 1 which corresponds to a black and white segmentation of the original image and the firing matrix includes the information of the image intensity distribution as well as the geometry of the original image which makes image segmentation reasonable.

of PCNN determines that the neurons spatially connected and intensity correlated tend to pulse together thus each contiguous set of synchronously pulsing neurons indicates a coherent structure of the image which make image segmentation by using PCNN is theoretical correct.

• C.    Grayscale iteration threshold

A threshold based on the images grayscale statistics is applied to partition an image into two parts:

I a ₀

g ⁽ x yy ) = 1

[ a

I(х,У ) ^ T I ( x , У ) > T

• D.    The algorithm implementation of GIT-PCNN

step 1: Select the average of the maximum and minimum intensity of the original image as the initial threshold, calculated as { 9 ^k } = ( I _max + 1 _min) / 2, k = 0 ;

step 2: split the image as two parts R ₁ and R ₂

based on the threshold of 9 ^k   , which

R = { I ( x , y ), I ( x , y ) >  9 }

R 2 = { I ( x , y ), I ( x , y ) <  9 }, k >  0 ;

step 3: Compute the mean grayscale of area R ₁ and

The image is partitioned as a black and white image when a ₀ = 0, a 1 = 1 . A proper threshold is the key of image segmentation.

The grayscale iteration threshold is applied, which the iteration starts with an approximate grayscale level.

R 2

A i =

9 } = ( I max + 1 m. )/2, к = 0           (7)

Where I and I are the maximum and minimum max          min grayscale level of the original image, respectively. The iteration begins with the average of the maximum and minimum grayscale value of the original image. The original image is partitioned into two parts, background and foreground based on the threshold.

R = { I ( x , y ), I ( x , y ) >  9 ^k }, k >  0      (8)

R 2 = { I ( x , У ), I ( x , У ) <  9 ^k }, k >  0       (9)

Calculate the average grayscale level of the background R ₁ and the foreground R ₂ as A ₁ and A ₂ . The threshold is updated as the average of A ₁ and A ₂ .

represented as A ₁   and A ₂ , respectively by

Z I ^{( x} , y )

I ⁽ x , y ) e R 1

Z C ( x , y )

I ⁽ x , y ) e ^R 1

Z C ^{( x} , y )

I ⁽ x , y ) e R 1

and

and Z

I ⁽ x , y ) e ^R 2

Z I ^{( x} , y )

I ⁽ x , y ) e ^R - 2

Z C ( x , y )

I ⁽ x , y ) e ^R г

, where

C ( x , y ) represent the pixel

number in area R ₁ and R ₂ , respectively;

Step 4: Calculate the new threshold ^ = ( A 1 + A 2 )/2, k >  0 ;

Step 5: If 0 ^k = 0 ^{k - 1} or abs( ^ k - 0 ^{k - 1} ) < the specified threshold then output threshold 9 , to step 6, otherwise, k = k + 1 , back to step 2, where abs represents absolute function;

Step 6: input the image normalized to [0,1] into the

feeding field F , initialize L = U = Y = 0 , в = 0.2 ;

Step 7: L = step (     Z     W_kY )

k e 3 x 3 neighbouring

Step 8: temp = Y ,

U = F .* (1 + P L ) , Y = step(U - 0 ) , where temp is a temporal matrix for saving result;

Step 9: if Y = temp output binary matrix Y which is the segmentation result ;

Step 10: otherwise L = step( ^ WkY) , back to k g3x3^M step 8.

• III.    Experiment Results

A set of images are used to test the effectiveness of the h-PCNN segmentation algorithm in the experiment.

• A.    Objective segmentation performance

  

  (a)                                       (_b)

  
  
  

  (c)

  
  
  

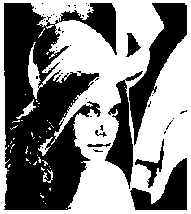
  (d)

  Figure 3 segmentation results (a) original Lena image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN

  
  

Fig. 3 shows the segmentation results of Lena image partitioned by three methods. (a) is the original image, (b), (c) and (d) are the segmentation results obtained by using methods in [11], [12] and the proposed GIT-PCNN, respectively. (c) has more details in the hair but the face organs are obscure. (b) and (d) have no much difference in objective vision.

(a)

(b)

Figure 4 segmentation results (a) original Cameraman image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN

(d)

Fig. 4 shows the segmentation results of Cameraman image partitioned by three methods.(a), (b) and (c) represent the original image, the segmentation results obtained by using methods in [11], [12] and the proposed GIT-PCNN, respectively. (b) provides much details on the background and is over-segmented, but presents shadow on the foreground face. The method in [12] illustrates block effect, which the bottom right block is oversegmented and provides too much details while the bottom left block is ill-segmented and obscure details, furthermore the segmented result contains noise. Relatively, the proposed GIT-PCNN segment foreground from background and provides clear foreground.

(c)

(d)

Figure 5 segmentation results (a) original Coins image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN

Fig. 5 shows the segmentation results of Coins image. (a) is the original image, (b), (c) and (d) are the segmentation results obtained by using methods in [11], [12] and the proposed GIT-PCNN, respectively. (b) and (c) have noise in the segmentation results but the image is effectively partitioned into two parts in (d).

(a)

(b)

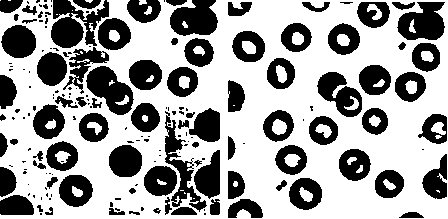
(d)

(c)

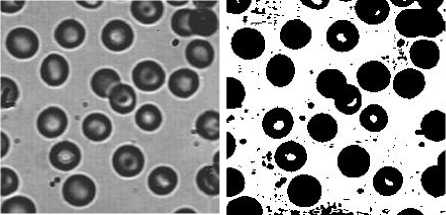
Figure 6 segmentation results (a) original Blood image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN

Fig. 6 shows the segmentation results of Blood image. (a) is the original image, (b), (c) and (d) are the segmentation results obtained by using methods in [11], [12] and the proposed GIT-PCNN, respectively. There is noise in (b). In (c), the segmentation result demonstrates block effect, which some blocks partition the image effectively but some blocks show over-segmentation or under-segmentation. GIT-PCNN can correctly segment the original image into two parts.

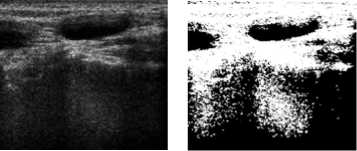
(a)                                (b)

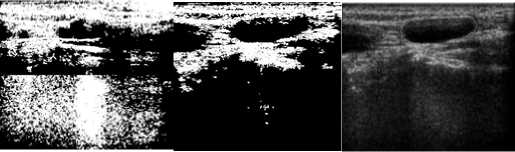
(c)                            (d)                              (e)

Figure 7 segmentation results (a) original ultrasound lymphonodus image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN (e) the edge segmented by professional doctor

The ultrasound imaging technology can display the organs scanned by the high frame frequency in real time. It is widely used in medical diagnosis because of its non-

invasiveness and low cost, but the image contains artifacts and much noise, which makes the further process difficult. Therefore an ultrasound image is chosen to segment by the proposed GIT-PCNN to demonstrate its effectiveness. Fig. 7 illustrates the segmentation results of an inflammatory ultrasound lymphonodus image by using methods in [11] (b), [12] (c) and the proposed GIT-PCNN (d). The purpose of segmentation is to separate the inflammation part from the normal organ. (e) is the inflammation edge marked by a professional doctor to compare the segmentation results. The method in [11] can not segment the target region and shows block effect. Furthermore, the segmentation method has no uniformity and homogeneity on segmentation results. The method in [12] segments the interested target but the target area is less than that marked by the doctor and the segmentation result contains much noise. Comparatively, the area of the segmented target by GIT-PCNN is very close to the marked area and contains little noise.

The presence of speckle, generated by the coherent processing of radar echoes and low resolution makes automatic segmentation of Synthetic Aperture Radar (SAR) images difficult. Therefore, a SAR image is segmented by the proposed GIT-PCNN to verify the effectiveness.

(a)

(b)

(c)

Figure 8 segmentation results (a) original SAR image (b) the method in [11] (c) the method in [12] (d) GIT-PCNN

(d)

Fig. 8 is the segmentation results of three algorithms. (a) is the original SAR image, including road and background. The segmentation target is to separate the foreground road from the background. (b), (c) and (d) are the segmentation results obtained by using methods in [11], [12] and the proposed GIT-PCNN, respectively. The result in (c) shows block effect, in which much details are segmented on the below middle block but the target can not be segmented from the background in some blocks, such as black block at the upper part. The results obtained by [11] and the GIT-PCNN have similar segmentation coherence and connectivity, which the two methods have similar segmentation performance in visual.

• B.    Subjective evaluation to segmentation performance

In order to subjectively evaluate the proposed segmentation method, regional consistency parameter U_r and regional contrast parameter C_r are used.

Ur =1-(σ12+σ22)/A(11)

where A is the number of image pixel.

σi2=∑ [I(x,y)-µi]2

( x , y ) ∈ R i

µi= ∑ I(x, y) /Bi(13)

(x,y)∈Ri whereI(x, y) is the grayscale level of pixel(x, y) and Bi is the number of pixels in region Ri .

Table 1 performance comparison of three segmentation algorithms

images	Method in [11]		Method in [12]		GIT-PCNN
	U r	C r	U r	C r	U r	C r
Lena	0.9940	0.4041	0.9938	0.3506	0.9944	0.4079
Cameraman	0.9718	0.4102	0.9935	0.2401	0.9753	0.7384
Coins	0.9995	0.4284	0.9997	0.4115	0.9997	0.4616
Blood	0.9994	0.3751	0.9233	0.2759	1.000	0.4820
inflammatory
ultrasound	0.9972	0.6687	0.9874	0.3126	0.9919	0.6220
lymphonodus
SAR	0.9858	0.3235	0.9796	0.1440	0.9880	0.3123

From table 2 it is obvious that the proposed GIT-PCNN is faster than the methods in [11] and [12] because the GIT-PCNN uses the grayscale iteration threshold and does not require iteration.

• IV.    Conclusions

In this paper, we use grayscale iteration threshold PCNN firing matrix, which includes not only the intensity but also the geometry structures of the image to segment image. The proposed method presents many advantages in comparison with traditional method for image segmentation.

• •    The threshold of traditional PCNN is improved to be the grayscale iteration threshold which is related to the grayscale statistics of the original image.

• •    The GIT-PCNN fires based on the proposed threshold so no iteration or specific rule, used as the iteration stop condition, is required. Therefore the GIT-PCNN is faster than other PCNN based segmentation algorithms.

• •    The experiment result demonstrates that the proposed method can achieve good segmentation results and the GIT-PCNN is evaluated objectively and subjectively.

The proposed method can be used to segment many types of images but it is still can not be effective to all types of images.

Acknowledgment

Table 1 demonstrates that the proposed GIT-PCNN has better performance than the results of methods in [11] and [12] except that the U_r and C_r of [11] are better than those obtained by the proposed GIT-PCNN when processing the inflammatory ultrasound lymphonodus image. After analyzing the two segmentation results it is because that the method in [11] segment the below part of the image but the proposed GIT-PCNN filters the below part as background. Even through the objective evaluation shows that the method in [11] is better than the GIT-PCNN but the segmented area of GIT-PCNN is most similar to the interest area marked by the doctor.

• C. Speed performance

Besides objective and subjective visual evaluate, speed is an important factor to evaluate the performance of an algorithm.

Table 2 the iteration time and processing time of three methods when segmenting image with size of 256*256 (unit: time and second)

Method in [11]		Method in [12]		GIT-PCNN
Iteration time	processing time	Iteration time	processing time	Iteration time	processing time
20	67.91	20	10.18	1	7.62

Table 2 is the iteration time and processing time (in the unit of second) of the three methods when processing an image with the size of 256*256. Each method was applied to segment the image 30 times and get the average processing time in order to make table 2 more subjective.

This work was supported by the Grant (2008YB009) from the Science and Engineering Fund of Yunnan University, the Grant (21132014) from the Young and Middle-aged Backbone Teacher’s Supporting Programs of Yunnan University and the Grant (21132014) from on-the-job training of PHD of Yunnan University.