A Novel Particle Swarm Optimization Algorithm Model with Centroid and its Application

Published Online October 2009 in MECS

• I.    I NTRODUCTION

  Particle Swarm Optimization (PSO) is one of the most powerful methods for solving complex optimization problems of the objective function having multi-peak and non-linear characteristics. It is a swarm intelligence computing technology proposed by Eberhart and Kennedy in 1995[1,2], inspired by based on the social behavior metaphor of bird flocking or fish schooling. Compared with other evolutionary methods, for its simple concept, easy implementation and quick convergence, nowadays PSO has gained much attention and has been successfully applied in many areas, including function optimization [3-5], fuzzy system control[6,7], artificial neural network training[8-10] and so on.

Because PSO has problems of easily falling into local solution, slow local convergence speed and low convergence accuracy, and often failed in searching the global optimal solution especially for nonlinear and multi-peak optimization problems. Since its first publication, on the basis of the standard PSO model, more and more research has been done to study the

Manuscript received January 21, 2009; revised June 18, 2009; accepted July 19, 2009.

performance of PSO and to improve its convergence performance by parameter selection and optimization [11-13], mutating of position and velocity of particle [14,15] or merging other optimal algorithms[16-19], and all these are on the basis of the standard PSO model. In this study, in order to improve search speed and success rate of convergence, on the basis of analysis of intelligent behaviors of social groups, a novel particle swarm optimization model (PSOM) is proposed by introducing centroid of particle swarm in standard PSO model to enhancing individual and group collaboration and information sharing capabilities. The results of the benchmark functions and application in material balancing computation show that new algorithms have faster convergence speed and higher globally convergence ability than PSO and improved PSO (AM-PSO[20],AF-PSO[21]) methods with both a better stability and a steady convergence.

• II.    PARTICLE SWARM OPTIMIZATION ALGORITHM

The particle swarm optimization algorithm is a stochastic optimization algorithm which maintains a swarm of candidate solutions, referred to as particles, they are members in the population, have their own positions and velocities, and they fly around the problem space in the swarms searching for the position of optima. PSO is initialized with a group of random particles and then searches for optima by updating generations. In every iteration, each particle is updated by following two "best" values. The first one is the best solution it has achieved so far. This value is called pbest . Another "best" value tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the population. This best value is a global best and called gbest . After finding the two best values, the particle updates its velocity and positions with following formulas.

vk1 = wxvd + cl Xrand(Mpd -xd)

+ c 2 ^xrand()^x(P gd ^- x kd )

k+1    кЛk xid = xid + vid( where d = 1, 2, . . .,N; i = 1, 2, . . . , M, and M is the size of the swarm; w is called inertia weight; c1, c2 are two positive constants, called cognitive and social parameter respectively; rand() are random numbers, uniformly distributed in (0, 1), and k = 1, 2, . . ., determines the iteration number ; pid is the position at which the particle has achieved its best fitness so far, and pgd is the position at which the best global fitness has been achieved so far; V*1 is the ith particle's new velocity at the k*h iteration; x *1 id                                                                                                                                                                                    id is the ith particle's next position, based on its previous position and new velocity at the kth iteration. The particles find the optimal solution by cooperation and competition among the particles.

• III.    A IMPROVED PARTICLE SWARM

OPTIMIZATION ALGORITHM MODEL AND ITS CONVERGENCE ANALYSIS

In traditional PSO model, each particle of the particles updates its next velocity and position only according to the velocity and position at the previous time, as well as individual best position and the best position of groups, during the searching process, because it lacks of collaboration and information sharing with other particles, most particles contact quickly a certain specific position. If it is a local optimum, then it is not easy for the particles escape from it. In such circumstances, in order to improve the speed and success rate of convergence, the centroid of particle swarm is introduced in the standard PSO model to improve global optimum efficiency and accuracy of algorithm through enhancing inter-particle collaboration and information sharing capabilities, then a new PSO model is proposed.

• A.    A Improved PSO Model (PSOM)

Let p_i be the best position of the i ^th particle then the centroid of particle swarm at the k ^th iteration can be defined as follow

M pk =—Ё р^             3)

M i=1

Let P d — x d be the distance of the particle’s current location and the centroid, so the formula (1) can be updated by

• V d ⁺¹ = w X V d * _{C 1} x rand () x ⁽ P d ^— x d ) *         ( 4 )

c 2 ^x rand ^{() x} ( p_g d — x d ) * c ₃ x rand () x ( p d — x kd ).

where c 3 is a positive constant similar to c 1 and c 2 .

Formula (4) and (2) are called as new particle swarm optimization model (PSOM). In this way, the running track of each particle is not only interrelated with individual best position and the best position of groups, but also with the centroid of the whole particle swarm, that is interrelated with individual best position of other particles too. So the collaboration and information sharing capabilities are enhanced greatly, the computing performance of algorithm is improved effectively.

During the searching process, as the iterations go on, each particle will converge to the local or global optimum. At same time, the optimal location of each particle, the globally optimal location of all particles, each particle's current position closes to the same position, and each particle's velocity closes quickly to 0. All the particles tend to equilibrium. In this case, according to the gathering degree and the steady degree of particle swarm[9], it can be determined whether partial or all the particles of current group will be mutated to escape from local solution and obtain the global optimum.

The new algorithm can be summarized as follows: Step1 Initialize position and velocity of all the particles randomly in the N dimension space.

Step2 Evaluate the fitness value of each particle, and update the global optimum position.

Step3 According to changing of the gathering degree and the steady degree of particle swarm, determine whether all the particles are re-initialized or not.

Step4 Determine the individual best fitness value. Compare the p_i of every individual with its current fitness value. If the current fitness value is better, assign the current fitness value to p_i .

Step5 Determine the current best fitness value in the entire population. If the current best fitness value is better than the p_g , assign the current best fitness value to p_g .

Step6 For each particle, update particle velocity according formula (4), Update particle position according formula (2).

Step7 Repeat Step 2 - 6 until a stop criterion is satisfied or a predefined number of iterations are completed.

• B.    The Convergence Analysis Of PSOM

To simplify the analysis, here the analysis is restricted to one dimension, and not consider random factors of the algorithm. Let Ф 1 = c 1 rand () , Ф 2 = c ₂ rand () , Ф 3 = c 3 rand () , then the formula (4) and (2) can be written as

• vk+1 = wvk * Ф1 x (P.— xk ) *

Ф 2 ^{x (} Pg ^— x ^k ) * Ф з ^{x (} P k ^— x ^k )

• „ k * 1       к . к * 1

• xi   = xi * vi(

Based on the above formula, we can obtain к*1

x =(1 * w—Ф1— Ф2— Ф3) x, — wxk—1 * Ф1P, * Ф2Pg * Ф3Pk let

	k 1 * w — Ф 1 — Ф 2 — Ф з   — w   Ф , P i * Ф 2 P g * Ф 3 P
G =	1                0             0
	0                0             1

Then formula (7) can be expressed into a matrix-style form ：

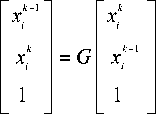
（9） where the characteristic polynomial of the coefficient matrix is

( Л - 1)(Л² - Л (1 + w -ф 1 -ф ₂ -ф ₃) + w ) = 0 ( 10 ) there are three characteristic roots, the three roots of characteristic equation are

^Л , = 1

■ Л 2	1 + w - ф 1		- ф 2	- ф 3 +Д	/ (1 + w - ф 1		- ф 2	2 - ф 3 )	- 4 w
					2
Л	1 + w -	ф 1	- ф 2	- ф 3 -\	/ (1 + w -	ф 1	- ф 2	2 - ф 3 )	- 4 w
					2

（ 11 ）

Therefore, the formula (7) can be written as xk = b1 + b2 Л2k + Ь3Л3k take the limit of k, have lim xk = lim(b1 + b2 Л2 k + b3 Л3k)

k ^^      k ^^

= b 1 + b ₂ lim Л ₂ ^k + b 3 lim Л 3 ^k k ^^         k ^^

（ 12 ）

（ 13 ）

where b1 , b2 and b3 are constants relating to to , ф1 , ф2 , ф3 , p , , pg and pk . Obviously, when

||Л 2 11 >  1 (when Л 2 is real, || Л 2|| is the absolute value, when Л 2 is plural, || Л 2|| indicates a value of its mode ) or || Л 311 >  1 , obviously the limit does not exist, the trajectories of particles is the divergence, when || Л ₂|| <  1 and || Л ₃| |< 1 , then the limit is existent , the particle’s trajectory is convergent, there are

	b 1 + b 1	ifl ^ 2 1-1-11 ^ 3 II <1
lim x =	b 1 + b 3	if ^ 2 K1-11 ^ 3 11=1    ....
k ^^	b 1 + b 2 + b 3	f ^ 2 II-1- 11 ^ 3 11= 1
	b 1	if| 2 , к1,1 Л , II <1

Then we can draw the following theorem.

Theorem the necessary and sufficient conditions in the convergence of PSOM algorithm is max (||Л2||,||Л3||) < 1.               (15)

Following, we study selection range of parameter in the convergence of PSOM algorithm. Let

A = (1 + w - ф 1 - ф ₂ - ф ₃)² - 4 w        ( 16 )

(1) If A >  0 , then Л ₂ , Л 3 are two real roots from max (I | Л 2|.|| Л 3|| ) <  1 , it can be seen

• - 2 <  1 + w - ф 1 - ф ₂ - ф ₃ + ^ (1 + w - ф 1 - ф ₂ - ф ₃ ) ² - 4 w <  2

• - 2 <  1 + w - ф 1 - ф ₂ - ф ₃ - (1 + w - ф 1 - ф ₂ - ф ₃ ) ² - 4 w <  2

( 18 ) from formula (17) and (18), we can obtain

• - 2 <  1 + w - ф 1 - ф ₂ - ф ₃ <  2            ( 19 )

At this point, it does not guarantee A >  0 , obviously, the system is instability. The trajectory is in a state of critical convergence or divergence.

• (2) When A <  0 , then Л ₂, Л 3 for the two complex roots,they are conjugated, its amplitude is

(1 + w - ф1 - ф2 - ф3 )2 + (1 + w - ф1 - ф2 - ф3 )2 - 4 w у/2(1 + w - ф1 - ф2 - ф3 )2 - 4 w

According to convergence conditions, above formula is not more than 1, there

2(1 + w- ф1 - ф2 - ф3)2 - 4w < 2

• (1 + w - ф1 - ф2 - ф3)2 - 2w < 2

• -V2 + 2w < (1 + w- ф1 - ф2 - ф3) < V2 + 2w(

1 + w - V 2 + 2 w <  ф 1 + ф ₂ + ф ₃ <  1 + w + V 2 + 2 w

Because, the values of ф 1 , ф ₂, ф ₃ , w are greater than 0 in the particle swarm algorithm, so there are

0 <  ф 1 + ф ₂ + ф ₃ <  1 + w + V 2 + 2 w       ( 25 )

Therefore, the values of correlation parameter can be determine according to above formula.

Corollary if the formula(25) is satisfied, then the PSOM algorithm is convergent.

Obviously, when c ₃ is 0, the PSOM algorithm is standard PSO.

• IV.    C OMPUTATION RESULTS AND ANALYSIS

To test the performance of the new algorithm models, firstly, two benchmark functions are introduced to test the new model, then, it is applied to the material balance computation of alumina production process, the final results of the new models are compared with standard PSO and other improved methods.

• A.    Benchmark function simulation

⑴ Rastrigin function

f ( x ) = ^ ( x" - 10cos(2 ^x ) + 10) ,     - 5.12 <  x <  5.12       (26)

l =1

• (2)    Rosenbrock function

n

f ( x ) = ^ [100( x , +1 - x , ²) ² + ( x - 1) ² ] , -30< x <30 , (2!j^)

i =1

(3$) Schaffer function sin 2л/х2 + x22 -0.5

f ( x , x ) = 0.5 +----------------------,    - 100 <  x <  100 (28)

• ¹    2            1 + 0.001 - ( x ,² + x ₂ ² )                 '

PSO, AM-PSO, AF-PSO, PSOM are respectively run for 50 times, the swarm sizes are 60, c 1 =c 2 = 2.0 for PSO, AM-PSO and AF-PSO, c 1 =c 2 =c 3 = 1.4 , w is declined linearly from 0.9 to 0.4. Other parameters are set in Table 1. Comparisons of PSO, AM-PSO, AF-PSO , PSOM are shown in TABLE 2, Figure 1-2.

TABLE 1. CONGURATION OF SOME PARAMETERS

Function	Dimension	Generation	Precision
Rastrigrin	30	2000	50
Rosenbrock	30	2000	100
Schaffer	2	1000	1e-5

TABLE 2. COMPARISON OF THE COMPUTATIONAL RESULTS

Function	Algor -ithm	Fitness value				Succ -Rate (%)
		Best	Worst	Mean	Deviation
Rast-rigin	PSO	0	115.69	33.753	922.36	76
	AF-PSO	0	82.770	17.849	414.31	94
	AM-PSO	0	54.464	16.462	170.98	98
	PSOM	0	46.901	15.971	164.69	100
Rosen-brock	PSO	232.3	3696.8	872.96	423616	0
	AF-PSO	35.59	142.37	79.089	485.07	86
	AM-PSO	40.07	153.44	75.762	368.62	90
	PSOM	12.86	53.69	32.339	102.80	100
Schaffer	PSO	0	9.72e-3	1.16e-3	1.02e-5	88
	AF-PSO	0	1.31e-2	2.62e-4	3.43e-6	98
	AM-PSO	0	0	0	0	100
	PSOM	0	0	0	0	100

PSO AF-PSO AM-PSO PSOM

V)

250 о

50 0

0    200   400   600   800  1000 1200 1400 1600 1800 2000

Iteration

Figure 1. Comparisons of convergence curve for Rastrigin function

From Table 2, it can be seen that there are higher convergence rate and accuracy for the PSOM than that for the PSO, AF-PSO and AM-PSO, from the mean and deviation in Table 2, the PSOM is better than the PSO, AF-PSO and AM-PSO, with both a better stability and a steady convergence, and the average success rate of PSOM for each test functions reaches 100%, and obviously better than those of PSO, AF-PSO and AM-PSO. From Figure 1-3, it can be seen that there are higher convergence speed and accuracy for the PSOM than for the PSO, the PSOM can easily escape from local optimum solution through individual and group collaboration and information sharing, and attain global optimum solution while the PSO cannot. All these results demonstrate that the PSOM is more feasible and efficient than the PSO, AF-PSO and AM-PSO.

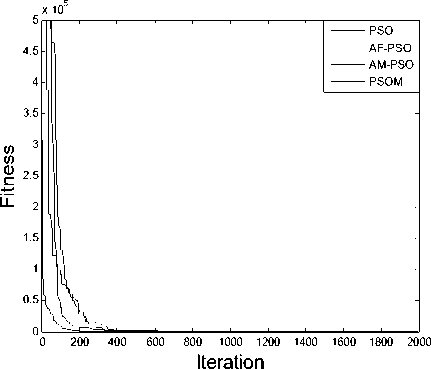
Figure 2. Comparisons of convergence curve for Rosenbrock function

PSO AF-PSO AM-PSO PSOM

0.16

0.14

0.12

0.1

w V)

0.08

0.06

0.04

0.02

0        100       200       300       400       500       600

Iteration

Figure 3. Comparisons of convergence curve for Schaffer function

• B.    The material balance computation (MBC) in alumina production process

Material balance is the core of alumina production, the material balance calculation for alumina production is very important; it is an important method for guiding the production and the technical design. Although there are many technical projects to construct a new alumina plant, only through the material balance computation, can we select the best technical process and production method, and attain the purpose of the lowest cost and the lowest investment. The production process of alumina is very complicated, it can be seen as a complex control system[22,23], as a result, it causes calculating complexity of its material balance with tedious. Many processes of which come down to the revert computation, each of these processes has a direct impact on the results of material balance calculation of the entire process, which results in calculating complexity of its material balance with tediousness.

Based on the analysis and the actual deduction of the entire process, which does not include the storage and transportation of limestone, lime burning process, and the composition of lime is known , it must satisfy seven equation and two balance relation formula: © the conservation of additive soda quantity, © the conservation of alumina, © the conservation of alumina of cycle mother liquor, ф the conservation of caustic alkali of cycle mother liquor, © the conservation of alumina of red mud washing, @ the conservation of caustic alkali of red mud washing, © the conservation of carbon alkali of red mud washing, © the balance relation between finished alumina hydroxide and aluminum in the roasting process, © The control relation of water quality in the entire flow.

The balance equations © - © are objective functions bound to meet two constraint conditions © and © . The material balance calculation on the whole can be turned into solving a nonlinear multi-objective constrained optimization problem:

min G ( X ) = min( g, ( X ), g ( X ), L , g , ( X )) T

_{8 8} 1 2 7

X e R X e R

R = { X I g c ( X ) < 0}, g c ( X ) = ( g 8 ( X ), g 9 ( X )) T ( 29 )

X = ( X 1 ,X ₂ ,L , X 8 ) T , X e R c E ⁸

where G ( ^X ) is optimization, ^g c (^X) is constraint vector, X is variable vector, ^x _i (i ⁼ 1 ^, K ^, 8) is respectively the quality of alumina in finished aluminum products, the quality of alumina in finished aluminum hydroxide products, the quality of additive soda in recombined process of mother liquid, the quality of alumina in red mud lotion, the quality of caustic alkali in finished red mud lotion, the quality of carbon alkali in red mud lotion, the total quality of red mud lotion and the quality of water in the evaporation process.

This is a typical solving nonlinear and multi-objective optimization problem. PSO, AM-PSO, AF-PSO and PSOM are respectively run for 50 times. The population sizes are 100, and the maximum evolution generation is 2000, other parameters are set as follows: c 1 =c 2 =2.0 for PSO, AM-PSO and AF-PSO, c 1 =c 2 =c 3 =1.4 for PSOM, w is declined linearly from 0.9 to 0.4, the ranges of X ’s value in multi-objective optimization problem is set in TABLE 3. Comparisons of PSO, AM-PSO, AF-PSO and PSOM are shown in TABLE 4, Figure 4-11.

TABLE 4. COMPARISON OF COMPUTATION RESULTS OF PSO, AM-PSO, AF-PSO AND PSOM

Function	Algor -ithm	Fitness value				Succ-Rate (%)
		best	worst	mean	deviation
Multiobjective optimization Problem ( 29 )	PSO	0.1795 6576	6.859 9641	0.592 93555	1.110789	72
	AF- PSO	0.1795 6574	1.698 1267	0.375 32116	0.1355591	80
	AM- PSO	0.1795 6576	1.032 2167	0.227 59169	1.987e-3	96
	PCOM	0.1796 1679	0.550 8336	0.233 8919	7.6691e-3	98

V)

p

E

E

c

£

О

U Ф

V)

20           30

Runs

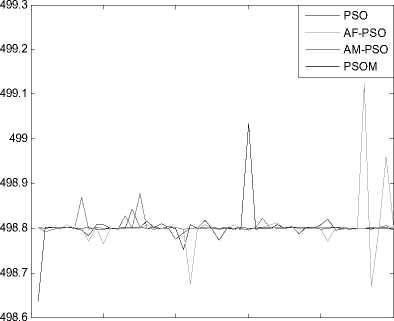
Figure 4. The quality of alumina in the finished aluminum products for 50 times iteration

Runs

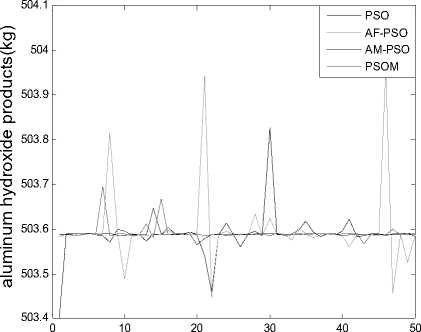
Figure 5. The quality of alumina in the finished aluminum hydroxide products for 50 times iteration

TABLE 3. THE RANGE OF X ’S INITIAL VALUE

Variable	x 1 , x 2	x 3 , x 4 , x 5	x 6	x 7	x 8
Initial range	[200,600]	[5,300]	[5,200]	[5,5000]	[100,500]

108.5

107.5

Ф

106.5

о

V) (Л

о

(Л

ф

PSO

AF-PSO

AM-PSO о Е

Е

О

Runs

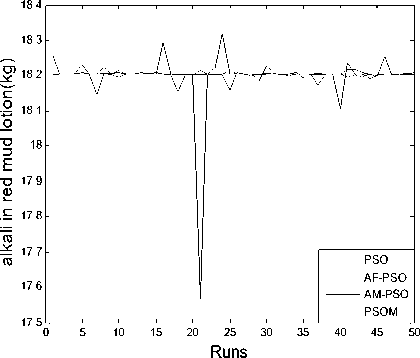
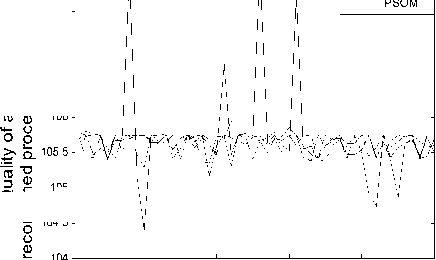
Figure 9. The quality of carbon alkali in the red mud lotion for 50 times iteration

Figure 6. The quality of additive soda in the recombined process of mother liquid for 50 times iteration

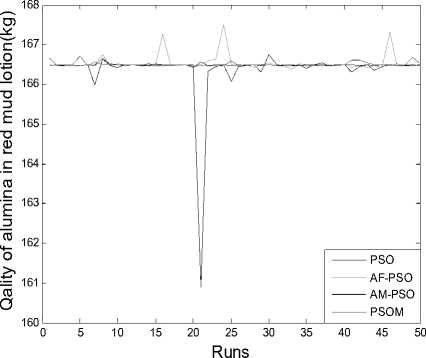
Figure 7. The quality of alumina in the red mud lotion for 50 times iteration

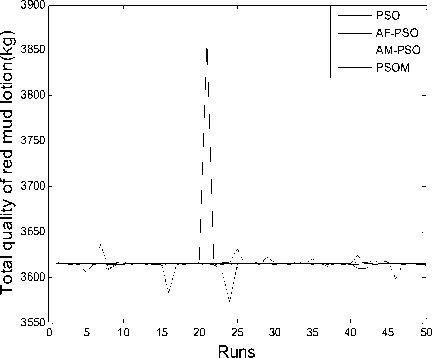
Figure 10. The total quality of red mud lotion for 50 times iteration

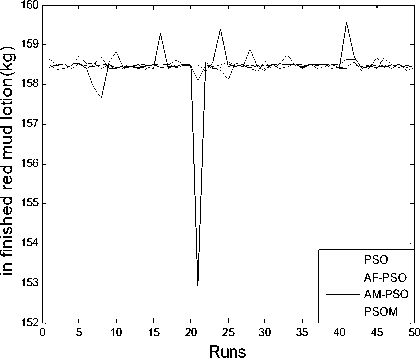
Figure 8. The quality of caustic alkali in the finished red mud lotion for 50 times iteration

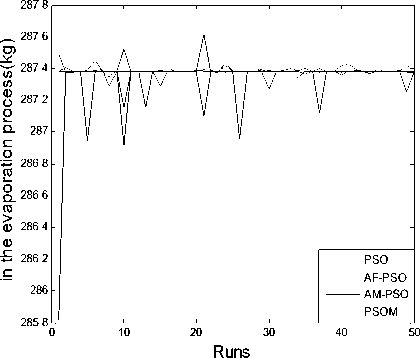
Figure 11. The quality of water in the evaporation process for 50 times iteration

From TABLE 4, we can see that there are higher convergence success rate and accuracy for the PSOM than for the PSO, AF-PSO and AM-PSO, the PSOM can especially avoid falling into local optimum solution with through cooperation and information sharing with other particles and attain global optimum solution while the PSO cannot. From mean and deviation in TABLE 4 and Figure 4~11, the PSOM has a better stability and a steady convergence, the average success rate of new algorithm is better than those of PSO, AF-PSO and AM-PSO. All these results demonstrate the PSOM is more feasible and efficient than the PSO and AM-PSO.

• V.    CONCLUSION

The standard PSO algorithm is easy to fall into local optimum solution, and in order to solve this problem effectively and to improve the convergence performance of the PSO, an improved particle swarm optimization model with the centroid of particle swarm is proposed , which can enhance individual and group collaboration and information sharing capabilities effectively. The exploration ability is greatly improved by the centroid, and the probability of falling into local optimum is efficiently decreased. Experimental and application results show the PSOM has faster convergence speed and higher globally convergence ability than the traditional PSO. In the view of the authors, the application of the PSOM in other areas can be discussed further in future and the convergence pattern, dynamic and steady-state performances of the algorithm can be improved more to specific complex optimization functions through combining with other evolutionary computation technique.

A CKNOWLEDGMENT

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the National High Technology Research and Development Program of China under grant no. 2006AA060101.