A Novel Reduced-Precision Fault-Tolerant Floating-Point Multiplier

Published Online June 2017 in MECS

Arithmetic operations are one of the primary functions of computer systems. This type of operations is required for many embedded systems, especially the ones used in multimedia applications [1, 2]. In particular, many categories of software perform vast amounts of floatingpoint arithmetic operations. Meanwhile, the floating-point multiplication unit is an essential intellectual property (IP) component for modern multimedia and high performance computing such as graphics acceleration, signal processing, image processing, etc. A lot of effort is made over the past few decades to improve the performance and reliability of floating-point computations since the floating-point multipliers require more area and power consumption compared to their fixed-point counterparts.

Because floating-point arithmetic operations are crucial for many applications, there are many situations in which an error in a floating-point calculation could be problematic or even disastrous. Moreover, decreasing feature sizes has led to reliability problems [3, 4]. Errors can arise due to physical faults caused by the strike of high-energy particles or permanent wear out of transistors because of continuation of shrinking the transistor and wire dimensions.

The reliability and low power consumption are two major design objectives in today’s embedded systems. Since Floating Point Units (FPUs) are required for many embedded applications, a careful consideration should be given to the reliability and power consumption of FPUs used in the embedded systems.

Many floating-point applications in multimedia and scientific computing do not require the complete precision, and even an approximate value will be sufficient for the correct operation [5]. Such floatingpoint applications can tolerate imprecise computations. In fact, many floating-point applications can operate with reduced-precision floating-point values, so we can remove some Least Significant Bits (LSB) of mantissa in the floating-point values that are used in the computations. As a result, a part of the circuit is released that can result in a lower power consumption. However, in this paper, we add and utilize some new parts for providing redundant computations in order to enhance the reliability in the form of error detection and error correction. This way, we focus on error detection and error correction in the floating-point multiplier architecture and present two new 32-bit fault-tolerant floating-point multiplier designs, one with error detection and another with error correction capability. However, the main goal is to achieve the new fault-tolerant designs with the hardware cost very close to the original design.

The proposed designs are compatible with the singleprecision representation format of floating-point values based on IEEE-754 standard. It is worth mentioning that as the proposed designs are based on reduced-precision computations, some computational errors may be produced in the outputs. Therefore, we achieve to a reliable floating-point multiplier against a variety of permanent and transient faults by accepting a few percent computational error in the outputs which is satisfactory in many multimedia applications because some output deviations are naturally hidden due to the limitation of human sense.

The rest of the paper is organized as follows: In Section II the related works, and in Section III, the backgrounds for IEEE floating-point standard and singleprecision floating-point multiplier are presented. Section IV describes the proposed fault-tolerant multiplier designs. Section V shows the experimental results and evaluates the proposed designs in terms of delay, power consumption and area. Finally, some conclusions are drawn in Section VI.

• II.    Related Works

FPUs, in particular their floating-point multipliers, are among the most crucial and hardest components to protect. So the fault-tolerance capability of such units against faults is one of the important issues which require much attention. There are several techniques to improve reliability. However, these techniques impose a sort of overheads including power consumption, delay overhead and area overhead. Traditional fault or error detection/correction techniques, such as duplication with comparison, Triple Modular Redundancy (TMR), and the methods based on time redundancy (re-execution) [6] are used in some of the practical floating-point processors. However, these techniques suffer from high area and power overheads.

So far, many fault-tolerant fixed-point arithmetic operators or units have been designed such as [7-12]. However, the fault-tolerant floating-point arithmetic units have received less attention. In [13] a floating-point arithmetic unit with error detection capability is proposed in which a cost-efficient and complete residue checking is utilized. However, because of the utilized original method, it cannot be used for error correction. In [14] an exponent checking architecture is proposed for floating-point computations, which detects many errors but apparently it can detect fewer errors compared to the augmented design in which the mantissa is checked for errors. Similar to [13], this design is only useful for error detection.

Previous reduced-precision or bit truncation schemes [15-18] focused on reducing the power consumption in the mantissa multiplication block, due to the fact that it consumes the largest amount of power consumption in a floating-point multiplier. In [15], it is examined that how a software-based system can employ the minimal number of bits for mantissa and exponent in the floating-point hardware to reduce the power consumption while maintaining the program’s overall accuracy. This study shows the relationship between the accuracy of floatingpoint programs and the number of bits used in the representation of their data. The experimental results stated in [15] show that none of the floating-point programs displays a noticeable degradation in accuracy when the bit width of mantissa is reduced from 23 to 11. Moreover, for some programs, the accuracy does not change significantly with as few as 5-bit mantissa. The results demonstrate that many programs which manipulate human sensory inputs, e.g. speech and image recognition, suffer no loss of accuracy with reduced bit width in the mantissa or exponent. However, limited studies have been performed based on reduced-precision to achieve error detection capability for floating-point adders and multipliers. Moreover, there is not any research regarding error correction in the reduced-precision FPUs.

In [19] an error detection technique for a floating-point adder is presented which uses a reduced-precision checker adder to determine whether the result is correct within some error bound. In this technique, the same amount of bits for the exponent is maintained due to the fact that the exponent highly influences the last result and thus should not be truncated, but the mantissa is truncated to save area and power. The full computation is done in parallel with the redundant computation, with the reduced-precision checker adder which performs the redundant computation, only taking the Most Significant Bits (MSBs) of the operands. In the last stage of the design there is a hardware that compares the results and determines whether there is an error or not. In [20] the Reduced Precision Checking (RPC) technique has been applied to the floating-point multiplier to detect errors. This study shows that the RPC can successfully detect errors in floating-point multiplication at relatively low cost but cannot correct errors.

• III.    Background

• A.    IEEE Floating-Point Representation

The most common representations used for real numbers are in the form of fixed-point or floating-point. The floating-point representation provides both a wider dynamic range and a higher precision as compared to the fixed-point representation, but it incurs a higher area and power consumption, as well. The usual display of floating-point numbers is determined according to IEEE-754 standard. In this standard two main representation formats are defined. The first format called singleprecision format is 32 bits wide, containing one bit for the sign, 8 bits for the exponent and 23 bits for the mantissa. The second format called double-precision format is 64 bits wide, containing one bit for the sign, 11 bits for the exponent and 52 bits for the mantissa. In this paper, we focus only on the single-precision format. However, the proposed architecture can be extended to doubleprecision numbers. Fig. 1 demonstrates the binary representation of the single-precision floating-point format.

According to the IEEE-754 standard, the mantissa is less than 1.0, but one hidden bit, which is always '1', is supposed to be placed on the left of the implicit binary point and forms the significand. Therefore, the significand is a normalized number in the range of [1, 2). In this representation, the exponent is modified with a bias of 127 (that is equal to 2number of exponent's bits-1-1) for the

- 1 Sign X l.Mantissa x 2 Exponent ^{- 12}7

Sign (1-bit)

Biased Exponent (8-bit)

Mantissa (23 bit)

Fig.1. Binary representation of single-precision format.

single-precision format for some reasons that one of them is the representation of zero number with only zero bits. In addition, the sign bit represents the sign of significand while the sign of exponent is implicit inside it due to the fact that the two's complement representation is used for the exponent. The floating-point values based on different amounts of exponent and mantissa, are depicted in Table 1.

• B.    Single-Precision Floating-Point Multiplier

The single-precision floating-point multiplier performs the multiplication of two 32-bit inputs which are floatingpoint numbers with single-precision format and provides the output in the same format. The multiplication of two floating-point numbers is performed in six steps as the following:

• •    Step 1: Multiplication of significands

• •    Step 2: Normalization

• •    Step 3: Adding the exponents

• •    Step 4:   Checking for underflow/overflow

occurrence

• •    Step 5: Calculating the sign

• •    Step 6: Standardizing

Fig. 2 depicts the 32-bit floating point multiplier's data process flow. Each input is split into three parts (sign, exponent, and mantissa) so that can be easily routed into the corresponding components. The signs from the input operands A and B are connected directly to an XOR gate to generate the sign of the final result, in which '0' indicates the positive sign and '1' indicates the negative sign. The 23-bit mantissas are extracted from two operands to be sent to the multiplication unit. However, an explicit '1' is appended as the leading bit of both mantissas to produce the significand and fit into the 24-bit multiplier unit. The output of the 24-bit multiplier is a 48-bit result, but only 23 bits are extracted in order to follow the IEEE-754 standard rules. Thus, the 48-bit output of the multiplier should pass through the normalizer to be rounded to nearest 23-bit result of mantissa. The extraction of 23 bits out of 48 bits in the output after multiplication, as the final result for mantissa, has two conditions. It may also involve an adjustment of the resultant exponent, depending on the MSB of the 48-bit multiplication's output. If this bit is equal to '1', one carry bit is given to the exponent calculation block to set the final exponent.

Condition1: If the MSB (48th bit) is equal to '1', the bits with the indices from 25 to 47 will be selected as the final 23-bit mantissa with rounding to nearest by adding 24th bit, and adding '1' to the exponent (carry is one).

Table 1. Floating-Point Values Based on Different Amounts of Exponent and Mantissa

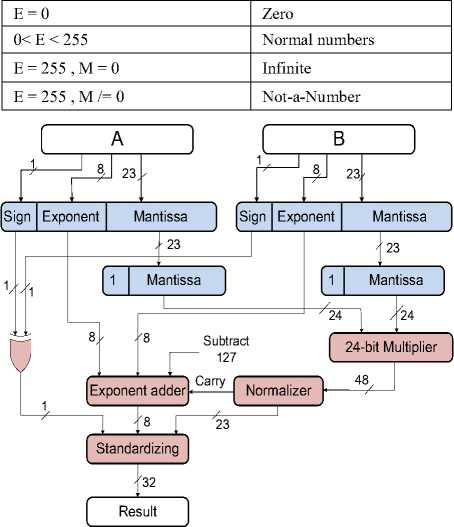
Fig.2. The baseline 32-bit floating-point multiplier.

Condition2: If the MSB (48th bit) is equal to '0', then the bits with the indices from 24 to 46 will be selected with rounding to nearest by adding 23th bit without adding a carry to the exponent (carry is zero).

The 8-bit exponent values from two operands are added to generate a sum of 9-bit result. The incoming values are biased, so a constant value of 127 must be subtracted from the result. In addition, the carry signal from the normalizer is added to this exponent for adjustment. Only the 8-bit exponent values are forwarded to the final output, which will be the 8-bit exponent in the IEEE-754 32-bit floating-point number. Equation (1) is used to obtain the sum of exponents:

Exp. (Sum) = Exp. (A) + Exp. (B) –

127 + Carry from Normalizer (1)

Moreover, the MSB (9th bit) is used to show that either overflow or underflow has occurred in the exponent. If the MSB of the exponent is equal to '1', it means the exponent value is overflowed (infinite value), and if it is '0', it means the exponent is under flowed (nearly zero value).

Finally, the 32-bit output passes through the standardizing block. This block, as its name shows, is responsible for displaying the multiplication result according to the IEEE-754 standard. In addition, there are some special cases in which the mentioned steps are not needed and the answer can directly be obtained. Some of these special cases are shown in Table 2.

Table 2. Some Special Cases for Floating-Point Multiplication

Operand A	Operand B	Output
Normal	Zero	Zero
Normal	Infinite	Infinite
Normal	Not-a-Number	Not-a-Number
Infinite	Infinite	Not-a-Number
Infinite	Not-a-Number	Not-a-Number

In the following sections, two new architectures based on single-precision floating-point multiplier are proposed and evaluated for error detection and error correction in such a way that the overall required hardware becomes almost the same as the primary multiplier.

• IV.    Proposed Designs

Many floating-point applications in multimedia and scientific computing can tolerate imprecise computations [5, 15]. In fact, many floating-point applications can operate with single-precision format and even less precision with some truncated bits. However, output deviations in the form of errors are not acceptable. Thus, the fault-tolerant methods should be considered in the floating-point operations to achieve error detection or error correction in the outputs. As the state of the art fault-tolerant methods incur noticeable area and power overheads, we utilize the bit truncation of mantissa in the proposed designs to reduce the overall consumed area while some types of redundancies are applied to achieve reliability in the form of error detection or error correction in the intended multiplier architecture. In other words, the precision reduction resulted by the bit truncation of mantissa in the floating-point representation of the input operands causes some blocks of the baseline multiplier to be smaller and thus require less area and power. This helps us to incorporate some redundancies to achieve a fault-tolerant multiplier. In this way, regarding the size of mantissa, the new designs can be attained with almost the same hardware cost as the primary design which is one of the main goals of this paper.

• A.    Floating-Point Multiplier with Error Detection

As mentioned in Section III, the single-precision format according to the IEEE-754 standard has a bit for the sign, eight bits for the exponent and 23 bits for the mantissa, and there is also a hidden bit '1' on the left of the mantissa which forms the significand. To achieve an error detecting floating-point multiplier design, we maintain the same number of bits for the exponent since it highly influences the magnitude and the range of displayable floating-point numbers. However, the truncation of some LSBs of the mantissa is performed to compromise precision and reliability.

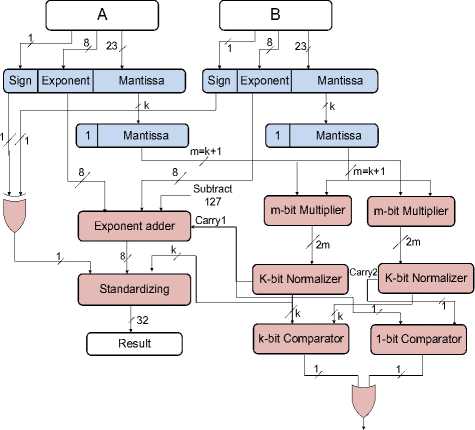
As shown in Fig. 2, the 32-bit floating-point multiplier described before includes an internal 24-bit multiplier for multiplying two 24-bit significands of the input floatingpoint operands. Thus, to achieve error detection capability in the multiplier, the largest part of the architecture, two m-bit reduced-precision internal multipliers (m<24) are utilized according to the concept of duplication with comparison method. Therefore, each 23-bit mantissa is truncated to a new k-bit mantissa (which means (23–k) LSBs are removed) which together with the hidden bit forms an m-bit significand (m=k+1). This way, instead of using a large 24-bit internal multiplier with a 48-bit result, two m-bit reduced-precision multipliers are utilized to produce two 2m-bit results to be compared in the comparator in order to detect probable errors with minimum hardware overheads.

Fig. 3 depicts the proposed reduced-precision fault-tolerant floating-point multiplier with error detection capability. As shown in this figure, the normalizer block is also duplicated to reach more error detection capability in entire design. In addition, an error signal will be asserted if the results of two m -bit internal multipliers are not equal after passing the normalizer blocks or two produced carry signals from the normalizer blocks are not equal. The comparators will set their output to one if their input operands are not equal. Otherwise, one of the produced results will be sent to the remaining blocks (exponent adder and standardizing blocks) to produce the last result in the form of the 32-bit single-precision floating-point number. It should be noted that in the standardizing block, (23 – k ) zeros are appended at the right of the k -bit resultant mantissa to obtain the 32-bit standard result. As will be shown in Section V, a proper k value can be selected regarding the total hardware cost (area, power, delay) to obtain low-cost error detecting design with almost the same hardware cost as the primary design while reducing the output's precision.

• B.    Floating-Point Multiplier with Error Correction

It is clear that more cost is imposed if an error correcting multiplier is to be reached. Thus, to maintain the entire cost almost unchanged, more precision reduction is needed. This way, tree n -bit reduced-precision multipliers ( n < m <24) are utilized according to the concept of TMR method to correct single errors in the fault-tolerant floating-point multiplier. Therefore, each 23-bit mantissa is truncated to a new t -bit mantissa (which means (23 – t ) LSBs are removed) which together with the hidden bit forms an n -bit significand ( n = t +1). This way, instead of a large 24-bit internal multiplier with a 48-bit result, tree n -bit reduced-precision internal multipliers are utilized to produce tree 2 n -bit results to be compared in the voter in order to mask or correct probable errors.

Fig. 4 depicts the proposed reduced-precision fault-tolerant floating-point multiplier with error correction capability. In this figure, the normalizer block is triplicated similar to the internal multiplier to reach more error correction capability in entire design. In addition, two voters are utilized including a t-bit voter for masking single errors in the resultant mantissa and a one-bit voter for the output carries of the normalizer blocks. Then, the voters' outputs will be sent to the remaining blocks to produce the last result in the form of the 32-bit single- precision floating-point number. Similar to the error detecting multiplier, several zeros (23–t) are appended at the right of the t-bit resultant mantissa in the standardizing block to obtain the 32-bit standard result. As will be shown later, a proper t value can be selected regarding the total hardware cost to obtain a low-cost error correcting design while reducing the output's precision.

Error

Fig.3. Proposed 32-bit reduced-precision floating-point multiplier with error detection.

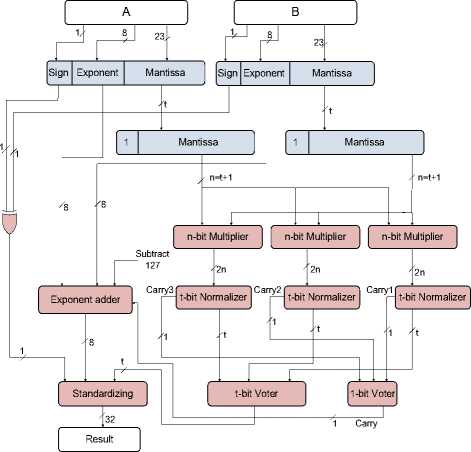
Fig.4. Proposed 32-bit reduced-precision floating-point multiplier with error correction.

• V.    Experimental Results

To obtain a proper size for fault-tolerant floating-point multipliers in which the required area and power become very close to the baseline multiplier, different precisions are investigated for the mantissa in two proposed architectures. Therefore, the baseline and the proposed designs are implemented with VHDL, and then, synthesized using Synopsys Design Compiler to obtain the area, power, and delay requirements of the baseline and the proposed designs while changing the bit width of mantissa i.e. k and t values in error detecting and error correcting architectures, respectively. The synthesis results shown in Tables 3 and 4 are according to CMOS 65 nm LPLVT STMicroelectronics standard cell library (with 1.2 V power supply in 25°C temperature).

Table 3 shows the required area, power and delay of the proposed error detecting floating-point multiplier with different precisions (15, 16, and 17 bits for mantissa) in addition to the baseline multiplier in which a 23-bit mantissa is utilized. This table also presents different overheads (O.H.) compared to the baseline multiplier regarding some parameters. Each negative overhead shows that the new multiplier with an specific size of mantissa ( k ) not only does not have any overhead in that parameter, but even outperforms compared to the basic non-fault-tolerant design. According to Table 3, an error detecting floating-point multiplier with k equal to 17 which means it includes two 18-bit internal multipliers instead of one 24-bit internal multiplier, requires a few percent area and power overheads compared to the baseline multiplier while its speed is still higher because it requires lower delay. In other words, the design with the 17-bit mantissa requires the area and power very close to that of the baseline multiplier. Therefore, it can be used instead of the baseline non-fault-tolerant floating-point multiplier.

It is worth mentioning that according to [15], using the 11-bit mantissa in representing the floating-point numbers is enough for many applications to produce the satisfying results. Thus, all the designs with 15-, 16-, or 17-bit mantissa shown in Table 3 can be used instead of the baseline floating-point multiplier. Especially, the designs with 15-bit or 16-bit mantissa require lower area, power consumption and delay compared to the baseline multiplier.

It should be noted that in the baseline floating-point multiplier, the main 24-bit multiplier solely consumes 85% of total area. Thus, making only this block fault-tolerant, will result in a high fault-tolerance capability in overall architecture. The last column of Table 3 shows error detection probability in the designs with different mantissa. This probability is simply obtained according to the area that each part of the design is consumed. Therefore, error detection probability shown in Table 3 is the area ratio of the parts with error detection capability in the proposed floating-point multiplier for different k values. This area ratio which corresponds to the error detection probability is obtained based on the fact that only duplicated parts and comparators in the new multiplier have error detection capability. Thus, for example, for k equal to 17, two multipliers, two normalizers, and the comparators including the last OR gate, consume 10118.2 um2, 376.5 um2, and 96.2 um2, respectively, which leads to the error detection probability equal to 89.4% respecting the total area equal to 11850.8 um2 in this design. It is clear that more error detection probability will be reached if a longer mantissa is used in the proposed design.

Table 4 shows the required area, power and delay of the proposed error correcting floating-point multiplier with different precisions (11, 13, 14 and 15 bits for mantissa) in addition to the baseline multiplier in which a 23-bit mantissa is utilized. This table also demonstrates different overheads compared to the baseline multiplier regarding the mentioned parameters. According to Table 4, an error correcting floating-point multiplier with t equal to 14 which means it includes three 15-bit multipliers instead of one 24-bit internal multiplier, requires the area and power consumption very close to that of the baseline multiplier. In other words, the design with the 14-bit mantissa requires only 5% area overhead compared to the baseline multiplier. In addition, it requires 3.6% less power and 20.3% less delay compared to the baseline multiplier. Thus, it can be used instead of the baseline non-fault-tolerant floating-point multiplier as a design with error correction capability while it requires less power and delay, as well. In addition, as the 11-bit mantissa is enough for many applications to produce the desirable results [15], all the reduced-precision designs shown in Table 4 can be used instead of the baseline floating-point multiplier.

Table 3. Proposed Error Detection Multiplier with Different Precisions Compared to the Baseline Multiplier

Size of mantissa in bits	Delay (ns)	Delay O.H.	Area (um2)	Area O.H.	Power (mw)	Power O.H.	Error Detection prob.
k=23 (Baseline)	8.70	NA	11290.2	NA	5.62	NA	NA
k=15	6.76	-22.3%	10098.4	-10.6%	4.39	-22.9%	89.2%
k=16	7.24	-16.8%	11213.8	-0.7%	5.08	-9.6%	89.1%
k=17	7.00	-19.5%	11850.8	+5.0%	5.77	+2.7%	89.4%

Table 4. Proposed Error Correction Multiplier with Different Precisions Compared to the Baseline Multiplier

Size of mantissa in bits	Delay (ns)	Delay O.H.	Area (um2)	Area O.H.	Power (mw)	Power O.H.	Error Correction prob.
t=23 (Baseline)	8.70	NA	11290.2	NA	5.62	NA	NA
t=11	5.69	-34.6%	7098.5	-37.1%	3.45	-38.6%	87.1%
t=13	6.42	-26.2%	10531.0	-6.7%	4.65	-17.3%	89.5%
t=14	6.93	-20.3%	11850.3	+5.0%	5.42	-3.6%	90.4%
t=15	6.81	-21.7%	14548.0	+28.9%	6.33	+12.6%	92.0%

Furthermore, similar to Table 3, the last column of Table 4 depicts the fault-tolerance capability in the form of error correction as a function of the size of mantissa. According to Fig. 4, the blocks in which all single errors will be masked or corrected include three n -bit multipliers and three t -bit normalizers. These blocks, for example for the design with t equal to 14, consume 10712.5 um² altogether which finally leads to 90.4% error correction probability respecting the total area that is equal to 11850.3 um². According to Table 4, it is apparent that more error correction probability will be reached if a longer mantissa is used in the proposed design. However, more hardware overheads will be required, as well.

As mentioned in Section II, the RPC technique [20] can be used for detecting errors in the floating-point multiplier. This technique in which the 32-bit floatingpoint multiplier is checked by a k-bit (k<23) reduced-precision floating-point checker multiplier, requires the area and power overheads equal to 17.8% and 35%, respectively, for the checker multiplier in which the mantissa with the size of only 7 bits has been used. It is clear that the area and power overheads for that method would be more for longer mantissa used in the checker. However, as shown in table 3, the required area and power overheads in our error detecting scheme are much lower, even with a longer mantissa. For example, the design with a 17-bit mantissa requires only 5% and 2.7% area and power overheads, respectively, while its precision is much higher than that of the checker in [20]. In addition, based on [15] the 11-bit mantissa is enough for many applications that verifies our proposed fault-tolerant designs.

Since the proposed fault-tolerant floating-point multipliers in this paper are based on output's precision reduction method, therefore, some small and limited computational errors will be produced at the output. However, in many applications especially the applications that are relevant to human senses such as hearing and vision, the precise computation is not required and some percent of computational errors is acceptable in the outputs. In other words, many floatingpoint applications in multimedia and scientific computing can tolerate imprecise computations. The estimation of maximum relative error is straightforward for a floatingpoint output, and can be calculated according to the following equation:

Maximum Relative Error = 2 ^-l (2)

In the equation above, l is the bit width of the mantissa used in the representation of floating-point number. Table

5 demonstrates the maximum relative errors in different multipliers with different precisions or bit width of mantissa. For example, in both proposed error detecting and error correcting multipliers in which m equal to 16 is used, the bit width of the mantissa (k) equals 15 which results in the maximum relative error equal to 2-15 or 3.05×10-5.

Table 5. Maximum Relative Errors for Different Multipliers with Different Precisions

Type of Multiplier	Error Cor.	Error Cor.	Both Error Cor. and Error Det.	Error Det.	Error Det.	Baseline
Size of mantissa in bits	13	14	15	16	17	23
Maximum Relative Error	1.22×10-4	6.1×10-5	3.05×10-5	1.53×10-5	7.63×10-6	1.19×10-7

• VI.    Conclusion

In this paper, two floating-point multiplier architectures were proposed beneficial for fault-tolerant computations especially for the applications that can tolerate imprecise computations. The first multiplier has error detection capability and the other has error correction capability. However, for both proposed multipliers, the width of mantissa can be selected so that they require almost the same hardware cost compared to the non-fault-tolerant baseline multiplier. This property is achieved by an appropriate output's precision reduction. In addition, the proposed multipliers have more speed compared to the baseline multiplier. In this technique, less precise multiplication is used which results in less hardware cost. Thus, more smaller and redundant multipliers can be utilized for error detection or error correction in the overall multiplication. The proposed multipliers can tolerate both the permanent and transient faults by accepting some percentage of errors in the output. The implementation results show that a proper fault-tolerant floating-point multiplier can be selected with almost the same area and power requirements compared to the baseline architecture while having an acceptable output precision for many floating-point applications.