A parallel evolutionary search for shortest vector problem
Автор: Gholam Reza Moghissi, Ali Payandeh
Журнал: International Journal of Information Technology and Computer Science @ijitcs
Статья в выпуске: 8 Vol. 11, 2019 года.
Бесплатный доступ
The hardness assumption of approximate shortest vector problem (SVP) within the polynomial factor in polynomial time reduced to the security of many lattice-based cryptographic primitives, so solving this problem, breaks these primitives. In this paper, we investigate the suitability of combining the best techniques in general search/optimization, lattice theory and parallelization technologies for solving the SVP into a single algorithm. Our proposed algorithm repeats three steps in a loop: an evolutionary search (a parallelized Genetic Algorithm), brute-force of tiny full enumeration (in role of too much local searches with random start points over the lattice vectors) and a single main enumeration. The test results showed that our proposed algorithm is better than LLL reduction and may be worse than the BKZ variants (except some so small block sizes). The main drawback for these test results is the not-sufficient tuning of various parameters for showing the potential strength of our contribution. Therefore, we count the entire main problems and weaknesses in our work for clearer and better results in further studies. Also it is proposed a pure model of Genetic Algorithm with more solid/stable design for SVP problem which can be inspired by future works.
SVP, Lattice reduction, Lattice based cryptography, Evolutionary Search, Genetic Algorithm, Parallelization, Graphic card
Короткий адрес: https://sciup.org/15016376
IDR: 15016376 | DOI: 10.5815/ijitcs.2019.08.02
Текст научной статьи A parallel evolutionary search for shortest vector problem
Published Online August 2019 in MECS DOI: 10.5815/ijitcs.2019.08.02
Lattice-based cryptography is the prominent candidate in post-quantum cryptography (secure cryptography against the quantum computers) [1]. Lattice theory entered in cryptography by the breakthrough paper of Ajtai [2]. The security in lattice based cryptography come from the hardness of the lattice problems, where SVP (Shortest Vector Problem) is the determinative one. In fact, since different lattice problems (which are the building blocks of lattice based cryptographic primitives) can directly or implicitly be reduced to SVP problem in most times, so the major attacks on this problem (SVP), consequently threaten these cryptographic constructions.
The NP-hardness of exact SVP was known at first for infinite norm in 1981 [3] and then, in 1998, for norm 2 (and any norm of p) under randomized reductions [4]. In other side, NP-hardness of approximate-SVP for constant factor (typically у = V2 ) proved in 2001 [5] and currently it is proved for у = 2(10gn)1 £. Also it is shown that, the approximate-SVP for factor of у = V^ , is belonged to PP A co- PP , and for factor of у = 2nl о g iо g n/iо g n is belonged to P. Also the smallest factor for cryptographic constructions is 0 (n) .
In solving SVP, lattice enumeration in a parallelepiped/ellipsoid bounded region of Euclidean space is the standard method. Lattice enumeration is the fastest algorithm in theory and practice for solving exact-SVP within the polynomial space methods. The enumeration time is affected by preprocessing the lattice block, and best theoretical result in this scope get by Kannan’s algorithm (with time complexity of 2o(”log”/2e) [6]) which improve for practical use in [7]. Besides the preprocessing, other effective practices for runtime of enumeration algorithm are suitable order of lattice points to be enumerated [8], and using the various pruning techniques [9]. Lattice reduction is other SVP solver which is often the fundamental technique which included in various lattice attacks. Some of the lattice reduction algorithms include: LLL reduction, BKZ reduction [8,10], slide reduction, HKZ reduction, BKZ 2.0 [11], progressive-BKZ [12]. The combinatorial methods are other techniques in solving SVP which in some parameters do better than lattice reductions [1]! Voronoi cell algorithm is theoretically one of the fastest deterministic algorithm with time complexity of 0(22”) for solving SVP which needed exponential space of 0(2”) [13]. Using randomization by combinatorial algorithms, the time complexity of Voronoi cell improved to (2 ). Also, sieving is the fastest randomized method with time complexity of 0(2c,n) and exponential space for solving (almost) exact SVP. Two main types of sieve algorithm are classic sieve and list sieve. Best improvement in provable version of sieve algorithm achieved the time complexity of о (2 ) by using combinatorial algorithms [14]. As we know, the best time complexity for heuristically (not-provable) sieving is о (2 292 ) [15]. Random sampling reduction is other technique for solving SVP which be investigated in lattice theory. Most of these algorithms can be used with other norms for solving other lattice problems (even by the same factor proved for SVP) such as closest vector problem, shortest independent vector problem. The well-known practical libraries which implemented some of these algorithms are NTL [16] and fplll [17].
Artificial Intelligence (AI) introduces some SVP solvers which look at this problem as an input hard problems which can be solved by general techniques of search/optimization. In an overall view, the general techniques can be classified in the search/optimization domain as follows: (I) the calculus-based search (such as Gradient decent, Newton method, Fibonacci method), (II) random-based techniques (such as evolutionary computations, statistical mechanics), and (III) the enumerative ones (such as back-tracking search, branch and bound, dynamic programing). Since the optimization/search methods introduced by AI to solve the hard problems, are often known with the class of randomly-guided searches, so our discussion will be focused on this class. In this paper, some main techniques in the class of randomly-guided search is briefly analyzed, including: evolutionary computations [18], statistical mechanics [19], fuzzy systems [20], neural networks [21] and fuzzy neural networks. By using some analysis, it is selected evolutionary algorithm as the best candidate in this class to design our SVP solver algorithm based on. Also, the special feature in our proposed algorithm is the tight combination of Artificial Intelligence with the lattice reduction theory and parallelization technologies.
Ding et al. propose a genetic algorithm for the first time in solving SVP based on sparse integer representations of short lattice vectors [22]. They suggest some heuristic techniques which improve their results [22]. In an independent work, Fukase et al. use orthogonalized integer representation in sampling technique to solve SVP [23]. These two papers introduce promising test results. In [24], it is proposed a new enumeration by integrating sparse orthogonalized integer representations for shortest vectors, also proposed a mixed BKZ method by alternately applying orthognalized enumeration and other existing enumeration methods. This methods [24] have exponential speedups both in theory and in practice for solving SVP. Although the results of using orthogonalized integer representation in solving SVP is so hopeful, but our approach in this paper is to use the plain representation of lattice vectors.
The remainder of this paper is organized as follows. A description of basic background on lattice theory is introduced in section II. In section III, it is made a so brief analysis on using different AI techniques to solve SVP. The parallelization considerations on multithreading technologies, graphic programming, and vectorization on CPU, described in section IV. We propose our parallel evolutionary search algorithm in section V. Also, a pure/novel model of Genetic Algorithm for SVP proposed in section VI, which we believe that it is a suitable candidate for further study. The experimental results and our analysis declared in section VII. Finally, in section VIII, the conclusion and further studies be declared.
-
II. Priliminaries
Lattices are discrete subgroups of ℝ which be defined by a basis. The bases are И -linearly independent vectors ^1 ,…, Ьн ∈ ℤ generating a lattice as follows:
-
ℒ( bl ,…, ьп )={∑ ^iXibt : ∈ ℤ} (1)
The number of independent vectors in lattice basis was known as rank of the lattice. The basis of lattice usually showed by matrix В . The volume of a lattice defined as absolute determinant of basis в . Also, the length of lattice vectors usually measured by Euclidean norm ‖ v‖2 which referred as ^2 norm and defined by:
-
‖V‖2= + 1V + ⋯ +V (2)
Many hard problems can be found in lattices, which SVP is one of the basic of them. For a given lattice basis, SVP defined as the problem of finding shortest nonzero vector in the lattice. The norm of best vector in lattice ℒ be shown by notation of ^1(ℒ). For practical purposes, the approximation version of SVP problem usually be used, which challenged to find a lattice vector with norm of at most some approximation factor У( п ) times the norm of the shortest nonzero vector. As be declared, many techniques introduced to solve SVP, where the lattice reduction is one of the main ones.
LLL is the most well-known lattice reduction algorithm which solve SVP with approximation factor of у ( п )=20( ) in a polynomial time. For a given basis в =( bi ,…, bn ) ∈ ℤ × , the parameter of 5 ∈ [1/4,1),
〈 b^,b ∗〉 the value of , = ∗ ∗ as a Gram-Schmidt coefficient and b ∗ as the i -th vector of Gram-Schmidt Orthogonalization in basis, the LLL-reduced bases should satisfy following conditions:
-
• Size condtion : | , |≤ for 1≤ j < i ≤ n
-
• Lovasz condtion : ‖ b ∗1-1 ‖2≥. 5 - Ц1+н /‖ b ∗‖2
Increasing the block size of 2 in LLL introduces BKZ algorithm which causes to better approximation factor of у ( n ) for SVP but takes more running cost. BKZ algorithm proposed by Schnorr in 1987. In other words, in LLL algorithm, it is tried to find the best norm in projected lattice block of dimension 2, while in BKZ algorithm, it is tried to find the best norm in projected block with dimension a ≥2.
Lattice enumeration algorithms are the main part of
BKZ reduction algorithm. For an input lattice block, the enumeration function aims to solve SVP. There are several practical improvements of enumeration algorithm collectively known as Schnorr-Euchner enumeration. Schnorr and Euchner proposed enumeration radii for pruning of enumeration tree [8], just based on some limited experiments. This pruning was analyzed by Schnorr and Horner [10] in 1995 which revised by Gama and et al. [9], who find flaws in it.
Gama, Nguyen and Regev [9] showed that a well-chosen high probability pruning (such as by Psucc ≥ 95%) introduces the speedup of 2 /4 over full enumeration [9], while their extreme pruning technique (such as by Psucc < 0.1% ) giving the speedup of (2-£) /≈ 1.414 over full enumerations. In fact, for block size of p and intermediate expected vector и (as a candidate of SVP solution), sound pruning replaces the inequalities of ‖ np-l+l ( и )‖≤ R for 1≤ I ≤ P by ‖ np-l+l ( и )‖≤ Ri ∗ R where 0≤ Ri ≤ ⋯ ≤ Rp =1. The vector of (■^"1 , ^*2 ,…, ^P ) named as bounding function which can be extreme pruned bounding function, or not-extreme one. The extreme pruned enumeration with bounding function ℛ˝ uses iterations of re-randomization,
Psucc (ℛ˝) , preprocessing and enumeration samples of the lattice block, where the best solution from all the iterations, returned as the final response. The pseudo-code of sound pruned enumeration function given at Appendix B from paper [9]. Note that, the most common technique to preprocess the lattice blocks before enumerations is the use of block reduction algorithms (such as BKZ). Also the initial enumeration radius R affects the enumeration cost, even though this radius is updated during enumeration [11] (in this paper, the selected enumeration radii is the one be introduced in [11] with radius parameter of √у).
-
III. Using Different AI Techniques to Solve SVP
Although exploring deeply the possibility of using the general techniques in the class of randomly-guided search/optimization for solving SVP, is beyond the scope of this paper, but it is discussed briefly this as follows:
systems and fuzzy neural networks may have some limited applications just in high level managing the SVP search techniques.
-
• Even though, some studies such as [19] show the possible application of statistical mechanics (by applying the metropolis algorithm for SVP problem) in solving SVP, but we found some main drawbacks in this work which encourage us to correct/improve them with a better underlaying search technique.
-
• Although the neural networks can be used for solving optimization problem, but in systematic process of designing a Hopefield network [21] for solving SVP with some standard design process, we found some main dificulties in the design steps!
As be declared, EA algorithm is selected for our design in section V. Also note that, all declared points on problems of using the different AI randomly-guided searches for solving SVP, are introduced based on our analysis when SVP be represented in its plain model, not other representations such as sparse integer representations of short lattice vectors.
-
IV. Parallelization Considerations
In this section, three technologies are described which be used to speed-up our proposed algorithm. These three technologies includes: MIMD (Multi-Instructions MultiData) technology by multicore-CPU, SIMD (SingleInstructions Multi-Data) technology by graphic cards, and Vectorization technology on CPU. In following subsections these technologies and their applications in this research be described.
-
A. MIMD technology by multi-threading over multi-core processors
MIMD technology on the multicore CPU introduces the ability of running inhomogeneous instructions over different data values. This technology implemented by multi-threading which be defined in user-level libraries (such as: POSIX Pthread, Mach C-thread, Solaris thread) and in the kernel of operating system (such as: Windows 95/98/NT/2000, Linux, Solaris). The user-level threads map to the kernel-level threads in three models of one-to-one, many-to-one, and many–to-many. These threads can be deleted whether in the states of asynchronous cancellation or deferred cancellation.
In practical implementation of block reduction algorithms (such as BKZ) on the large lattice challenges, the SVP oracles (enumeration function in BKZ) determines the total running time. Therefore the parallelization of block reduction algorithms focuses on the parallelism of these SVP oracles. In paper [26], the multi-threading approach is the balanced dedicating of enumeration branches in one enumeration tree to different processing threads for the maximum speedup. In paper [27], the multi-threading approach is massive run of so much threads which be dedicated to the extreme pruned enumeration samples over one lattice block. Also, newly a lattice basis reduction algorithm suitable for massive parallelization be proposed in [28] which experimental tests of this algorithm over SVP Challenges with dimension of 134, 138, 140, 142, 144, 146, 148 and 150, outperform previous world results which was the problem of dimension 132. Some considerations on using this technology in implementation of our proposed algorithm are as follows:
-
• The OpenMP standard be used to incorporate the MIMD in implementation of our algorithm (this standard uses Fork-Join model of parallelization).
-
• Thread mapping model in windows is one-to-one, in which that, every thread has an identification and independent thread context, including register sets, stacks and private data area (note that, our implementations in this paper introduced for windows platforms).
-
• Our implementation in this paper didn’t use the asynchronous cancellation of threads.
-
• The synchronization of the parallel threads is avoided as much as possible.
-
• No assumption on knowing the count of the available processors is used.
-
• The use of thread pools in the implementation of OpenMP in this paper is verified by some observed experimental evidences (note, the different implementations of OpenMP standards, don’t allow to access the internal thread pools).
-
B. SIMD technology by CUDA programming model
In November 2006, NVIDIA Inc. introduced CUDA (Compute Unified Device Architecture), a generalpurpose parallel computation platform and programming model for all NVIDIA GPU processors. In fact, CUDA is a graphics development environment [28]. The CUDA programming model makes it easier for programmers to use the GPU. CUDA supports various languages or APIs (Application Programming Interface) such as C, FORTRAN, OpenCL and DirectX Compute. In CUDA programming model, each thread can be identified by the block index (in the grid) and the thread index in the corresponding block. By identifying each thread, this thread can be dedicated to perform same operation on its specified data.
GPU hardware used more transistors than CPU to process data in SIMD mode [28]. The GPU hardware consists of several SM (Streaming Multiprocessors). The threads in the blocks of a SM run in groups of 32, called warp, in which that, at the same time execute the same instructions in SIMD mode. One of the main issues in warp is to avoid warp divergence (i.e., to maximize performance, it is needed to make sure every warp is fully active or completely disabled). Another main issue is that, if the number of needed registers exceeds the maximum number per SM, it may be used the L1 Cash or even device memory (in which that, this mechanism of registers distribution in different level of graphic cards memory architecture is not known exactly), so avoiding this problem, is one of the key issues in large-scale graphics applications. Also, the size of blocks in a SM has a non-negligible impact on the efficiency!
In some studies (such as [27]), the use of graphic cards for solving SVP were discussed. In the case of pruned enumeration function as SVP oracle, we faced with the worst scenario of warp divergence! So it cannot be expected that the pruned enumeration algorithms (such as Schnorr-Euchner pruned, Schnorr-Horner pruned and GNR 1 enumeration) achieve to the highest possible speedup by graphic cards! Other problems which we faced with, in using the graphic cards for solving SVP, are synchronization, overclocking, overheating, memory constraints and so on.
-
C. Vectorizing technology on CPU platforms
The vectorization technology is one of most notable concepts in performance analysis of current cryptographic constructions (see specification of NIST candidates at [38]). To have best practice for vectorization over CPU, assembly language should be used. Although current compilers (such as MSVC) try to apply highest optimization by auto-vectorization, but expert programmers when need to introduce some nontrivial speedup, they use the assembly language for vectorizing the critical section of codes [29]. Unfortunately, assembly language is non-portable for different hardware platforms, has maintainability problems, error-prone structure2, less flexibility and more cost in programming [30].
Since x86-mode dose not support last technologies in vectorization, the x64-mode should be used. The x64-mode assembly used flat memory model [29]. Some technologies which currently supported in CPU platforms are as follows [31]: SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2, AVX, AVX2 (256-bit band-width), AVX512 (512-bit band-width). Different assemblers support x64-mode, such as NASM, YASM, FASM and MASM [29], and finally the x64-mode MASM assembler (ML64.exe) is selected.
-
V. A Parallel and Evolutionary Search for SVP
In this section, different aspects of our proposed algorithm is described, which be named IEnum (Intelligent Enumeration). At first, it is discussed our search strategy for SVP problem in this algorithm. In the next sub-section, the details of our algorithm is described.
-
A. The search strategy in IEnum
In this paper, it is tried to collect the best approaches in AI (Artificial Intelligence), parallelization and lattice reductions into a single algorithm to get the best result. As be seen in Fig. 1, a loop of performing three steps is used, including: evolutionary search, brute-force of tiny full enumeration and a single main enumeration (in the next sub-section, the details of these steps are descibed).

Fig.1. High level strategy in IEnum search scheme
In the step of evolutionary search, we faced with a Genetic Algorithm which fully parallelized and reasonably used the knowledge of the lattice theory in its design. The step of brute-force of tiny full enumeration just be assumed as too much local searches with random start points over the vectors from the previous step. And finally, the step of main enumeration just is a pruned lattice enumeration on a preprocessed main block from the vectors of previous step.
The memetic strategy [29,30] was introduced by Richard Dawkins, which showed that the evolution not be limited to genes (Darwinian principal of natural evolutions). The concept of memetic comes from “mem”, which is a cultural element and transferring from one generation to next ones through non-genetic operations. In some views, the main features of memetic algorithm is the use of problem knowledge in different phases of evolutionary search. So it be seemed that, IEnum can be discussed in the context of a memetic algorithm, because of some features, including:
-
• Ability of preprocessing the population (such as by functions of AnttD ep endency , BKZ , LLL ) before different steps;
-
• Ability of using different lattice heuristic for search (over lattice blocks) and evaluation criteria;
-
• Using the problem knowledge in defining genetic operators;
-
• Using the local search (over a lattice block, not a single vector) to improve the children at each generation to get away from pre-mature
convergence;
-
• Ability to restart the population;
Algorithm 1 IEnum search
Input : =( bi ,…, bn ) ∈ ℤ × ,2≤ a , a ≤ p ≤ 71,1/4≤ 6 <1,
GSO Coef Mat p, enum radii param √у, ℛ, time[[m[t, GPUTNum, BEBS, maxN, deptℎ FullEnum , elitistMax, elitistMin, MaxElitistRound, elitistStep, BNB 1 bound , BNB2bound , ADTS, winSize
:
-
1: Timer _ Start ( timenmit );
-
2: Inititialize _ Params _ for _ CPU _ Side ();
-
3: Inititialize _ Params _ for _ GPU _ Side ();
-
4: Sort ( В ); // Sort В based on Euclidean norms ;
-
5: В ← A'^T-Dependency ( в ); n ← Rank ( В );
-
6: wℎ Ue (! Timer _ End ()){ // wℎ Ue 1
-
7: POP ← Crossover ( В , ∀ ( i , j ) ∈ В ) ⋃ В ;
-
// N = = ( POP );
-
8: Sort ( POP ); // worstVec = [ N ]; bestVec = [1];
-
9: ElitistRound =0; elitistNum = ;
-
10: wℎ Ue ( BNB 1< BNB 1 bound / ∗ or Ot ℎ erCriteia (…) ∗ /){
-
11: worstVec = [ N - n ];
maxN
-
12: Parentstdx =⋃ ( P( , Pi+i ) as parrent andices
from index array of
-
P = (1… N );
-
13: POP = ⋃ CrossOver ( POP , Parents );
-
14: Sort ( POP );
-
15: if ( POP [1]. norm < bestVec . norm ){
-
16: BNB 1=0; bestVM = [1];}
-
17: else BNB 1++;
-
18: if ( ElitistRound == ){
-
19: Ant tsimilarity ( POP , elitistNum );
-
20: ElitistRound =0; elitistNum =0;}
-
21: else ElitistRound ++;
-
22: topldx = ( worstVec . norm );
-
23: POP = ⋃ Cut elitistNum ( POP ) ⋃
Cut Reminder ( P ermuteRancl (Cut elitistNum+l ( POP )));
// Reminder = - n - elitistNum
-
24: if ( elitistNum < elitistMax ){
-
25: elitistNum += elitistStep ;
Reminder -= ;}}
-
26: POP = ⋃ Cut GPUTNum ∗ BEBS-n ( POP );
-
27: BNB 2=0; S2 ={};
-
28: w ℎ Ue ( BNB 2< BNB 2 bound / ∗ or Ot ℎ erCriteia (…) ∗ /){
-
29: Si ← BruteForceFuUEM ( PermuteRancl ( POP ));
-
30: $2 ←Cut winSize .Merge(S , AntiS(m(lar(ty ( Sort (51))/;
-
31: if ( Solutions [1]. norm < bestVec . norm )
-
32: bestVec = [1]; BNB 2=0; else BNB 2++;}
-
33: В ← AntiDependency ( Sort ( S2 ⋃ Cut ADTS ( POP ) ⋃ В ));
-
34: flock ← BKZa (Cut f ( в )); bestVM ← GNRp ( flock );
-
35: В ← Antij)epen(ienCy ( bestVec ⋃ В );} // end w ℎ Ue 1
-
36: delete _ Params _ for _ CPU _ Side ();
-
37: delete _ Params _ for _ GPU _ Side ();
-
38: Output : [1] //The output is the best vector of В
-
B. Detailed specification of IEnum search
The pseudo-code of IEnum search can be seen in Algorithm 1. Note that, it is clear that for performance issues, the implementation of this pseudo-code is more complex than our description in this sub-section, so for simplicity, other sub-functions and methods which be used for speeding up, are eliminated. Also since this algorithm massively uses the parallelization, we specify this in the algorithm by coloring the parallelized subfunctions (red color for CPU-side multi-threading and blue color for GPU-side parallelization). In the reminder of this sub-section, it is focused on details of Algorithm 1 by using a continuous organization.
Since a time bound is used to finally abort the algorithm, so at beginning of the code, a timer is set (line 1). Also since there are so much sub-functions in CPU-side and GPU-side which use many intermediate variables (such as vectors and Matrices), the definition and memory allocation of them should be used early in the algorithm for performance purposes (lines 2, 3). Note that, since in this algorithm, it is focused on the population of lattice vectors, so instead of Size condition, Lovasz condition and so on (see section II), the sorting of lattice vectors based on Euclidean norm is considered as the main technique for evaluation step (line 4). At this point, the rank of the lattice basis should be determined, so the function of AntiDepen(iency ( В ) is used for eliminating the dependent lattice vectors (line 5) which be implemented here by using the function of “IncrementalGS” in NTL library [16].
Now, the main loop of algorithm is performed which tries to improve the best norm of the solution after each round. The termination criteria of this loop determined by input time bound. This loop includes three main steps:
-
• Evolutionary Step
-
• Brute-Force of Tiny Full Enumerations Step
-
• Main Enumeration Step
Evolutionary Step :
In this step it is tried to use a smooth evolutionary search to maintain all possibilities (in lattice vectors) with moderate degree of being greedy. At first, the population is generated by using the basis vectors of B (line 7). The function of CrossOver ( В , ∀ ( i , j ) ∈ В ) performs crossover operation, simply by using add and minus over each two basis vectors, in a parallel SIMD way on the graphic cards (GPU-side), and finally produce Tl2 - n lattice vectors as parents (i.e., with basis vectors, the number of parents become Tl2 ). Note that, the norm of each vector is computed in the function of CrossO ver on GPU-side.
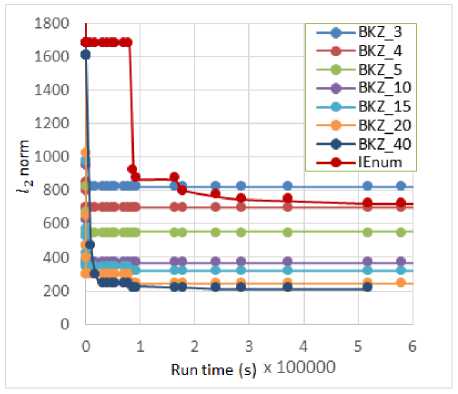
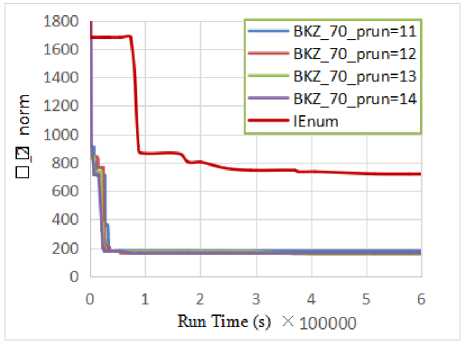
After that, the produced population POP is sorted based on Euclidean norm of vectors (line 8). To have best performance, a parallelized merge function (from mergesort) is used in our sorting algorithm on CPU-side. The termination criteria for the loop of this step (line 10) satisfied when the best norm in the population not be better (relating to the variable of BNB 1 ) after some specified number of generations (i.e., the violation of BNB1 Note 1: maxN is the maximum size of population which be assumed to be multiple of N. Note 2: The function of PermuteRand in the entire Algorithm 1 don’t collapse the sort of population, and just return an index array of uniformly random permutation of vector andices. In the way that the parents are generated, the number of maxN -N children are generated on GPU-side (line 12). Now, there is a population POP with size of maxN (line 13). Then this population is sorted in line 14 (parallelized in CPU-side). After sorting the number of maxN vectors in POP (line 14), the termination variable of BNB1 is updated in lines 15 to 17. Also the generations are allowed to have a bounded degree of elitism. The value of elitistNum show the current number of best vectors which can be presented directly in the population of next round of this step. By cutting the number of elitistNum from first (best) vectors in sorted population, implicitly the duplication (frequency) of best vectors be increased after each round, and consequently the chance (probability) of these vectors in parent selection be increased. To preserve the diversity, the elitist window (elitistNum) is reset after each number of MaxElitistRound rounds and the similar vectors is eliminated in the elitist window (vector index from 1 to elitistNum). As be seen in line 23, N vectors are selected for the next parents in POP , including basis vectors (for maintaining n independent vectors always in the population), elitist vectors, and N-n- elitistNum random vectors from the vectors of elitistNum+1 to the index of last vector (with norm of worstyec. norm ) in the sorted population. Finally, the elitist window size (i.e., elitistNum) can be increased up to elitistMax after each round by elitistStep (lines 24, 25). The rounds of this step continue the evolutionary search (a Genetic Algorithm) until the termination criteria (line 10) be satisfied and break the loop of the generations. Brute-Force of Tiny Full Enumerations Step: In this step, the degree of being exact in local search is increased, in the way that, a number of GPUTNum (GPU real Threads Number) from full-enumerations are performed with small block size of BEBS (Brute-force Enumeration Block Size) on random selected blocks from POP, instead of cross-over on two vectors. Note 3: The cross-over on two vectors can be assumed as a model of enumeration with the block size of two. Against the evolutionary search in pervious step, which children of a round can be parents of next rounds, in this step, we faced with completely independent enumerations on random selection of blocks from only last POP in previous step. The termination criteria be updated in lines 31, 32 and check in line 28 (similar to Evolutionary step, some other criteria van be used for termination). The function BruteForcepuiij?num run number of GPUTNum GPU thread for lattice enumeration in parallel. Since the lattice enumeration has so much unpredicted branches by structure of “if-else”, so a full enumeration tree with no prune for its branches is used! Also, since GPU cannot tolerate long continues sequence of operations, even with no branches, we limit the depth of enumeration tree with maximum depth which can be tolerated by the used Graphic cards. For our hardware platform in this paper, the enumeration tree depth is nearly 9 for all physical threads of used GPU (i.e., at each full enumeration tree with degree 3 on a real thread of our platform, 2∗3 = 13122 nodes be processed)1. For each selected random block, the GSO coefficients are computed fully parallelized on GPU-side, and consequently if the lattice block is not linear-independent (it can be found by using GSO information), this block can be eliminated from the spool of random lattice blocks before full enumeration. Finally in line 30, all the solution vectors are sorted at each round of this step (set s^), and eliminate the similar ones in this set, then this set (set s^ ) is merged with the last solutions in this step (set 5*2 ) to select the number of winSize first (best) vectors from the resulted set. Main Enumeration Step: In this step, it is tried to perform a pruned enumeration with small success probability of finding the shortest vector of a sorted block of the best independent vectors from previous steps. It is clear that, the success probability of this enumeration cannot be expected for high dimensional basis be reasonable (for p>200 )! Note that, in this research, a single sound pruned enumeration (GNR enumeration) [9] is used, not an extreme-pruned enumeration with re-randomization of the block. At first, the main block should be generated from the resulted vectors of the last previous steps. So the vectors from the set of $2 ,в and number of ADTS (AntiDependency Tolerable Size of population) from first vectors of POP is selected. The resulted collection is sorted, then he function of AntiDepenclenCy is performed over the sorted vectors. Then the first main block of resulted basis (with size of p) is preprocessed by BKZ reduction algorithm. A sufficiently big block size of a is used, while enumerations of BKZ parallelized on CPU-side, then performed a single sound pruned GNR enumeration with small success probability of finding SVP (which also parallelized on CPU-side). Note 4: since the function of ATltiDepg^g-^cy is fully sequential (and cannot be parallelized reasonably), we need to cut ADTS number of first vectors from POP . This algorithm continue until the timer reach to the time bound timellmlt . At the end of the algorithm, all the variables, vectors, and matrices which be defined and allocated on the GPU-side memory and CPU-side memory, should be deleted. VI. A Pure Model of Genetic Algorithm for SVP In this section, a pure model of Genetic Algorithm is proposed for SVP problem which we believed that it has more solid/stable design than IEnum. Against the IEnum algorithm, in this model, all the ordinary and standard concepts/techniques from Genetic Algorithm can be used. The principal difference is that, we use a combination operator, where different number of parents can be attended in the production of just one child, in which that this child is at least better than these parents! In fact, by accepting this operator as a combination operator in GA, we can re-define different techniques of parent selection, the elitism techniques, the selection of survivors, and so on. Against the IEnum algorithm, we don’t need to trim the population into n independent lattice basis vectors (i.e., in all the steps of this model, we faced with a population of lattice vectors, not a basis in some times). The pseudo-code of this algorithm is introduced in Algorithm 2. Algorithm 2 GA-Enum search Input: =(bi,…,bn)∈ℤ × ,2≤p≤n,1/4≤6<1, array of preprocess block size of aary, array of bounding functions ℛary, GSO Coef Mat p, enum radii param √у, : 1: POP ← Initialize_POP(В); //Size of POP is N 2: wℎUe(! Termination. Criteria()){// wℎUe 1 3: У(Convergence. Criteria()){ 4: POP ← Re_Initialize_POP(POP,В);} 5: plocksSet ← Parent. Selection(POP,p); 6: Combination Operator: Offspring =∅; ∀plock∈plocksSet do{ AntiDepeu(leucy(plock); P2 = . Size(); BKZ aary [ fe](plock, P2 ,8,ℛary 0O-ary[P2]1,R,√У); Vec ← GNRP1 (plock,ℛary [P2], R,√У); Offspring . Insert(Vec);} 7: Offspring. Evaluation(); 8: POP ← Survivor (Offspring∪POP) ;} 9: Output: . BestVec(); Here the Genetic functions of Initialize_POP(…) , Termination. Criteria(…), Convergence. Criteria(…), Re_Initialize_POP(…) and so on are used as the black boxes (except Combination operator). It is tried to clear the combination operator in this pseudo-code (line 6) to give a better sense of the algorithm, so different parts of this operator can be altered in further studies. Note that, in this operator, ℛ is an array of bounding functions for different block sizes and ^■ary is an array of preprocess block sizes for different main block sizes of j^2 . Note that, all the parallelization considerations in IEnum, can be applied in this model. VII. Exprimental Results and Discussion In this section, some experimental results are shown on running time and quality of output solutions in IEnum algorithm and be compared with the results of LLL and BKZ algorithms. The results were organized in 3 figures, which compared the Euclidean norm of IEnum output solutions with solution vector from LLL and BKZ algorithms. We believe that, using the lattice bases with small dimension (as be used in [19]) cannot represent the entire potential and strength of our contribution over the lattice reduction algorithms. By using LLL algorithm in polynomial time, the norm of best vector which be found, was limited by the bound of ≤20()Л1(ℒ). Also the use of polynomial-time BKZg which need to a limited block size of р, lead to the best norm of ≤20( /р) Л1 (ℒ) . Therefore, it is clear that, for small dimension of lattice basis, even LLL algorithm with parameter of б=3/4 may solve approximate-SVP, while for high dimensional lattice basis (which be used for practical secure cryptographic constructions), even the best variants of block reduction algorithms may not lead to sufficiently small norm of solutions! Therefore, we preferred to show the test results of our contribution for sufficiently high dimensional lattice basis. Consequently, against the results of [19], all the tests in this paper performed on randomized basis of Darmestadt lattice challenges [35] with dimensions of 300. This challenge re-randomized by a function inspired by “rerandomize_block(…)” in fplll library [17]. Table 1. Parameter set of IEnum for test results Parameter Value п (lattice basis dimension) 300 N n2 = 90000 maxN (integer times of N) 25∗N = 2250000 5 (LLL arg.) 0.99 а (preprocess block size) 40 р (main block size) 60 √У (radius parameter) 1.05 ℛ (bounding function) with success prob. of 50% timei(mtt ≈6000≈7 days BNB 1bound 400 BNB2 bound 2000 Number of blocks 13 Thread per block 1024 GPUTNum 13*1024=13312 BEBS 9 winSize 50 elitistMin 0.25 ∗N = 22500 elitistMax 0.75 ∗N = 67500 MaxElitistRound 30 elitistStep 18 deptℎFullEnum 9 All the implementations were compiled with MSVC x64 bit C++ (which tuned for high optimized output and auto-vectorization by SSE2), together with nvcc compiler. Host hardware platform (CPU-side) which be used, specified as follows: ASUS motherboard series Z97-K, Intel® Core™ i7-4790K processor with base frequency of 4 GHz, 16 GB RAM. Also the hardware platform in GPU-side specified as follows: GeForce GTX 970, MaxwellTM architecture, 1253 MHz base clock, 4 GB GDDR5 memory. Data types of RR and ZZ (in NTL library [16]) respectively be used for big real and integer numerical data. Also for better comparisons in diagrams, it is assumed that the termination conditions of BKZ and LLL algorithm are same which equal to time bound of 600000 s (≈ 7 days). The parameter set which be used for running of IEnum algorithm be shown in Table 1. In Fig. 2, the comparison of output norm (^2 norm) of IEnum (with parameter set which be introduced in Table 1) and LLL reduction with various parameters of 5 = 0.25, 0.5, 0.75, 0.99 is shown. This test result show that, IEnum always can be better than LLL reduction. Fig.2. The results of /2 norm for IEnum and LLL reduction algorithm In Fig. 3, the comparison of output norm (^2 norm) of IEnum and full-BKZ reduction (i.e., NTL BKZ with prun=0 ) with parameters of б = 0.99 , and various block sizes of р=3, 4, 5, 10, 15, 20, 40 is shown. This test result show that, IEnum (except for so small block sizes) may be worse than full BKZ reduction. Fig.3. The results of /2 norm for IEnum and full BKZ reduction In Fig. 4, the comparison of output norm ( ^2 norm) of IEnum and pruned-BKZ reduction with parameters of 6=0.99, block size ofр=70 , and various pruning parameter of prun=11, 12, 13, 14 is shown. This test result show that, IEnum may be worse than pruned-BKZ reduction with sufficiently big block sizes. Fig.4. The results of / 2 norm for IEnum and pruned BKZ reduction The slope of diagrams for BKZ (and LLL) algorithm verify this fact that, if BKZ algorithm is aborted after a polynomial number of SVP oracles over lattice blocks, then it was proved that the this output solution has the norm which slightly bigger than the output vector returned by fully finish of BKZ [36]. In other side, the slope of IEnum is smoother during the running time. VIII. Conclusion and Furture Studies The approximate-SVP within the polynomial factor directly or implicitly reduced to the security of many lattice-based cryptographic constructions, so achieving to these factors in polynomial time, break these constructions! In this paper, the best techniques of AI in general search/optimization combined with lattice theory techniques and parallelization technologies for solving the SVP. In the scope of AI, the possibility of using the general techniques in the class of randomly-guided search/optimization for solving SVP is briefly analyzed, and consequently EA is selected as the best candidate for our design. Then three technologies of multi-threading on multicore-CPU, graphic programming, and vectorization of program instructions is considered for implementation. By combining the knowledge of EA, parallelization and lattice theory, IEnum SVP solver is designed. IEnum algorithm uses a loop of performing three steps: evolutionary search, brute-force of tiny full enumeration and a single main enumeration. The evolutionary search, only is a Genetic Algorithm which fully parallelized and reasonably used the knowledge of the lattice theory in its design. The step of brute-force of tiny full enumeration just be performed in the role of too much local searches with random start points over the vectors from the previous step (inspired by memetic algorithms). Also, the step of main enumeration just is a GNR sound pruned lattice enumeration on a preprocessed main block of lattice vectors from the previous step. Besides our proposed algorithm, a pure model of Genetic Algorithm with more solid/stable design for SVP problem is proposed which can be inspired by future works. The test results showed that our proposed algorithm is better than LLL reduction in different parameters, but it may be worse than the BKZ variants (except some so small block sizes). We believe that, these test results is not sufficient for showing the entire potential strength of our contribution. Therefore, here it is tried to enumerate the possible further studies in the context of the problems and weaknesses of our work, as follows: 1. We believe that, our proposed pure model of Genetic Algorithm for SVP problem (Algorithm 2) in section VI, can lead to better results than our main algorithm (Algorithm 1), so we prefer to suggest this model to study and analyze more in the next researches. 2. We suggest that, in further studies, the parallelization considerations introduced in the level of super-computers or cloud (instead of low-level one, which be discussed in this paper), to have more practical view to parallel SVP solvers. 3. Since our contributions (in this paper) and the proposed algorithm in [19] defined their operations on pure lattice vectors (not projected lattice basis vectors), so these algorithms cannot be used as the SVP oracle for projected lattice blocks in block reduction algorithms (such as BKZ). 4. By using sufficiently high dimensional lattice challenges, our proposed algorithm cannot be tuned for optimized parameter sets, so the output results which be introduced in this section cannot fully represent the strength of our contribution. 5. The performance ratio of parallelization technologies used in proposed algorithm (in three classes which introduced in section IV) should be 6. We suggest that, for further studies other lattice challenges be used (such as SVP challenges in the sense of Goldstein and Mayer) in various dimensions. 7. Also we suggest that for further studies use other SVP solvers, such as slide reduction, Voronoi cell, sieve algorithms, RSR reduction and so on. Note 5: We believe that, it is a weakness in the step of brute-force of tiny full-enumerations in Algorithm 1, which introduced fully independent enumerations on random selection of blocks from only last POP, while in Algorithm 2, this full-independency be eliminated. Suggestion 1: It may be a suitable candidate to use orthogonalized integer representations of lattice vectors, for perform our proposed algorithm over projected lattice blocks (see [34]). Suggestion 2: We hope that this algorithm can be compete with BKZ reduction, by using the idea which introduced in section VI, and tuning the parameter sets of proposed algorithm to be optimized. Suggestion 3: For tuning the parameter sets of proposed algorithm, some techniques can be suggested such as: offline preprocess, offline/online neural network, fuzzy system and so on. compared to single thread and not-vectorized compiled code of the program (which can be test in further studies).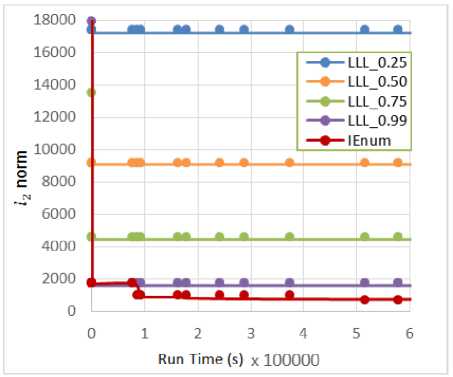
Список литературы A parallel evolutionary search for shortest vector problem
- Daniele Micciancio, Oded Regev, “Lattice-based cryptography”, In Post-quantum cryptography, pp. 147-191, Springer Berlin Heidelberg, 2009.
- Ajtai, M., “Generating hard instances of lattice problems”, In Complexity of computations and proofs, volume 13 of Quad. Mat., pages 1–32. Dept. Math., Seconda Univ. Napoli, Caserta (2004). Preliminary version in STOC 1996.
- P. V. E. Boas, “Another np-complete problem and the complexity of computing short vector in a lattice”, in Tech. rep 8104, University of Amsterdam, Department of Mathematics, Netherlands, 1981.
- M. Ajtai, “The shortest vector problem in l2 is np-hard for randomized reductions”, in STOC 98: Proceedings of the 30th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 1998, pp. 10–19.
- D. Micciancio, “The shortest vector in a lattice is hard to approximate to within some constant”, SIAM Journal of Computing, vol. 30(6), pp. 2008–2035, 2001.
- Hanrot, Guillaume, Damien Stehlé, “Improved analysis of Kannan’s shortest lattice vector algorithm”, In Annual International Cryptology Conference, pp. 170-186. Springer, Berlin, Heidelberg, 2007.
- D. Micciancio, Michael Walter, “Fast lattice point enumeration with minimal overhead”, In Proceedings of the twenty-sixth annual ACM-SIAM symposium on Discrete algorithms, pp. 276-294. Society for Industrial and Applied Mathematics, 2014.
- C. P. Schnorr, M. Euchner, “Lattice Basis Reduction: Improved Practical Algorithms and Solving Subset Sum Problems”, Math. Programming, 66:181–199, 1994.
- N. Gama, P. Q. Nguyen, O. Regev, “Lattice enumeration using extreme pruning”, In Proc. EUROCRYPT ’10, volume 6110 of LNCS. Springer, 2010.
- C.-P. Schnorr, H. Horner, “Attacking the Chor-Rivest cryptosystem by improved lattice reduction”, In Proc. of Eurocrypt ’95, volume 921 of LNCS, Springer, 1995.
- Yuanmi Chen, Phong Q. Nguyen, “BKZ 2.0: Better lattice security estimates”, In International Conference on the Theory and Application of Cryptology and Information Security, pp. 1-20. Springer Berlin Heidelberg, 2011.
- Y. Aono, Y. Wang, T. Hayashi, T. Takagi, “Improved progressive BKZ algorithms and their precise cost estimation by sharp simulator”, In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 789-819. Springer, Berlin, Heidelberg, 2016.
- Micciancio, Daniele, Panagiotis Voulgaris, “A deterministic single exponential time algorithm for most lattice problems based on Voronoi cell computations”, SIAM Journal on Computing 42, no. 3 (2013): 1364-1391.
- Aggarwal, Divesh, Daniel Dadush, Oded Regev, Noah Stephens-Davidowitz, “Solving the shortest vector problem in 2^n time using discrete Gaussian sampling” In Proceedings of the forty-seventh annual ACM symposium on Theory of computing, pp. 733-742. ACM, 2015.
- Anja Becker, Leo Ducas, Nicolas Gama, Thijs Laarhoven, “New directions in nearest neighbor searching with applications to lattice sieving”, In Robert Krauthgamer, editor, 27th SODA, pages 10-24. ACM-SIAM, January 2016.
- Victor Shoup, “NTL vs FLINT”, available at http://www.shoup.net/ntl/benchmarks.pdf.
- GitHub hosting service, fplll library project, available at https://github.com/fplll/.
- Eiben, Agoston E., James E. Smith, “Introduction to evolutionary computing”, Vol. 53. Heidelberg: springer, 2003.
- Shenoy, K. B. A., Somenath Biswas, Piyush P. Kurur, “Metropolis algorithm for solving shortest lattice vector problem (SVP)”, Hybrid Intelligent Systems (HIS), 2011 11th International Conference on. IEEE, 2011.
- Oltean, Gabriel, “Fuzzy Techniques in Optimization-Based Analog Design”, WSEAS International Conference, Proceedings. Mathematics and Computers in Science and Engineering. Eds. W. B. Mikhael, et al. No. 10. World Scientific and Engineering Academy and Society, 2008.
- Hopfield J., Tank D., “Neural Computation of Decisions in Optimization Problems”, Biological Cybernetics, Vol. 52, pp 141-152, 1985.
- Ding D, Zhu G Z, Wang X Y., “A genetic algorithm for searching the shortest lattice vector of SVP challenge”, In: Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, 2015, 823–830.
- Fukase M, Kashiwabara K., “An accelerated algorithm for solving SVP based on statistical analysis”, J Inf Process, 2015, 23: 67–80.
- Zhongxiang Zheng, Xiaoyun Wang, Yang Yu, “Orthogonalized lattice enumeration for solving SVP”, Science China Information Sciences 2018.
- Aono, Yoshinori, Phong Q. Nguyen, Yixin Shen, “Quantum lattice enumeration and tweaking discrete pruning”, International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2018.
- Fabio Correia, Artur Mariano, Alberto Proenca, Christian Bischof, Erik Agrell, “Parallel improved Schnorr-Euchner enumeration SE++ for the CVP and SVP”, In 24th Euromicro International Conference on Parallel, Distributed and Network-based Processing, 2016.
- Kuo, Po-Chun, Michael Schneider, Özgür Dagdelen, Jan Reichelt, Johannes Buchmann, Chen-Mou Cheng, Bo-Yin Yang, “Extreme Enumeration on GPU and in Clouds”, In International Workshop on Cryptographic Hardware and Embedded Systems, pp. 176-191, Springer Berlin Heidelberg, 2011.
- T Teruya, K Kashiwabara, G Hanaoka, “Fast lattice basis reduction suitable for massive parallelization and its application to the shortest vector problem”, PKC 2018: Public-Key Cryptography – PKC 2018 pp 437-460
- “CUDA C Programming Guide”, eBook, NVIDIA Corporation, available at www.nvidia.com, July 19, 2013.
- Chris Lomont, “Introduction to x64 Assembly”, Intel® Corporation, available at https://software.intel.com/sites/default/files/m/d/4/1/d/8/Introduction_to_x64_Assembly.pdf, February 27, 2014.
- Ray Seyfarth, “Introduction to 64 Bit Windows Assembly Programming”, eBook, CreateSpace Independent Publishing Platform, October 6, 2014.
- Chris Lomont, “Introduction to Intel® Advanced Vector Extensions”, Intel White Paper, 23 May, 2011.
- Guide, P., “Intel® 64 and IA-32 Architectures Software Developer’s Manual”, Intel® Corporation, available at http://download.intel.com/design/processor/manuals/253665.pdf, Vol.1, May 2011.
- Auger, Anne, Benjamin Doerr, “Theory of randomized search heuristics: Foundations and recent developments”, Vol. 1. World Scientific, 2011.
- Ong, Yew-Soon, Meng-Hiot Lim, Ning Zhu, Kok-Wai Wong, “Classification of adaptive memetic algorithms: a comparative study”, IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 36, no. 1: 141-152, 2006.
- R. Lindner, M. Ruckert, “TU Darmstadt lattice challenge”, available at www.latticechallenge.org.
- G. Hanrot, X. Pujol, D. Stehle, “Analyzing blockwise lattice algorithms using dynamical systems”, In Proc. CRYPTO ’11, LNCS. Springer, 2011.
- “Implementing Bubble Sort with SSE”, available at http://www.codeproject.com/Articles/23558/Implementing-Bubble-Sort-with-SSE.
- NIST post-quantum candidates, available at https://csrc.nist.gov/Projects/Post-Quantum-Cryptography.


