A parallel soft computing model for identifying lost student in an incomplete and imprecise environment
Автор: Mahendra Kumar Gourisaria, Susil Rayaguru, Satya Ranjan Dash, Sudhansu Shekhar Patra
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 4 vol.10, 2018 года.
Бесплатный доступ
The numbers of educational institutions are growing at par with the lost student rate in a country like India. When a missing student is found we need to identify the student on the strength of some common parameter like student name, his/her institution name, branch or class etc. But we never get accurate and complete information in most of the cases to identify or recognize a lost student. In such a situation, a soft computing model can be a striking choice to track a lost student on the basis of partial information. In the past we propose soft computing model for the same. This paper proposes a more optimized parallel soft computing model which takes half of the time taken by the earlier single thread model for identifying a lost student on the basis of imprecise and partial information. The system is tested meticulously on a database of 50000 records and an efficiency of 94% is obtained.
Soft computing, parallel soft computing model, symbolic similarity measure, fuzzy theory and lost student tracking
Короткий адрес: https://sciup.org/15016481
IDR: 15016481 | DOI: 10.5815/ijisa.2018.04.07
Текст научной статьи A parallel soft computing model for identifying lost student in an incomplete and imprecise environment
Published Online April 2018 in MECS
Identifying or recognizing a lost student is a most vital, laborious and time consuming task especially when the available information about the lost student are inaccurate, imprecise and partial. Hence in such an atmosphere a parallel model of soft computing will be of very useful and faster when the complete information of the student is not available. It becomes a Herculean task to identify a lost student especially when the data set or knowledge base is overwhelmingly large. Hence a parallel model is very useful which can also reduce the time complexity. The job of recognizing a lost student involves categorization and classification of textual information. Text categorization is the job of categorizing to free-text documents base on their content [1][3][15].
This paper is proposing a parallel model of soft computing for identifying a lost student which normally takes student information as input and identifies the lost student in minimal time. The proposed system model is depicted in Figure 1.
This model requires proper illustration of student information. The feature of lost student like inappropriate and impreciseness data and non-existence of a variety of field make it suitable for representing it as a Symbolic Object [4] which is further processed by using a method called similarity measure to recognize the lost student. This likeness measure assigns different similar values to find out the closeness of the lost student to different student object present in the knowledge data base. Therefore this measure is similar to fuzzy membership function. We have tested this model using a knowledge base of 50000 student objects and found that overall 94% of accuracy is achieved.
Basically Symbolic objects are extension of classical data types which are of three dissimilar types, the first one is assertion object, second is hoard object, and the third is synthetic object [6][11]. An assertion object is a combination of events relating to a specified object [12][13]. An event is nothing but a couple which associates feature variables and feature values. On the other hand, a hoard object is defined as a group of single or extra assertion objects, while a synthetic object is nothing a collection of single or extra hoard objects [5].
The rest of the paper is organized as follows. Section 2 deals with symbolic object and explains how student information can be represented as symbolic object. Section 3 presented a parallel fuzzy model for tracking lost students. Section 4 explains about the symbolic knowledge base for labeling of student component and student identification.
Input Student Detail
Fig.1. Bearings-only measurements in clutter
Section 5 describes symbolic similarity measure. Section 6 presents a fuzzy alpha cut methodology for conveying value of confidence for the recognized student. Section 7 presents the experimental results. Section 8 is concluding the paper.
-
ii. Representation of Student Information as a Symbolic Object
Identification of a lost student exclusively depends on the correctness of the information like name of the student, institution name, and address where the student studies, class or branch of the student etc. In this case any computational model has to deal with approximate or incomplete student information where some of the field value may not be accurate or missing. Hence the soft computing model is an appropriate choice. Here the same data structure can be applied for representing the knowledge base. As a few of the fields are qualitative for instance student name while others are numeric in nature such as age, hence we are applying a symbolic data approach to represent the student information
The symbolic representation of object [7] is a helpful particularly for object having diverse and changing number of fields and matching data and knowledge bases. As we have already told that the Symbolic objects of three types. The graphical representation of the classification of symbolic object and their relationship is depicted below in Figure 2.

Fig.2. Classification of Symbolic Object and their relationship
In this paper, Student object is expressed as a hoard object which is a combination of three assertion object as student information, institution location, and institution place as depicted in equation (1):
Student object = {[Student Information, Institution Location, Institution Place]}.
In equation (1), Student information specifies all the student details pertaining to the lost student like name, age, gender, class or branch, etc. Institution location denotes the physical location of the institution and institution place denotes the town/city or village name where the institute is situated. Assertion objects are the combination of different events and each event are again combination of feature variable and value. The feature variable of student object is listed in equations (2) to (4).
Student Information = (Name)(Age)(Gender)(Class) (Roll Number)
Institute Location = (Name)(Plot Number)(Road)(Area Name)(Pin No)
Institute Place(Post)(District)(State)(Place) (4)
Table 1. A Typical Student Obejct
|
Lost Student Information |
Symbolic Student Object |
|
Name: Ajit Paul |
StudentObject ={ |
|
Age:17 |
|
|
Gender:Male |
[Student = (Name=Ajit Paul),(Age=17), |
|
class:9th |
(class=9th) ,(RollNumber=87)] |
|
RollNo:87 |
[Location = (Name=Ramkistopur Kendriya |
|
School: Kendriya Vidyalaya |
Vidyalaya),((Area=Ramkistopur)(Pin=751019)] |
|
RamKistopur, Cuttack,Orissa |
[Place=(City=Cuttack),(State=Orissa)] |
|
Pin-751019 |
} |
-
III. A Parallel Soft Computing Approach
Soft Computing basically constitutes of fuzzy logic, artificial neural network and Genetic Algorithm has become one of the most important research and application fields for computer science in the last decade.
Generally for optimization problem, we use soft computing approach. It is well known that when we talk of human bias or even proximity to a perfect value, the most excellent relative way of modeling this type of circumstances is by way of fuzzy sets, or more generally with soft computing methodologies. In this paper we have applied a parallel soft computing approach for tracking lost student information [14][16].
A. A Parallel Fuzzy Model for Identifying a Lost Student
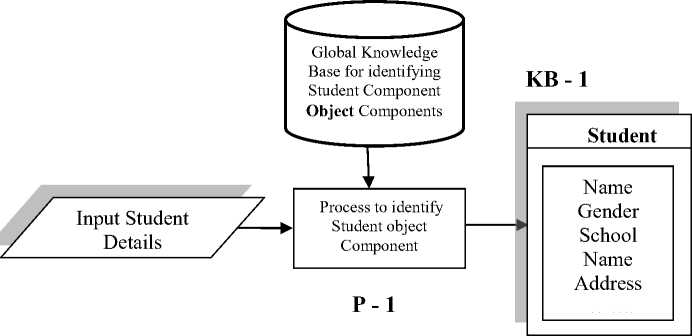
Identification of a lost student based on imprecise information requires human expertise. This entails a fuzzy model to be developed for tracking the lost student with inappropriate information. The fuzzy model basically comprises two things, first a knowledge data base and second an inference engine for the purpose of simulating individual expertise. The entire process of tracking the lost student can be divided into two phases. In the first phase the student object is created based on the student information, in this phase manual entry of student information is made. In the second phase the lost student is tracked with the Symbolic Student Object generated in the first phase. Figure 3 illustrate the schematic diagram of the parallel fuzzy model devised for identifying the lost student.
Process to track Student based on Student object and Student Knowledge
Base Parallely

Tracked Student
P - 2
MAC -1
MAC -2
MAC - N
Student
Knowledge Base
KB - 2
Fig.3. A Parallel Fuzzy model for identifying the lost Student
In the above parallel fuzzy model, student information is supplied to the first process – P-1 which as a result generates the student hoard object and recognizes different student components like name, age, and school etc. of the student object. Process P-1 also looks up the knowledge base KB-1 for identifying and labeling different student components and employs symbolic similarity measure which is a kind of fuzzy membership function. We have also devised fuzzy alpha cut set for allocating a confidence value in this process on the basis of similarity measure to the identified student object.
After the student object is generated, it is passed on to the next process – p2 which in turn pass it to multiple clients who compared or mapped the object in parallel with all the student information available in the KB-2 and employed the symbolic similarity measure function to locate the fuzzy space of the input student information and the different likely student records.
-
IV. Symbolic Knowledge Base
As per our proposed model as depicted in the Figure 3 there are two knowledge bases, one for identifying student component described in section A for generating the student object and another for parallel mapping the student object to the probable student record described in Section B .
-
A. Symbolic knowledge base for labelling and identification of student component
The symbolic knowledge base utilized for identifying student component, STD_COMP_KB acts as a repository of student information that will assist in labeling student components. This knowledge base is structured as a synthetic object which comprises of three different hoard objects and again the hoard object are made of assertion objects as given in the following equation (5).
STD_COMP_KB =
{ [Stdudent_Kb],[Location_Kb],[Place_Kb]}
STD_COMP_KB
Stdudent_Kb = { [Name] [Care of] [Class] [Roll No] [Gender] [Blood
Group]
}
Location_Kb = { [School Name] [PlotNo] [Area Name] [Land Mark] [Pin]
}
Place_Kb={
[District] [State]
[Country]
}
Fig.4. Structure of Student Component Knowledge Base
When the student information is supplied to the process (P-1), it breaks the student information into different input component and each of the components is thoroughly compared with the entire event present in each of the assertion object and assigns a similarity measure value. The comparison which has got higher similarity values is labeled with compared event.
-
B. Knowledge base for student identification.
Once the student object is generated based on the input details, it is compared with the Student_Knowledge_Base for recognizing the lost student. This has been created by considering huge quantity of student information and the variant of ways the student information can be represented. The symbolic knowledge base is structured like a synthetic object:
STUDENT_KNOWLEDGE_BASE comprising of three hoard object which in turn contains the assertion object as given by equation (6).
Student_Knowledge_Base = {[Std_Map_AddressKb],[std_Map_Location_Map_Kb],[ std_Map_PlaceKb]}
STUDENT_KNOWLEDGE_BASE

Std_Map_AddressKb = { [ID NO] [Name] [Class] [Roll No] [Gender] [Blood Group] } std_Map_LocationKb = { [ID NO] [School Name] [PlotNo]
[Area Name] [Land Mark] [Pin] }
Std_Map_PlaceKb={ [ID NO] [District] [State] [Country] }
Fig.5. Structure of Symbolic Student Knowledge Base
Each record present in different assertion object is represented by a unique ID No. This ID No acts as a link in between the records present in different assertion object. For each assertion object, one or more value is stored in the knowledge base under one ID No. This symbolic knowledge base is utilized to map the Symbolic Student Object to a possible student record.
V. Symbolic Similarity Measure
The characteristic of lost student information like impreciseness, the existence or non-appearance of a variety of fields makes the symbolic data demonstration a suitable choice. This approach for student component labeling and identifying lost student requires similarity measures to map the input data to different student components for generating the student object and mapping the student object to probable student record present in the knowledge data base. Similarity/distance measure classifies [9] the data to a set of predefined target groups or elements according to the nearness to a particular target element. The similarity measure can be categorized into three types as position similarity, content similarity and span similarity. For interval type of data, we generally use position similarity. The span similarity can be utilized for both type of data i.e. interval type and absolute type. The content likeness explains the likeness between the stuffing of the two objects [10]. The similarity procedures defined in [8] have been utilized for classification and clustering etc.
-
A. Symbolic similarity measure for labeling of student component
The categorization of student information as input into student label component needs the application of techniques of categorization of text [2]. This similarity calculation provides the likeness value of the enter component with a variety of component labels of the symbolic synthetic object STD_COMP_KB. The likeness measure stuck among ith keyin component (IPa) and jth component label (CLb) of the knowledge data base is established by equation (7).
SM(IPa,CLb) = netSim for 1<=a <= p and 1<= b <= o, where p is the quantity of on hand components , o is the quantity of probable component labels in the knowledge base. The values of netSim are calculated as per equation (8) for the initial five to compute content likeness and equation (9) for the final two to compute span and content likeness:
Interse wfk x------------- k Sum _ IP _ KB
1 <= o <= 5
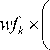
Interse --+
Sum _ IP _ KB
Comp IP + Comp KB 2 * Sum _ IP _ KB
6 <= o <= 7
here Interse is the quantity of words common to enter component under test, the quantity of elements in the input component is shown by Comp_IP , the quantity of words in the component label (knowledge base) is shown by Comp_KB and Sum_IP_Kb is equal to the sum of Comp_IP and Comp_KB minus Interse .[11][13]
The wf k which is the weight factorsare already defined for all label and the values are allotted on the basis of the relative significance of the events in dissimilar labels (assertion objects). Then we compute the similarity measures which are the fuzzy membership function. The real judgment where the input components belongs to which label class is made using the defuzzification method which is described in Section VI- A.
-
B. Identifying lost Student based on the student object using symbolic similarity measure.
For recognizing the lost student based on the student object we need to compare the different assertion object of the symbolic student object with the corresponding assertion object of the knowledge base and needed to assign a similarity value. Let the input student object is represented by S´. Student symbolic object has got three assertion object components symbolized as S´S (student assertion object), S´L(location assertion object) and S´P (place assertion object).
S´ = {S´S, S´L, S´P} (10)
Let every record in the student knowledge base (hoard object) be characterized by Sk i and information in the location knowledge base be symbolized by Lk j and each record in the place knowledge base be characterized by PKk, for all 1≤ i ≤ m , 1 ≤ j ≤ n and 1 ≤ k ≤ o where m is the amount of entries in the student knowledge base, n is the number of entries in the location knowledge base and o is the quantity of entries in the place knowledge base. The similarity component that calculates the student similarity gives the closeness of the input student assertion object S´S with a variety of student information present in the symbolic hoard object Std_Map_Kb using the equation (11)
EC
S ( S ' S , SK ) =--- £ netsim (11)
EC p = t p
In the above equation we are comparing the similarity measure between the input student assertion object S´S and each entry SKi present in the hoard object Std_Map_Kb, where EC is the quantity of components of the student assertion object already there in the input. The value of netsimp (net similar measure) for each component is work out in (12) with respect to student information present in the Std_Map_Kb.
scanSimp + contentSimp netsim n = -------------------------- (12)
p 2
The parameter scanSimp p and contentSimp p stand for the span similarity and content similarity measure for student identification mapping which are computed as in (13) and (14).
scanSim
comp PO + comp KB
2* Sum PO KB
where Comp_PO is the count of words in the component, the quantity of words in the repository of knowledge base entry Sk i is represented by Comp_KB and Sum_PO_KB is obtained after adding Comp_PO and Comp_KB -Interse; where Interse = COM * MF and COM = quantity of words common to S´S and Sk i . MF = 1. When all word of S´S and Sk i are matches and MF = k/n. When k words of the n possible words of S´S matches.
contentSimp =
Interse
Sum PO KB
In the same way, similarity measure among key in location information and location object of the knowledge base is calculated as per equation (15).
S ( S ' L , LK, ) = — ETn netsim (15)
ECpix p where EC is the quantity of component of student location object already there in the input. In the same way we can compute similarity between place information and place object of the knowledge base using equation (16).
EC
S ( S ' P , PK) = — £ netsimp, (16)
EC p = 1
where EC is the number of component present in the place assertion objects already there in the input S. Now the similarity measure for a given student record present in the Student Knowledge Base can be computed taking all the above three similarity measure in to account. Here first the student object is generated, and then the labeling is completed and finally the mapping is done in parallel with std_map_AddressKB, std_map_LocationKB and
S ( S ' S , KB ) =
S (S' S, SKi) + S (S' L, LKi) + S (S' S, PKi) Sum PO KB std_map_PlaceKB and sends the result to the client which is depicted in the Figure 6 as follows:
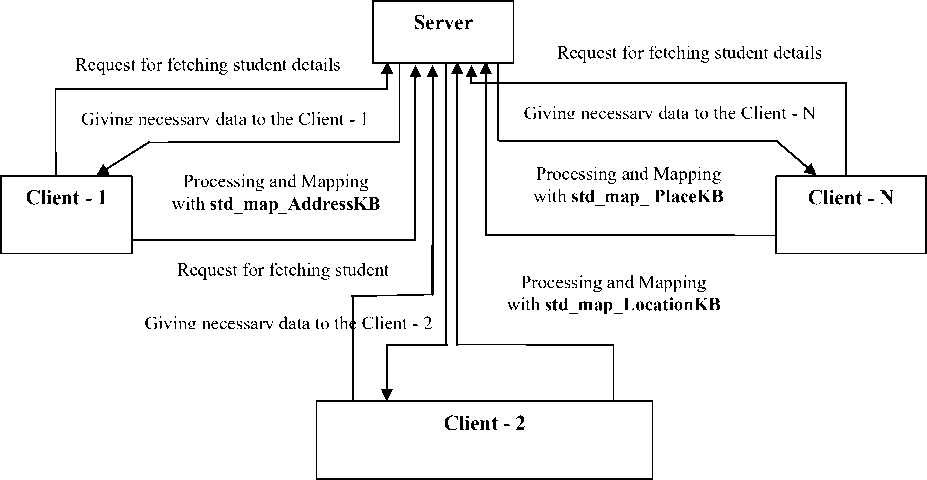
Fig.6. Structure of the overall parallel mapping of the entire Database
-
VI. Fuzzy Decision and Confidence Value
The symbolic similarity measures, which we have calculated as per Section 5, are again defuzzified to eliminate the vagueness in making a decision upon the component labels. We have applied alpha cut tactic for defuzzification which is described in Section VI.- A . Section VI- B presents the method engaged for defuzzification.
-
A . Student Component Labeling
Before the generation of the student object, the input student components are accumulated in a data structure called Student Component Information Structure (SCIS)
as per Table II. At a single point of time only one component is kept in SCIS. SCIS subject to go on rigorous similarity measure evaluation with the entire component label present in the Std_Comp_KB knowledge base. After the computation of the symbolic similarity measure using equation (7), the component labels are organized in the declining arrangement of similarity. This list provides the fuzzy membership of the key in component in the probable labels.
Now we require a process of defuzzzificaiton and the alpha value is calculated using equation (18)
a = S o _ DFC * So (18)
here S0 shows highest likeness value acquired for the input component, and DFC is the defuzification constant which is considered as 0.1, on the basis of experiment with student components. After commuting the α value we need to consider the probable component label present in SCIS which has got the similarity value grater then the α value and store the components in a similarity sorted array as depicted in Table III.
Table 2. Student Component Information Structure
|
Input Component |
Probable Component Label |
Similarity Measure |
|
IC 1 |
C 1 |
S 0 |
|
IC 1 |
C 2 |
S 1 |
|
IC 1 |
C 3 |
S 2 |
Table 3. Student Component Information Structure
|
Index |
I 0 |
I 1 |
I n |
|
|
Similarity Measure |
S 0 |
S 1 |
S n |
|
|
Component Label |
C 0 |
C 1 |
C n |
The alpha cut set is utilized to recognize the component label with allocated confidence value for the judgment. The confidence of each component is computed as given in the equation (19).
Con a , b
*100 for 1 ≤ b ≤ c and 1 ≤ a ≤ n (19)
C Sk k =1
Where Cona,b is the confidence of allocating bth component label to ath input component, n is the quantity of input component and c is the quantity of component labels in alpha cut set, S b is the similarity for the ath input component with the bth component label in similarity array[11][13]. S k is the similarity for the ith input component with the kth component label in the similarity array.
Algorithm1: Student component labeling and Student Object generation.
Input: Student Information for tracking
Output: Student Object based on the input student details.
Begin
-
1. Input student information
-
2. Partition the student information into different component (as present in different line or separated with comma) and keep the components in an array (compArray).
-
3. For i=1 to lengh[compArray] do
-
3.1 Fetch the ith input component from the compArray
-
3.2 Compare the component with all the component label present
-
-
3.3 Store the probable component label with the similarity measure in SCIS.
-
3.4 Defuzzify the component label with by defining fuzzy alpha cut set.
-
3.5 Label the input component with appropriate component label.
-
4. Generate Student Object based on the labeled input component.
in the hoard object (std_addresskb,std_locationKb,std_placeKb) of the knowledge base Std_Comp_Kb and compute the similarity measure.
End For.
End
-
B. Student Identification based on the generated student Object
The labeled student components are structured as a student object, which is then mapped with the entire symbolic student object there in the Knowledge Base. It is possible that one student object can be mapped with more than one symbolic object present in the Std_Knowledge_Base. In such situation we need to provide confidence value for each mapping, which can be carried on by defuzzification by applying fuzzy alpha cut set methodology.
Alogorithm2: Identifying the lost student based on the student object in parallel
Input: Symbolic Student Object
Ouput: Identified student based on the input student object.
Begin
Client 1 ……..Client N request for the symbolic student object.
Server sends back the requested student object to different Client’s.
All the clients will run in parallel to find the similarity measure of the Student Object with the knowledge Base which includes std_map_AddressKB, std_map_LocationKB, std_map_PlaceKB.
Each client will sent back the similarity measure of the student object to the server.
Server will find the sum of all the three similarity measure and sort them in descending order.
Server will perform the alpha cut operation and If only one match lies in the alpha cut set, then output the symbolic student present in the knowledge base with 100% confidence value.
If more than one symbolic object lies in the alpha cut set then compute the confidence value accordingly. The symbolic student objects with the confidence value are output.
End
-
VII. Experimental Results and Debate
This parallel proposed model for student identification is meticulously tested using the student knowledge base having more than 50000 student records. The experimental results for student component identification (Student Object Generation) are described in Subsection VII- A and the results for Symbolic Student Object parallel mappings with the knowledge base, i.e. the comparative study of sequential and parallel execution of the proposed model are presented in Subsection VII- B .
-
A. Labeling of Student Component
The proposed method for labelling of student component is tested on a variety of student information and the result is very much satisfactory. Table 4 depicts how the input component are identified and labeled with the help of similarity measure and alpha cut set methodology. Here we are showing the result of one student with his similarity measure computed with respect to the input components. After conducting a rigorous test we have observed the efficiency of the system is 94% in component labeling. The result shows that approximately all the components are accurately identified.
Table 4. Result of Student Component Identification
|
Input Student Details |
Identified Components |
Similarity Measure with label |
Similarity Measure with label |
Alpha cut set |
Confidence Of Decision |
|
Hariom Patra, |
Hariom Patra, |
.562,student name |
.231 , area name |
{Student name} |
100 |
|
class-10 |
class-10, |
.543 , class |
.245 ,roll number |
{Class} |
100 |
|
BG-AB+ |
BG-AB+, |
.509, B/G |
.117 ,plot no |
{B/G} |
100 |
|
Venkateswara |
|||||
|
English Medium |
Venkateswara |
.462 ,school |
.284 ,area name |
{School} |
100 |
|
School |
English Medium |
||||
|
Chandrasekharpur |
School, |
||||
|
Chandrasekharpur, |
.531 ,area name |
.161 ,student name |
{Area name} |
100 |
|
|
Bhubaneswar |
Bhubaneswar, |
.527 ,city |
.111 ,student name |
{City} |
100 |
|
Odisha |
Odisha, |
.493 ,state |
.238 ,area name |
{State} |
100 |
|
751016 |
751016 |
.592 ,pin100 |
.115 ,state |
{Pin} |
100 |
Table 5. The Result of the System Deal with Various Mapping Issues
|
SI No. |
Input |
Output – Client Wise |
Final Output to Server |
SM & Confidence |
Explanation |
|
1. |
Hariom Patra,class-10 BG-AB+ Venkateswara English Medium School Plotno-450 Chandrasekharpur Bhubaneswar Odisha 751016 |
Reply by Client – 1 – (Hariom Patra,class-10, BG-AB+) Reply by Client – 2 - (Plot 450, Venkateswara English Medium School, Chandrasekharpur) Reply by Client – 3 - (Bhubaneswar Odisha-751016) |
Hariom Patra,class-10, BG-AB+, Plot 450, Venkateswara English Medium School, Chandrasekharpur Bhubaneswar Odisha-751016 |
SM= .625, PC = 100% |
The expected complete student information was provided. |
|
2 |
Sumbit Singh, Roll-34 Unit-4 Boys High School Unit-4 PlotNo-56 Bhubaneswar |
Reply by Client – 1 – i)Sumbit Singh,class-7 roll-49,BG-0+ Reply by Client – 2– Unit-4 Boys High School PlotNo-56,Unit-4 Reply by Client – 3 – Bhubaneswar,Odisha-751003 Reply by Client – 1 – ii)Sumit Singh,class-7 roll-34,BG-0+ Reply by Client – 2 – Unit-4 Boys High School PlotNo-56,Unit-4 Reply by Client – 3 – Bhubaneswar,Odisha-751003 |
i) Sumbit Singh,class-7 roll-49,BG-0+ Unit-4 Boys High School PlotNo-56,Unit-4 Bhubaneswar,Odisha-751003 ii) Sumit Singh,class-7 roll-34,BG-0+ Unit-4 Boys High School PlotNo-56,Unit-4 Bhubaneswar,Odisha-751003 |
SM = .566 PC = 51 SM = .542 PC = 49 |
Here in the input student information is wrongly spelled.
|
-
B. Student Identification based on the Student Object (Parallel Mapping) with the knowledge Base
The experiment that we have conducted is very encouraging as is depicted in the below mentioned Table: 6 and Figure 7 where it shows, the running time of the proposed model can be reduced drastically by implementing a parallel model of the proposed system.
For conducting the experiment, we have used 3 client systems with P4 processor and one server with core i3 processor connected with peer to peer network. In the first instance we have used 10K records where the running time of sequential and parallel execution of the algorithm as 28125 ms and 14969 ms, which suggests that the running time have been reduced to it’s half by having a parallel model for the proposed system. Similar trends have been shown in the below table with varying degree of records.
We could cut down the running time of the proposed model to its half with 20K records i.e. in sequential and parallel execution as 57950 ms and 29975ms. With 30K records the running time of sequential and parallel execution shows as 81416ms and 44708ms and so on.
Table 6. Student Component Information Structure
|
Experiments |
No of Records |
Time taken in Sequential Execution in Milliseconds |
Time taken in Parallel Execution in Milliseconds |
|
Experiment - 1 |
10000 |
28125 |
14969 |
|
Experiment - 2 |
20000 |
57950 |
29975 |
|
Experiment - 3 |
30000 |
81416 |
44708 |
|
Experiment - 4 |
40000 |
116060 |
63030 |
|
Experiment - 5 |
50000 |
151081 |
78909 |
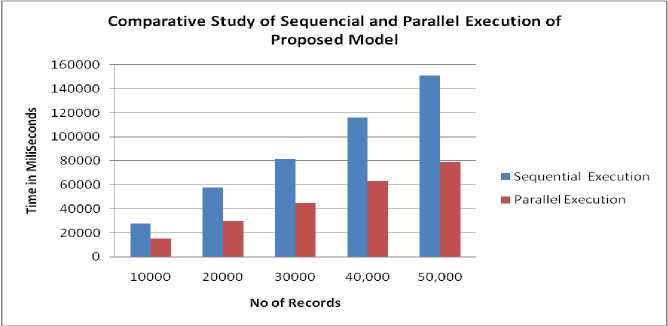
Fig.7. Comparative study of sequential and parallel execution of proposed model.
-
VIII. Conclusion
The parallel soft computing model employed in this paper addresses one of the vital tasks of identifying a lost student with minimal information. It uses symbolic similarity measures for student object generation based on the input student details and parallel student object mapping. These likeness measures are considered as a fuzzy membership functions. Then we have to de-fuzzify the output by applying alpha cut technique. We have done a comparative study of our earlier work with the proposed parallel model and found that our proposed model is faster twice than the earlier work i.e. our proposed parallel model takes half of the time taken by the earlier single thread model.
Список литературы A parallel soft computing model for identifying lost student in an incomplete and imprecise environment
- F. Sebastiani, Machine learning in automated text categorization. ACM ComputingSurveys, 34(1), pp. 1–47, 2002.
- Y. Yang, and J. Pedersen, “A comparative study on feature selection in text categorization” In International Conference on Machine Learning (ICML), 1997.
- S. Fabrizio, Machine learning in automated text categorization, ACM Computing Surveys 34 (1) pp. 1–47, 2002.
- H.-H. Bock, E. Diday, Analysis of Symbolic Data, Springer, Heidelberg, 2000.
- E. Diday, Knowledge discovery from the symbolic data and the SODAS software, in: PKDD 2000, Workshop on Symbolic Data Analysis, Lyon, 12th September 2000.
- Lecture notes of short term course on symbolic and fuzzy approaches to data analysis, 21–26 April 1997.
- K. Chidanada Gowda, “Symbolic objects and symbolic classification”, Proceedings of International Conference on Symbolic and Spatial Data Analysis: Mining Complex Data Structures Pisa, pp. 1–18, 20 September, 2004.
- Y. El-Sonbaty and M.A. Ismail, Fuzzy clustering for symbolic data, Fuzzy Systems, IEEE Transactions in, Volume: 6, pp .195 - 204, on May 1998
- D.H. Hung and S.Y. Hwang, A note on the value similarity of fuzzy systems variables, Fuzzy Sets and Systems 66 (1994) pp.383-386.
- C.P. Pappis and N.I. Karacapilidis, A comparative assessment of measures of similarity of fuzzy values, Fuzzy Sets and Systems 56 pp. 171-174,199
- S.R.Dash, S Rayaguru, S.Dehuri, Sung-Bae Cho “Lost Student Tracking in an Incomplete and Imprecise Information Environment Using Soft Computing Paradigm”, International Journal of Artificial Life Research, volume 3, Issue 4,3(4), 32-48, October-December 2012
- P. Nagabhushan a, S.A. Angadi b, B.S. Anami c, “A soft computing model for mapping incomplete/approximate posstal addresses to mail delivery points”, Applied Soft Computing, volume- 9, Issue – 2 , pages- 806–816, March – 2009
- P. Nagabhushan a, S.A. Angadi b, B.S. Anami c, “A Fuzzy Symbolic Inference System for Postal Address Component Extraction and Labelling”, FSKD, volume – 4223 of Lecture Notes in Computer Science, page 937 –946, September 24-28 2006.
- Mahendra Kumar Gourisaria, BSP Mishra, S Dehuri “A Hybrid Parallel Multi - objective Genetic Algorithm: HybJaclsCone Model, in International Journal of Computer Application, Volume 66 No. 7, March 2013.
- Samira Chouraqui, Boumediene Salema, “Unmanned Vehicle Trajectory Tracking by Neural Networks, The International Arab Journal of Information Technology, Volume 13 No. 6B, 2016
- Magdalen Diering, Krzysztof Dyczkowski, Adam Hamrol, “New Method for Assessment o f Raters Agreement Based on Fuzzy Similarity, 10th International Conference on soft Computing Models in Industrial and Environmental Applications, Springer, AISC, volume – 368, June 2015


